基于人工蜂群算法的电力系统网络安全风险评估模型
徐佳,贺渝镔,李润玲
(1.中国南方电网云南电网昆明供电局,云南 昆明 650000;2.昆明东电科技有限公司网络空间安全事业部,云南 昆明 650000)
0 前言
随着计算机与网络技术的快速发展与普及,数据采集系统(Supervisory Control and Data Acquisition,SCADA)等工业控制设备逐渐被引入到电力系统的日常生产中[1-3]。近年来,在广泛应用IP 协议的背景下,电力SCADA 系统遭受大量的攻击,造成了较多无法挽回的经济损失。因此如何对其网络运行状态进行精确的安全评估,成为了电力系统设计者亟需解决的重要问题。针对这一问题的研究,国内外学者曾给出了一些具有借鉴意义的解决方法[4-7],即利用风险评估模型进行必要的分析与预测。例如,文献[8]提出使用折中图或漏洞树的方法,从概率的角度评估系统受攻击的可能性。然而该方法的评估过程存在较大的主观因素,难以得到客观中立的评估结果;文献[9]通过引入专业数据库、风险模板与风险分析技术,提供了定性与定量分析电力系统的自动工具。但该种工具的评估过程复杂度较高,其应用范围具有一定的局限性。
针对电力系统的网络安全风险评估问题,文中详细介绍与分析了高斯过程的主要原理。利用人工蜂群算法对高斯过程的超参数进行最大程度的优化与改进,从而提出网络安全风险评估模型的执行流程及实现方法。基于Matlab软件,文中利用大量的测试数据对该模型进行必要的仿真与测试。相应结果表明,与遗传算法相比,基于人工蜂群算法的评估模型具有更低的时间复杂度和更高的评估精度。
1 高斯过程
从广义角度上,高斯过程(Gaussian Process)可被视为一种基于贝叶斯分析思想的机器学习方法。从数学角度上,高斯过程是一种随机过程,由多个服从高斯分布的随机变量组合而成。由于具有较少的参数,且其超参数可由自适应函数获取,所以高斯过程被应用于网络安全的风险评估模型中,其详细介绍如下[10-11]。
1.1 定义
假设存在训练样本集合R=(x,y),其中x=(x1,…,xn)是包含n项数据的输入向量,且任意第i个分量xi均服从高斯分布,y是高斯过程的输出值。此外,令g(x)表示训练样本输入数据的函数,δ表示系统噪声,服从高斯分布,即。则输出y与输入x之间存在以下的关系,如式(1)所示。

设高斯过程的均值函数是m(x),协方差函数为c(x,x'),令E表示期望函数,则这两者的基本定义,如下式所示:

利用均值与协方差函数,文中即可给出高斯过程的准确定义,如式(4)所示:
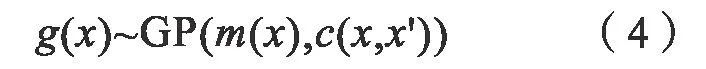
在具体的计算过程中,均值函数通常被设置为0,协方差函数直接影响高斯过程的预测与评估结果。因此文中选取了无限可微的高斯核函数,作为高斯过程的协方差函数,其具体形式如下。
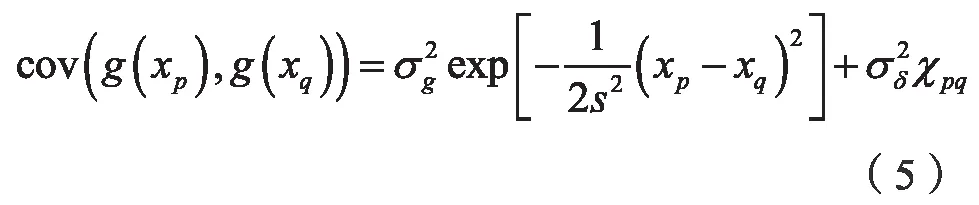
其中,xp与xq分别表示两项不同的输入数据,σg与σδ分别表示函数g(x)和噪声δ的标准差,s表示高斯过程中的R维关联超参数,其数值越大,输入与输出之间的相关性则越小。χpq表示Kronecker 符号,若p=q,则χpq=1;否则,χpq=0。通常在高斯过程中,函数g(x)的标准差σg、噪声δ的标准差σδ以及衡量输入和输出之间相关性的关联超参数s,被统称为高斯过程的超参数,即θ=(s,σg,σδ),其维度为R+2。
1.2 训练与预测
为实现精准的预测,高斯过程需要进行一定数量的训练。在此过程中,由于噪声δ与函数g是相互独立的高斯分布变量,所以输出y也服从高斯分布,如式(6)所示。
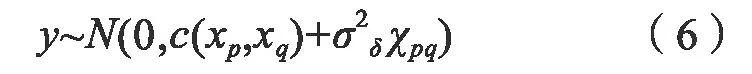
其中,c(xp,xq)表示输入xp与xq的协方差函数,σδ表示噪声标准差,而χpq表示Kronecker符号。此时,设测试样本数据为Rtest=(xtest,ftest),则观察值yo与测试输出值ftest的联合先验分布,如式(7)所示。

其中,C(x,xtest)、C(xtest,x)和C(xtest,xtest)均为n×n维的协方差矩阵,负责评估训练数据x与测试数据xtest之间的相关性。利用式(6)、式(7)可得到高斯过程的预测方程与目标方程,分别如下式所示。
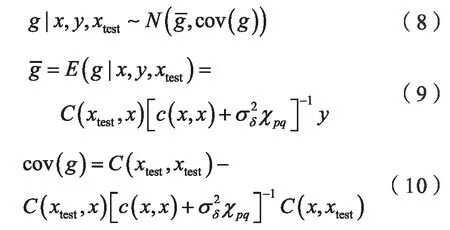
1.3 优化原理
为了尽量优化高斯过程的目标函数,文中随机选取超参数的初始值,再根据相应的预测结果,利用人工蜂群算法对超参数进行调整与优化,从而得到具有精准预测能力的目标函数。在此过程中,对于训练数据R=(x,y),其似然概率分布p(y|x)的公式,如式(11)所示。

其中,函数g与输出y的先验概率分布均服从高斯分布,即g|x~N(0,σ2),y|g~N(g,σ2gχ)。超参数的边缘似然函数logp(y|x),如式(12)所示。

2 人工蜂群算法
2005 年,针对多变量函数的优化问题,Karaboga 研究小组通过观察蜜蜂的行为,提出了群体的智能优化算法,即人工蜂群算法。其主要原理是利用多个体的局部寻优动作,获取全局的最优解。这种算法具有较少的控制参数、较快的收敛速度与较强的稳定性等多种优点[12-13],所以文中引入人工蜂群算法对基于高斯过程的风险评估模型进行优化。
在算法运行中,不妨设初始蜜源(初始解)XD=(x0,...,xD-1)是D维向量,且D=R+2。引入S个雇佣蜂,开采蜜源的最大次数为tL,算法最大循环次数为MAX,f表示蜜源的适应度函数,其数学表达式,如式(13)所示。

若适应度函数的绝对值越小,则蜜源的质量越高。利用以上这些条件,人工蜂群算法的执行步骤如下。
1)雇佣蜂搜索与记录蜜源信息,并将这些信息传送至等候的观察蜂;
2)在收到的信息中,观察蜂以一定的概率选择当前解,并搜索其附近的局部解。若局部解优于当前解,则局部解替代当前解。其中,令pi表示第i个蜜源的概率结果,则观察蜂的概率计算公式,如式(14)所示。

而利用原蜜源X、原蜜源的邻近解X'以及处于[-1,1]之间的随机数φ,可以得到新蜜源V的生成方法,如式(15)所示。

3)若算法的开采次数超过MAX,则放弃当前解。然后将雇佣蜂转化为侦查蜂,按照式(14)的方法,侦查蜂在原蜜源X附近继续随机搜索新蜜源。
3 风险评估模型
在电力系统中,高斯过程通常被用于网络安全的风险评估模型中,其超参数的优化程度较大地影响了模型的评估精度。通常而言,共轭梯度法常被用来对超参数进行优化。然而该种算法容易陷入局部反复循环,从而难以获取全局最优解。为了避免这一缺点,本文引入具有全局搜索能力的人工蜂群算法对超参数进行优化,从而大幅提高评估模型的精准度,该模型的实现步骤如下。
1)初始化
在模型的初始化阶段,随机生成初始蜜源Xi=(Si,σgi,σδi,)(i=0,...,S-1),开采蜜源的最大数量为tL=S×D,令开采次数item=0,外层循环的最大次数设置为MAX,记录循环次数为I=1;
2)计算适应度函数
利用初始化后的多项参数,以及作为蜜源的超参数,建立基于高斯过程的评估模型,从而输出优化后的目标值。然后,再使用式(13)计算该蜜源的适应度值,从而评估出该超参数的质量。
3)雇佣蜂
利用当前蜜源与式(15)随机生成新蜜源,基于高斯过程模型的各项参数计算该蜜源的适应度函数值。若新蜜源的适应度优于当前蜜源,则令新蜜源代替当前蜜源继续执行算法;否则,保留当前蜜源。此外,在跳舞阶段,雇佣蜂将蜜源信息转达至观察蜂。
4)观察蜂
在这一阶段,观察蜂利用获取的蜜源信息,通过概率计算式(14)对当前蜜源的邻近蜜源进行充分的开采。然后采用式(13)随机生成新蜜源,同时对比当前蜜源与新蜜源的适应度函数值,从而保存质量较优的蜜源信息。
5)更新开采次数
若在步骤4)中选择新蜜源作为当前蜜源信息,则令开采次数item=0;否则,开采次数item=item+1。
6)侦查蜂与条件判断
经过多次的开采,当前蜜源的邻近蜜源信息接近耗尽,即蜜源质量难以提高。当蜜源开采次数item<tL时,若循环次数I≥MAX,则结束整个人工蜂群算法,并输出最终超参数值;若I<MAX,则继续开采蜜源信息。当蜜源开采次数 item≥tL,则随机生成新蜜源,重置开采次数item,同时抛弃当前蜜源,跳转至步骤(2);
7)建立模型
利用优化后的超参数与训练数据,在高斯过程的基础上形成网络安全的风险评估模型。
为了建立精准的风险评估模型,上述多个步骤需要在一定的条件下重复运行,所以需要制定相应的流程对这些步骤进行精准的控制。该模型的具体流程,如图1 所示。

图1 网络安全风险评估模型流程
4 仿真测试与分析
为了验证本文提出模型的有效性,在同样的初始值和输入等仿真条件下,利用Matlab r2016a 软件,文中分别基于遗传算法(Genetic Algorithm)与基于人工蜂群算法的风险评估模型进行多次仿真与实验,并统计这两种模型的时间复杂度和评估准确度。
为了客观地评估模型的时间复杂度与评估准确度,文中在这两种模型的算法程序中,设置了相同的基本参数。具体情况,如表1 所示。

表1 模型仿真程序参数设计
在仿真过程中,ABC 表示基于人工蜂群算法的评估模型,GA 表示基于遗传算法的评估模型。此外,文中分别选取了150 项训练数据与70 项的测试数据,从时间复杂度与评估精确度角度对这两种模型进行反复的实验与对比。需要说明的是,本文使用了适应度函数衡量模型的评估准确度,而时间复杂度由所耗费时间进行衡量。其具体统计结果,如图2、图3 所示。

图2 两种评估模型的时间复杂度统计结果

图3 两种评估模型的评估精确度统计结果
在图2 中,横轴表示评估模型的运行次数,纵轴表示模型所耗时间,单位为s。虚线与实线分别记录了基于遗传算法和人工蜂群算法的评估模型,在不同评估次数时所耗时间。由曲线的走势可知,在评估次数<5000 时,人工蜂群算法所耗时间略小于遗传算法。而当评估次数不断增加,人工蜂群算法所耗时间明显小于遗传算法。这说明,基于人工蜂群算法的评估模型的时间复杂度更低。
与图2 类似,在图3 中横轴表示评估模型的运行次数,纵轴表示模型最终解的适应度函数值,虚线表示基于遗传算法的评估模型,实线表示本文所提出的模型。由图3 可知,在初始解相同的情况下,当两种模型的运行次数相同时,文中所提模型得出的最优超参数的适应度函数值严格小于基于遗传算法的评估模型,这表明本文评估模型的评估准确度更高。
综上所述,与经典的遗传算法模型相比,基于人工蜂群算法的网络安全风险评估模型,具有更低的时间复杂度与更高的评估准确度。
5 结束语
本文综合人工蜂群算法与高斯过程的相关理论,提出了适用于电力系统、且具有较低时间复杂度与较高评估精度的网络安全评估模型,Matlab 软件的仿真结果直接证明了该模型的有效性与优越性。然而由于尚未在电力系统进行测试验证,所以该模型可能仍存在一定的缺陷与不足。例如,该模型的鲁棒性表现仍缺乏测试环境和条件限制。在未来的工作中,将致力于实际工程测试、完善与推广该模型的算法设计。

