喷水减温阀离心喷嘴雾化性能的优化研究
孙泽刚, 胡自强, 何德文, 吴笑天
(四川轻化工大学 机械工程学院, 四川 自贡 643000)
引言
离心式喷嘴是喷水减温阀的重要零件,具有结构简单,运行可靠的优点。在温度调节部件中,减温水通过喷嘴形成雾化液滴,进入温度调节部件的流道后与高温蒸汽接触,吸收热量迅速汽化,以达到降低蒸汽温度的目的[1]。喷嘴的结构和形状直接影响雾化性能的好坏,不合理的结构参数选择会影响减温过程的效率。
近年来国内外学者主要采用数值模拟和实验分析两种方法。陈晓东等[2]通过VOF方法研究了不同背压下离心喷嘴内液膜厚度,研究表明随气体密度增加而减小的气液界面附近过渡区域中的平均速度分布是导致液膜厚度增加的原因;邱庆刚等[3]用VOF方法分析了离心喷嘴出口结构参数对液膜厚度的影响规律;杨立军等[4]模拟比较了喷嘴出口直管段长度对液膜厚度的影响;莫妲等[5]通过实验研究不同压力工况旋流槽长宽比和旋流槽角度对雾化性能的影响;刘赵淼等[6]采用实验的方法研究了压力和旋流槽数量对液膜破碎和雾化性能的影响;FERREIRA等[7]通过试验探究了影响其喷射效果的设计参数。
上述研究大多采用单因素实验的方法,该方法实验次数较多,只能确定各参数与指标之间的关系,没有考虑参数之间的交互作用对喷嘴的影响。因此,本研究运用数值模拟的手段,探究喷嘴的出口直径、旋流室角度和旋流槽角度这3个因素及其交互作用对喷嘴雾化效果的影响,用响应面法建立雾化锥角和流量系数的代理模型,并使用粒子群算法,得到最优喷嘴结构参数,提高雾化性能。此研究旨在通过对喷嘴结构的优化,提高喷嘴雾化性能,进而提高喷水减温阀的减温效果。
1 喷嘴的结构模型
本研究的离心喷嘴是一种单通道喷嘴,喷嘴的结构如图1所示,整个喷嘴主要由喷头、旋流片和壳体组成。减温水通过喷嘴入口到达旋流片区域,由于内部湍流的作用,减温水将旋转并被甩动到旋流槽的槽面上,惯性力克服表面张力继续向外扩张,在喷嘴出口区,使液膜失稳破碎为丝状或带状[8]。当有外界作用力时,随着液膜变薄,表面势能越来越高,液膜与空气相对运动剧烈,表面张力被破坏,破碎为小液滴[9],然后从喷口高速喷出,形成喷雾。
2 数值模拟方法
本研究采用Fluent软件,在数值计算中用VOF方法模拟离心喷嘴内外场的流动过程,HIRT等[10]最先提出VOF方法,该方法可以用于不可压缩、不混合流体的计算。VOF方法在计算时定义体积分数α来表征流体在计算网格内的分布。通常将密度小的空气定义为第一相,水定义为第二相。若α=0,网格内全部是空气;若α=1,网格内都是水;若0<α<1,则网格内部分是水,部分是空气。流体按不可压处理,VOF 模型控制方程如下:
连续方程:
(1)
式中,ρ—— 流体密度
u—— 时均速度
动量方程为:
(2)
式中,μ—— 动力黏性系数
p—— 流体压力
采用Realizablek-ε作为湍流模型,k和ε方程为:
(3)
式中,k—— 湍动能
ε—— 湍动耗散率
Gk—— 由于平均速度梯度引起的湍动能k的产生项
σk,σε—— 分别为k和ε的湍流Prandtl数
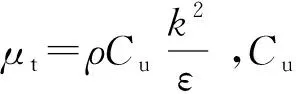
(4)
式中,E—— 平均应变率
v—— 运动黏度
C1,C2—— 常数
模型网格划分和计算域如图2所示,为了保证计算结果和网格数量无关,对喷嘴不同数量的网格进行数值模拟,如表1所示,可以看出65万网格可以较好的模拟出喷嘴的雾化特性,其雾化锥角的误差不超过2.92%,再增加网格只会降低计算速度,因此采用65万网格的模型进行模拟分析。
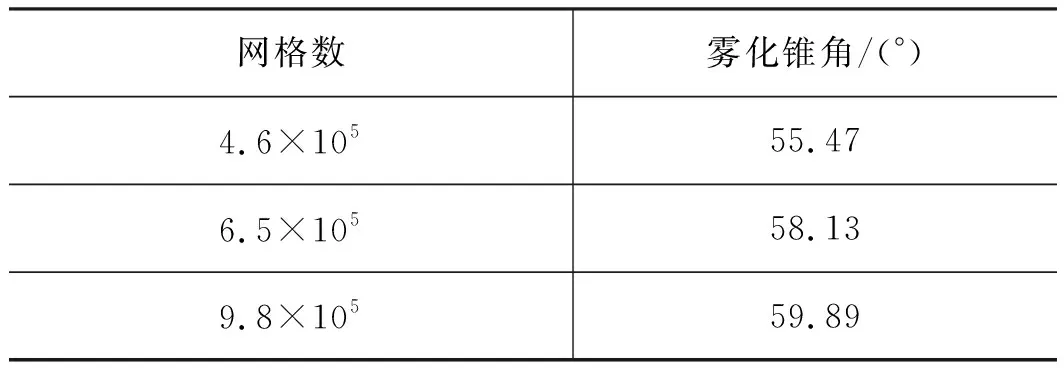
表1 网格数对计算结果的影响Tab.1 Influence of grid number on calculation results
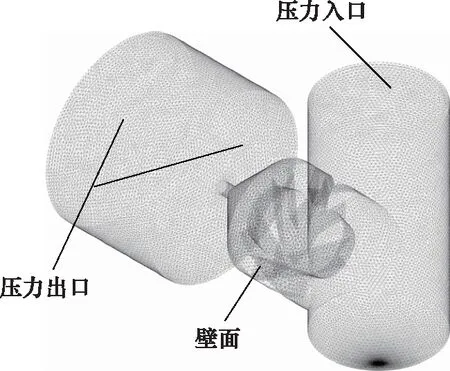
图2 计算区域及网格图Fig.2 Calculation area and grid diagram
两相相互作用模型选择表面张力模型,设定空气和水之间的张力系数为0.072 N/m。采用SIMPLE算法进行计算。压力相的离散格式选用PRESTO。进口采用压力进口,压力为1 MPa,进口处水的体积分数为1。出口采用压力出口,压力为大气压,出口处水的回流系数为0,表示出口处只存在空气回流。壁面为无滑移壁面。计算初始时间步长为10-8,最大时间步长为10-5,对喷嘴进出口流量进行监视,当进出口流量差值小于1%时,判定计算结果已收敛。
3 优化方法
3.1 正交实验设计
正交实验设计是多因素多水平试验的优化设计方法,主要是用正交表进行方案设计,可以根据因素数和水平数的交互作用选择正交表,实现用最少的实验次数获得高效的实验结果。
3.2 响应面代理模型
响应面代理模型是用回归方程拟合输入参数和输出参数函数关系的一种代理模型,通过构建回归方程能将复杂的模型关系表示出来[11]。同时通过方程的各个系数可以看出代理模型,通过构建回归方程能将复杂的模型关系表示出来,且在求解最优值问题中,优化过程简单。而二阶响应面模型有比较高的精确度,需要的样本点数最少为(n+1)(n+2)/2,表达式为[12]:
(5)
其中,xi是第i个设计变量,y对应评价指标,a0,bij,cij,dij为代理模型多项式的系数。为了判断拟合的代理模型能否准确表达离心喷嘴的响应关系,需要进行精度检验,用R2来决定。R2的表达式为:
(6)
式中,ST—— 总偏差平方和
SR—— 回归平方和
SE—— 残差平方和
R2越接近1,说明模型的精度越高,当R2大于0.9时,认为该模型的精度可达到要求。
3.3 粒子群算法
粒子群算法属于群智能优化算法的一种,算法中每个粒子代表1个问题的可能解。粒子的飞行过程是该个体的搜索过程,通过对粒子的速度和位置的不断更新,从而实现个体在空间中的寻优[13]。公式为:
vi(t+1)=ωvi(t)+c1r1(Pbesti(t)-xi(t))+
c2r2(Gbesti(t)-xi(t))
(7)
xi(t+1)=xi(t)+vi(t+1)
(8)
其中,c1,c2为学习因子,通常取[0,2];ω为惯性权重,通过调整其大小,调整算法的寻优性能,r1,r2为加速度权重系数,取[0,1]上的随机数[14]。通过上述两式实现对粒子的速度和位置的更新。当迭代次数达到最大次数,停止迭代,输出最优解。
4 结果及分析
本研究取3个因素,每个因素4个水平,其中A为出口孔径,B为旋流槽角度,C为旋流室角度,结合喷嘴实际的设计情况,确定变量范围,如表2所示。
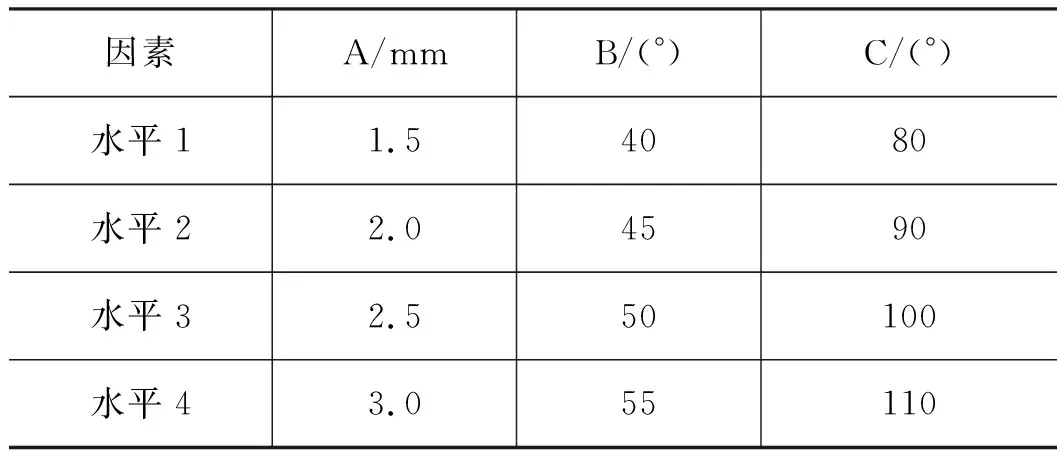
表2 正交实验设计因子水平表Tab.2 Factor level of orthogonal experimental design
根据表2进行正交实验设计,合理安排得到16组不同结构参数的喷嘴,如表3所示,对其进行数值模拟,得到雾化锥角θ和流量系数Q的结果。
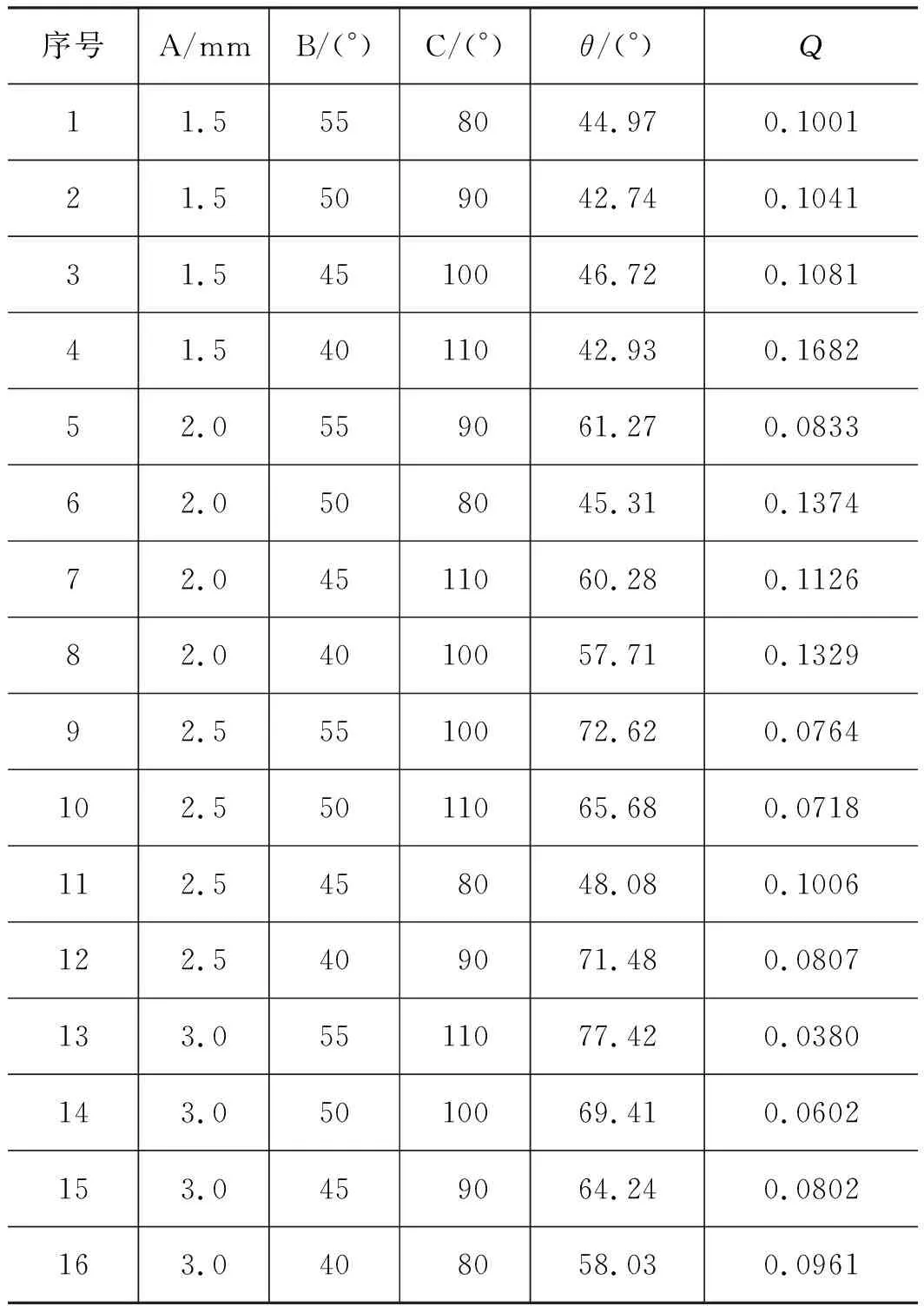
表3 正交组合设计及实验结果Tab.3 Orthogonal combination design and experimental results
以6号喷嘴为例说明离心式喷嘴的流动特性。从图3、图4可以看出水流进入旋流室后,边缘处速度最低,越靠近中心处速度越大;压力则是边缘最大,越靠近真心处压力越小。

图3 旋流室速度矢量图Fig.3 Velocity vector diagram of swirl chamber
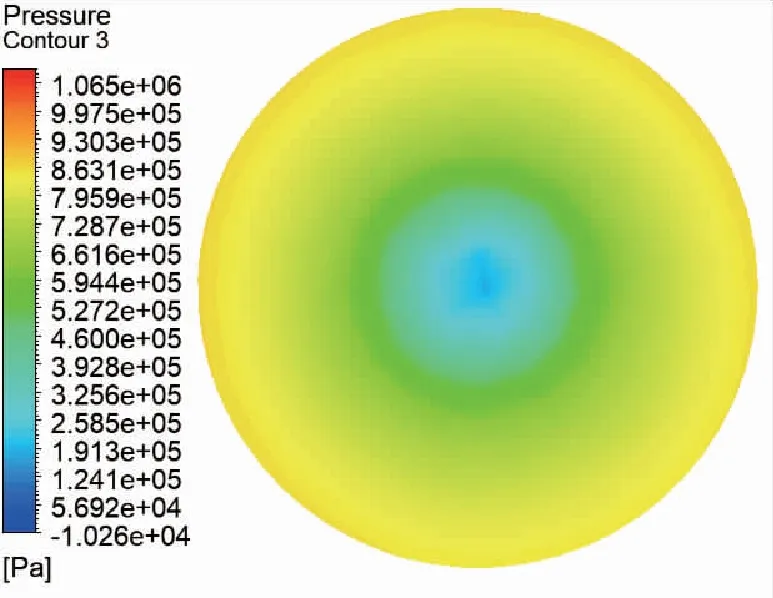
图4 旋流室压力云图Fig.4 Pressure cloud diagram of swirl chamber
从图5、图6可知,在喷嘴出口处产生负压 ,由于在出口处压力减小,水流速度增大,因为外界压强比喷口部分高 ,空气被吸入喷口,在出口处形成回流区。
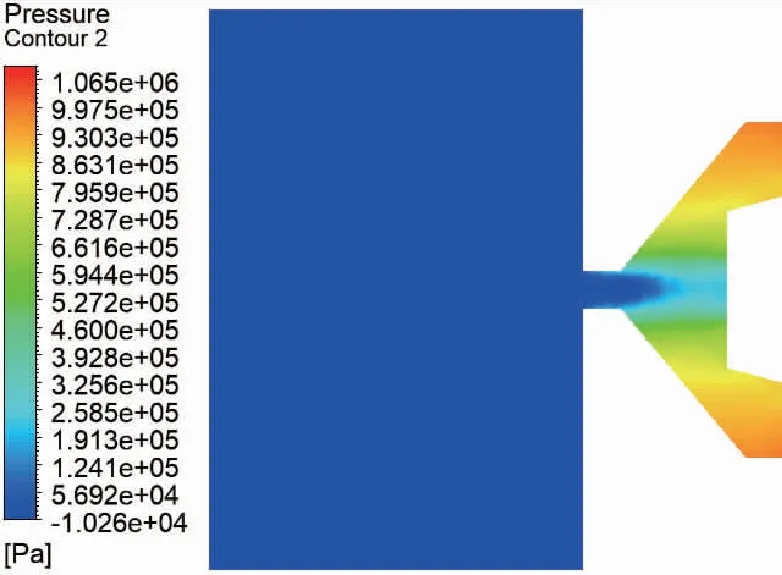
图5 z=0处截面压力云图Fig.5 Pressure nephogram of section at z=0
4.1 方差分析
表4、表5利用F函数对因素进行方差分析[15]:
Fα(n1,n2)=F
其中,n1为各因素、各因素之间的交互作用对应的自由度,n2为误差自由度之和;查表得F0.05(2,12)=3.89,当F>F0.05时,表明该因素对指标影响显著,Ki表示某因素第i个水平的实验均值[8]。

图6 z=0处速度矢量图Fig.6 Velocity vector diagram at z=0
表4表明:方差值FA>F0.05,出口直径对雾化锥角的影响最显著;K4A>K3A>K2A>K1A,K4B>K1B>K3B>K2B,K3C>K2C>K4C>K1C,雾化锥角随出口直径、旋流槽角度、旋流室角度呈增大趋势。
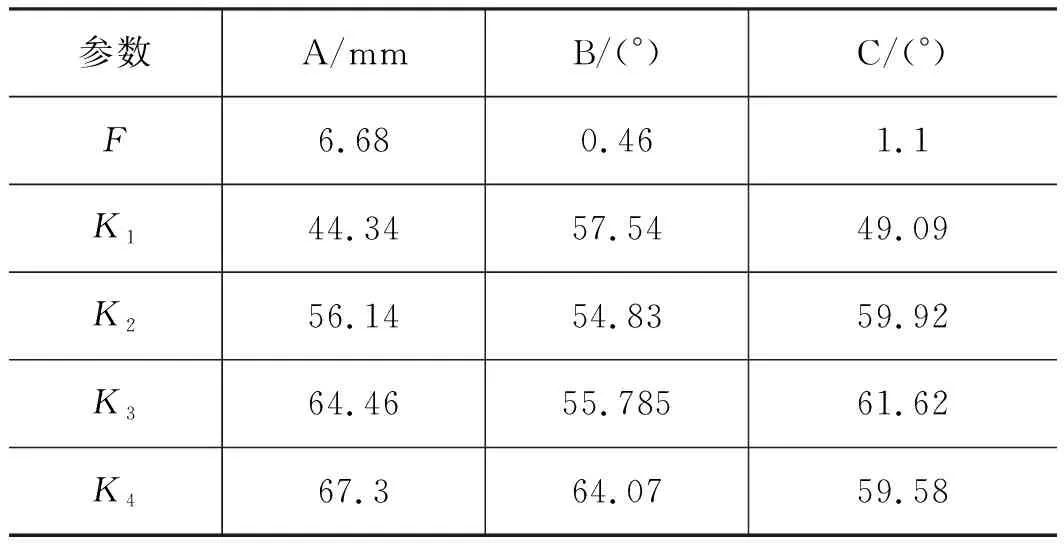
表4 雾化锥角方差分析Tab.4 Analysis of variance of spray angle
表5表明:方差值FA>F0.05,出口直径对流量系数的影响最显著;K1A>K2A>K3A>K4A,K1B>K2B>K3B>K4B,K1C>K4C>K3C>K2C,流量系数随出口直径、旋流槽角度、旋流室角度呈减小趋势。
4.2 回归分析
为了反映出喷嘴结构参数对雾化锥角、流量系数的影响规律和趋势,对表4和表5中的指标与各因素之间的关系进行拟合,得到规律曲线。其中,雾化锥角和喷嘴出口直径的关系采用二次拟合,拟合方程如式(9);流量系数和喷嘴出口直径间的关系采用二次拟合,拟合方程如式(10);其他结构参数和评价指标之间的关系采用保形拟合[8]:
y=-8.9925x2+55.892x-19.366
(9)
y=-0.0102x2+0.0081x+0.1335
(10)
图7中3条曲线可以表明:出口直径对雾化锥角的影响最显著,其次是旋流室角度,影响最小的是旋流槽角度。其中,随出口直径的增大,雾化锥角呈现增大的趋势;随着旋流槽角度的增大,雾化锥角也呈现增大的趋势;随着旋流室角度的增大,雾化锥角呈现先增大后减小的趋势。
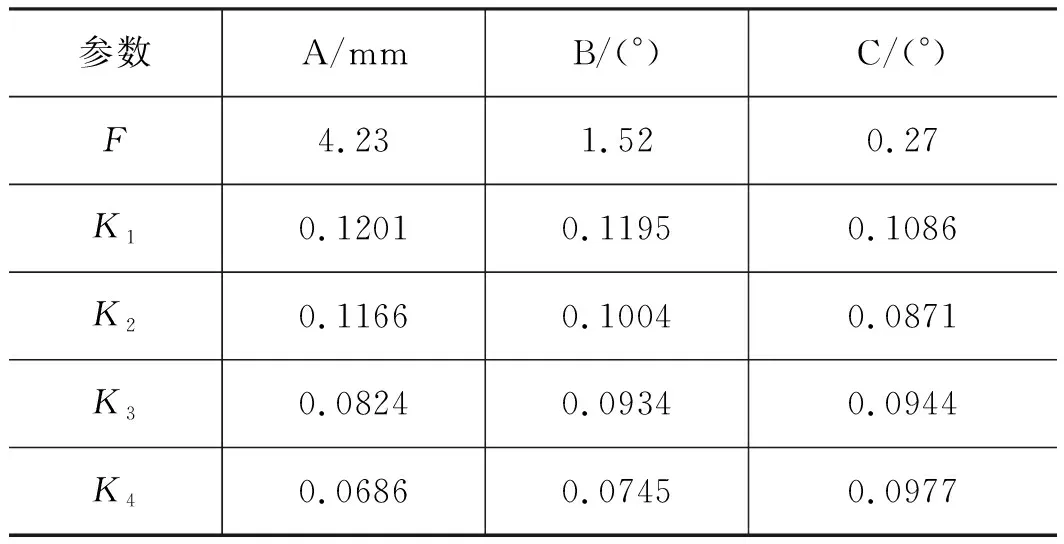
表5 流量系数方差分析Tab.5 Analysis of variance of flow coefficient
图8中3条曲线可以表明:出口直径对流量系数的影响最显著,其次是旋流槽角度,影响最小的是旋流室角度。其中,流量系数随着出口直径和旋流槽角度的增大而减小,随着旋流室角度的增大先减小后增大。
4.3 建立响应面代理模型
根据3.2节的阐述,进行响应面函数拟合,其表达式为:
0.347x1x3+0.0095x2x3
(11)
yQ=0.041-0.005x1+0.0083x2-6.4×10-4x3-
0.00349x1x2-0.001425x1x3-1.88×10-4x2x3
(12)
经计算后可得,雾化锥角yθ方程的回归系数R2=0.967,流量系数yQ方程的回归系数R2=0.923,说明方程的拟合精度较高,因此可以用此响应面代理模型拟合,简化计算过程。
本研究将雾化锥角和流量系数都达到最大作为最佳雾化效果,数学模型为:
(13)
式中,yθ—— 雾化锥角
yQ—— 流量系数
x1,x2,x3—— 喷嘴出口直径、旋流槽角度和旋流室角度
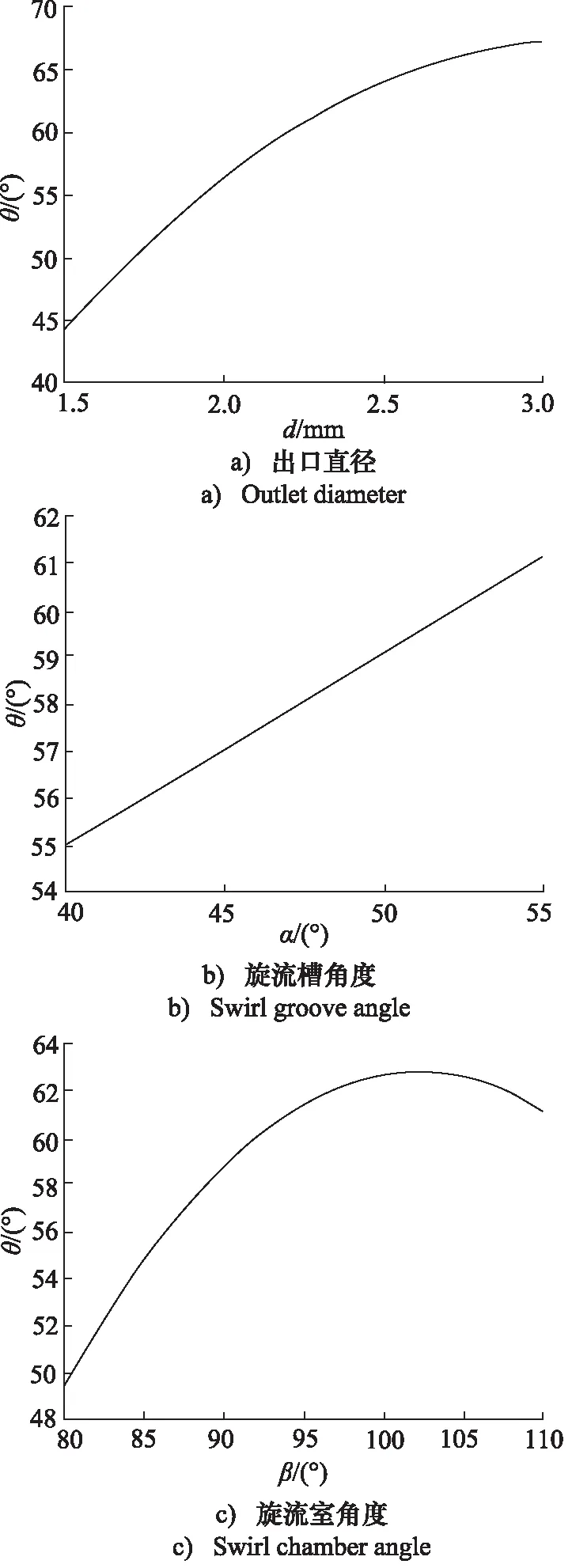
图7 雾化锥角拟合曲线Fig.7 Fitting curve ofatomization cone angle
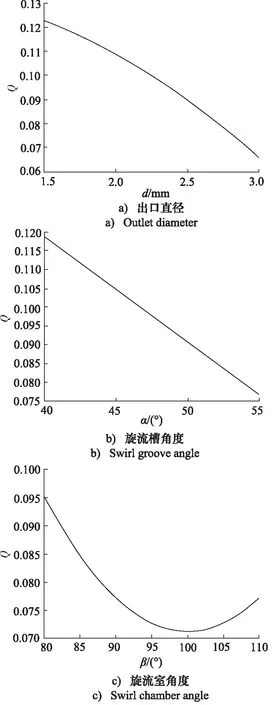
图8 流量系数拟合曲线Fig.8 Fitting curve of flow coefficient
使用加权法对结构参数的取值进行优化,因为雾化锥角θ和流量系数Q对雾化性能的影响同等重要,因此采用权重分别为0.5作为综合指标。对雾化锥角θ和流量系数Q进行归一化处理。计算公式为:
(14)
4.4 优化结果分析
得到响应关系后,用MATLAB编写数学模型,同时设定粒子群算法的运行参数,本研究粒子群体大小取100;最大迭代次数为200次;学习因子采用标准值c1=c2=2,最大权重ωmax=0.9,ωmin=0.4,粒子群算法迭代曲线如图9所示。
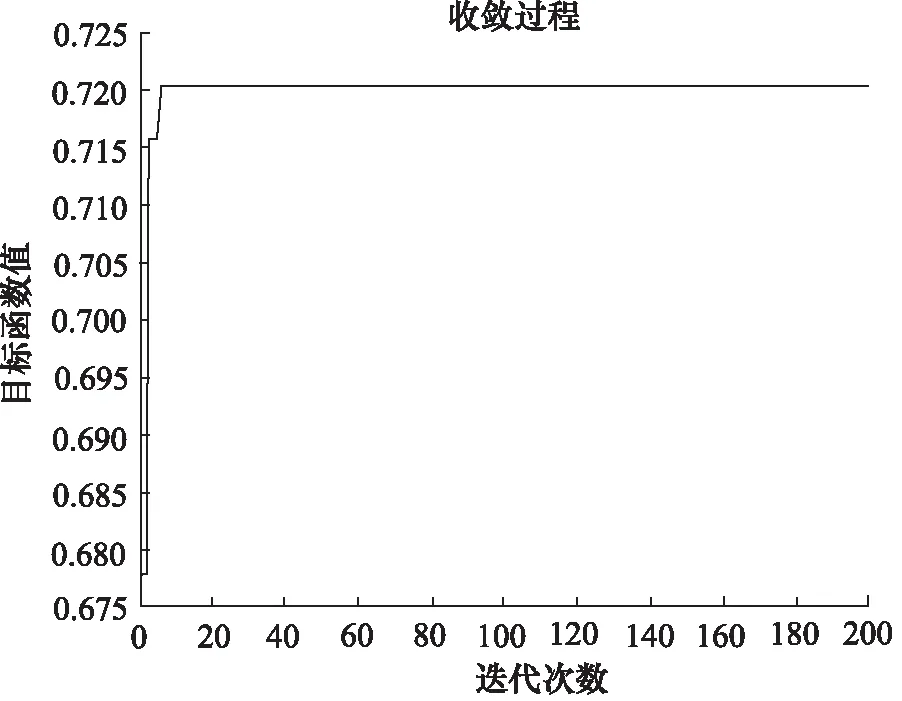
图9 粒子群算法迭代曲线Fig.9 Iterative curve of particle swarm optimization algorithm
优化后喷嘴设计变量的参数如表6所示。

表6 优化后各结构参数Tab.6 Structural parameters after optimization
用粒子群优化得到的各参数对喷嘴进行仿真,得到的仿真结果如表7所示。
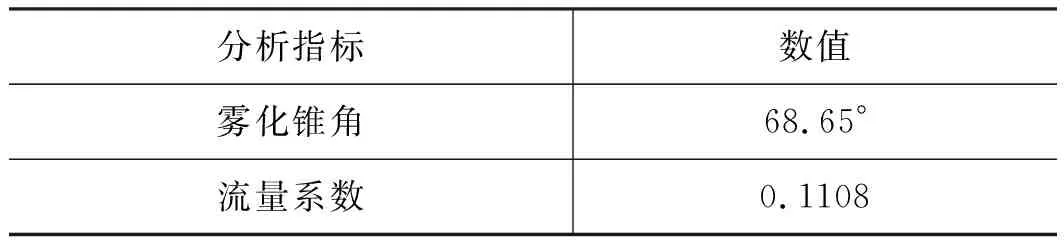
表7 优化后仿真结果Tab.7 Simulation results after optimization
如图10所示,流量系数相对于原模型增大了32.53%;雾化锥角相对于原模型增大了17.7%。使喷嘴在出口附近与空气相互作用更充分,促进减温水的雾化,使减温水与高温蒸汽充分接触,加快汽化速度。
5 结论
在基于VOF方法模拟离心喷嘴的流动,通过正交实验设计的方法研究了喷嘴结构参数对雾化性能的影响得到如下结论:
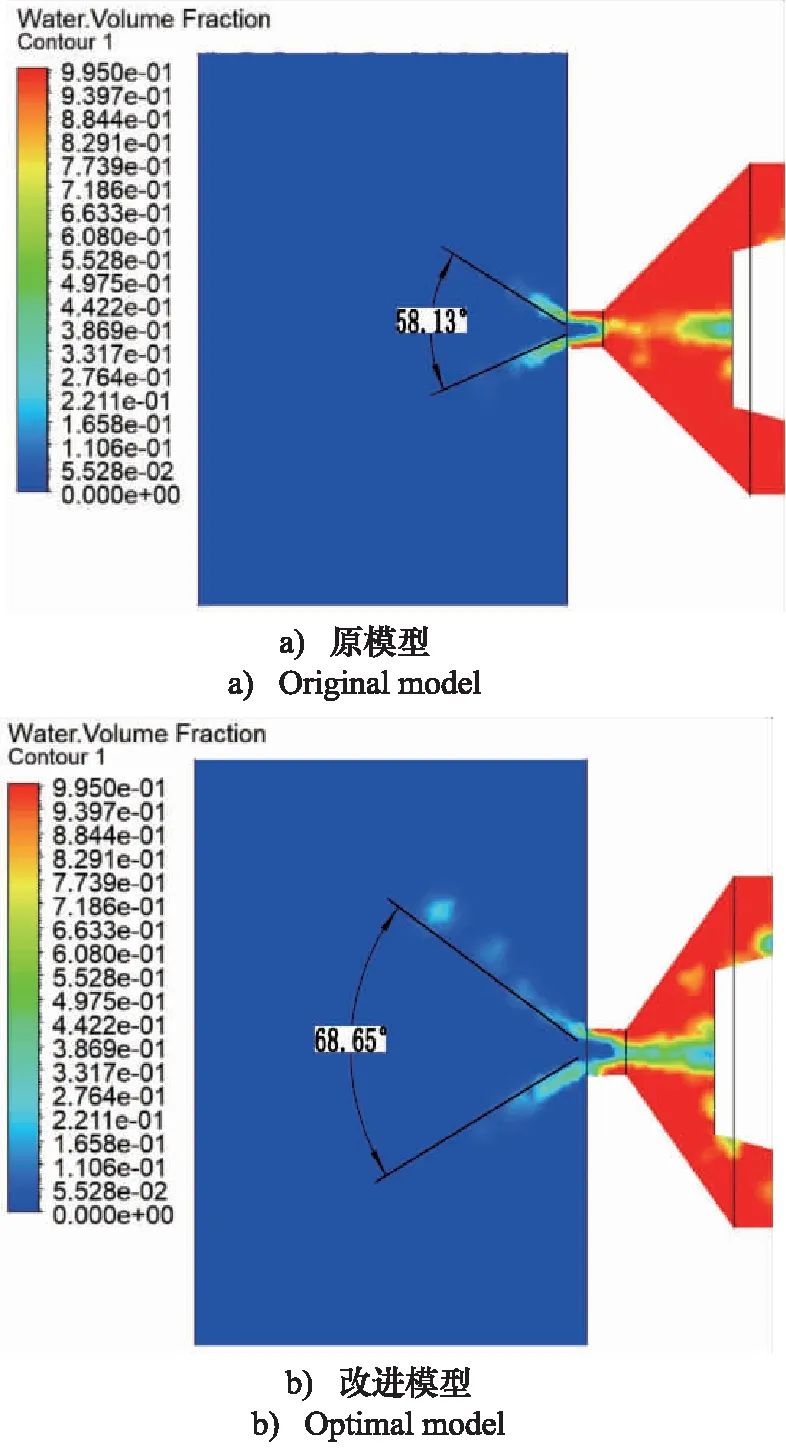
图10 优化前后仿真结果对比Fig.10 Distributions of original model and optimal model
(1) 3个结构参数中喷嘴出口直径对雾化特性的影响最显著,出口直径的增大能显著增大雾化锥角,减小流量系数。旋流槽角度和旋流室角度的增大在一定程度上增大雾化锥角,减小流量系数。
(2) 对喷嘴优化前后的仿真结果进行对比。结果表明,当出口直径为2.55 mm,旋流槽角度为40°,旋流室角度为110°时,雾化锥角比优化前增大17.7%,流量系数增大32.53%,喷嘴的雾化质量得到了改善,为合理选择喷嘴结构参数提供了参考。

