“感觉、感知、感悟”视角下概念教学的再思考*
王小青 (江苏省如皋中学 226500)
1 “感觉、感知、感悟”教学过程的理解
动感:动,合“主动与动态”之意.感,含“感觉、感知与感悟”之蕴.动感数学课堂教学是指在数学课堂教学活动中,教育者有目的地引导学生自觉思维,调动学生自主性和能动性,使学习者主动协调各种感官,通过感受新事物、新概念、新问题,主动获取知识,并在此基础上进行反思,实现自我身心从实践走向思维,实现感性思维与理性思维之合一、感知与感悟之交融的过程[1].
“感觉、感知、感悟”教学观念认为:教学过程由“初步感觉,到体验感知,升华为思考感悟”,突出“创设情境、合作交流、对话展示”.从认识论角度看,即为:创设情境,初步感觉;启迪思考,体验感知;学以致用,思考感悟.
2 “感觉、感知、感悟”教学实录——以《向量的数乘》为例
2.1 初步感觉——在实际情境中从数学的视角发现问题、提出问题
师:甲同学从点O出发向东北方向匀速步行,若经过1 s的位移用向量a表示,那么如何表示在同方向上经过2 s的位移?经过3 s的位移呢?
(学生独立思考,得出结论.)

学生2:(方法2)符号表示,a+a,a+a+a.
学生3:(方法3)符号表示,2a,3a.(类比实数的加法运算a+a+a=3a)
师(追问):3a是何种运算的结果?3a又是什么量?依据刚才研究的问题,你能提出一个类似的问题吗?(如何表示从点O出发向西南方向经过1 s的位移?)能将该问题推广为一般情形吗?接着要继续研究什么问题呢?(给一个实数λ与任意向量a的乘积λa来下定义.)
设计说明学生在前面的学习中已经建构了向量的概念,理解了向量的加法与减法运算法则,那么为何要研究向量的数乘?怎样研究?通过实际情境的创设,一是让学生体会到研究向量数乘的必要性与合理性,期待建构向量数乘的基本概念;二是启发学生联想、类比实数乘法的概念,建构数学模型.
在教学过程中,通过教师追问,学生提出类似的问题;在学生与问题情境、教师与学生、学生与学生的有效互动中,发展学生的数学语言表达能力.
2.2 体验感知:分析问题,建构数学概念
师:联想向量加法的定义,给出一个实数λ与任意一个向量a的乘积λa的定义.
设计说明学生已经建立了研究向量加法、减法运算的定义模型,定义与向量有关运算的思路:(1)确定一个向量,一般从其方向和长度两方面,所以定义要从两个角度入手;(2)对特殊情况的规定(零向量、相反向量);(3)表达数学概念用文字语言、符号语言、图形语言.
(学生独立思考,小组讨论完善,得出结论.)
设计说明数学概念的建构让学生体验感知建构过程,便于学生理解概念并进行数学思考,有数学思考才能解决问题,进一步会产生新的问题,有了新的问题,就会有探究,进一步就会有反思感悟,才能把握数学概念的本质内容,在课堂上要变“结论告知”为“问题思考”,引导学生通过独立思考、合作交流等方式,提升学生的数学能力与素养.
2.3 思考感悟——应用数学,解决数学问题
例1 (1)如果把非零向量a的长度伸长到原来的3.5倍,方向不变得到向量b,向量b该如何表示?
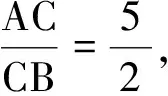
(3)将下列各小题中的向量b表示为实数与向量a的积.

设计说明学生建构向量的数乘等数学模型,应用向量数乘解决这一问题,简化向量运算.在应用过程中,发现运算有一定的规律性,为研究向量数乘的运算律作铺垫.
师:联想实数四则运算律,向量的数乘运算符合哪些运算律呢?(追问)对于①b=2a,也即6e=2(3e)=(2×3)e.这一运算式有怎样的实际意义呢?(再追问)既然向量2(3e)与向量(2×3)e相等,能用图形表示2(3e),(2×3)e吗?
师:你能将上述结论进一步推广吗?类比实数乘法的运算,试探究向量数乘满足的运算律.
设计说明教师在追问中提出新问题,建构数学模型让学生独自去解决这一问题,可从向量的大小和方向分别去研究,也可以从图形去研究.
思考 依据实数的数乘运算律,向量数乘有哪些运算律呢?向量数乘与实数乘法有哪些相同点和不同点?
设计说明向量数乘建构过程表现为学生在教师的引导下,联想向量的加法、减法提出问题,解决问题,再提出问题,分析并解决问题,再发现问题,并解决问题等.让学生经历数学建构的实践活动过程,提升学生研究探索、语言表达的能力.
例2 已知向量a和向量b,求作向量-2.5a和向量2a-3b.
例3 计算:(1)3(a-b)-2(a+2b);
(2)2(2a+6b-3c)-3(-3a+4b-2c).
总结:向量的线性运算的结果是一个向量,其运算法则与多项式运算类似.
师:继续探究例1的前两个小题并思考——

设计说明建构数学概念的目的之一就是能够用建立的数学模型解决实际问题.通过例3之后的追问、反思,学生可以发现,向量的数乘可以解决两个向量的共线问题,表现在平面图形中,可以解决三点共线、两直线平行等问题.学生经历应用数学知识解决数学问题的过程,由此积累做数学、学数学、用数学的经验,增强数学的应用性意识.
数学概念的教学是使学生经历数学概念、结论产生的过程,体验数学在解决实际问题中的价值和作用.其一是对现实问题的数学抽象;二是用数学的三种语言(文字语言、符号语言、图形语言)表达问题;三是用数学方法构建模型解决问题.
3 落实“感觉、感知、感悟”教学法的思考
3.1 源于问题情境的初步感觉,提升阅读理解、信息整理素养
数学源于生产生活实际,数学知识的发生发展过程源于解决实际生活问题的过程.在课堂教学过程中,要创设合适的教学情境,启发学生思考.学生在与问题情境的有效互动中,通过对背景材料、实际问题的初步感觉,先初步了解实际背景是什么、其中蕴含了怎样的数学问题,学会将实际问题转化为数学问题.向量是既有大小又有方向的量,日常生活中的位移也是向量,所以“向量的数乘”这节课以物理量为背景抽象出向量数乘的概念,在教学中发展学生信息获取、知识整合的能力.
3.2 重在数学问题的体验感知,提升实践探索素养
“实践探索素养”是指学习者在面对生活实践或学习探索问题情境时,组织整合相应的知识与能力、运用不同的技术方法进行各种操作活动以解决问题的综合品质.课堂教学中,教师不是将“结论性知识和规律性方法”机械地交给学生,而要引导他们经历实际情境,通过提问、追问等方式,突出问题导向,通过问题驱动将学生的学习引向深入.学生通过自己的体验感知,解决问题,再提出新问题,分析问题,解决问题,建构数学模型.本课例类比向量的加法、减法的概念,引导学生运用文字语言、图形语言、符号语言表达向量数乘的定义.引导学生从已有的研究向量加法、减法的方法,类比熟悉的数的乘法运算律,建构向量的数乘运算律,学生通过思考发现问题,探究反思,解决问题,发展操作应用和数学表达的能力.
3.3 贵在对建构概念模型的反思感悟,探索思维方法素养
“思维方法素养”是指学习者在面对生活实践或学习探索问题情境时,进行独立思考和探索创新的内在认识品质.在课堂教学中,引领学生感悟知识产生的过程,在应用中积累数学思维和实践的经验.“向量的数乘”强调引导学生应用向量的数乘解决物理问题、几何问题.发现应用数乘的有关概念可以证明平面图形中的平行关系、研究平面图形中段落之间的关系等等.通过引导学生在多样化的数学活动中去思考、探索、发现结论,提升他们的数学建模与数学探究的能力.
在数学课堂上,应用“感觉、感知、感悟”教学法,从实际问题和背景中抽象出新的数学概念,建构新概念,建立新概念的运算,以及在数学问题、实际模型中应用新运算等.概念的教学过程可以描述为三个阶段:创设恰当的教学情境,提出合适的数学问题;启发学生思考,让学生理解数学概念的来龙去脉,建构数学概念,掌握基础知识,形成基本技能;感悟数学的思想,领悟知识本质,学以致用,在应用中积累数学思维和实践活动经验,形成和发展数学学科核心素养.通过初步感觉、体验感知、思考感悟,展现教学内容的过程性,实现活动的探索性,完成“四基”“四能”的教学,这是改变传统教学法[2],是有创新、融能力与素养的高品质数学教学,是落实学科素养的有效教学法.

