揭示数学本质 提升学生素养
——对“基本不等式的证明”教学的思考*
黄智华 (江苏省南京市秦淮区教师发展中心 210002)
1 基本情况
1.1 授课对象
学生来自四星级重点高中高一普通班,基础较好,有一定的自学能力、推理能力及运算能力,而且已经有了课前预习自学的习惯.
1.2 教材分析
所用教材为苏教版《普通高中课程标准实验教科书·数学(必修5)》.“基本不等式的证明”是第3章第4节的内容,这节内容由“基本不等式的证明”和“基本不等式的应用”两部分组成.基本不等式在后续的学习中是作为定理直接应用的,它在求函数最值、证明不等式方面有广泛的应用,课标要求熟练掌握、灵活运用,所以要让学生经历知识的发生、发展、应用、深化认识和理解的完整过程.基本不等式的证明及简单应用是本节课的重点.
教材给出了证明基本不等式的三种证法,分别是作差比较法、分析法和综合法,并在“思考”中给出了基本不等式的一种几何解释,可以认为是基本不等式的一种几何法证明.几何法证明是从图形的度量关系得到基本不等式,赋予基本不等式以几何直观,这种证明方法需要构造合适的图形,这也成为教学的难点,但它可以突出数形结合的数学思想,通过“数”与“形”两个方面加深学生对基本不等式的理解与掌握.
例1所承载的教学功能是基本不等式的简单应用,用它证明其他不等式,以此熟练掌握基本不等式.在实际教学中,学生延用比较法、分析法、综合法来证明,这符合学生认知规律;不同的证明方法可以活跃学生的思维,发展学生的思维能力.分析、比较各种证明方法,引导学生发现运用基本不等式来证明是最简洁的,它属于综合法证明不等式.必须追问:怎么会想到运用基本不等式来证明的?带领学生一起分析问题的结构特征:不等式左边是两个正数的和,右边是常数,可以看作是左边两个正数(互为倒数)的积,符合基本不等式的本质特征,所以可以直接运用基本不等式来证明.例1有两个小题,要揭示它们本质是一样的,都是求证“一个正数和它的倒数之和大于等于2”.
教学目标 (1)经历基本不等式的探究发现和逻辑论证的过程,体验、感受数学发现和创造的快乐,感知从特殊到一般、化抽象为具体的数学研究方法;
(2)会用作差比较法、分析法和综合法证明基本不等式,发展逻辑推理素养,理解几何法证明基本不等式,领悟数形结合思想,渗透数学文化,发展直观想象、数学建模素养;
(3)能用基本不等式证明其他相关的不等式,能够利用基本不等式求函数最值,突出体现整体换元法;
(4)能让学生从数学角度主动发现问题、提出问题和分析解决问题.
教学重点 基本不等式的证明及简单应用.
教学难点 基本不等式的几何法证明.
2 教学过程
2.1 基本不等式的探究及证明
问题1实数a,b的等差中项和等比中项分别是什么?


说明考虑到教材上的问题情境不太切合实际、学生解决起来有困难,所以教学就从数学内部提出问题引入课题,这更利于教学活动的有效开展,有利于突出教学内容的本质,有利于构建逻辑连贯、前后一致的教学进程,有利于发展学生的认知力.在学生思考问题1时,提出只有a,b同号才有等比中项,培养学生质疑和批判性思维.启发引导学生自己主动提出问题2,培养学生的问题意识.在猜想结论的时候,学生得出了错误的结论,教师便将错就错,让学生经历从错误走向正确的真学习过程,深化了学生对数学本质的认识.
问题3请同学们证明猜想出的结论.
方法1 作差比较法,具体证明过程略.
方法2 分析法,具体证明过程略.
方法3 综合法,具体证明过程略.
方法4 几何法,通过构造图形来证明.
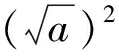
方法4应该是在学生课前预习自学的基础上给出的.追问学生是怎么想到的?这是本节课的难点.借此介绍“无字证明”,展示中国古代数学的成就,渗透数学史,提升数学文化素养.
2.2 基本不等式的内容及认识
·基本不等式
·两个数学概念

·深化对基本不等式的认识
通过设置以下四个问题深化对基本不等式的认识与理解:(1)基本不等式的文字语言表述是什么?(2)基本不等式成立的条件是什么?(3)基本不等式等号取得的条件是什么?(4)基本不等式所揭示的本质是什么?
一个数学对象通常可以用三种语言(文字语言、符号语言、图形语言)来描述,三种语言相互支撑、相得益彰,三种语言之间的相互转化可以加深学生对这一数学对象的认识.让学生经历“犯错—寻错—纠错”的探究过程,深化学生对基本不等式成立条件的认识.等号取得的条件是在学生证明过程中加以强化的.基于现在的学生学习了很多数学知识不知道怎么用,什么时候该用、什么情况下能用,提出问题(4).通过学生独立思考、相互交流讨论,得出结论:给出了两个正数的和与积之间的不等关系,这其实也是基本不等式的结构特征.这些认识为学生正确运用基本不等式解决问题奠定了扎实的基础.
2.3 基本不等式的应用及深化
例1设a,b为正数,证明下列不等式成立:
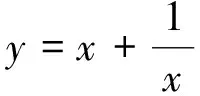
适度拓展的目的是引起学生对基本不等式成立条件的重视,这是学生今后运用时的易错点.通过拓展训练给学生思考、辨析机会,可以深化学生对所学新知的认识,同时渗透分类讨论、化归转化等数学思想,培养学生思维的严谨性,优化学生的思维品质,发展学生的数学能力,提升学生的数学素养.
2.4 课堂小结
数学知识角度:基本不等式的内容、结构特征、证明方法以及简单应用.
思想方法角度:从特殊到一般进行猜想,然后论证猜想结论,突出数学研究方法;体现化归转化、数形结合、分类讨论等数学思想.
核心素养角度:直观想象、逻辑推理、数学运算、数学建模等.
2.5 课后探究及课后作业
课后探究:现有一台天平,两臂长不相等,其余均精确,有人说要用它称物体的重量,只需将物体放在左右托盘各称一次,则两次所称重量的和的一半就是物体的真实重量.这种说法对吗?说明你的结论.
课后作业:教材第98页练习1~2,第101页习题1~2.
3 教学反思
3.1 学生的自学要学到真知识,课堂教学要让学生经历真学习
现在很多的课改提倡“先学后教”“少教多学”,旨在突出学生学习的主体地位.学生的自学是不是真正能学懂,是不是能抓住数学的本质,是否提出有价值的问题,是否能学到数学研究方法、领悟蕴含其中的数学思想,这些都值得关注和研究,课堂教学要让学生经历真学习.
3.2 创设问题情境让学生多角度、多层次认识和巩固新知
其次是让学生自主证明猜想得到的结论,出现了不同的证明方法,特别是几何证明方法的出现,让学生从“数”与“形”两个方面来认识、掌握基本不等式.通过证明,让学生既确信基本不等式是正确的,又学到了数学研究的方法.
再次是设计了四个小问题帮助学生深化对基本不等式的认识,目的是让学生能正确使用基本不等式、弄清楚基本不等式的本质以及能解决什么问题.
最后是讲解例1和变式拓展,加深学生对基本不等式成立条件和本质的认识.
3.3 关注数学思想方法的教学,使教学更富有思想性
本节课的教学有意识地渗透了“化归转化”“分类讨论”“数形结合”“化抽象为具体、从特殊到一般”等数学思想方法,重点突出了“数形结合”的数学思想.

图1 图2 图3
其次,借助学生熟悉的初中知识介绍“无字证明”——通过构造图形来证明数学命题,给出了学生熟悉的公式(a+b)2=a2+2ab+b2的无字证明(图2).
最后让学生从我国古代数学家赵爽给出的“勾股定理”的无字证明(图3)中找出“基本不等式”(这是人教版教材的引入设计),既培养学生识图能力、整体代换能力,突出基本不等式的几何背景,更提升学生的数学文化素养.
渗透数学思想方法的教学增加了课的内涵,丰富了数学教学的思想性,从而促进了学生思维的深入,其学习就有了深度.数学思想是数学的灵魂,与数学基本方法一起常常在学习掌握数学知识的同时获得,提高数学素养的核心就是提高学生对数学思想方法的认识和运用.

