动态光散射中非负最小二乘反演算法的研究*

李开玮 ， 张智明 ，李振华

（1.广东理工学院智能制造学院，广东 肇庆 526100；2.广东理工学院大学物理实验中心，广东 肇庆 526100）

0 引言

纳米颗粒具有表面效应和小尺寸效应，在环保、生物等技术上被广泛应用，纳米颗粒的尺寸分布对于它的应用来说是一个重要的参数[1-3]。在测量粒径尺寸的方法中，动态光散射具有实时、快速、无损的优势，因而得到了广泛的应用[4-5]。动态光散射是基于液体中悬浮粒子的布朗运动，布朗运动将导致散射光强随时间涨落，通过散射光的相关分析得到散射光的光强自相关函数，该函数包含了粒子的尺寸信息，通过反演算法可以获得粒径尺寸分布。该反演算法的主要功能是求解一类Fredholm积分方程，该方程是一个病态问题，为了提高反演结果的精确性，基于不同的理论，许多优化算法被提了出来。主要的优化算法有累积量法[6-7]、非负最小二乘法[8-9]、约束正则化算法[10]等，每种算法都有自己的优势和缺点，其中非负最小二乘法因原理简单、结果精确且能给出尺寸分布函数而得到广泛应用。

本文接下来将以第一部分介绍非负最小二乘反演算法原理，第二部分介绍程序算法及模拟内容，最后总结非负最小二乘法在动态光散射中的应用方法。

1 动态光散射中非负最小二乘反演算法原理

在动态光散射实验中，入射光以一角度照射在样品上，由于颗粒的布朗运动，散射光强将产生涨落现象，对散射光信号进行相关分析可得到光强自相关函数g(2)(τ)，它与光场自相关函数g(1)(τ)具有Siegert关系，如式（1）所示[11]。

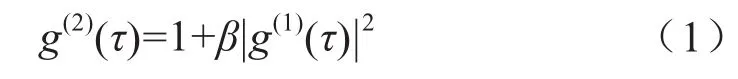
其中，β是光学相干因子，τ是延迟时间。而粒子尺寸分布PSD与g(1)(τ)的关系如式（2）所示[12]。

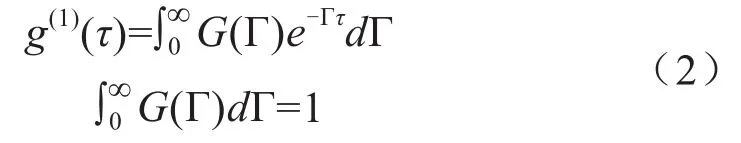
其中，Γ是衰减线宽，G(Γ)是归一化衰减线宽分布函数，Γ与粒子尺寸关系如式（3）所示。

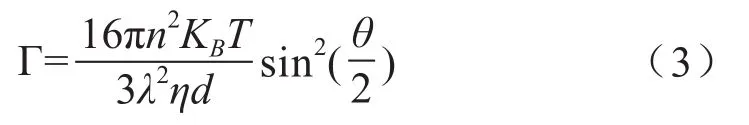
其中，d是粒子直径，n是液体折射率，KB是玻尔兹曼常数，T是液体绝对温度，λ是入射光的波长，η是液体的粘滞系数，θ是散射角。当求解积分方程式（2）得到G(Γ)后，可根据式（3）得到粒径尺寸分布PSD。

为了计算G(Γ)，将式（2）离散化得到式（4）：

其中，N是粒子尺寸分布的离散点个数，M是相关器的通道个数。式（4）可以被表示成非负最小二乘问题。

其中Aij=exp(-Γiτj)是一个M×N核矩阵，bj=g(1)(τj)是实验中相关器通道获得的数据，xi=G(Γi)是所要求的解。由于M≠N且b中含有噪声误差，因此式（5）无法求得精确，只能得到最优解，通过使||Ax-b||2最小，如式（6）所示，即可得到最优解。

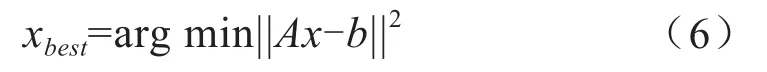
2 模拟研究

为了得到粒子尺寸分布PSD，求解式（5）即反演算法显得至关重要，本文以最小二乘法原理为基础[13]，加上非负约束，编写了反演算法程序，用来求解式（6）。反演过程如下：首先设定粒子尺寸分布数组｛d1,d2,...dN｝，相邻两个尺寸间隔Δd=dk+1-dk设置为相等，然后由式（3）求得衰减线宽数组｛Γ1,Γ2,...ΓN｝，再设定延迟时间数组｛τ1,τ2,...τM｝，创建核矩阵A，然后利用A及实验数据b，通过非负最小二乘法求解粒子尺寸分布的最优解xbest。

反演算法中，需要对粒子尺寸作离散化处理，是否选择了合适的粒子尺寸范围和粒子尺寸间隔Δd创建核矩阵，对反演结果精确性有着很大的影响[12-14]。另外在实验中b中含有的噪声信号也会影响反演结果的可靠性[15]。因此在做实验前有必要研究反演结果与以上各因素之间的关系。

假设粒子尺寸分布理论值为单峰高斯分布。

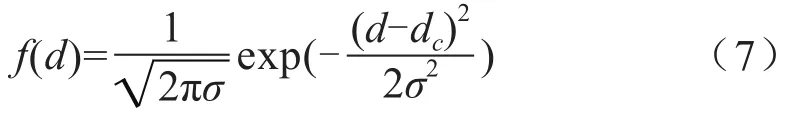
其中，dc为粒子中心尺寸，σ为峰宽，在模拟中选取实验参数为KB=1.38× 10-23J/B，T=298.15 K，η=0.89 Pa·s，n=1.331 6，λ=632.8 nm。

首先利用程序反演窄带高斯分布，设dc=200 nm，σ=10 nm，通过程序反演了不同步长Δd下的粒子尺寸分布PSD，图1为Δd从5 nm到15 nm变化时的反演粒径尺寸分布，当步长小于σ时，如图1（a）所示，粒径尺寸分布出现许多错峰；而当步长大于σ时，如图1（b）所示，粒径尺寸分布接近真实值，峰值尺寸也十分接近真实值，很好地反映出了粒子尺寸分布PSD。

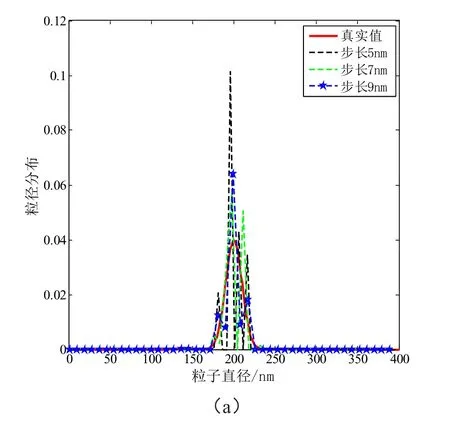
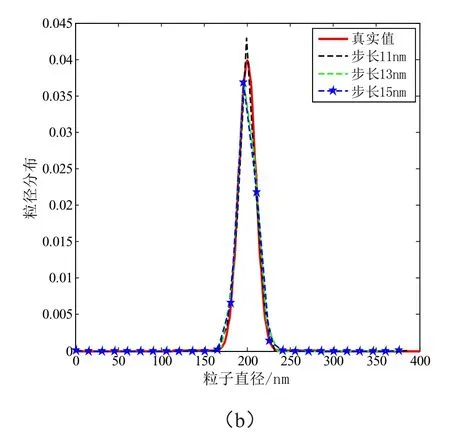
图1 不同步长下窄带高斯分布反演粒径分布

接下来利用程序反演宽带高斯分布，设dc=200 nm，σ=30 nm，图2为Δd从5 nm到40 nm变化时反演的粒径尺寸分布，如图2（a）可以看到当步长小于σ时，粒径尺寸分布出现多峰，与真实分布有较大差距；再看图2（b），当步长大于σ时，粒径分布变为单峰，与真实分布几乎一致，精确性提高了许多。

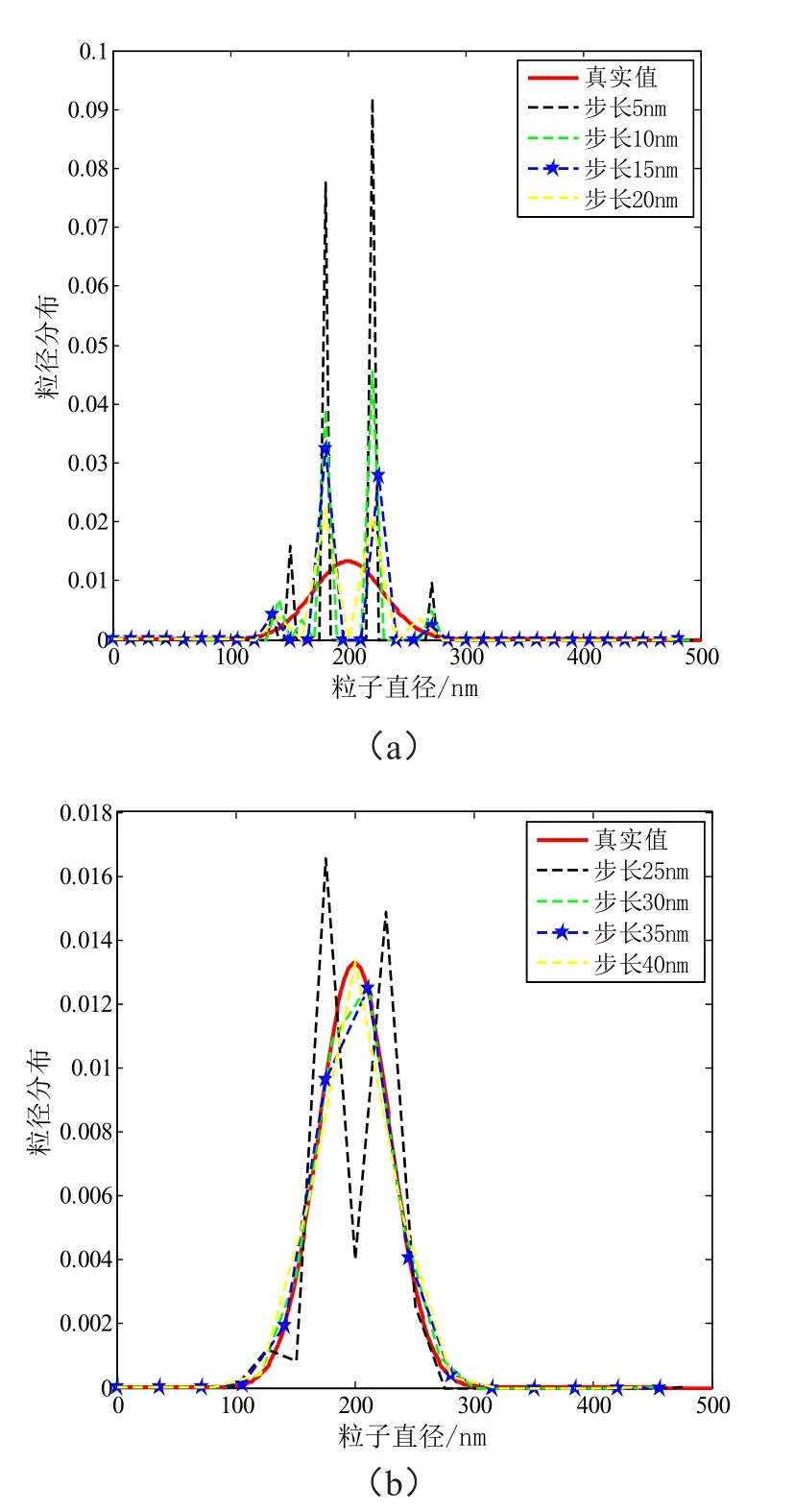
图2 不同步长下宽带高斯分布反演粒径分布

紧接着，模拟实验情况，给b加上噪声信号，探讨程序反演算法的抗噪声性能，设dc=200 nm，σ=10 nm，Δd=10 nm，图3为噪声从0.001到0.011时的反演粒径尺寸分布图，由图3可知，在存在噪声的情况下，峰值都会增高，粒径尺寸分布仍为单峰分布；当噪声小于0.005时峰值处粒径与真实值接近，但峰宽σ收窄；当噪声大于0.005后，峰值处粒径与真实值有一定的偏离，总体来说，反演程序具有较好的抗噪声特性。

图3 不同噪声水平下反演粒径分布

3 结论

通过以上的模拟可以发现，反演结果与粒径的步长密切相关，当步长小于σ时，反演结果具有多个峰，而且非常尖锐，与真实值差别大；当步长大于σ，或在σ附近时，反演结果具有较高的精确性。在抗噪声方面，当噪声比较小时，反演结果能够保持精确性，但反演的峰宽σ变小；当噪声偏大时，反演结果有较大偏离。总体而言，该程序具有较好的抗噪声性能。

在实际的实验当中，粒径分布是未知的，b由实验给出，可以通过改变步长的方法，利用非负最小二乘法程序反演出粒径分布，然后比较不同步长下的反演结果，选出最优步长，再利用最优步长进行反演计算，最终得到非常精确的粒径分布。