图们江流域洪水灾害危险性评价实验设计研究

夏晓琢，邹嘉琪，金光日，权赫春*，林哲浩

(1.延边大学 地理与海洋科学学院，；2.延边大学 工学院：吉林 延吉 133002 )

洪水灾害主要是指由于大气降水的不规则运动所引起的洪水给人类正常生活、生产活动带来的损失与祸患，具有复杂性、不确定性、高维性、动态性、开放性和非线性等特点[1-2]。近年来，GIS(Geographical Information System)技术的发展为洪水灾害提供了数据管理工具、空间分析功能以及直观的表现手段，使得洪水灾害研究有了新的突破[3]，对于洪水灾害预测的方法也逐渐增多。

尽管我国洪水灾害研究相较于国外要晚些，但近年来国内也涌现了诸多学者采用多种不同方法对洪水灾害的危险性进行评价。如2000年周成虎等[4]在层次分析法计算下以降雨、地形和社会经济易损性为主要指标，划分辽河流域为洪水灾害危险区；2013年殷洁等[5]基于灾害系统学，运用层次分析法(Analytic Hierarchy Process，AHP)，构建了武陵山区风险评估指标体系；2017年刘鑫等[6]以伊犁河流域为研究对象，运用信息量法和GIS空间分析对该区春季融雪型洪水危险性进行评价等。2021年，Li 等[7]考虑坐标、高程、坡度、不透水性、土地利用、土地覆盖、土壤类型等因素，利用朴素贝叶斯、感知器、人工神经网络和卷积神经网络等机器学习算法，生成洪水危险性图。2021年Islama等[8]运用人工神经网络(Artificial Neural Network,ANN)、支持向量机、随机森林、随机子空间(Random subspace method，RSM)模型等进行组合，分别预测孟加拉国北部提斯塔河流域的洪水危险性，并通过实测数据验证比较每种模型的精度。

综上所述，对于不同的评价方法和不同的灾害影响因子的选择会导致危险性评价精度的不同。为有效提高图们江流域洪水灾害的危险性评价精度，该研究基于3种不同方法和灾害影响因子设计了基于GIS的洪水灾害危险性判别试验。具体包括洪水灾害因子的选取、模型的构建及危险性评价、模型精度验证及对比分析和洪水灾害危险性区划制图等。

1 试验目的

图们江流域位于中、朝、俄3国边境交界处。南边以图们江为界，与朝鲜隔江相望，东部与俄罗斯接壤，地理坐标为41°59′N～44°30′N、127°27′E～131°18′E(图1)。总流域面积33 168 km2，河道总落差1 297 m，平均坡降1.2‰。根据2015年年平均气温和降雨量数据显示，图们江流域内年平均气温为摄氏2°～6°，年平均降雨量为551～700 mm。图们江流域内河网水系的分布十分密集，地形起伏大，因此，一旦受强降雨就会发生严重的洪水灾害。为有效评价图们江流域洪水灾害危险性，该研究设计了图们江流域洪水灾害危险性进行评价的试验研究，并根据评价结果，为当地防灾减灾提供一定的依据和参考。

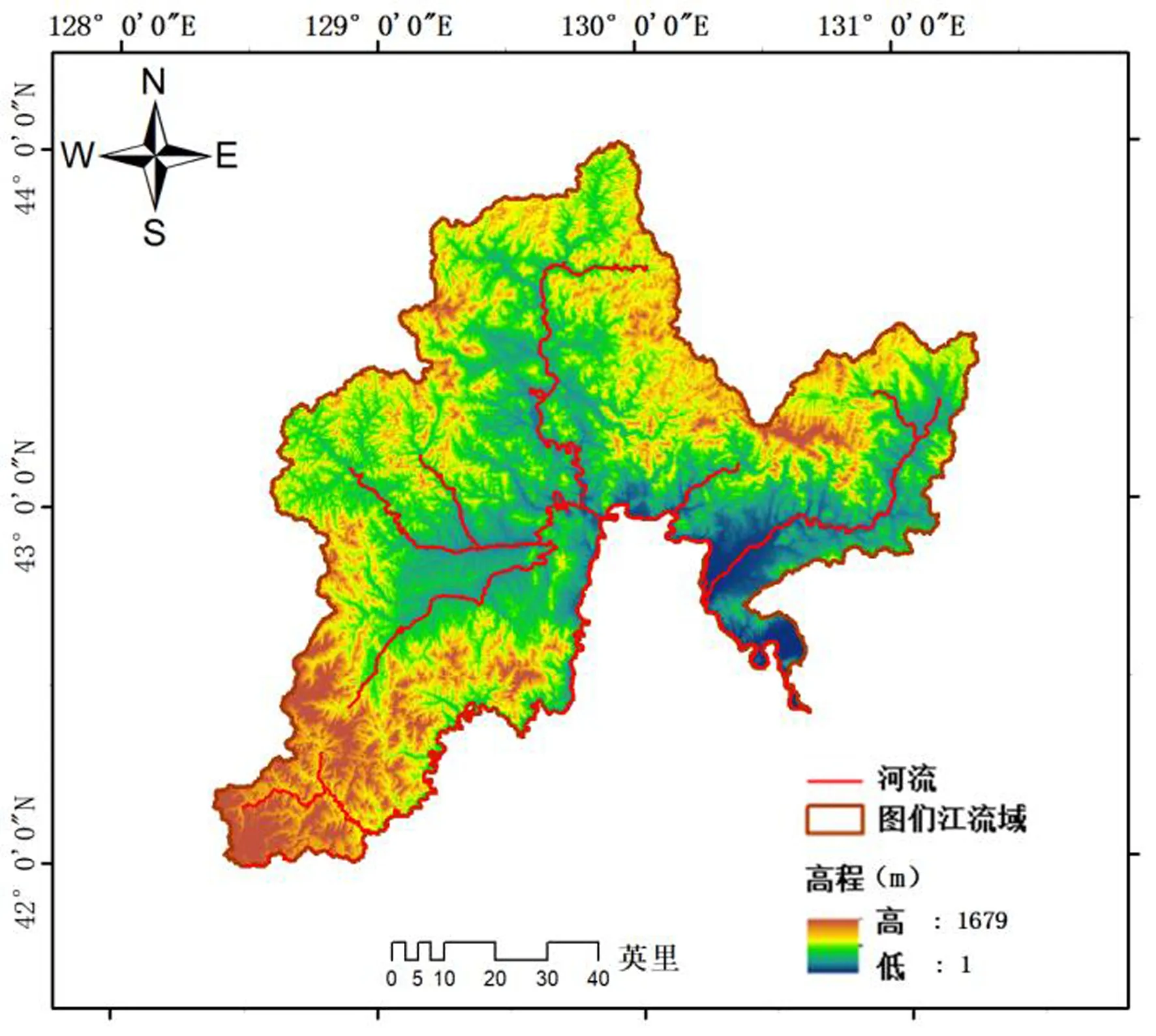
图1 研究区域

2 试验方案

图们江流域为研究区域(图1)，基于GIS技术，利用层次分析法、信息量法和随机森林机器算法3种模型对研究区内洪水灾害危险性进行评价。试验主要包括以下几个方面：1) 选取洪水灾害危险性评价因子并进行量化和归一化处理；2) 构建基于层次分析法、信息量法和随机森林算法下图们江流域洪水灾害危险性评价模型；3) 分别对各模型计算下的危险性进行评价；4) 根据灾害点分布情况对3种模型危险性预测结果进行精度对比分析和评价，并绘制研究区内洪水灾害危险性区划图(图2)。

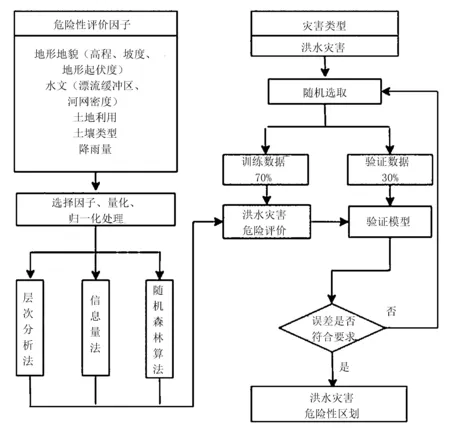
图2 试验流程图Fig.2 Experimental flow chart

3 试验过程

3.1 洪水灾害危险性评价因子选择与处理

通过参考以往学者对图们江流域洪水灾害方面的研究和近年来实际受灾情况分析，该研究从多个方面分别选择了8个因子进行研究，包括地形地貌因子(高程、坡度、地形起伏度)、水文因子(河流缓冲区、河网密度)、土地利用、土壤类型和降雨量。其中，高程和坡度图是通过Arcmap10.2软件和DEM数据生成，其中高程通过自然断点法划分为15～321、321～531、531～729、729～971和971～1 640 m 5个等级(图3)。坡度同样划分为0°～5°、5°～12°、12°～19°、19°～28°和28°～86°等5个等级(图4)。地形起伏度图层由Arcmap10.2中块统计功能分别计算最后再进行差值计算生成，由计算结果可知图们江流域内地形起伏度范围为0～196 m，对其进行分级处理，划分为0～17、17～32、32～47、47～66和66～196 m等5个等级(图5)。由于图们江流域内水系众多，因此在河流缓冲区因子评价中使用筛选功能，将次级流域以下的分支水系进行筛选，留下主要河流干道根据不同高程建立多环缓冲区进行评价(表1)，并作图(图6)。将图们江流域所有水系分布进行密度分析可得图们江流域内河网密度值为0～1.89 km/km2，将其划分为0～0.39、0.39～0.61、0.61～0.83 、0.83～1.1和1.1～1.89 km/km2等5种不同等级，分别为Ⅰ、Ⅱ、Ⅲ、Ⅳ、Ⅴ(图7)。根据图们江流域的土地利用情况图层，可以将其分为耕地、林地、草地、湿地、水体、人造地表和裸地7种不同类型[9-10](图8)。考虑不同土壤的性质和发育情况，对图们江流域内土壤进行划分，分为Ⅰ(平积土、新积土)、Ⅱ(灰化土、灰粽壤、暗棕壤)、Ⅲ(沼泽土、草甸土、灰炭土)、Ⅳ(白浆土、水稻土)和Ⅴ(石灰岩土、石质土、风化土)5类(图9)。根据中科院发布的2011—2015年全国平均降雨量数据，提取图们江流域内年平均降雨量，并划分为525～557、557～579、579～599、599～619和619～653 mm等5个等级(图10)。

表1 缓冲区各等级信息Table 1 Information of the buffer levels

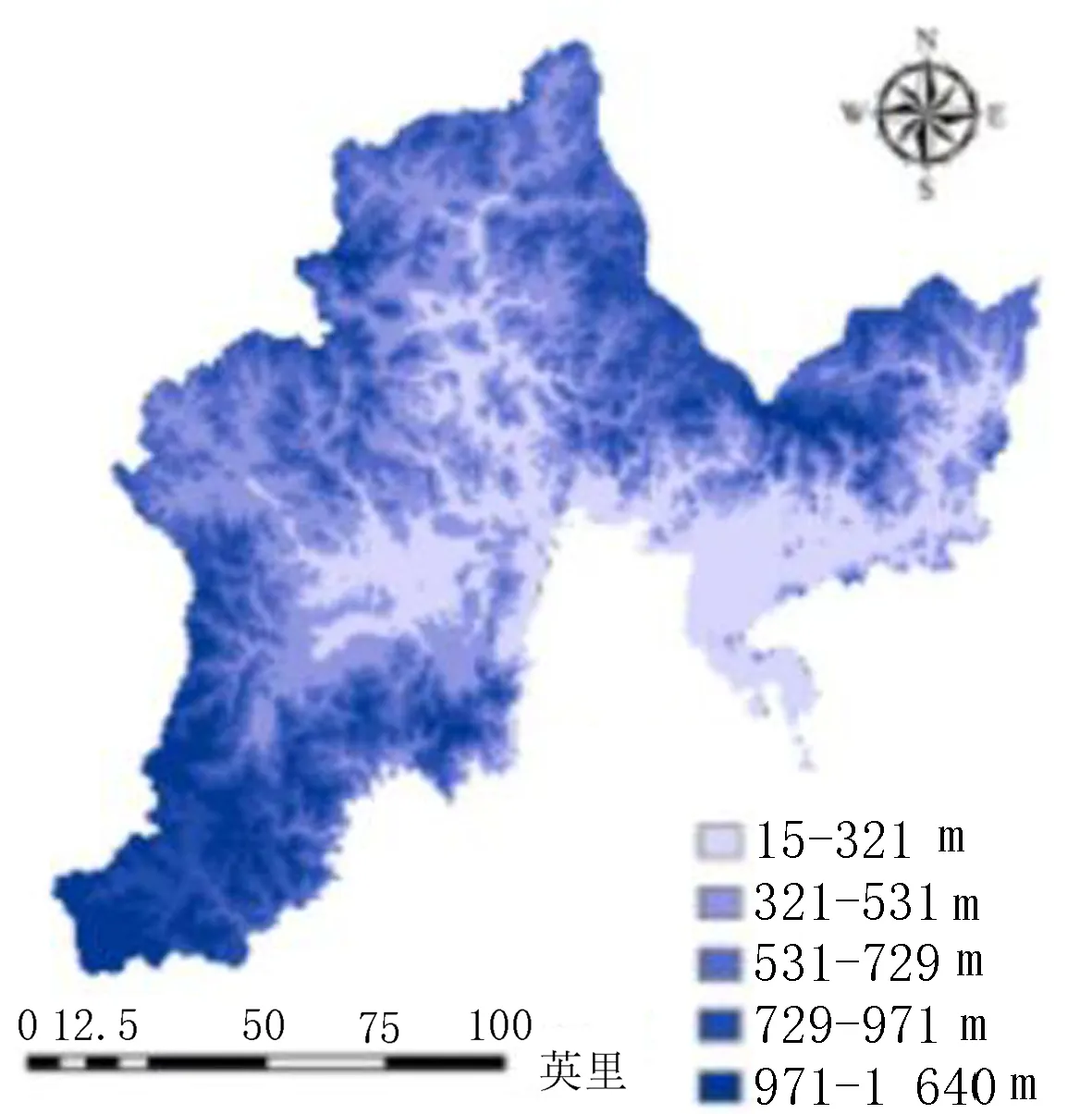
图3 高程分级图Fig.3 Elevation Classification diagram

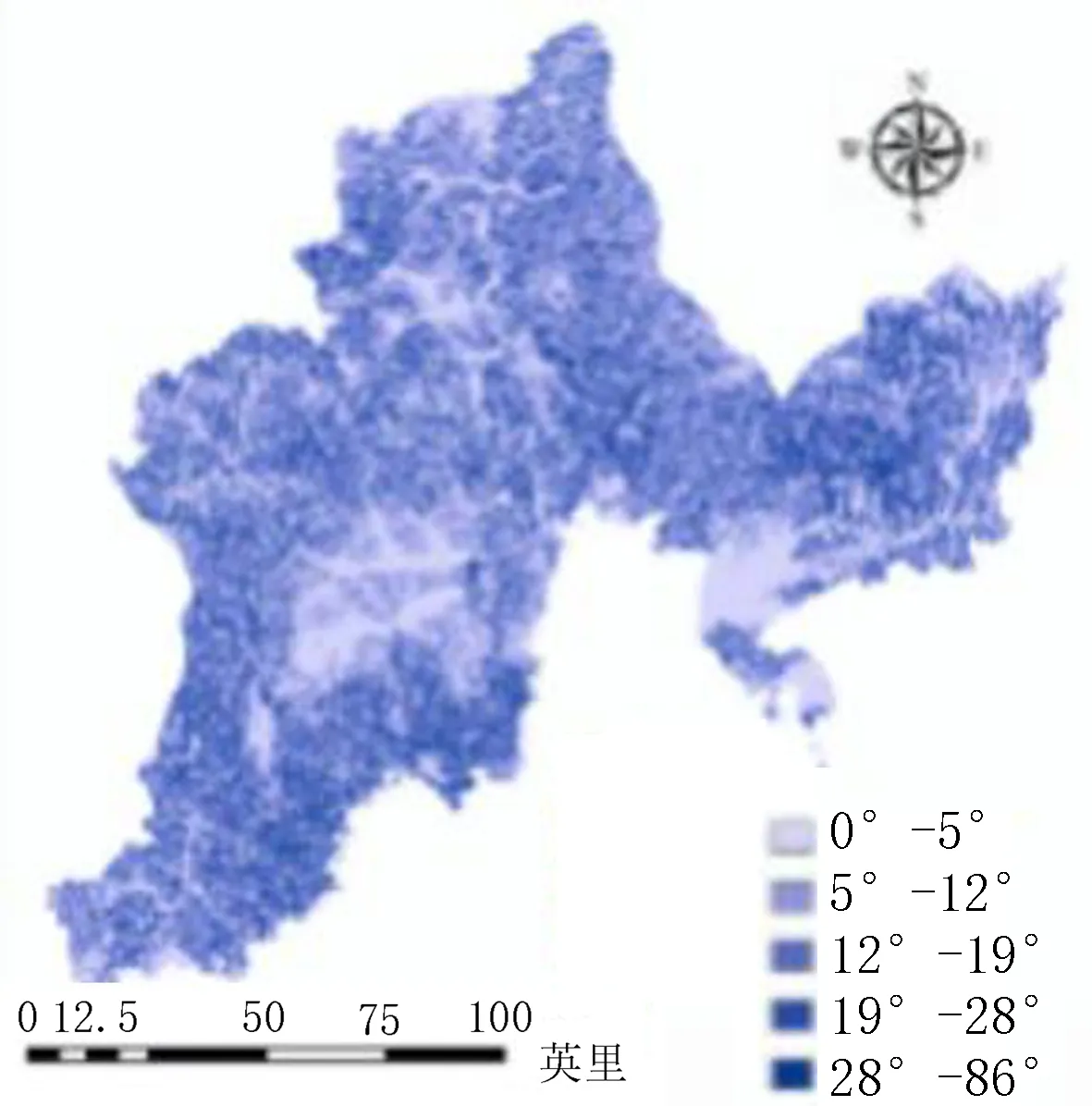
图4 坡度分级图

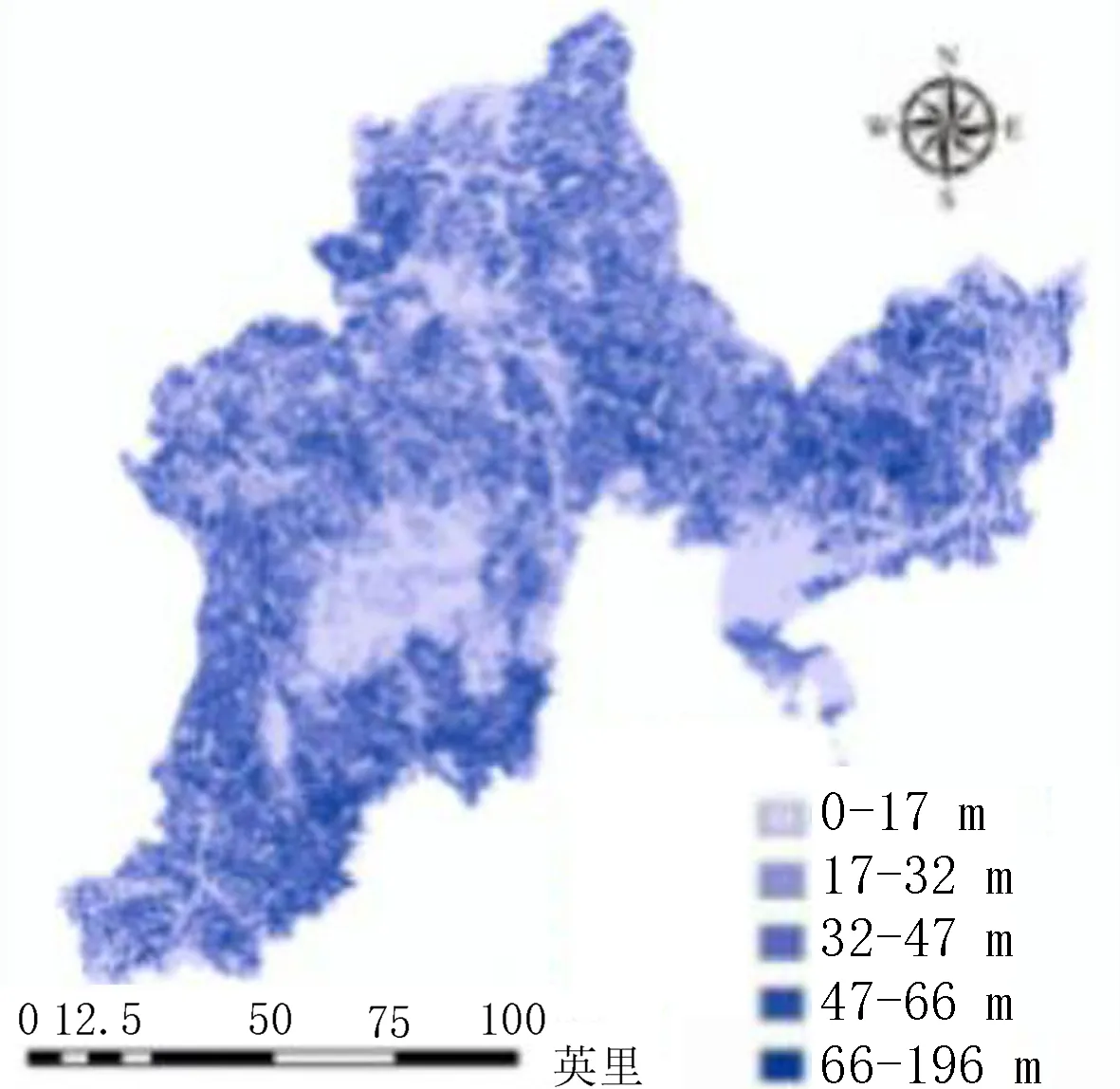
图5 地形起伏度分级图Fig.5 topographic grading map

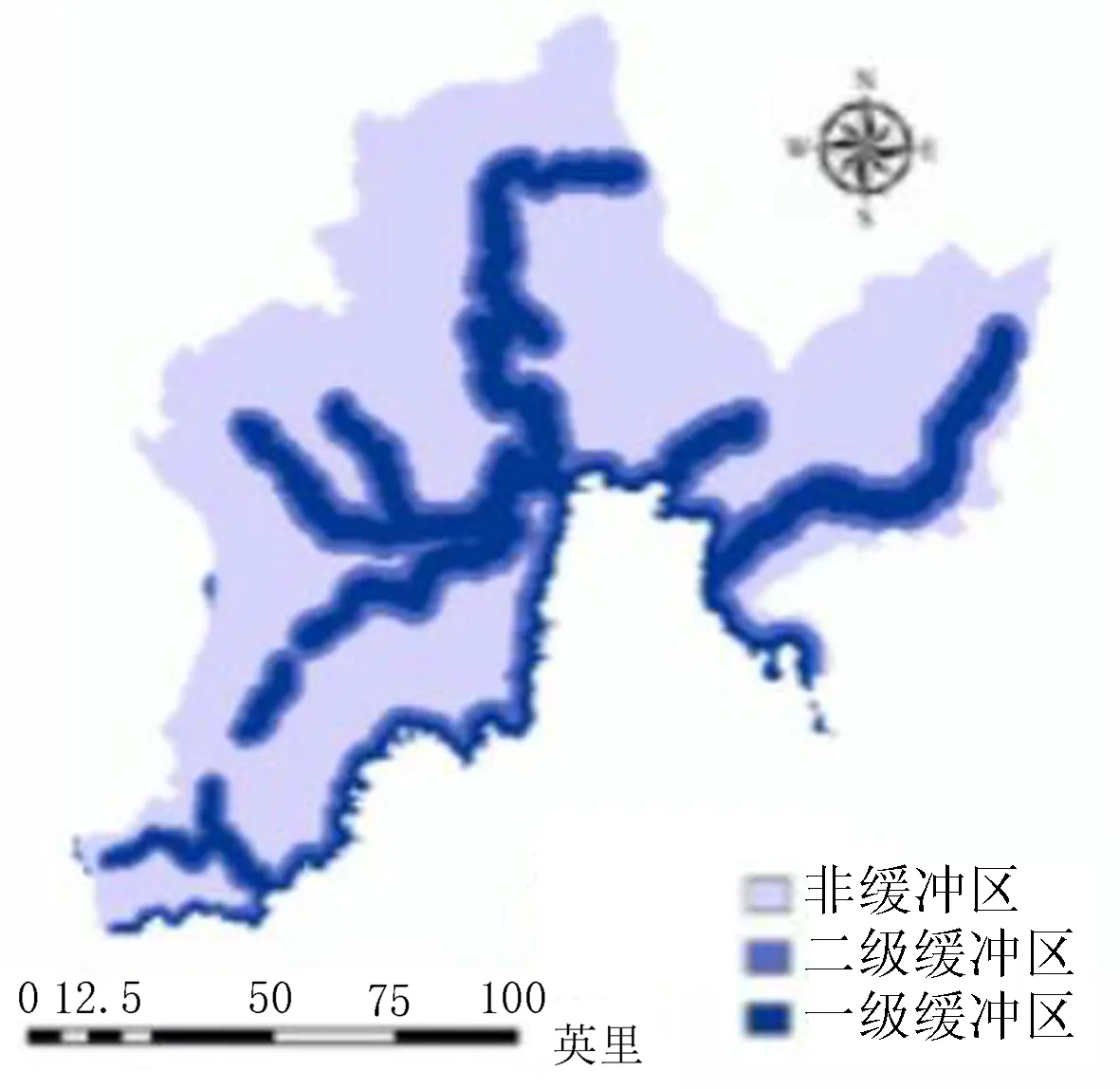
图6 河流缓冲区分级图

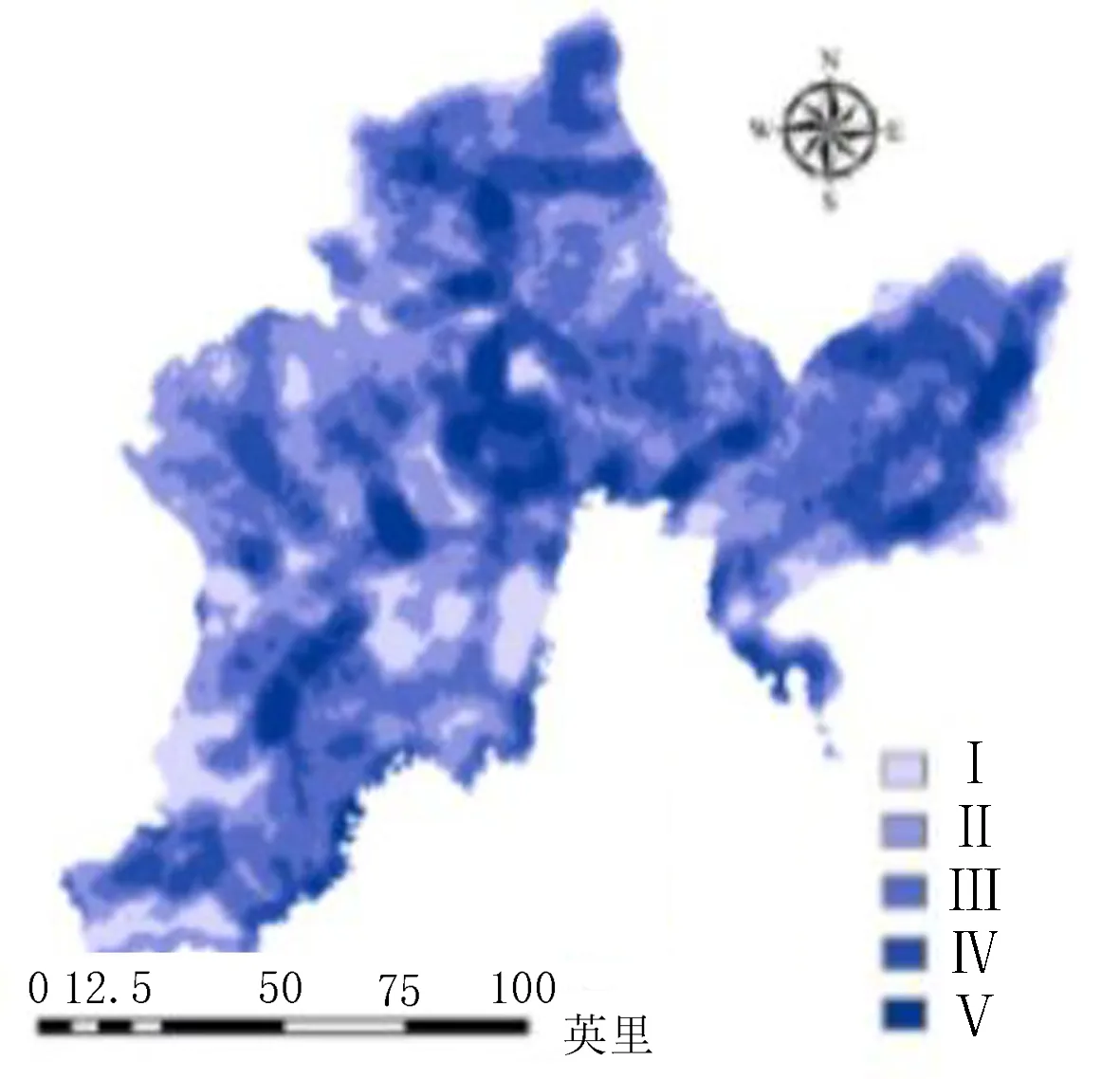
图7 河网密度分级图Fig.7 The density classification diagram of the river network

图8 土地利用分级图

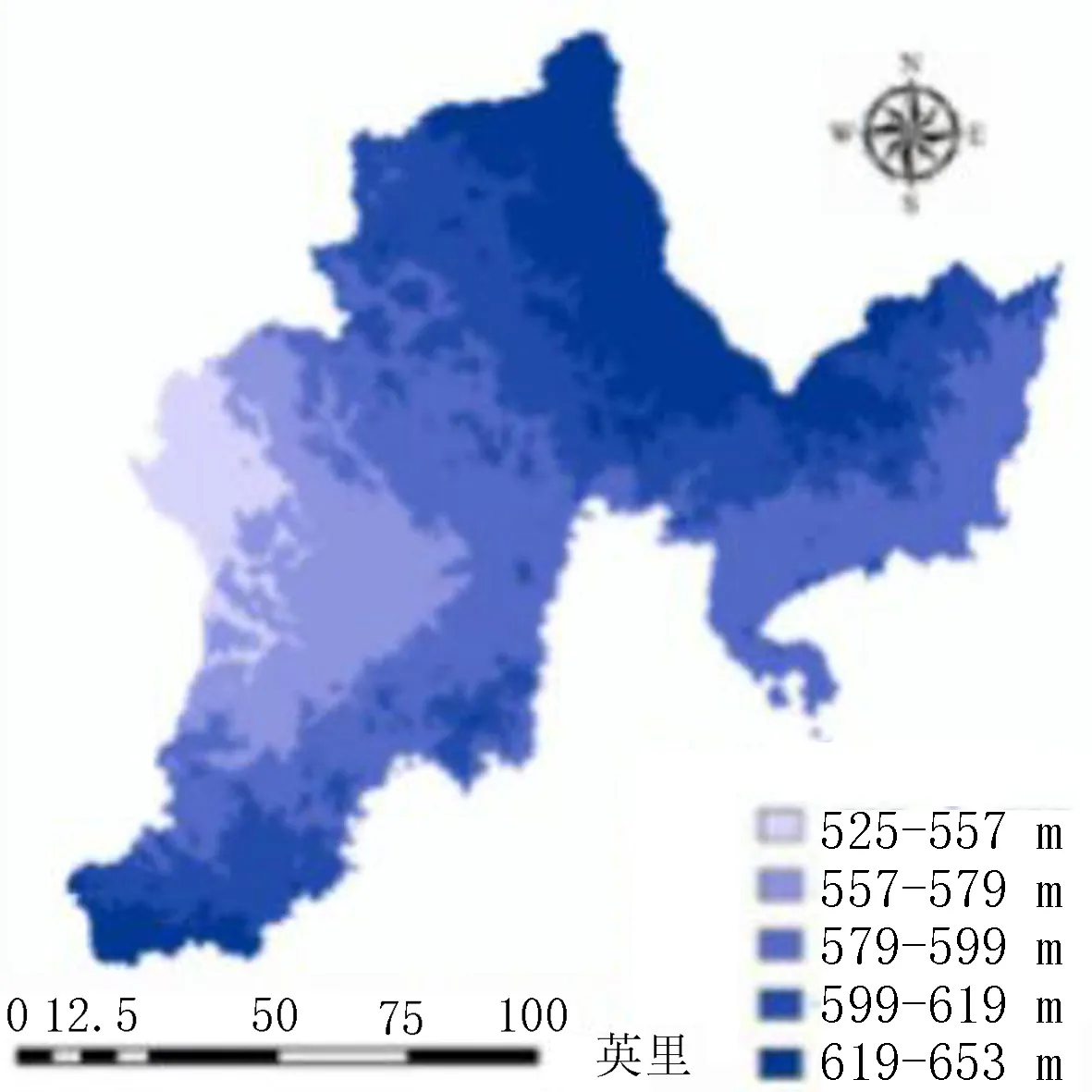
图10 降雨量分级图

3.2 构建图们江流域洪水灾害危险性评价模型

3.2.1 层次分析法

层次分析法是由美国学者Saaty T L于20世纪70年代在运筹学中提出的一种将决策有关的元素分解成目标、准则、方案等层次[11]，在此基础上进行定性与定量相结合分析的决策方法。它是一种灵活而又实用的多准则决策方法[12]。由于危险性研究中因子数量较多(8个因子)，构造的判断矩阵阶数较高，计算权重和一致性检验算数过程复杂，因此借助Matlab 2019软件进行计算分析。

根据对其它文献[13-16]的学习和专家意见，以及洪水灾害中各因子的影响程度大小，结合图们江流域实际洪水受灾情况构造判断矩阵，由计算结果可得地形起伏度相对权重值为0.302 7,河流缓冲区为0.219 8,河网密度为0.154 5,高程为0.080 3,降雨量为0.112 0,坡度为0.057 8,土地利用类型为0.039 8、土壤类型为0.028 4，并通过一致性检验。根据相对权重值，构建基于AHP的图们江流域洪水灾害危险性计算模型，即:

H=0.302 7×地形起伏度+0.219 8×河流缓冲区+0.154 5×河网密度+0.112 0×降雨量+0.080 03×高程+0.057 8×坡度+0.039 8×土地利用类型+0.028 4×土壤类型。

(1)

参考以往学者的经验和图们江流域实际洪水灾害发生情况和表2的参考值[17-18]，对地形起伏度、高程、坡度由低到高5个等级分别赋9、8、7、6、5。对降雨量和河网密度由低到高5个等级分别赋5、6、7、8、9。考虑不同土壤类型对洪水灾害发育影响具有一定差异，对Ⅰ、Ⅱ、Ⅲ、Ⅳ、Ⅴ类分别赋9、5、8、7、6。对河流缓冲区一级缓冲区赋9、二级缓冲区赋8、非缓冲区赋5。土地利用类型中对林地、湿地、草地、耕地和水体、人造地表、裸地分别赋5、6、7、8、9。

表2 因子权重参考值Table 2 Factor weight reference values

3.2.2 信息量法

信息量法起源于矿产预测技术，随着计算机技术的日益成熟和GIS技术的稳步发展，慢慢被应用到地质灾害预测中[19]。在洪水灾害预测中，信息量法可以通过对已有的灾害发生点的各种信息总结出易发生灾害的规律，即各类因子对洪水灾害发生所作出的贡献值，转化为信息量值，以此来作为各类因子重要性判别的标准。在该文运算中使用公式(2)来对各因素对洪水灾害所贡献的信息量值进行计算：

(2)

式中，Ni表示影响因素xi作用范围内洪水灾害单元的面积，N表示研究区内全部洪水灾害分布单元的面积，Si表示图们江流域内含影响因素xi的单元面积，S表示整个图们江流域的面积。

(3)

式中，I表示各栅格单元在多影响因素贡献的信息量值进行求和后的总信息量值，n表示印象因素的数量。最终计算得出的某评价单元内若I>0，则代表该单元有利于洪水灾害发生，且虽其值增大，该单元遭受洪水灾害的可能性越大，风险程度越高。I<0则相反。

该研究共选取了156个已发生洪水事件和102个未发生洪水事件的数据。这些数据是通过现场调查、网络报道、历史灾害调查资料等收集获取的。在此部分信息量值计算中选取70%(181个)的灾害点进行计算，剩余30%(77个)部分用作检验。前文中已经将各影响因子进行了分级和面积统计，可以根据式(2)对各影响因子不同分级状态的信息量值进行计算。在Arcmap10.2中分别叠加图们江流域内洪灾害分布点与8个因子的分级图层，使用Spatial Analyst工具中提取分析的值提取至点功能，即可将灾害点在某影响因素下的不同属性提取出来，在此基础上进行统计分析和计算，可以得到不同影响因子的各状态等级下的信息量值。

3.2.3 随机森林算法

随机森林(Random forest)是一种机器学习算法[20]。随机森林模型的工作原理是对随机抽样产生的多个决策树的结果进行分类处理，选择最优分类作为最终结果[21]。对比于目前已有的多种机器算法，随机森林具有其自身比较突出的优点，它的处理过程高效快捷，能对大量的输入变量进行高效处理，而且它可以对输入变量的重要性进行评判[22]。在该文中，使用随机森林算法输出的不同指标的重要性，将作为权重计算指标对洪水灾害危险性进行预测。

该研究随机森林算法中输入的样本数据包括2大类：1) 已发生洪水灾害的数据点的各类属性特征；2) 未发生洪水灾害的数据点的各类属性特征。样本数据主要包括8个因素(降雨量、高程、坡度、地形起伏度、土地利用类型、河网密度、河流缓冲区、土壤类型)的不同特征值，其中，灾害点样本数据来自随机选取70%的灾害点，剩余30%灾害点用作评价随机森林算法下不同重要性指标与相对应因子进行结合后的洪水灾害危险性预测图的精度，非灾害点则输入全部。

随机森林算法可以通过多种方式实现，比如使用Matlab建模，python软件或者利用R语言编写程序进行计算。该研究采用R语言，在RStudio软件中导入样本数据的各类属性特征值表编写程序进行不同指标的重要性运算，可得如图11所示变量重要性的折线图。

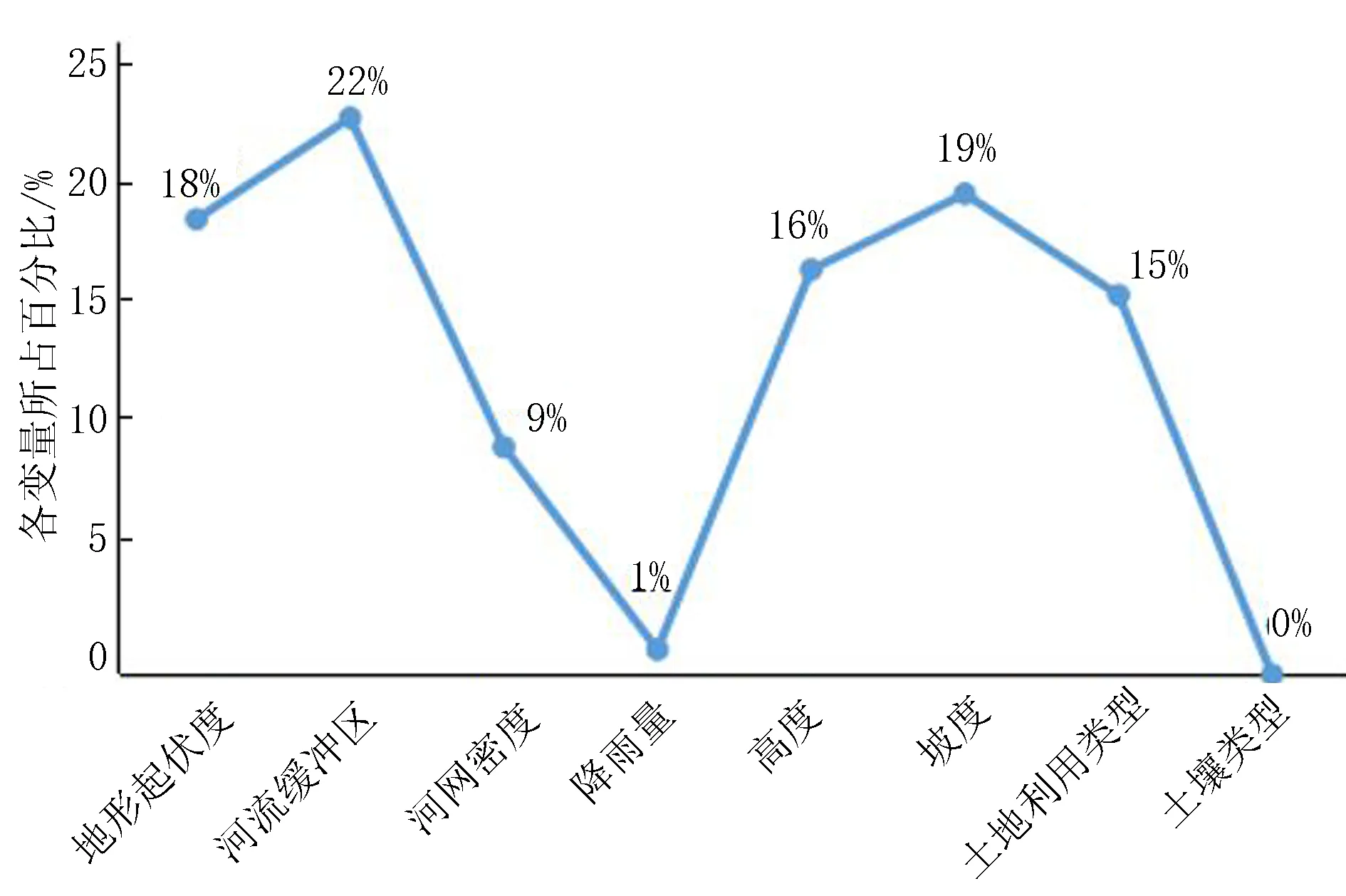
图11 变量重要性折线图

由图11可构建基于随机数森林重要性评价的图们江流域洪水灾害危险性评价模型，即

H=0.18×地形起伏度+0.22×河流缓冲区+0.09×河网密度+0.01×降雨量+0.16×高程+0.19×坡度+0.15×土地利用类型。

(4)

4 试验结果及对比分析

4.1 基于层次分析法模型的洪水灾害危险性评价

根据层次分析法计算得出权重构建的图们江流域洪水灾害评价模型(式1)并进行风险等级划分，可得层次分析法计算下图们江流域洪水灾害风险等级区划图(图12)，危险性等级由低到高分别划分为Ⅰ、Ⅱ、Ⅲ、Ⅳ、Ⅴ级。

图12 基于层次分析法的洪水灾害危险性区划图

各风险区面积从低风险到高风险分别为4 975.2、8 955.36、8 623.68、6 301.92和4 311.84 km2，占比分别为15%、27%、26%、19%和13%，在各级风险区中洪水灾害点的占比分别为0、3%、9%、27%和61%(图13)。FR(Frequencyratio)值是滑坡灾害点百分比除以滑坡危险性各等级面积百分比得出的值，可以对比分析不同模型形成的危险性评价精度。该方法得出的最危险区域(V级)FR值为4.69。

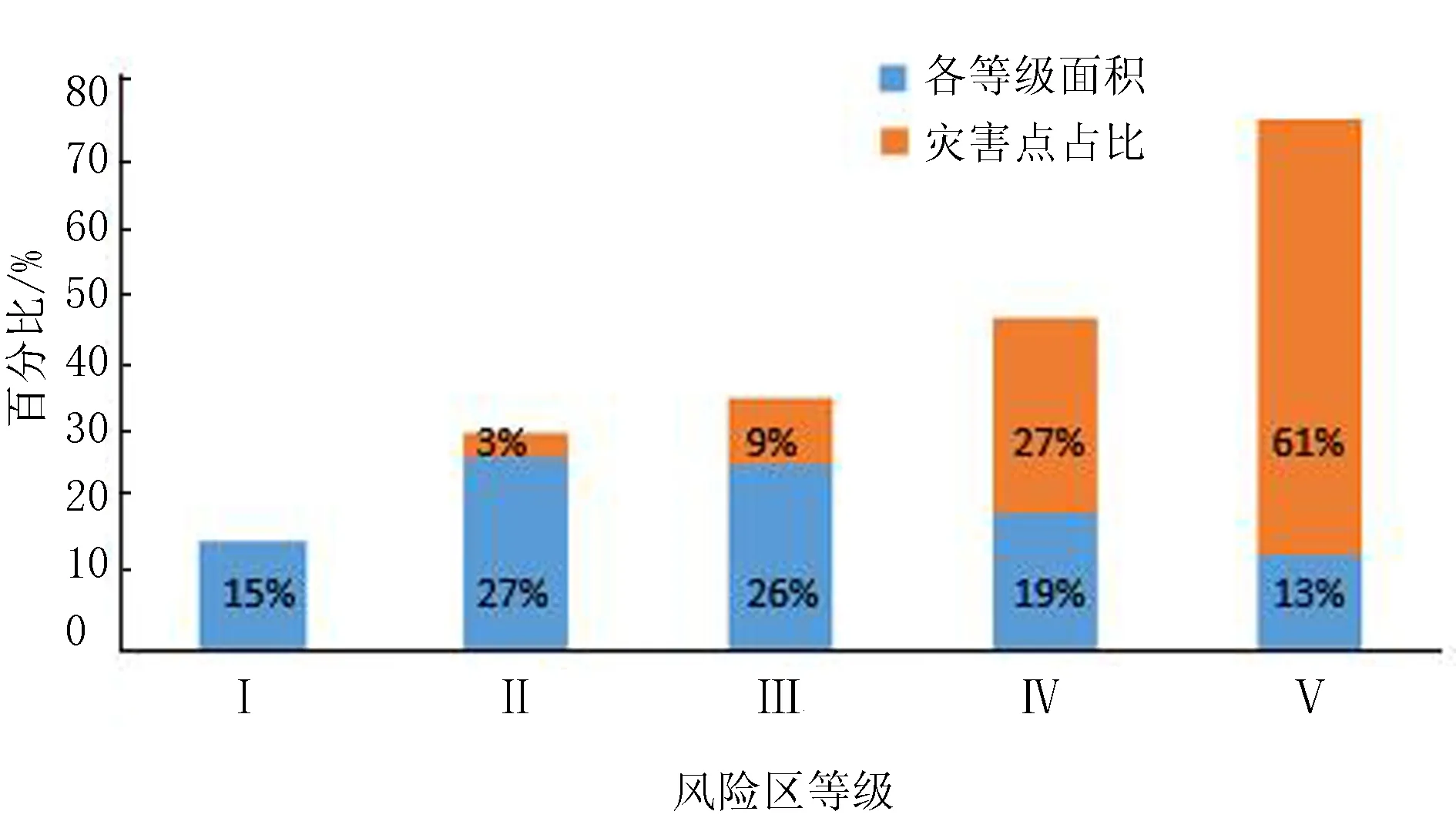
图13 各等级面积及灾害点占比

4.2 基于信息量模型的洪水灾害危险性评价

根据计算的信息量值，在图们江流域内，高程值为15～321 m，河网密度值为1.096～1.888 km/km2间，地形起伏度小于17 m，土地利用类型为耕地、草地或人造地表和裸地，处于一级缓冲区和二级缓冲区内时，这些影响因子的分级状态内信息量值比较大，即对洪水灾害的发生有比较大的贡献。

将由信息量法计算图们江流域洪水灾害评价图层进行风险等级划分，可得信息量法计算下图们江流域洪水灾害风险等级区划图(图14)。危险性较高的地区主要位于珲春市东部和南部、图们市南部、龙井市中部与延吉市南端接壤部分。

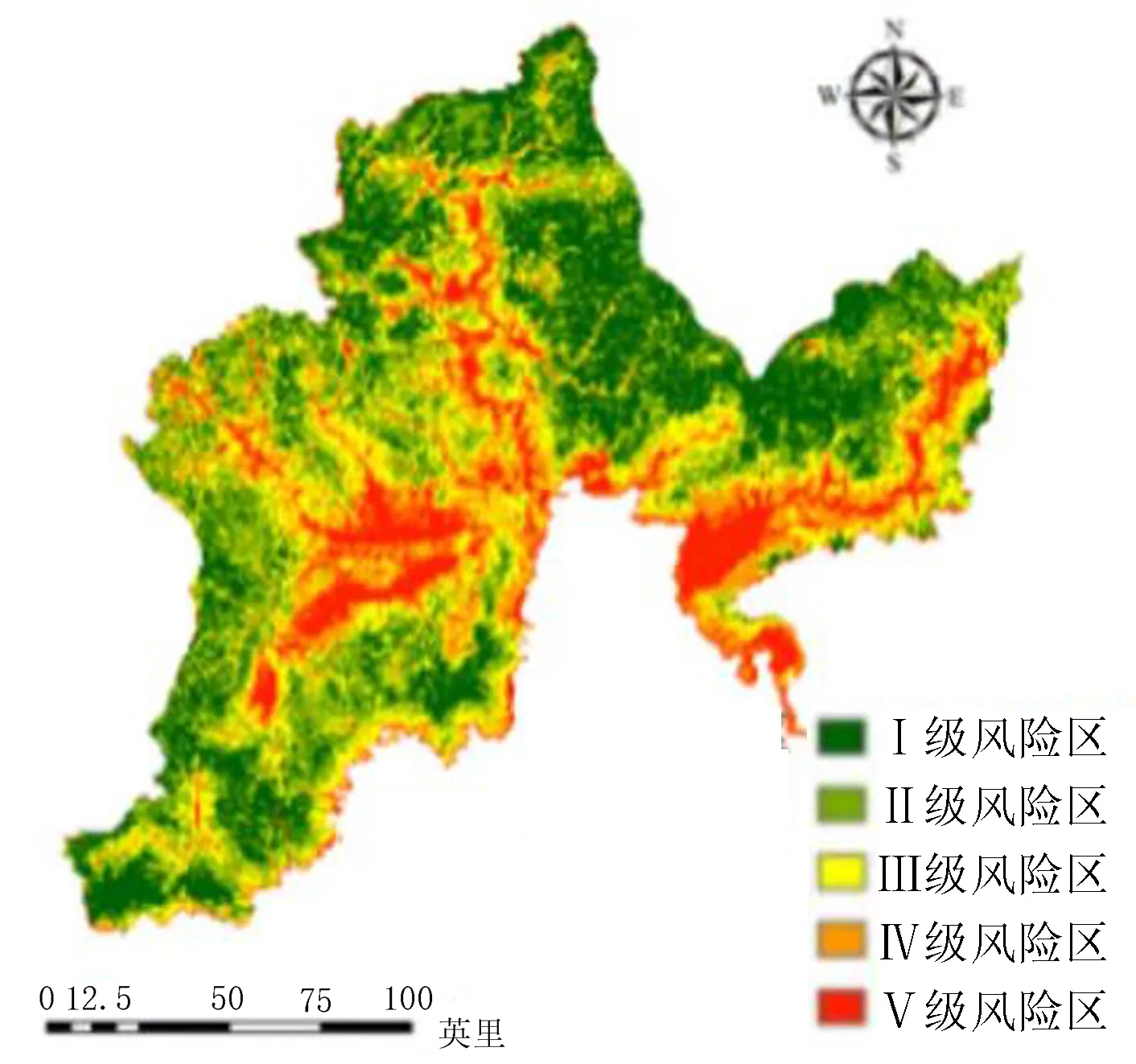
图14 基于信息量法的洪水灾害危险性区划图

由图15可以看出，Ⅰ～Ⅴ级风险区的面积分别为8 292、8 955.36、6 965.28、4 975.2和3 980.16 km2，占图们江流域总面积的比例分别为25%、27%、21%、15%和12%，在各风险区中灾害点的占比分别为0、3%、8%、19%和70%。该方法得出的最危险区域(V级)FR值为5.83。

图15 各等级面积及灾害点占比

4.3 基于随机森林模型的洪水灾害危险性评价

根据随机森林法计算得出权重构建的图们江流域洪水灾害评价模型(式4)并进行风险等级划分，可得随机森林法计算下图们江流域洪水灾害风险等级区划图(图16)。

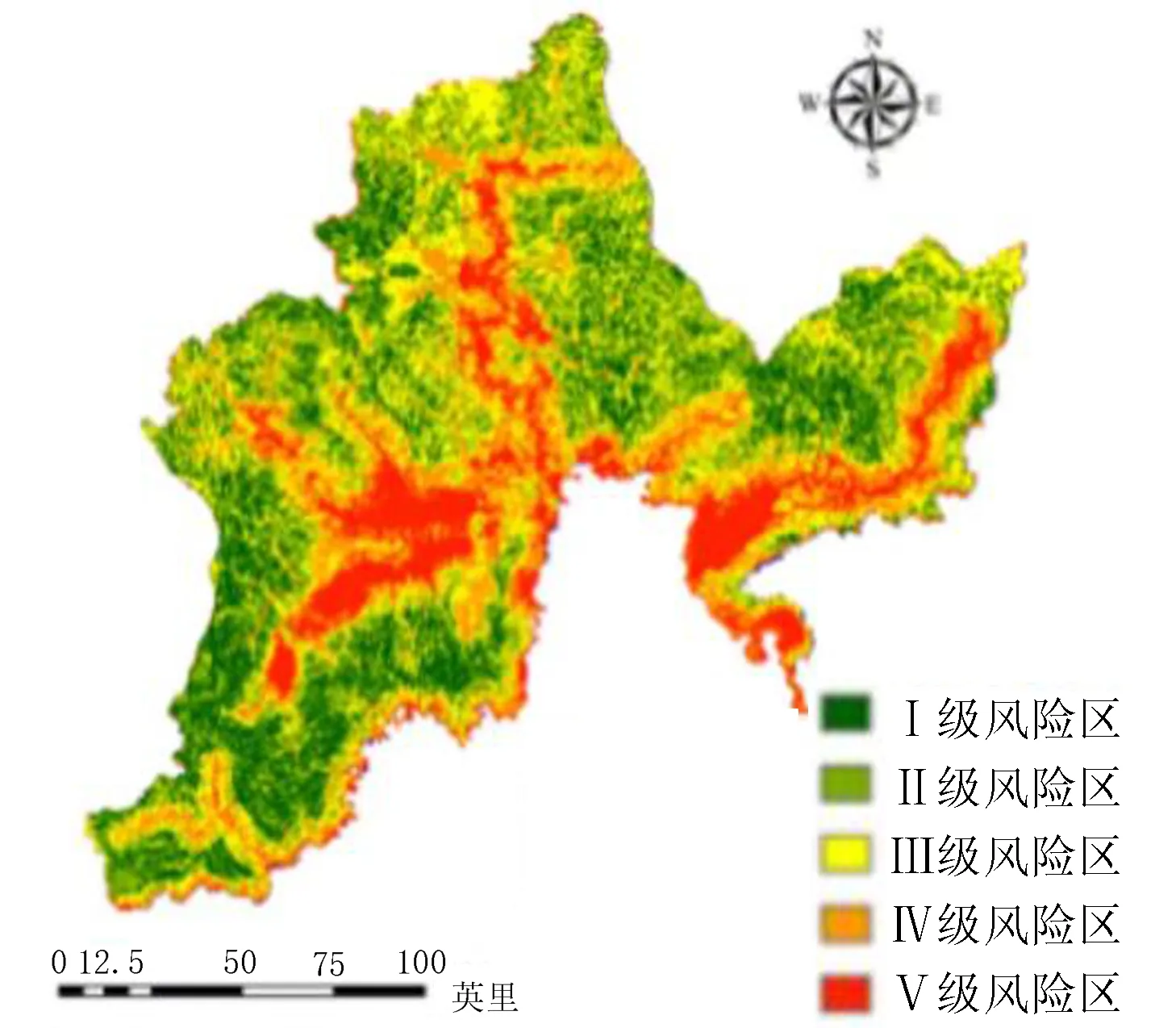
图16 基于随机森林法的洪水灾害危险性区划图Fig.16 Flood hazard zoning map based on the Random Forest Method

由图17可以看出,Ⅰ～Ⅴ级风险区的面积分别为5 638.56、8 292、8 623.68、6 301.92和4 311.84 km2，占图们江流域总面积的比例分别为17%、25%、26%、19%和13%，在对应风险区中洪水灾害点的占比分别为0、0、13%、22%和65%。该方法得出的最危险区域(V级)FR值为5。

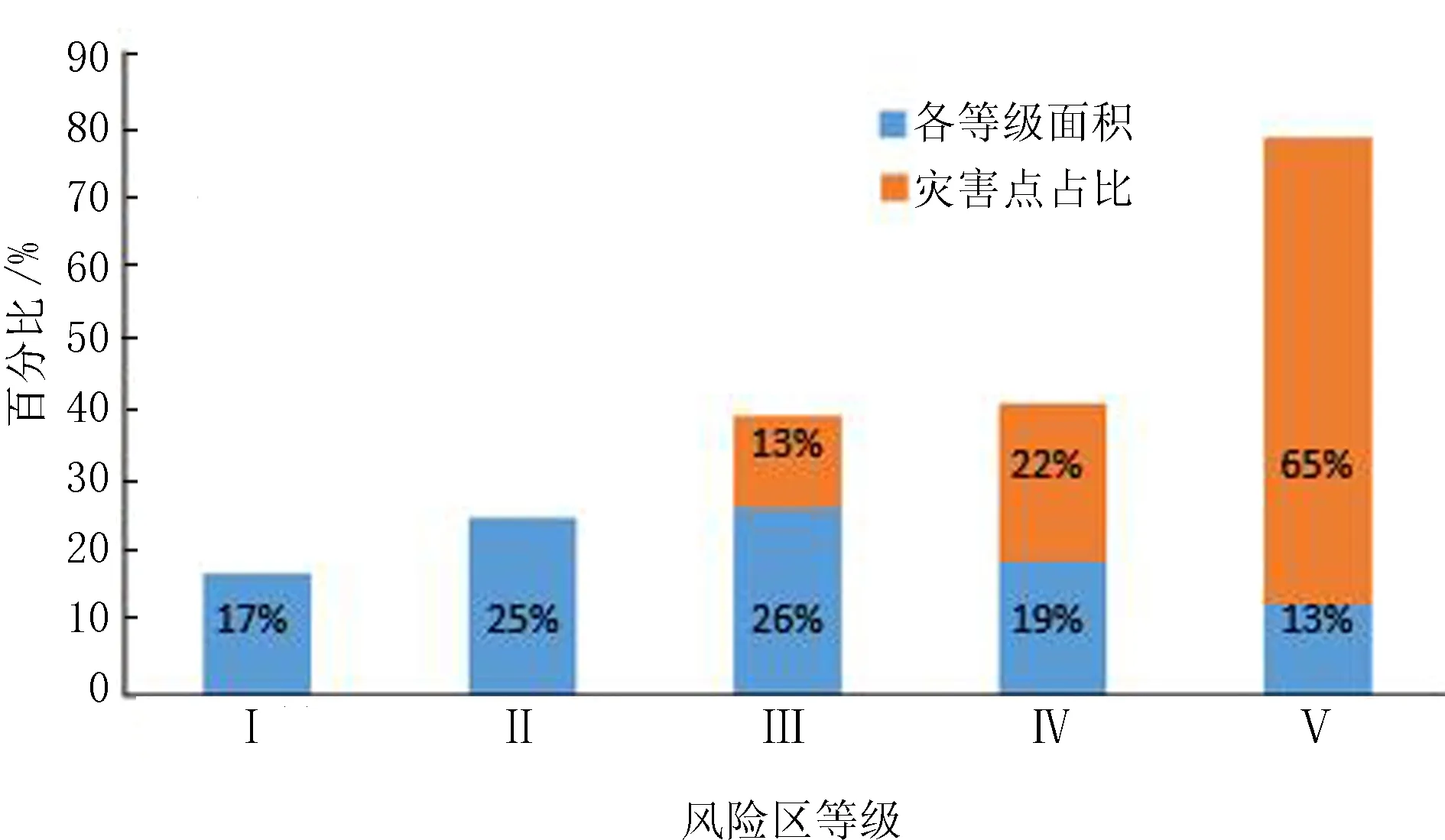
图17 各等级面积及灾害点占比

4.4 3种模型对比分析

根据以上结果可以看出在层次分析法计算下Ⅴ级风险区内灾害点占比为61%，信息量法计算下Ⅴ级风险区内灾害点占比为70%，而随机森林算法下则为65%。将3个图层在各级风险区下灾害点的占比进行对比分析(图18)，并用FR值做比较。

图18 不同算法下各级风险区灾害点占比

可以看出在Ⅴ级风险区中使用信息量法计算下的灾害点的占比是最高的，FR值为5.83，其次是随机森林算法计算，FR值为5，最后是层次分析法，FR值为4.69。综合Ⅳ级和Ⅴ级风险区内灾害点占比，可以看出信息量法计算下2个等级的风险区内灾害点占比和为89%，随机森林算法下占比和为87%，而层次分析法计算下占比和为88%。层次分析法计算下准确度低于其它2种算法的原因可能是其自身具备的主观性强于其它二者，在计算中没有用到灾害点本身具有的属性；随机数森林算法和信息量法各有所长，随机森林算法在低风险内的准确度较高，而信息量法在高风险区内的准确度较高，这2种算法都利用了洪水灾害点自身的属性特征来对未知的数据进行预测，科学性更好。将信息量法与随机森林算法计算下的图们江流域洪水灾害危险性预测图分别与选取的非灾害点的图层进行空间叠加，可以发现信息量法预测得到的图层更加符合非灾害点的分布情况，说明信息量模型对于图们江流域洪水灾害危险性的评价更为精准。

5 结论

该研究以图们江流域为研究区，设计了基于GIS和层次分析法、信息量法和随机森林算法3种算法的洪水灾害危险性判别试验，分别得到了不同算法下图们江流域洪水灾害危险性等级区划图和不同危险等级区内灾害点占比情况。结果显示，利用层次分析法、信息量法和随机森林算法获得的洪水灾害区划图中，最危险区域的面积分别为4 311.84，3 980.16和4 311.84 km2，每个区域中检测到的洪水灾害点的占比分别为61%、70%和65%。最终得出信息量模型对于图们江流域洪水灾害危险性的评价相较于层次分析模型和随机森林模型更为精准。在计算的信息量值中高程、河网密度、地形起伏度和河流缓冲区对洪水灾害贡献值较大。危险性较高的地区主要位于珲春市东部和南部、图们市南部、龙井市中部与延吉市南端接壤部分。其中高程、河网密度、地形起伏度和河流缓冲区对洪水灾害贡献的信息量值较大。根据图们江流域特点，该研究仅选择了8个因子进行研究，在今后的研究中可以通过分析更多影响因子和历史洪水灾害数据，提高洪水危险性评价精度，该研究成果对于洪水灾害风险管理、灾害预警和防治工作具有一定的科学和现实意义。