出租车收费问题探究*
张乐天 (江苏省苏州市阳山实验初级中学校初三(7)班 215151)
李沅骏 (江苏省苏州市阳山实验初级中学校初三(8)班 215151)
指导教师 孙 凯 (江苏省苏州市阳山实验初级中学校 215151)
1 问题背景
在我们的现实生活中处处存在着数学,可以说数学与现实生活密不可分.现实生活中的很多问题可以用数学知识来解决,这就要求我们在生活中要用数学的眼光观察生活现象,用数学的语言表达生活现象,尝试用数学知识、思想和方法探究生活现象中存在的某种数学关系,建立合适的数学模型来分析和求解实际问题.最近,我们注意到出租车这个重要的交通工具,对出租车收费问题产生了浓厚的兴趣.经过初步观察和思考,发现出租车收费是随着行驶路程的变化而变化的,若将出租车收费与行驶里程看成两个变量的话,当行驶里程确定时,出租车收费是唯一且确定的,从而我们可以判断出出租车收费与行驶里程之间是一种函数关系.那么出租车收费和其行驶里程之间存在什么样的函数关系?作为乘客,我们怎样乘坐出租车才能减少乘车费用支出呢?接下来我们围绕这些问题进行探究.
2 问题呈现
在苏州市范围内选取有代表性的出租车公司,拍摄了出租车收费标准(图1).已知出租车收费标准:行驶里程3 km内,起步费为10元;超过3 km,每1 km收费1.80元;超过5 km,单程加收50%空驶费.在调查研究的基础上,我们提出两个比较感兴趣的问题.

图1
问题1出租车收费与行驶里程间存在什么关系?
问题2乘客采用分乘两次的方法能降低乘坐出租车的费用吗?
3 分析问题
这是一个源于实际生活的问题.我们知道在现实生活中,出租车收费会受到各种因素影响,为了更好地开展问题探究,我们假设:(1)任意一辆出租车都按以上收费标准收费;(2)出租车匀速行驶; (3)行驶期间不堵车;(4)不考虑乘客主观乘车感受;(5)出租车驾驶员与乘客都认同收费标准; (6)不考虑行驶时间;(7)乘客单程乘坐出租车.
在作出以上假设之后,我们尝试用数学知识解决上面提出的两个问题.
4 建立模型
出租车收费是随着行驶里程的变化而变化的,不妨将行驶里程记为xkm,出租车收费记为y元,关于行驶里程,需根据实际情况进行分类.
(1)出租车收费标准中的“起步费10元(3 km内)”指的是行驶里程小于或等于3 km,实际上就是0 行驶里程0 (2)出租车收费标准中的“1.80/km”是指 3 km内起步费10元,超过3 km的里程部分按每1 km收1.80元的标准收费.此时行驶里程大于 3 km,考虑到标准中“超过5 km单程加收50%空驶费”,所以行驶里程应小于或等于5 km,即3 需要说明的是,当行驶里程不是整千米时,不足1 km的按1 km计算.根据以上分析,出租车收费应包括起步费和超过3 km部分的费用,用函数关系式表达为y=10+1.8(x-3),即y=1.8x+4.6.此时出租车收费y元与行驶里程xkm之间是一次函数的关系. 行驶里程3 (3)出租车收费标准中的“超出5 km加收50%空驶费”指行驶里程大于5 km时,超出 5 km的里程加收50%的空驶费,就是在每1 km收1.80元的基础上再加收50%,即每1 km收2.70元.这样,出租车收费包括三个部分:起步费+1.80/km收费+2.70/km收费.用函数关系式表达为y=10+1.8×2+2.7(x-5),即y=2.7x+0.1.此时出租车收费y元与行驶里程xkm之间也是一次函数的关系. 行驶里程x>5,收费y=2.7x+0.1. 综合以上三种可能的收费情况,得到出租车收费与行驶里程间的函数模型 我们建立了出租车收费与行驶里程间的函数模型,只要确定乘客的租乘里程就可以求得需支付的费用,提出的问题1也得以解决.我们知道行驶里程超过5 km要加收50%的空驶费,对于乘客而言,当行驶里程不超过5 km时是比较划算的,但很多时候乘客要到达目的地的里程超过 5 km甚至远远超过5 km,这个时候我们会想到一个问题:乘客采用分乘两次的方法能降低乘坐出租车的费用吗? 经过对实际问题的分析,建立数学模型并求解,我们获得结论:乘客采用分乘两次或多次的方法并不能降低租车的费用支出,在行驶里程较远的情况下,单次乘坐出租车仍然是相对最节省租车费用的方法. 教师点评将现实世界中的实际问题转化为数学问题,用数学知识、思想和方法解决问题的过程就是数学建模.张乐天、李沅骏两位同学能用数学的眼光观察生活,以出租车收费为研究对象,提出两个非常有价值的问题,用数学的语言呈现出清晰的数学问题,最后用数学的思维分析问题,建立函数模型并求解,完整体现了数学建模的活动过程,获得有价值的研究结论,非常值得大家学习借鉴.现实中的实际问题往往是错综复杂的、杂乱无序的、充满挑战性的,作为初中学生,敢于提出问题并用建立数学模型来求解,实属难得.希望更多的同学善于用数学的眼光观察生活,发现和提出有价值的问题,尝试建立数学模型求解,在问题的解决中体悟数学的应用价值.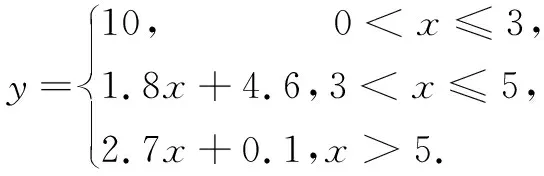
5 解决问题
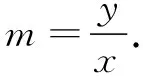
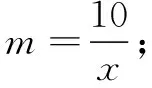
6 研究结论

