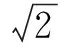萃取数学史 建构概念课
——以苏科版八上“平方根”为例*
魏宇亭 (江苏省邳州市戴庄中学 221347)
1972年第二届国际数学教育大会(ICME-2)在英国举行,会上组建了“数学史与数学教学之关系国际研究小组”(简称为HPM).该组织成立后,致力于数学史在数学教学中的应用研究,如美国数学史专家福韦尔指出数学史具有可增加学生的学习动机,有助于学生理解概念等教育价值;美国学者琼斯认为用数学史进行新课引入可以帮助学生“发现”新概念或新思想方法.史宁中、孔凡哲教授也指出,数学是人类文化的重要组成部分,数学教育是数学文化的教育,而数学史是数学文化的一种载体,数学史融入数学课程有助于学生理解数学.[1]基于上述理论,笔者在徐州市级同课异构活动中,通过萃取数学史建构概念课,执教了苏科版八上“4.1平方根”一课,得到与会师生的好评.
1 教材分析
1.1 基于知识链的教材分析
本课是苏科版数学八上(以下简称为教材)第四章第1节.七年级时,学生已学习了有理数的加、减、乘、除、乘方等运算,能识别简单的无理数.本学期,学生已学习勾股定理,经历了运用平方求直角三角形边长的过程,奠定了学习平方根的基础.本章将学习实数的概念,八下将学习二次根式,九上将学习解一元二次方程.因此,平方根是重要的概念枢纽,发挥承前启后的作用,体现课标对重要数学概念螺旋式上升的要求.据此,可绘如图1所示的结构图.
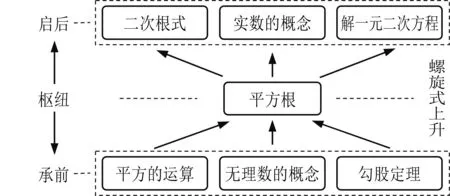
图1
1.2 基于数学史的教材分析
·蕴藏勾股定理的历史背景
本课教材中设计了如图2的引图,要求学生在边长为1的网格中求AB,A′B′的长,虽然AB,A′B′是矩形的对角线,但实质是运用勾股定理求解,图形上略显复杂,会给部分学生带来识图困难.因此,抓住勾股定理这一线索,依据HPM的理念,萃取毕达哥拉斯发现勾股定理后提出万物皆数的数学史,直接创设求直角三角形边长的情境,剑指学习平方根的必要性,既可达成引图的目标,又能解决识图困难,让学生在传承有序、自然而然的数学史情境中建立新概念.
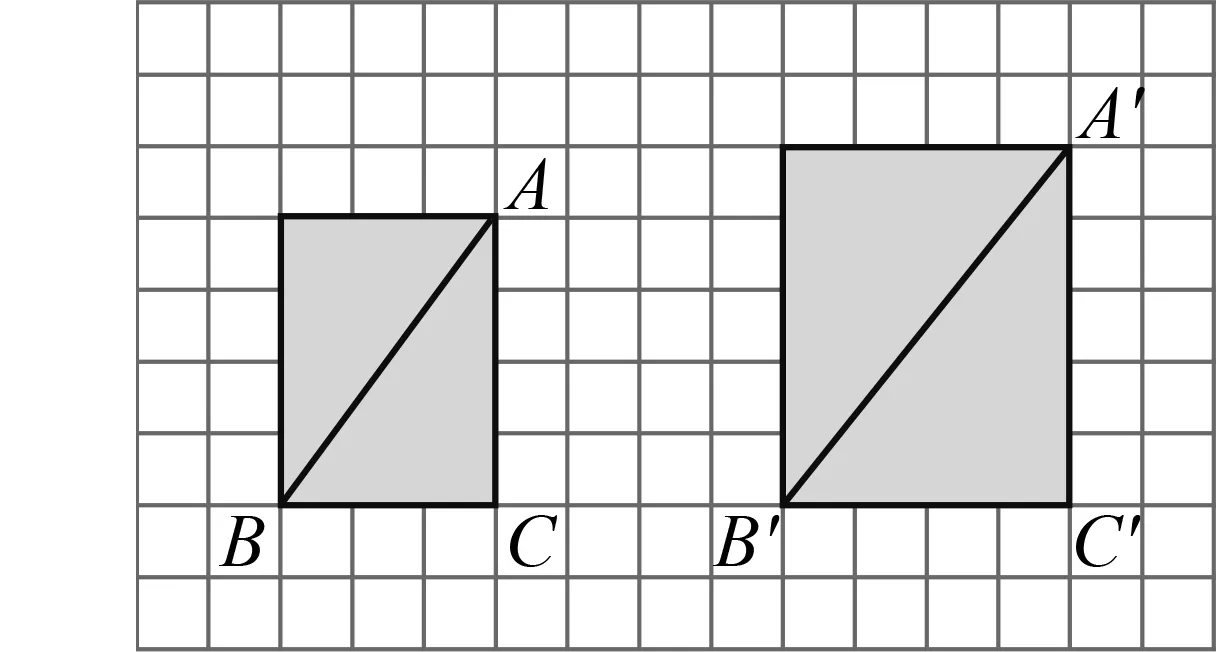
图2
·蕴藏发现无理数的历史背景
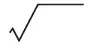
2 教学设计
2.1 跨越时空,引出概念
(1)出示图3,回顾邮票的图案是根据勾股定理设计的.

图3 图4
(2)出示图4,数学史:在西方,勾股定理被称为“毕达哥拉斯定理”,它是古希腊数学家毕达哥拉斯发现的.毕达哥拉斯发现勾股定理后,试着从数学扩大到哲学,用数的观点解释世界,经过刻苦实践,提出了“万物皆数”的观点,这里的数是指一个精确的数字,随后逐渐形成毕达哥拉斯学派.
(3)出示图5,求直角三角形第三边长,经历运算过程,体验“万物皆数”的观点.
(4)出示图6,数学史:希帕索斯是毕达哥拉斯学派中一个聪明、好学、有独立思考能力的青年数学家,他在研究勾股定理时,发现了一个大问题.
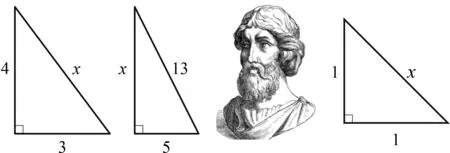
图5 图6 图7
(5)出示图7,求腰长为1的等腰直角三角形的斜边长,用逼近法,感受斜边的数值特征.
(6)数学史:希帕索斯的发现,打破了毕达哥拉斯万物皆数的权威,史称“第一次数学危机”.他坚持真理,并付出了生命的代价.后世数学家在此基础上定义了新数字,开创了新运算.
设计意图萃取与毕达哥拉斯和希帕索斯相关的数学史创设情境,在求等腰直角三角形斜边的问题中,让学生感受无理数的客观存在性、数字扩充的现实性、开创运算的必要性,为建构概念奠定思维基础,用希帕索斯宁死求真的故事对学生进行情感、态度、价值观的教育,发挥学科育人功效.
2.2 抽象本质,生成概念
·建立互逆,感悟特征
(1)出示图8左侧3题,快速求解.
(2)追问:请举出相同的例子,有何发现?
(3)出示图8右侧3题,学生思考后,指名回答.

图8
(4)追问:你有什么发现?
设计意图建立互逆关系,使学生感悟运算的互逆性及已知幂和指数求底数的运算特征.
·追问促思,生成概念
(1)指名回答,组织讨论,统一意见.
若x2=0,则x=;若x2=-4,则x=.
(2)抽象本质,逐步建构,生成概念.若用字母a表示等号右边的数字,则可表述为:如果x2=a(a≥0),那么x叫做a的平方根.
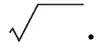
(3)追问:若x2=2,则x=.
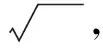
2.3 列表归类,探究概念
(1)整理下表,设问:观察表格,你发现了什么规律?

a9140.1620-4a的平方根±3±12±0.4±20无
(2)学生思考,小组合作,发表意见.
(3)小结:一个正数有两个平方根,它们互为相反数;0的平方根是0;负数没有平方根.
(4)开平方的定义:求一个数的平方根的运算叫开平方.
2.4 例题教学,运用概念
(2)先出示①至③,指名回答;再依次出示④至⑥,讨论完成.
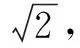
2.5 辨析巩固,深化概念
(1)判断下列说法是否正确:① -5是25的平方根;② 25的平方根是-5;③ 0的平方根是0;④ 1的平方根是1;⑤ (-3)2的平方根是-3.
(2)学生在独立思考、小组讨论后完成辨析.
设计意图辨析讨论,学生进一步感悟平方根的概念和性质.
2.6 课堂小结,升华概念(略)
2.7 沙场点兵,巩固概念
组织学生以抢答的形式,解答习题.
(1) 4的平方根是( ).
A.16 B.±4 C.±2 D.8
(2)如果1.2是a的平方根,那么另一个平方根是.
(3)一个实数的平方根是a+3和2a,则a=.
2.8 板书设计
本节课的板书设计如图9所示.
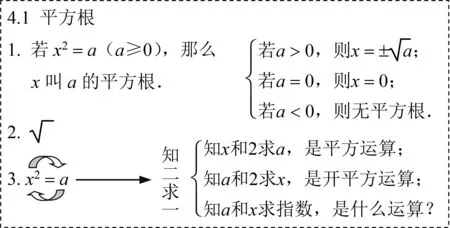
图9
3 教学反思
3.1 萃取数学史,创设产生概念的模拟情境
3.2 萃取数学史,建构概念体系的知识链条

3.3 萃取数学史,在概念教学中渗透“三会”