基于层次贝叶斯法的高山松生物量估测模型

黄金君， 舒清态， 席 磊， 孙 杨， 刘玥伶

( 1.广西壮族自治区中国科学院广西植物研究所，广西桂林541006；2.西南林业大学林学院，云南昆明650224)

森林地上生物量(AGB)作为森林生态系统能量交汇以及生态健康功能评价的重要指标，对全球陆地与大气间的碳物质平衡影响巨大。根据《2019年中国国土绿化状况公报》，中国森林覆盖率已达到22.96%(2019年6月17日)，相比于全国第8次森林资源清查的覆盖率提高了1.33个百分点。加强对乔木林不同器官生物量的研究，获得更加精准的森林地上生物量数据，对于深入研究森林生态系统生产力以及揭示陆地生态系统结构与生态环境的关系具有重要的科学与现实价值[1-2]。当前国内外估测森林地上生物量的方法主要基于森林资源清查法与基于遥感估测法，基于森林资源清查法是指利用高密度样地调查获得的数据建立不同树种异速生物量模型，进而估算不同尺度的森林地上生物量[3]。异速生物量模型通过将易测的胸径或树高等指标相结合以提供一种高效简单的估算生物量方法，目前已被广泛应用[4-5]。然而使用传统方法拟合异速生物量模型存在过多局限，其只将模型参数视作固定变量，未能综合考虑存在的多种生物或非生物因素[6-7]。因此选用层次贝叶斯方法有助于解决这一问题，其利用概率分布描述模型中的未知变量，并将样本信息与参量视作随机变量[8]。在当前精准提升森林质量的背景下，贝叶斯方法正逐渐成为林业领域中学者们研究的热点。Green等[9]于1992年首次在林业应用中引入层次贝叶斯方法，并于1996年建立了基于种植园杉木的贝叶斯模型[10]。Clark等[11]于2007年使用贝叶斯方法建立了树木直径生长模型，Metcalf等[12]于2009年建立了基于非参数贝叶斯法的树木死亡率模型，张雄清等[13]于2014年建立了基于贝叶斯法的杉木人工林树高增长模型，王冬至等[14]于2019年建立了基于贝叶斯法的针阔混交林树高与胸径混合效应模型，姚丹丹等[15]于2020年建立了基于贝叶斯法的蒙古栎林单木树高-胸径模型。已有研究结果表明，利用贝叶斯方法可以有效提高模型估测精度与可靠程度。层次贝叶斯法基于贝叶斯理论发展，通过分离不同层面中多个参数的复杂关系，从而充分发挥具有层次结构模型的优势。本研究以高山松天然林为研究对象，以区域为分层单位，分别采用层次贝叶斯法与非层次贝叶斯法构建高精度单木及不同组分生物量估测模型，探讨贝叶斯方法在单木及不同组分生物量估测模型中的运用。

1 材料与方法

1.1 研究区概况

以云南省香格里拉市小中甸镇和洛吉乡的高山松天然林为研究对象。小中甸镇地理坐标为99°36′～99°59′E，27°20′～27°43′N，地处香格里拉市南部高寒坝区，多年平均气温5.8 ℃，森林覆盖度69.42%，主要乔木树种包括高山松(PinusdensataMast)、云杉(PiceaasperataMast)、冷杉[Abiesfabri(Mast.)Craib]、落叶松[LarixgmelinⅡ (Rupr.) Kuzen]等。洛吉乡地理坐标为99°55′～100°19′E，27°38′～28°06′N，地处香格里拉市东部，海拔差异悬殊大，南部河谷区最低点海拔为1 503 m，北部高寒山区最高点海拔为4 495 m，南部河谷区年平均气温为13～15 ℃，北部高寒山区年平均气温为5.5 ℃，森林覆盖度为78%，主要乔木树种有高山松(PinusdensataMast)、云南松(PinusyunnanensisFranch)、冷杉[Abiesfabri(Mast.)Craib]、云杉(PiceaasperataMast)、落叶松[LarixgmelinⅡ (Rupr.) Kuzen]、核桃(JuglansregiaL.)等。将在小中甸镇和洛吉乡采集到的数据分为区域Ⅰ和区域Ⅱ，基本数据信息如表1所示。2个区域高山松的胸径和树高数据包含区域间与样地间的嵌套关系，即分层数据[16]。数据分为2层，第1层是地域空间的胸径和树高数据，第2层为每个地域空间内样本的胸径和树高数据。通过对研究区样本数据进行方差分析可知，单木样本数据之间存在显著的地域性差异。

表1 高山松基本数据信息

1.2 数据来源

分别在2个区域内同一森林类型的林分中设置56块面积为30 m×30 m的高山松天然纯林标准样地，记录样地的中心点经纬度坐标、海拔、坡度和坡向等空间位置信息，郁闭度、林龄和龄级等测树学因子。最后于每块样地中随机选择1～3株具有代表性的高山松单木，伐倒后测定其生物学特性。伐倒样木共计115株，包括区域Ⅰ的60株样木和区域Ⅱ的55株样木，每株高山松的数据被分成单木生物量、树干生物量、木材生物量、树皮生物量、树枝生物量、树冠生物量和树叶生物量7个组分来分别进行测定。树干生物量主要采用材积密度法测量，枝、叶生物量采用分级标准枝法测量。最后分别取样称量，烘干处理后计算单木生物量及各器官的生物量(表2)。

表2 单木及不同组分的高山松生物量数据

1.3 异速生物量模型的建立

异速生长方程反映了树木各维量间按比例变化协调增长的关系，具有广泛的适应性、较高的灵活性和良好的拟合性等特性，因此该方程在森林生物量估算中被广泛应用[17-18]。模型表达式为：

G=aDbHc

(1)

式中：G代表高山松单木及不同组分的生物量，D代表胸径，H代表树高，a、b、c代表高山松单木及不同组分生物量模型的异速生长参数。

1.4 研究方法

1.4.1 非层次贝叶斯法 随着马尔科夫链蒙特卡洛(MCMC)方法的逐渐成熟，贝叶斯方法在多个领域的研究与应用越来越广泛[19-20]。与经典统计学方法相比，贝叶斯方法包含1个最为重要的要素(参数的先验信息)，该方法通过在已有知识的基础上推测出新的信息，即得到所求模型参数的后验分布。经典统计学方法将未知参数视作固定变量，只考虑样本与整体信息，而贝叶斯方法综合考虑样本信息、整体信息及先验信息，并使用概率分布描述模型的未知参数。在未进行样本数据抽样时，研究人员根据已有的文献资料或经典统计学方法得到模型参数ϑ的信息(如均值与方差)，且设定了1个概率分布R(ϑ)来描述该信息的随机性，此分布则成为参数ϑ的先验分布。将本研究的高山松样本数据设为M=(M1，…，Mn)，似然函数为L(M|ϑ)，后验分布R(ϑ|M)则是建立在先验分布R(ϑ)与似然函数的基础上，样本数据的边缘概率密度分布为ʃL(M|ϑ)R(ϑ)dϑ，最后由贝叶斯公式对先验分布、似然函数以及后验分布进行组合，计算公式如下：

(2)

1.4.2 层次贝叶斯法 层次贝叶斯法作为现代贝叶斯方法中极为典型的代表，通过对不同层次上多个参数间的复杂关系进行分离，解决了普通贝叶斯法对于复杂参数分布估计的困难[21]。与普通贝叶斯法相比，层次贝叶斯法允许不同的参数出现在不同层面上，且采用了分层先验信息，有助于消除先验信息对模型估计结果的过度影响，分层先验的表达公式如下：

R(ϑ)=ʃR1(ϑ|τ)R2(τ)dτ

(3)

首先对未知参数ϑ设定1个已知先验分布ϑ～R1(ϑ|τ)，当给定的先验分布中超参数τ难以确定时，再给出1个超先验R2(τ)，因此由先验与超先验共同构成新的先验，称为分层先验。由参数ϑ和超参数τ组成的后验分布函数为：

R(ϑ,τ|M)∝R(M|ϑ,τ)R1(ϑ|τ)R2(τ)

(4)

在本研究中不仅采用分层先验信息，同时还对数据进行了分层。假设样本数据被分成K组，即把单木及不同组分生物量的数据分成了I区和Ⅱ区，样本观测值Mij(i=1，2，3，…，K；j=1，2，3，…，Ni)代表第i组中第j个样本观测值，I区和Ⅱ区之间样本观测值差异较大，每个组内的样本观测值差异较小。

1.4.3 先验信息 贝叶斯方法中丰富的先验信息影响着模型参数的估计，需要为所求参数构造适当的先验分布。有些研究人员建议采用无信息先验，无信息先验通常出现在方差无穷大与均值为0的高斯分布中，对参数不会造成太大的影响。也可采用有信息先验(Informative prior)作为贝叶斯方法的先验分布信息，其来源于统计学方法计算得到的数据或前人的研究成果等[22]。本研究采用非线性最小二乘法的估计结果作为非层次贝叶斯法与层次贝叶斯法的先验信息[23]。

1.5 软件处理

使用OpenBUGS软件[24]实现层次贝叶斯法与非层次贝叶斯法的模型参数估计。OpenBUGS软件以MCMC方法为基础，通过Gibbs和Metropolis算法从参数的后验分布中抽样，从而完成马尔科夫链的迭代以及参数的估计，极大促进了贝叶斯方法的应用。

1.6 模型精度评价方法

采用十折交叉验证方法，将高山松样本数据集分成10份，轮流将数据集中的9份作为训练数据，剩下的1份作为测试数据。通过选用决定系数(R2)、均方根误差(RMSE)和平均绝对误差(MAD)3个指标，对层次贝叶斯法与非层次贝叶斯法拟合不同组分异速生物量模型的精度进行评价，每个指标的计算公式如下：

(5)

(6)

(7)

2 结果与分析

2.1 基于非层次贝叶斯法的参数估计结果分析

采用非层次贝叶斯法对高山松单木及不同组分异速生物量模型[公式(1)]进行拟合，发现模型R2均较高(树叶生物量模型除外)且存在极显著差异(P<0.01)，表明该方法适合该方程的拟合。为获得准确的异速生长后验参数估计值，本研究最开始设置1 000次抽样以消除初始值对抽样的影响，待模型参数拟合稳定后迭代次数设为10 000次。迭代完成后便可得到非层次贝叶斯法中各个器官异速生长参数的均值、标准差和95%置信区间。如表3所示，异速生长参数a的标准差和95%置信区间范围<异速生长参数b的标准差和95%置信区间范围<异速生长参数c的标准差和95%置信区间范围，说明异速生长参数a的估计值在模型抽样迭代过程中比参数b和参数c更稳定。

表3 基于非层次贝叶斯法的单木及不同组分生物量模型参数估计结果

2.2 基于层次贝叶斯法的参数估计结果分析

使用非线性最小二乘法的估计结果作为先验信息，以区域进行分层，采用层次贝叶斯法对高山松单木及不同组分异速生物量模型[公式(1)]进行拟合，发现模型R2均较高(树叶生物量模型除外)且存在极显著差异(P<0.01)，表明该方法适合该方程的拟合。为获得最优的模型参数后验估计值，本研究共设置11 000次迭代，得到层次贝叶斯法I区和Ⅱ区中各个器官异速生长参数的均值、标准差和95%置信区间。层次贝叶斯法的参数估计结果如表4所示，可见Ⅰ区和Ⅱ区中各个器官异速生物量模型均有不同的异速生长参数，且参数的均值差异较大，说明不同区域中各个器官的生物量存在差异。异速生长参数a的标准差和95%置信区间范围整体上小于异速生长参数b和c，与非层次贝叶斯法的估计结果一致。

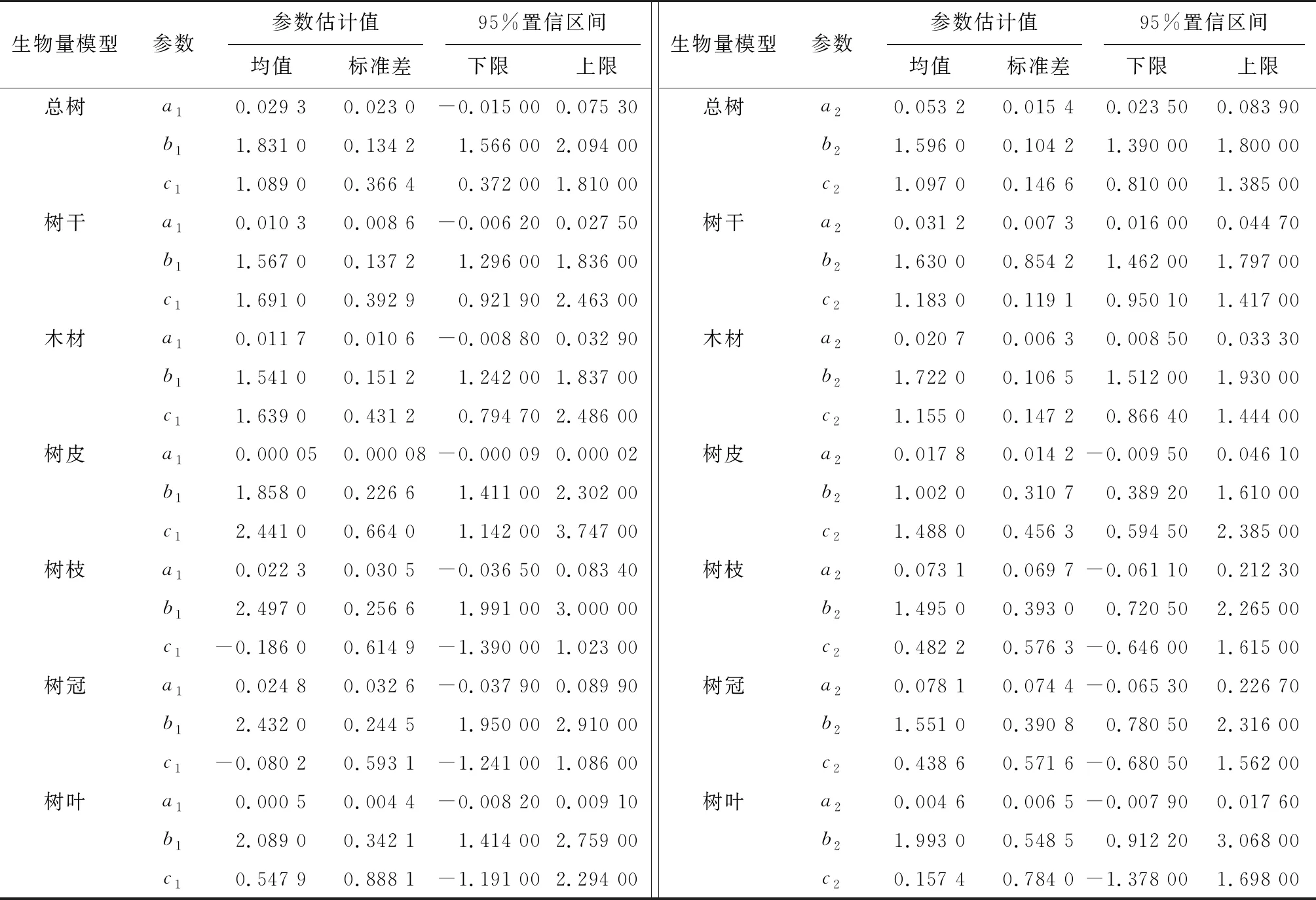
表4 基于层次贝叶斯法的单木及不同组分生物量模型参数估计结果

2.3 不同方法拟合高山松异速生物量模型的精度对比分析

用层次贝叶斯法与非层次贝叶斯法拟合高山松不同组分异速生物量模型的结果(表5)显示，这2种方法的决定系数(R2)、均方根误差(RMSE)和平均绝对误差(MAD)呈现的规律一致：树干生物量、木材生物量和单木生物量模型效果最优，树皮生物量、树冠生物量和树枝生物量模型效果较优，树叶生物量模型效果较差，层次贝叶斯法拟合模型的R2区间为[0.365 0,0.965 0]，非层次贝叶斯法拟合模型的R2区间为[0.437 0,0.964 7]。通过对比层次贝叶斯法与非层次贝叶斯法拟合模型的效果发现，层次贝叶斯法拟合模型的效果更好(树枝与树叶生物量模型除外)，用该法拟合的单木生物量、树干生物量、木材生物量、树皮生物量和树冠生物量模型的R2分别较非层次贝叶斯法提高了0.012 0、0.000 3、0.000 1、0.006 5、0.005 6，RMSE分别降低了8.94 kg、0.28 kg、0.03 kg、0.30 kg、0.27 kg，MAD分别降低了3.31 kg、0.11 kg、0.42 kg、0.03 kg、0.30 kg。

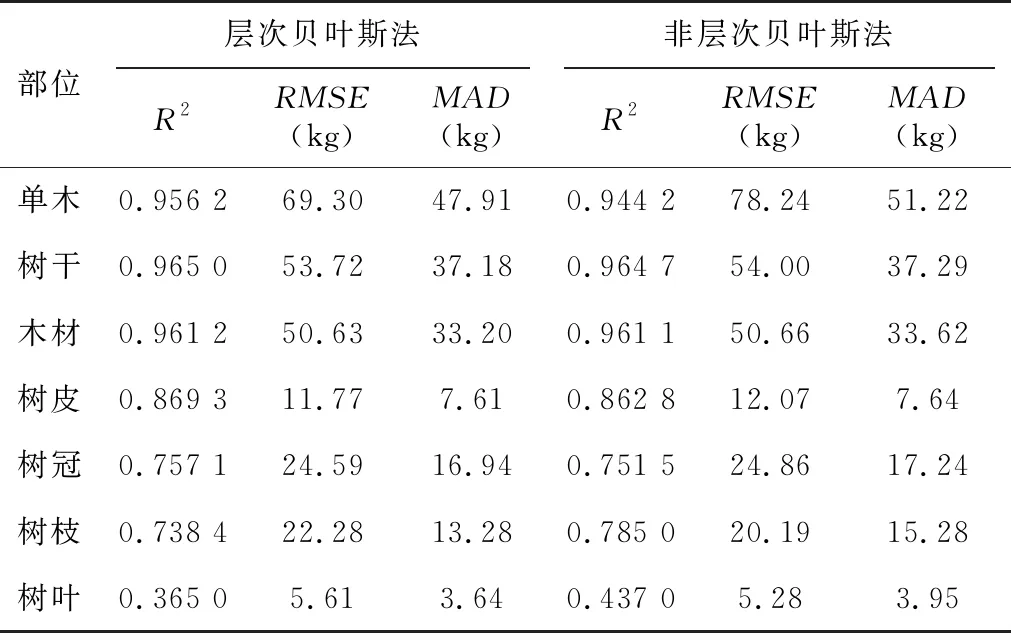
表5 基于单木及不同组分异速生物量模型的不同方法精度结果对比

3 讨论与结论

本研究主要探讨了贝叶斯方法在异速生物量模型中的应用，选取香格里拉市Ⅰ区和Ⅱ区共115株高山松单木进行解析，每株高山松的数据被分成单木生物量、树干生物量、木材生物量、树皮生物量、树冠生物量、树枝生物量和树叶生物量7个组分来进行测定，重点分析了层次贝叶斯法与非层次贝叶斯法拟合不同组分异速生物量模型中存在的差异，证实不同区域对生物量产生了重要的影响。

贝叶斯方法的一个优势在于使用马尔科夫链判断模型参数的平稳分布与收敛，而经典统计学方法使用样本的渐进方差来判定，无法考虑样本数据中包含的不确定信息。在使用贝叶斯方法拟合不同组分异速生物量模型的过程中，除了树枝与树叶生物量模型，层次贝叶斯法的拟合效果整体优于非层次贝叶斯法。该结果一方面说明了层次贝叶斯法有助于提高生物量模型的估测精度与准确度，另一方面说明，树枝与树叶生物量占总树生物量的比例较小，所含有的不确定性因素较少[25]，因此使用非层次贝叶斯法效果更好。层次贝叶斯法适合分析包含多种不确定性因素的复杂数据，通过综合考虑多层面的各种因素以及将模型中的参数看作随机变量，来展现不同组间样本数据的异质性与同一组内不同样本数据的相异性，从而提高建模的灵活性和准确性。姚丹丹等[26]使用层次贝叶斯法、贝叶斯法和非线性最小二乘法拟合蒙古栎林单木枯死模型，发现层次贝叶斯方法的模型结果最好。黄兴召等[27]使用层次贝叶斯法拟合安徽省马鬃岭林场和福建省东安林场杉木的生物量转换因子函数时，发现设置区域为随机效应有助于提高模型精度，层次贝叶斯法可以解决区域对于某一类型森林生物量的影响。

本研究采用层次贝叶斯法与非层次贝叶斯法拟合了高山松单木及不同组分的异速生物量模型，提供了1种在区域层面上估计高山松生物量的有效方法。通过分析2种方法的精度发现，层次贝叶斯法拟合的单木生物量、树干生物量、木材生物量、树皮生物量和树冠生物量模型的R2分别较非层次贝叶斯法提高了0.012 0、0.000 3、0.000 1、0.006 5、0.005 6，RMSE分别降低了8.94 kg、0.28 kg、0.03 kg、0.30 kg、0.27 kg，MAD分别降低了3.31 kg、0.11 kg、0.42 kg、0.03 kg、0.30 kg。通过对比2种方法对不同组分生物量模型拟合的效果发现，树干生物量、木材生物量和单木生物量模型的效果最优，树皮生物量、树冠生物量和树枝生物量模型的效果较优，树叶生物量模型的效果较差。综上所述，层次贝叶斯法可以有效地提高模型估测精度，且更适合分析在复杂环境中受多因素影响的数据，加强层次贝叶斯法在林业领域中的研究，将具有较大的参考意义。