梯度纳米结构多晶铝剪切变形的分子动力学模拟
黄倩如,刘江辉,孔毅,杜勇
(中南大学 粉末冶金国家重点实验室,长沙 410083)
多晶结构沿某一方向的空间分布存在梯度时会导致局部或整体材料性能的变化,这是因为结构梯度的引入有时可引入独特的塑形变形机制,从而克服传统材料中强度与韧性的约束,缓解应力集中,从而使得力学性能增强[1-2]。2015年,卢柯等[3]系统总结了铜基和钢等梯度纳米结构材料实验方面的研究进展。卢柯等[4]采用表面纳米化的方法制备具有梯度晶粒尺寸分布的Cu,从表面到内部,晶粒尺寸从20 nm线性增加至300 nm,屈服强度达到130 MPa,为粗晶铜的2倍,同时表现出和粗晶铜相同的延展性。LEE等[5]采用低温球磨后热等静压的方法制备了3组具有双峰值晶粒尺寸的Al-7.5%Mg合金,粗晶占比分别为0、15%和30%。这3组合金的屈服强度较5083铝提高约4倍,特别是粗晶占比为 30%的合金,抗拉强度达到 700 MPa,比完全纳米晶合金的抗拉强度(850 MPa)仅降低17%,但延展性提高近3倍,有非常明显的提升。
铝及其合金作为一类轻质材料,兼具高比强度、良好的导热性能、较强的耐腐蚀性能与装饰性能,以及优异的切削加工性,且节能环保[6-7],在汽车、船舶、航空航天、建筑、轻工业等多个领域得到广泛应用[8-9],但现代社会的发展对铝合金的力学性能在内的各项性能都提出了更高的要求[10]。以往人们更多地关注Mg、Si、Cu、Fe、Zn、Cr等添加元素对铝及其合金性能的影响[6],将这些元素加入到纯铝中形成铝基固溶体,使得晶格发生畸变,增加位错运动的阻力[11-12],提高铝合金的强度,但提升范围有限,且会造成一定程度的塑性损失。近些年,研究人员发现对微观组织进行调控同样也能起到优化铝及其合金性能的作用[13-14]。比如:经高压扭转(high pressure torsion, HPT)处理而获得的超细晶Al-4.1Mg合金,强度高达约800 MPa[6];1570铝合金在大塑性变形加工纳米晶化后,屈服强度达到950 MPa,且伸长率达到4.7%[14];经HPT处理的超细晶 7475铝基合金在保持较高强度的同时具有高延展性[15]。有研究表明:具备梯度纳米结构,即晶粒尺寸呈现一定梯度的连续变化的材料,能够兼具高塑性、高强度与优良的抗疲劳性能。分子动力学作为一种原子尺度的计算模拟方法,可考察与分析模拟体系中各粒子的运动状态,进而对体系的物理性质进行研究[16]。ZHOU等[17]运用分子动力学研究梯度纳米晶粒(gradient nano-grained, GNG)铜膜的塑性变形,发现由于不同粒度层之间的相互协同作用,随应变量不断增加,发生由小晶粒逐渐传播到较大晶粒的有序塑性变形,GNG 薄膜中明显抑制了由变形引起的晶粒粗化,并最终出现额外强化。本文作者拟构筑具有不同梯度纳米结构的多晶铝原子结构模型,运用分子动力学方法对其进行结构弛豫与剪切变形的计算模拟,探讨梯度纳米结构对其力学性能的影响,研究在同一变形条件下大小晶粒的形变机制和剪切变形过程中微观结构的变化。
1 计算方法
本文主要采用Voronoi方法[18]来构建梯度纳米结构的多晶铝模型。为了实现晶粒尺寸在三维空间上的梯度分布,将4 nm×4 nm×16 nm的模拟盒子,沿长轴方向(Z轴方向)16 nm长度内从上到下分为多个相同大小的区域,在不同区域内依次随机生成不同个数的晶粒核心,进而基于Voronoi方法[18]生成沿Z轴方向晶粒尺寸呈现梯度分布的梯度纳米多晶结构,再运用公共近邻分析(common neighbor analysis,CNA)方法[19]对不同结构的原子进行着色,得到如图1(a)所示的梯度纳米多晶铝结构1的结构示意图。从图中看出,晶粒尺寸沿Z轴自上而下逐渐变小。运用相同方法构建不同形貌与结构梯度的结构2、结构3与结构4(如图1(b),(c)与(d)所示),以便于后续进行不同梯度结构的对比分析,其中绿色代表原子处于面心立方对称性中,灰色代表原子所处位置不具有晶体对称性。图2所示为结构1沿Z轴方向上每个晶粒包含的原子个数的分布,以及顶部和底部附近的各一个晶粒的具体形貌。其中顶部的晶粒包含60 125个原子,底部的晶粒包含11 432个原子,两者数量约相差5倍。对结构1中Z轴方向晶粒包含原子数进行线性拟合,所得直线的斜率为277。同样地对其他3个结构进行线性拟合,斜率分别为6,11和33。所以从拟合直线的斜率来看,本文构建的4种梯度纳米多晶结构的梯度大小顺序是结构1>>结构4>结构3>结构2。值得指出的是,由于梯度结构是否均匀分布等结构特征并不能从线性拟合反映出来,因而拟合Z轴方向晶粒包含原子数所得直线的斜率并不能完全反应出梯度结构的晶粒分布规律,但仍不失为一种可行的、用于比较梯度大小的方法。

图1 梯度纳米多晶铝示意图Fig.1 Schematic diagram of gradient nano-polycrystalline aluminum
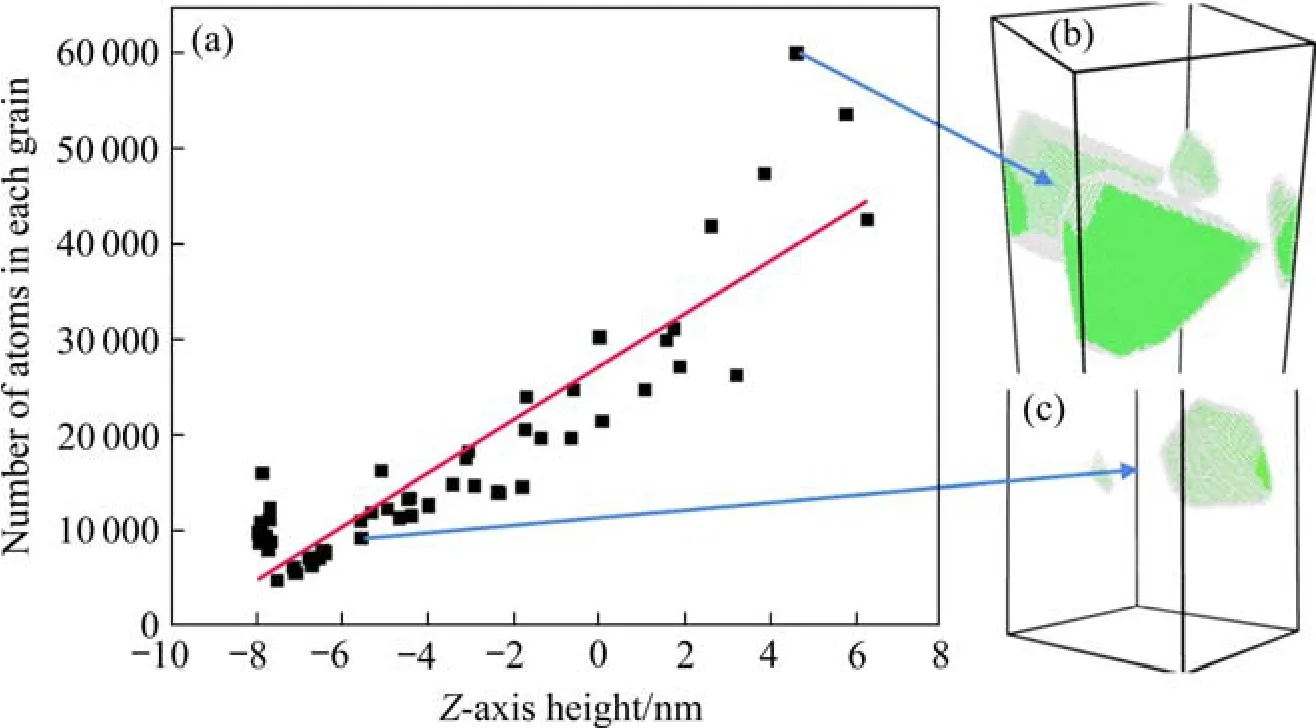
图2 结构1中沿Z轴方向上晶粒包含的原子数变化(a)、顶部附近的大晶粒(b)和底部附近的小晶粒(c)Fig.2 Variation in the number of atoms contained in the grains along the Z-axis direction (a),large grains near the top (b) and small grains near the bottom (c) in structure 1
采用 LAMMPS 软件对梯度纳米多晶铝结构进行分子动力学模拟[20],Al原子间相互作用采用改进型嵌入原子势函数(modified embedded atom method,MEAM)进行描述,与以前的实验结果[21]和DFT计算结果进行比较[22],MEAM势可以很好地计算出Al的特性,特别是缺陷性质,如表面能、点缺陷形成能等。分子动力学模拟中,在变形方向上设置周期性边界条件,其余二维方向则取非周期性,时间步长取为0.000 1 ps。先使用共轭梯度算法对4种不同结构进行能量最小化处理以优化其结构与原子位置,然后在等温等压系综(constant-pressure, constant-temperature,NPT)下将体系温度初始化为300 K,最后在NPT系综下使用velocity命令设置Y轴应变速率发生自-0.1到0.1 nm/ps线性变化,共进行200 000 步的剪切变形模拟,每运行1 000 步输出一次原子所处的位置、应变量与相应的应力、能量与温度等相关性能数据,弛豫及剪切变形模拟时间分别为2和20 ps,使用可视化软件 OVITO[23]中的位错提取算法(dislocation extraction algorithm, DXA)[24]和公共近邻分析方法[19]对模拟体系的位错等微观结构进行分析处理。
2 结果与讨论
2.1 剪切强度
通过对不同结构的梯度纳米结构多晶铝进行剪切模拟,得到不同结构的应力-应变曲线,如图3所示。从图看出,4种梯度纳米结构多晶铝在剪切过程中呈现出较相似的应力变化趋势,即随模拟步数增加,剪切应力先增加到最大值,而后缓慢下降,4种结构的最大剪切强度分别为1.791、1.476、1.414及1.743 GPa,其中具有最大结构梯度的结构 1对应的剪切强度最大。在剪切模拟结束时,不同结构的应变量各不相同,结构1的应变量最小,仅为0.06,而其他3种结构在剪切模拟结束时的应变量分别为0.09,0.10与0.08。
根据从宏观尺度进行的晶体塑性有限元模拟结果[25]可知,在剪切变形过程中,塑性变形首先发生在梯度结构的粗晶部分,但随应变量不断增加,细晶部分开始协调变形。这样可抑制在形变过程中由于晶粒变形程度不一而形成残余应力,进而抑制微裂纹萌生。细晶结构能在一定程度上对材料起到强化作用,结构梯度越高,细晶的晶粒尺寸越小,强化作用也越明显,图3所示的原子尺度模拟结果也显示具有最大结构梯度的结构1的剪切强度最大。原子尺度模拟的优势是可以从原子运动轨迹来分析加载下的微观形变机制,接下来结合可视化软件 OVITO[23]进行剪切过程中微观形变机制的分析。

图3 不同梯度纳米结构多晶铝的模拟剪切应力-应变曲线Fig.3 Simulated shear stress-strain curves of polycrystalline aluminum with different gradient nanostructures
2.2 剪切过程的微观形变机制
使用OVITO软件[23]中的位错提取算法对结构 1、2、3与4在剪切过程中的微观形貌进行分析,不同颜色代表不同类型的位错。从图3可知结构1的剪切强度最大,接下来通过位错及晶粒结构来分析结构1的剪切变形微观形变机制。图4所示为结构1在剪切形变过程中位错的变化情况,图5为剪切过程中结构1的晶粒结构图,图5中橙色圈标记的是层错结构,图4及图5中,从左至右,应变依次为0、0.01、0.03、0.04和0.06(分别对应图3中结构1应力变化曲线上的A、B、C、D、E点,图4为主视图和俯视图,图5为主视图),对应的剪切应力分别为0、1.100、1.791、1.645及1.308 GPa。从图4中可以看出,在剪切变形开始时(图4(a),对应图3中的A点),体系内部位错密度较大,主要是全位错及结构弛豫阶段经全位错分解而得的肖克利不全位错等。大量位错储存在晶界处,少部分在晶粒内部,分布呈现明显的不均匀性,即粗晶区域的位错密度高于细晶区域。粗晶区域晶粒尺寸较大,故晶内可容纳的位错较多,而细晶区域晶粒细小且晶界面积较大,因此晶粒内部的位错数量较少,同时大部分位错易塞积在晶界处。随着剪切形变的发生,在剪切应力增长至1.100 GPa的过程中(图4(b),对应图3中A到B点阶段),剪切强度逐渐增加,晶粒内部位错逐渐向晶界方向移动并在此塞积,大量全位错向肖克利不全位错转化,此后随剪切应力值增长至最大值1.791 GPa时(图4(b)和(c),对应图3中B到C点),剪切强度进一步升高,有更多位错在晶界塞积,且由于在变形过程中部分已塞积位错获取更多能量得以穿越晶界并最终在表面释放。在位错释放的同时,晶粒内部开始出现贯穿整个晶粒的层错结构(图5(c)中橙色圈标记部位)。这些贯穿整个晶粒的结构可以起到阻碍与之相交的滑移系统滑移的作用。此后,剪切变形将集中在此区域发生。在这一阶段,结构内位错塞积作用大于位错释放作用。当体系达到最大剪切强度时(图4(c),对应图3中的C点),在晶界区域出现明显的位错塞积现象,大部分晶粒形态没有发生明显的变化,晶粒内部位错密度较小,而在晶粒取向异于剪切方向的晶粒,其晶界处位错密度很大,没有产生明显的层错,此时,结构内的位错塞积作用与位错释放作用达到平衡状态,因而剪切强度取得最大值。在剪切应力降低到1.645 GPa的过程中(图4(c)到(d),对应图3中的C到D点阶段),随着剪切形变持续进行,晶粒内的大量位错逐渐穿过晶界并在表面释放,此时,晶粒内部位错密度明显降低,剪切强度也逐渐减小,在晶粒取向与剪切方向不同的晶粒内部有一定数量的层错(图5(d)中橙色圈标记部位)生成,这些层错也逐渐向晶界方向移动,在这一阶段主要存在位错的释放作用。在剪切过程结束时(图4(e),即图3中的E点),结构1的内部位错数量比其他状态下的低,剪切应力也降至1.308 GPa。
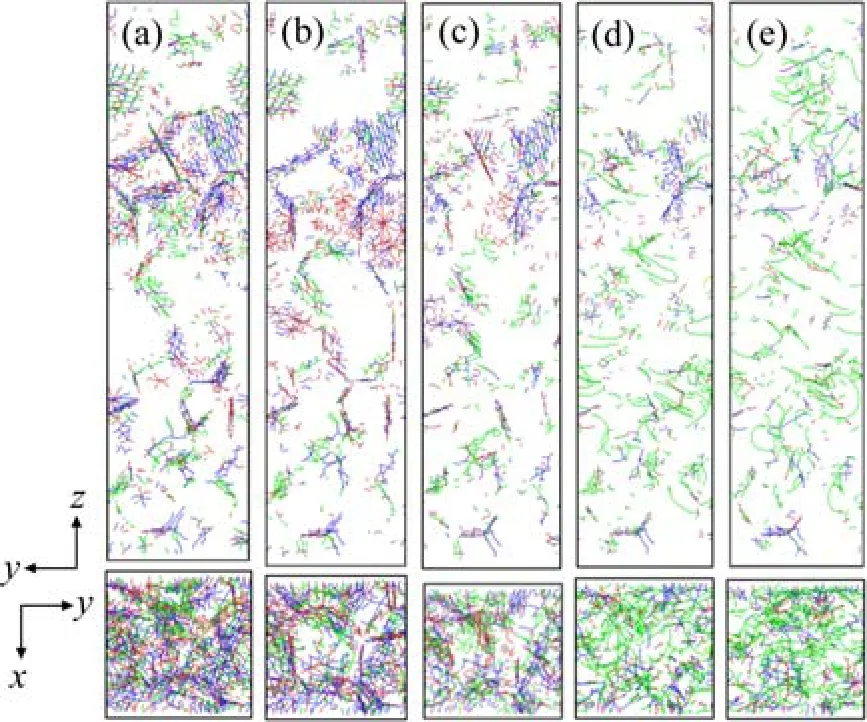
图4 结构1在剪切形变过程中的位错演化Fig.4 Dislocation evolution of structure 1 during shear deformation

图5 结构1在剪切形变过程中的晶粒结构图Fig.5 Grain structure diagram of structure 1 during shear deformation
为进一步探究剪切形变过程中体系微观结构的变化,图6给出了结构1剪切形变前后的晶粒形变情况,图中深绿色块状部分表示用公共近邻分析方法算出的处于面心立方结构的晶粒,而红色、蓝色等线条是用位错提取算法得到的位错线,其中灰色代表的所处位置不具有晶体对称性的原子被去掉,以便于清晰地看出各个晶粒在形变前后的变化情况。从图6可以看到,在剪切形变终止时,结构1内少部分晶粒内部均形成了明显的层错结构(图6(b)中橙色圈所标记的部位),但并无贯穿整个结构的剪切带出现。观察图6还发现在剪切形变结束后,模拟体系内部的部分粗晶粒分解为几个小晶粒(图6(b)中蓝色圈所标记的部位),而其余晶粒则无明显可见变化,推测可能与晶粒取向差异和晶粒旋转等原因有关。

图6 结构1的晶粒结构图Fig.6 Grain structure diagram of structure 1
图7所示为结构3在不同应变时的晶体结构示意图,从上至下应变依次为0、0.015、0.040与0.100,图8为其对应的位错分布图。不同颜色表示内容与图6一样。图7中用红圈标记出一个较大晶粒,蓝色的连续线条表示在模拟体系中形成的剪切带。结合图7与图8可以看出,由于晶粒取向(沿短轴方向)与剪切方向间存在较大差异,随着剪切形变的逐渐进行,标记晶粒出现了明显变化。首先在应变逐渐增长到0.015,即图7(a)到图7(b)与图8(a)到图8(b)阶段,晶粒内部的位错向晶界方向的运动,有部分塞积在晶界处,但没有跨越晶界(如图8(a)与(b)中红色圈记部位所示)。在应变逐渐增长至0.04的过程中,即图7(b)到(c)与图8(b)到(c)阶段,出现大量位错,进一步加剧塞积,且一些塞积位错跨越了晶界,出现应力释放(如图8(c)中红色圈记部位所示)。在最大剪切强度对应的图7(c)与图8(c)中,晶粒内部出现许多层错结构,其边缘对应相应的位错线。这些层错结构是后续形变过程中晶粒发生破碎的基础。在剪切变形过程持续进行的同时,晶粒内大量位错逐渐穿过晶界并在表面释放(如图8(c)中红色圈记部位所示),此时,晶粒内部位错密度明显降低,剪切强度也逐渐减小。在晶粒取向与剪切方向不同的晶粒内部有一定数量的层错生成,这些层错也逐渐向晶界方向移动并最终在已经形成的剪切带区域释放,使得剪切带进一步生长。当应变进一步增长至0.10,即图7(d)与图8(d)所示的剪切终了态时,晶粒取向与剪切方向不同的晶粒内部有大量层错释放,有贯穿整个多晶结构的剪切带形成。非剪切带的区域位错密度较低,主要是因为在剪切带形成过程中该区域有大量位错释放,同时已生成的剪切带对与之方向不同的滑移体系的激活有抑制作用。由于晶界迁移与晶粒旋转的共同作用,使取向与剪切方向不同的部分晶粒逐渐破碎并最终消失,在晶界处则有大量被释放的塞积位错聚集形成剪切带。可以看出,该剪切带是在剪切变形过程中,由初始状态下相邻且具有相近取向的晶界经由运动位错在此处的塞积及释放而形成的,该剪切带的形成是导致结构3在剪切模拟中的剪切强度最低的原因。
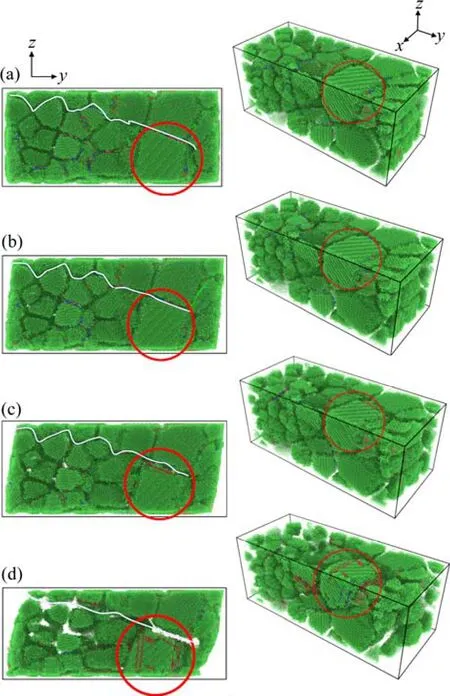
图7 剪切形变过程中结构3的晶粒结构变化Fig.7 Grain structure of structure 3 during shear deformation Strain: (a) 0; (b) 0.015; (c) 0.040 and (d) 0.100
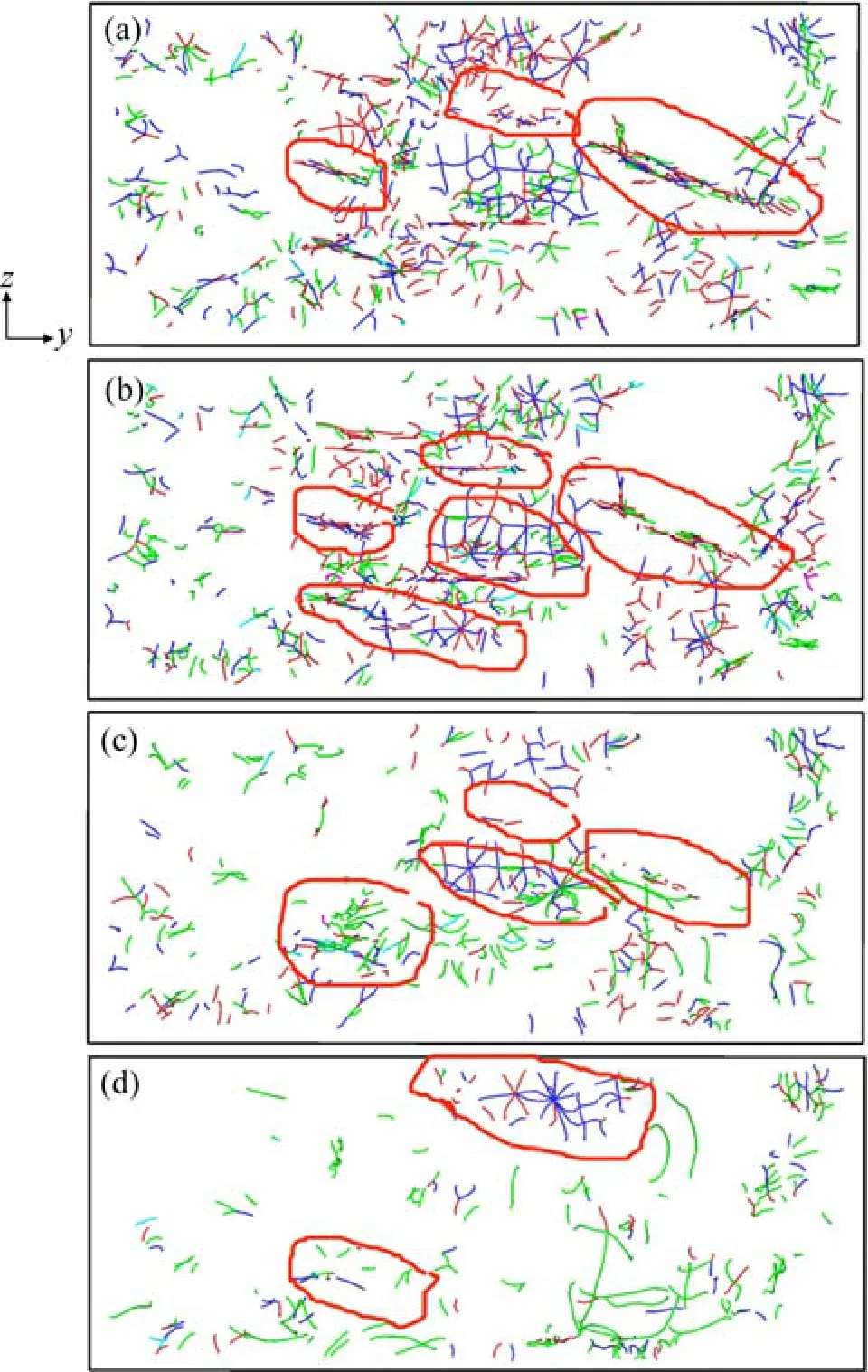
图8 剪切形变过程中结构3的位错演化Fig.8 Dislocation evolution of structure 3 during shear deformation
3 结论
1) 结构梯度最大的结构1具有最大的剪切强度,梯度纳米多晶铝内部初始的位错密度较大,随着剪切形变的进行会发生位错在晶界塞积,位错穿越晶界与位错逐渐释放的过程。
2) 由于梯度纳米结构的存在,部分粗晶会由于晶粒取向与剪切方向差异较大和晶粒旋转等原因分解为几个较小的晶粒,而细晶粒则无明显变化。
3) 在变形过程中由于位错塞积与释放及晶界的相互连接而形成的剪切带会严重影响梯度纳米结构剪切强度的大小。

