基于粘弹塑性模型的二维土体非线性地震反应分析

杨笑梅，陈鑫，游昊冉

（广东工业大学土木与交通工程学院，广东 广州 510006）

引言

包含沉积土层的复杂场地地震反应及地表放大特征分析对防灾减灾及结构的抗震设计至关重要［1］。由于现有强震观测台站还不足以覆盖所有城镇区域，且强震观测数据还远不够预测工程中需要的地表反应特征［2］，因此，地震波在复杂沉积土层传播特征的研究仍主要依赖波传播理论及数值模拟的手段［3］。目前通用有限元软件在复杂场地数值模型建立上存在很大优势［4］，但在覆盖土层的非线性与吸能特征［5］及人工边界设置上还很难达到要求。特别是对土体非线性特征的模拟，通用软件内置的常规非线性本构模型如摩尔库伦模型（Mohr-Coulomb）、D－P模型（Drucker-Prager）、剑桥模型等［6］并不适用。主要是因为这类模型均采用与动力分析不同的硬化规律，不能体现动力作用下应力路径特征［7－8］。另外，工程中使用最广泛的土动力本构模型是Idriss［9］提出的等效线性化模型。该模型虽然可以在一定程度上模拟土体的非线性及吸能特征，但其在软土及强非线性反应中的模拟合理性一直受到质疑。因此寻求简单有效的非线性本构模型，借助通用软件使其适用于模拟土体高维非线性地震反应一直是复杂场地地震反应分析中重要的研究内容。

目前粘弹塑性本构仍是公认的能反映土体真实非线性特征的理论模型，其更适用于强震下的地震反应分析。Iwan［10］模型作为经典的土体动力非线性分析模型的代表，一直广泛应用于土动力反应分析问题。很多学者在Iwan串联模型基础上进行改进，使其更适用于相关的研究问题。如为了合理考虑软黏土的应变软化特征，Rao等［11］借鉴Idriss等［12］软化模型，进一步修正了Iwan串联动力本构模型。在众多描述土体非线性的粘弹塑性动力本构模型中，通常存在理论复杂，推导过程参数众多等问题，且通过土动力学试验确定的土体参数离散性较大，计算结果的可靠性常存在争议。因此，很多模型还仅限于理论研究层面，难于应用到实际工程分析中。Joyner和Chen等［13－14］于1972年将Iwan串联模型应用于高维非线性地震反应研究中，由于采用了合理硬化规律，不仅在模拟应变硬化土体时得到较好的结果，而且在应变较小时模拟应变软化类土体也能达到较高的精度。特别是该模型相对于众多的同类土体动力非线性模型来说，具有同等效线性化相类似的参数选取功能，较其他类似弹塑性本构模型具有参数简单，易选取，模型稳定性较好等特征。

为了能借助通用软件的强大数值模拟功能，并使其适合模拟包含土层的高维地震反应，文中从二维波动问题出发，基于ABAQUS的显式计算过程：（1）推导了与其显式计算相匹配的粘性边界，解决了ABAQUS软件无法直接模拟二维无限域波动问题的困难；（2）在Joyner［13］基于Iwan串联模型发展的土体动力本构模型基础上，考虑了土体的吸能特征，引入瑞利阻尼模型进行改进，使其适用于模拟土体的粘弹塑性分析；（3）借助通用软件ABAQUS的良好开放性［15］，利用其中二次开发功能子程序VUMAT，将本构模型植入其中，克服ABAQUS自带本构模型难以较好地模拟土体地震反应的劣势。为了验证文中方法，选取2个二维典型算例，进行地震反应分析并与参考解对比，吻合度较好。进一步选取文献［16］的典型盆地为研究对象，通过与文献［16］计算结果对比，探讨了文中本构模型的参数选取原则，并阐述参数选取的灵活性及简便性，为其能进一步应用于复杂工程场地地震反应分析提供指导。

1 2D P－SV波传播模拟在ABAQUS中的实现

2D场地地震反应问题理论上属于无限域二维P－SV波传播问题，通用的有限元软件无法直接模拟。需要解决人工边界设置、土体的非线性本构模型及土体的阻尼模型建立等相关问题。为了更好地阐述文中构建的计算过程，本节将简要介绍其相关理论及其在ABAQUS中的实现。

1.1 粘性人工边界条件及地震输入在ABAQUS中的实现

为了实现地震波在无限域传播的合理模拟，需要在建立的有限域分析模型边界设置特殊的边界条件，以保证地震波传播过程中不会在边界处产生伪波。本计算过程采用由Lysmer等［17］提出的粘性人工边界模型，通过在ABAQUS建立的有限元模型边界处合理设置阻尼器实现。具体的阻尼器参数计算公式如式（1）：

式中：下标N代表法线方向；下标T代表切线方向；ρ为密度；vp为纵波波速；vs为剪切波波速；A为单元面积。

地震输入以等效结点力F实现［18－19］，计算公式如式（2）：

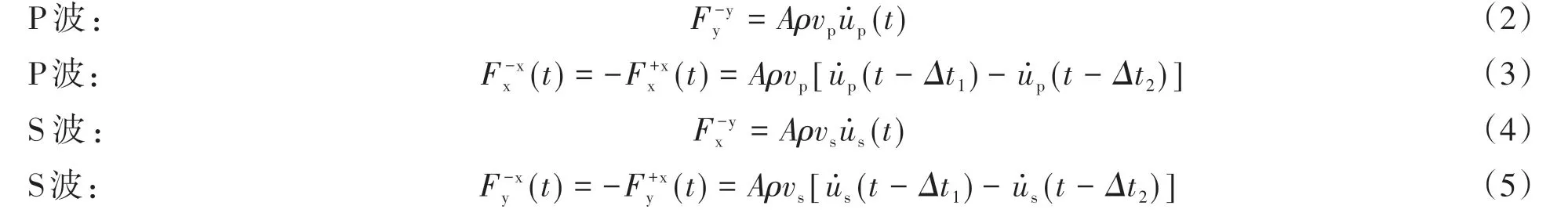
式中：下标x或y表示施加于结点处力的方向；上标x或y表示外法线方向；Δt1及Δt2分别表示边界处入射波和反射波的延迟时间。

1.2 多屈服面本构模型理论简介

文中建立的本构模型是基于Joyner［13］在Iwan［10］模型基础上改进的二维多屈面模型，由于该模型对应力路径能够合理记忆，因此在任意复杂的往复荷载作用下模拟其加卸载曲线均能达到较好的结果。为理解文中计算过程，先简要介绍文献［13］中的多屈面本构模型。

1.2.1 相关应力应变量的定义

文献［13］所用的弹塑性模型将采用平均应力σM，平均应变eM，偏应力σij和偏应变eij的概念，定义分别如下：

式中：Sij和Eij分别表示总应力及总应变；δij为Kronecher符号。由式（6）及式（7）可知，总应力或总应变量是通过计算出平均应力或应变及偏应力或应变后求得。模型假设塑性应变全都是由偏应力产生，平均应力及平均应变关系为线弹性。

1.2.2 多屈面模型的假设

文中弹塑性模型假设主要采用文献［13］的理论确定偏应力应变增量关系，该模型的屈服准则、加卸载准则、移动硬化定律以及流动法则描述如下：

（1）屈服准则

土体在偏应力空间的应力状态下，假设有一系列的屈服面，满足如下屈服函数：

式中：F是屈服函数；αij表示移动硬化参数；k表示与屈服强度相关的常数；下标n代表第n个屈服面。

（2）移动硬化准则

为了体现动力作用，Joyner采用式（10）作为移动硬化定律，从而保证应力点和屈服面的一致性：

式中：上标含“p”的物理量表示前一时刻的计算值，上标含“p+1”的物理量表示当前时间步的计算值。

（3）流动法则

文中采用如下的流动法则描述塑性变形增量的大小和方向：

这里新出现的变量Ln与加卸载准则相关，具体参数如下节，而hn为非负的塑性标量因子，由式（12）计算：

式中，cn为第n个屈服面的屈服面系数。

（4）加卸载准则

土体受到往复动力荷载作用时，假设的加卸载准则如下：

1.3 土体阻尼模型的选取

土体除了具有非线性特征还存在较强的吸能特征。选取在计算过程中保持定阻尼值的瑞利阻尼［20］考虑土体的耗能特征。参考文献［21］给定的计算公式确定阻尼系数，即：

式中：α、β为瑞利阻尼系数；ξ为土体阻尼比系数；f1和f3分别为线性场地1，3阶频率。

1.4 弹塑性模型VUMAT子程序的实现流程

利用了ABAQUS二次开发编写了对应文中弹塑性本构计算的VUMAT子程序，具体计算过程描述如下：（1）读入由ABAQUS数据文件给定的初始总应力、总应变、初始状态变量值，并根据式（6）及式（7）计算平均应力及偏应力，平均应变及偏应变初值；（2）调用VUMAT子程序，由ABAQUS中读取的位移值，计算平均应变增量及偏应变增量；（3）由平均应变增量计算平均应力增量；（4）按弹性本构模型计算试探应力，并根据计算结果按屈服准则即式（8）及式（9）判别是否屈服，若判别结果为弹性，则子程序自动更新应力及应变值进行下一个增量步的计算；（5）若判别为塑性，按塑性理论要求计算，遵循文中的移动硬化准则、流动法则及加卸载准则由偏应变增量计算偏应力增量；（6）由计算所得的平均应力增量及偏应力增量，更新偏应力及总应力，并由平均应变增量及偏应变增量更新偏应变及总应变值；（7）重复（2）～（4）步直至计算停止。

2 基于ABAQUS数值模拟过程P－SV波传播问题的验证

为了验证文中计算过程的正确性，本节通过2个算例分别验证二维波传播问题边界设置的合理性及多屈面本构模型的可靠性。

2.1 半圆峡谷地形地表反应

为了验证文中方法与计算的正确性，选取Kawase在文献［22］中基于离散波速边界元法分析的无限域半圆峡谷地表反应问题进行分析，为了便于结果的比较，类似文献［22］，计算时定义一个与频率相关的参数：

式中：λS为弹性介质中剪切波波长；νS表示弹性介质剪切波波速；a表示半圆半径。文中η取2，介质计算参数如下：νs=200 m/s，密度ρ=1 800 kg/m3，泊松比υ=1/3；半圆峡谷模型计算参数取为：L×h=800 m×200 m，峡谷半圆半径a=50 m。基于有限元软件ABAQUS建立二维SV垂直入射线弹性有限元模型，如图1（a）所示，边界处网格尺寸为1 m×1 m。在边界处设置阻尼器模拟外部无限域，如图1（b）所示。根据式（1）计算边界处相应阻尼器参数，并将地震输入等效为结点力添加在边界，边界力值利用式（2）～式（5）计算，进行时域显式分析，为了对比，地表水平与垂直方向的各点位移响应结果转化为频域结果，如图2所示，图2同时给出了Kawase计算结果。

图1 半圆谷地有限元模型及局部粘性边界Fig.1 The finite element（FE）model for semi-circular canyon and its local viscous boundary

从图2结果对比可见。本文解与文献［22］计算结果比较吻合，边界反射的误差波未对结果产生影响，也说明地震波可以由边界处外传出计算域，x表示该点到谷地中央的距离，x/a为无量纲物理量。因此文中基于ABAQUS二维显式有限元结合设置人工边界及地震输入的计算过程可以合理模拟二维无限域线性地震反应。

图2 半圆谷地地表位移幅值（η=2.0）Fig.2 The displacement amplitudes on surface of semi-circular valley for η=2.0

2.2 二维土体非线性算例

为了校验本构模型，选取Willam B.Joyner文献［13］的土坝模型算例进行模拟，计算模型如图3所示，依据原文网格尺寸取为9 m×9 m，土坝土层主要由黏土与颗粒状物质组成，土体动力参数请见表1，因文中本构模型参数主要包括抗剪强度、剪切波速、动剪切模量、屈服面数及阻尼参数，而文献［13］未考虑阻尼故此例忽略该参数。地震动输入为N21E方向的TAFT波，为了模拟强震输入下土体的非线性特征，按原文的方法，将输入地震波整体乘以4倍调整速度峰值为0.7 m/s，输入地震动时程见图4。参考原算例，在土坝的表面设置了5个输出点（如图3中1－5所示），模拟结果为速度时程，结果如图5所示。为了比较，文献［13］中对应5点的速度时程结果也绘于图5。图5显示文中结果与文献［13］结果吻合较好，验证了文中本构模型的正确性。

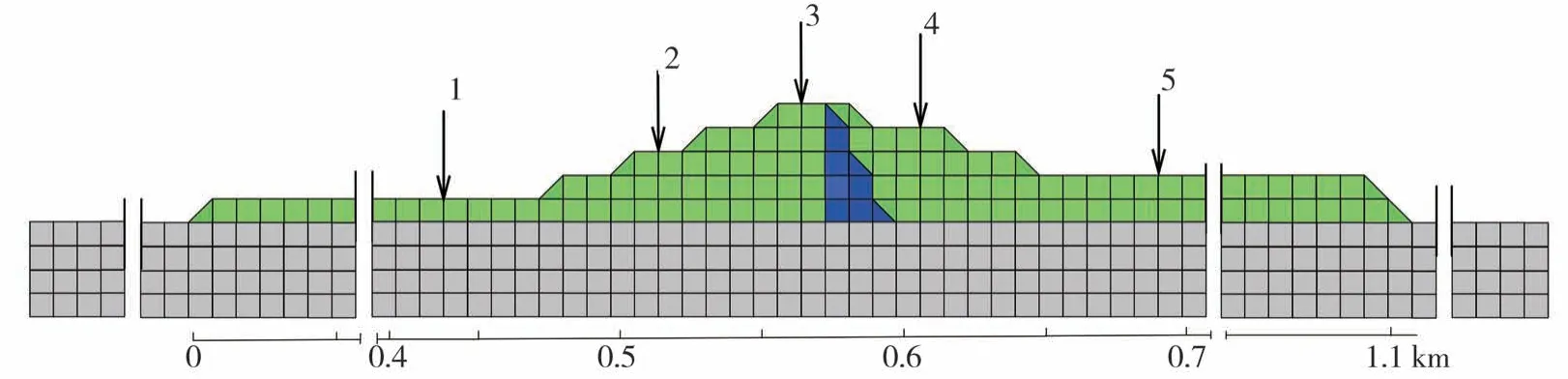
图3 土坝简化FEM模型［13］Fig.3 Simplified FEM model for earth dam［13］

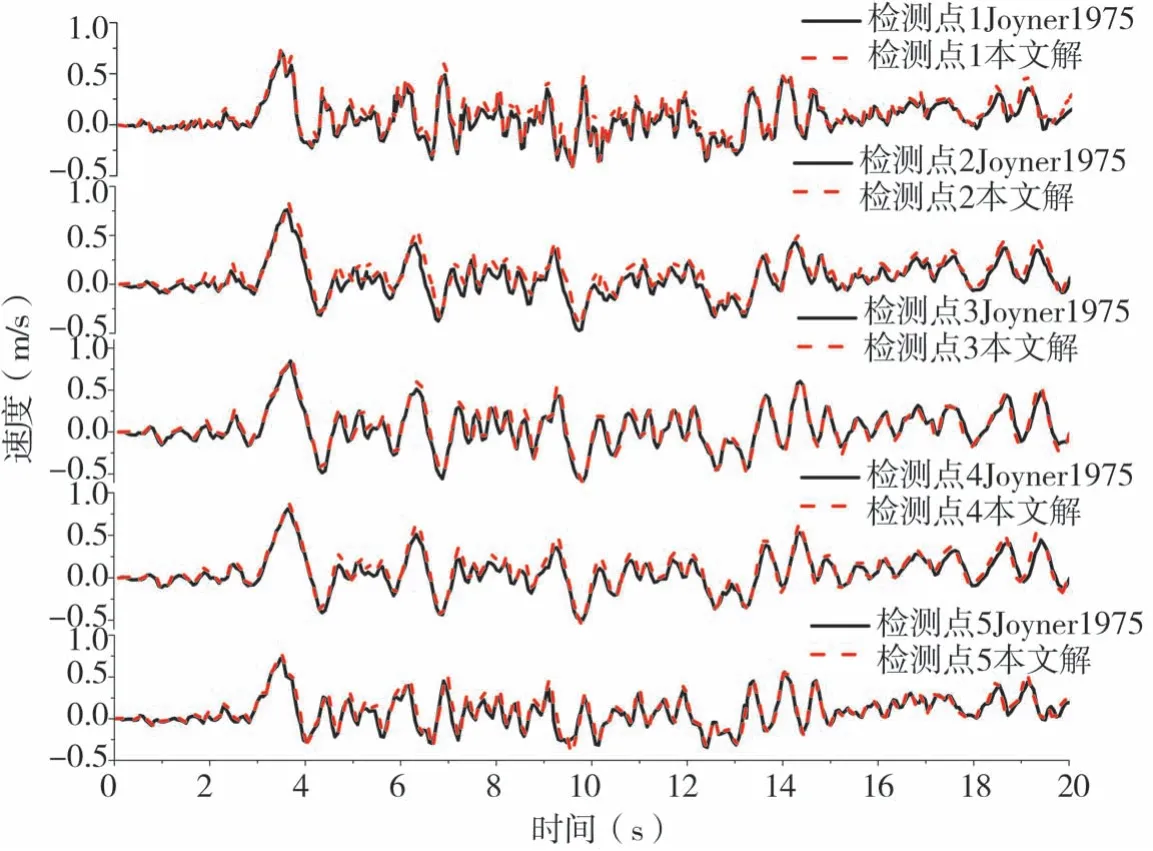
图5 地表指定点（图3所示）的水平速度时程Fig.5 The horizontal velocity time histories at the points on surface prescribed in Fig.3

表1 土体参数［13］Table 1 Soil parameters［13］

图4 基底输入地震动时程［13］Fig.4 Time history of base-input ground motion［13］

3 非线性反应分析参数设置问题的讨论

弹塑性本构模型模拟土体非线性反应时，除上节给出的参数外，还需要设置很多与非线性分析相关的参数，参数选取时通常会遇到困难，导致很多本构模型很难运用于实际问题分析。相对多数弹塑性模型，文中本构模型参数相对简单稳定，更适用复杂地质条件特别是含有复杂土介质的地震反应分析。本模型依赖的非线性分析参数主要包含抗剪强度、剪切波速、动剪切模量、屈服面参数以及粘性阻尼参数等，可以很容易通过实验直接获取或通过等效线性化模型的模量比曲线参数转化，不需要增加额外的工作。为了更好地理解本模型参数选取的规则，文中以文献［16］中的欧洲高山盆地简化的非对称场地模型为研究对象，采用文中方法模拟盆地地表反应进而阐述非线性相关参数选取的原则。如图6所示，选取的计算模型尺寸总长约1 000 m，高约250 m，土层最大宽度约500 m，沉积土层最深处约225 m，共7层，场地左侧边界平直，右侧边界简化为圆弧。输入地震动为Ricker子波，见图7。文献［16］中土层统一了密度，具体土体物理参数见表2，土体动三轴试验结果参见图8。依据现有这些常规数据，下面将简介本算例模拟过程中需要但未给定的相关参数选取原则。

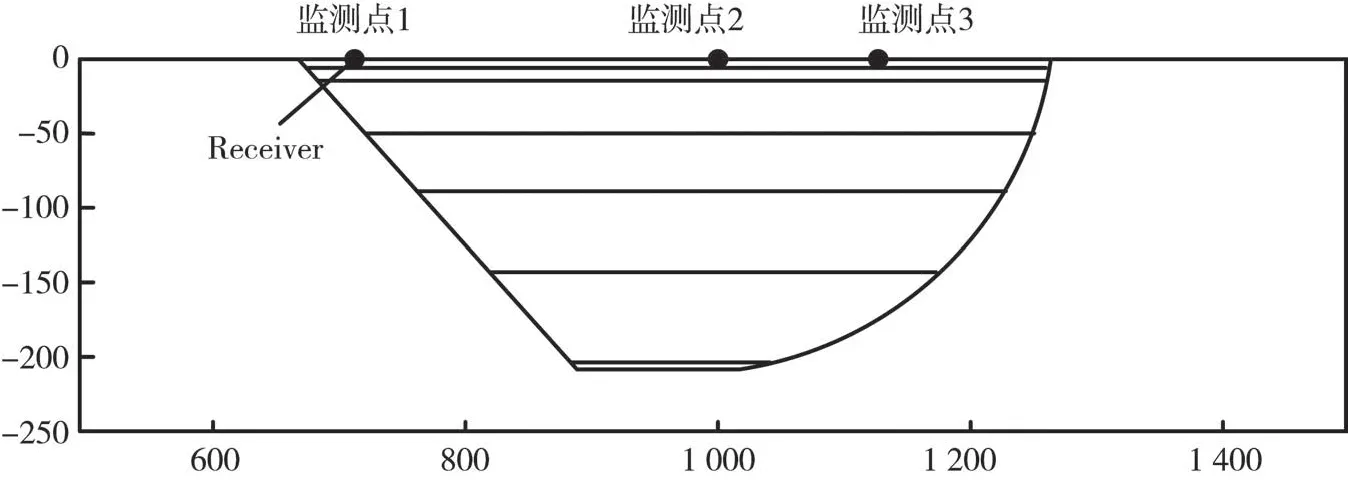
图6 盆地模型图［16］（单位：m）Fig.6 Basin model diagram［16］（Unit：m）

图7 地震输入Ricker波时程［16］Fig.7 Time histories of seismic input of Ricker wave［16］

表2 土体的物理参数［16］Table 2 Physical parameters of the soil layers［16］

3.1 动剪切模量的确定

在非线性问题中剪切模量是随着加载强度而变化的物理量。确定动剪切模量一般有2种方法：一是通过实验直接得到，如文献［13］的做法；另一种通过现场测量剪切波速及动三轴给出的刚度曲线参数换算得来［23］。因文中选取的盆地分析模型已提供了土体的物理参数及模量比曲线，故文中采用换算的方法计算动剪切模量。根据文献［23］，土体在低应变情况下的最大剪切模量Gmax由式（15）计算：

式中：νs为土体的剪切波速；ρ为土体密度。根据文［16］给出的盆地土层剪切模量比曲线（图8），当前应变状态下的动剪切模量G的计算公式为：

式中：γ为剪应变；f(γ)为不同剪应变下G/Gmax的比值。

3.2 抗剪强度的选取原则

抗剪强度也是模拟土体非线性特征的重要参数之一，其值与动剪切模量直接相关。由上节公式，抗剪强度τ可通过换算得到，计算公式如下：

根据式（17）将图8的剪切模量比曲线转化为图9的应力应变曲线，再通过图9的应力应变曲线可以直接获得本模型每层土体的最大抗剪强度。

图8 模量比曲线Fig.8 Modulus ratio curve

图9 应力应变曲线Fig.9 Stress-stain curv

3.3 屈服面系数及屈服面数量的选取

文中采用的非线性本构模型属于弹塑性多屈面模型，因此计算中需要给出与屈服面相关的分析参数，主要包括屈服面系数和屈服面数量，其中屈服面系数为常数，可以通过室内实验直接获取，也可通过递推公式计算［13］给出：

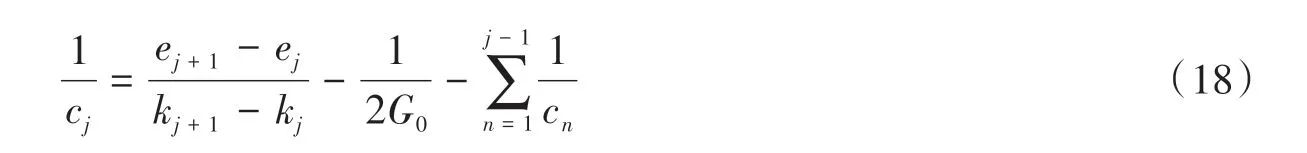
式中：cj表示当前待计算的屈服面系数；cn表示以往已计算的屈服面系数；e表示该屈服面上剪应变值的归一值；k表示该屈服面上切应力值的归一值，下标j及j+1分别表示当前及下一个屈服面。

因土体具有较强非线性特征，即在较弱荷载作用下土体仍会进入塑性，故其弹性域几乎可以忽略不计，但文中本构模型仍然保留了较小的弹性域，通过增加屈服面数量达到减小弹性域的目的。文中假设仅取第一个屈服面的范围为弹性域，随着屈服面数量的增多、第一个屈服面的范围越来越小，弹性区间也相应变小，塑性区间相应增大。为了讨论屈服面数量合理取值范围，文中通过将屈服面数量（以下用n表示）分别取为10、20、50、100，以Ricker子波为基底地震输入（图7），输入加速度时程的峰值（PGA）分别取为0.5、2.5、5 m/s2进行模拟，分别计算地表3个监测点（图6）处的加速度时程反应及其傅氏谱，以n=100计算结果为标准，由式（19）计算地表1～3监测点曲线的均方根误差，计算所得的地表时程、傅氏谱误差分别见图10和图11。

图10 地表加速度时程误差Fig.10 Errors of acceleration time histories at the points prescribed

图11 地表傅氏谱误差Fig.11 Errors of Fourier spectra at the points prescribed

式中：RMES为所求均方根误差；n代表屈服面数；m代表加速度时程或傅氏谱的数据点数。

从图10及图11的对比结果来看，屈服面数量的差异对地表地震反应的模拟结果具有一定的影响。总体来说屈服面数量越多，计算精度越好。从图10及图11反映的误差分析结果可以看出n=50时计算结果良好，而n=10时模拟结果与n=100的结果还是有着有意义的差异，n=20相对于n=10的结果与n=100的时程结果吻合度尚可。从两图中可以看出3种强度下均体现类似的规律，即n=50误差非常小，可以忽略。n=20的误差也是可以接受的，而n=10时无论模拟的时程还是傅氏谱，均存在较大的差异，不建议选用。通过以上分析可以看出，屈服面数量选取应大于20。考虑到计算效率与计算精度的匹配及数值模拟结果，建议屈服面数量取为20，此时屈服面数量对地震反应分析的差异影响变小。

3.4 数值对比分析

GÉLIS在文献［16］中采用相似的弹塑性本构模型模拟了图6描述的盆地，基于GÉLIS在文献［16］中给出的参数及计算模型（图6），采用文中方法对该场地模型进行模拟。通过与GÉLIS的模拟结果进行对比，验证文中分析过程的可靠性。

根据3.1及3.2节的说明，计算本模型的动剪切模量，抗剪强度。根据3.3节的讨论，本计算过程屈服面数量取为20，屈服面系数由式（18）计算，阻尼系数由式（13）计算。图12及图13分别给出了地表3个监测点的速度时程及其反应谱的模拟结果，为了对比，图中还给出了文献［16］的对应解。

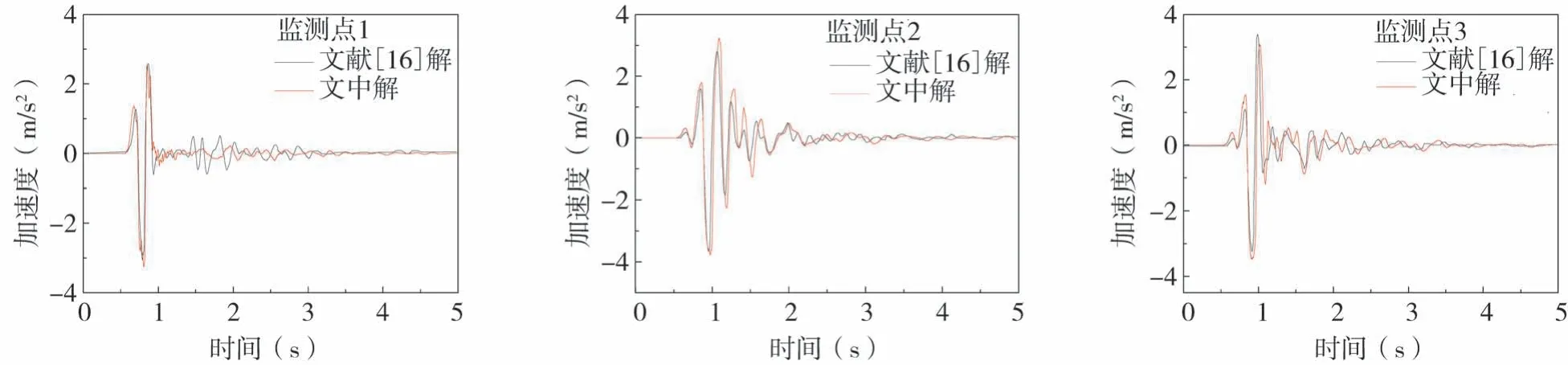
图12 监测点（图6所示）加速度时程Fig.12 Acceleration time histories of the output points prescribed in Fig.6

从图12中的结果可以看出文中给出的3个输出点的时程反应与文献［16］的结果基本吻合，无论是时程曲线波形还是峰值均比较接近参考解，只是在监测点1处的时程在1.5～2 s之间与参考解稍微不同，这个特征主要在于对盆地产生的面波反应分析存在稍许差异，可能是阻尼参数选取差异的影响。图13计算的傅氏谱存在稍许差异，监测点2及监测点3的特征周期值与参考解基本吻合，特征周期处的傅氏谱峰值稍有差异，这可能也源于文中采用了与文献［16］不同的阻尼模型假设。对监测点1，文中解与参考解存在一定的差异，主要体现在傅氏谱峰值对应的特征周期相对于文献［16］解略小。原因可能是分析模型介质参数存在一定差异或输出位置不同而产生的影响。通过对时程反应和傅氏谱模拟结果总体分析，文中解与文献参考解的计算规律基本吻合，说明文中计算过程及分析参数选取方法是基本合理的，应用文中计算过程分析二维复杂土层地震反应是可靠的。

图13 监测点（图6所示）加速度时程傅氏谱Fig.13 Fourier spectra of accelerations on the points prescribed in Fig.6

4 结论

文中在通用软件ABAQUS的基础上，建立了适用于包含复杂土层场地的二维地震反应分析过程，使其可以同时考虑土体结构空间的复杂性及土体的非线性及粘性特征。通过对本分析过程的论证，可以得出以下一些结论：

（1）文中设置的粘性边界，可以使外传波成功通过人工边界，保证计算的合理性。

（2）文中选用的非线性动力本构模型适用于土体二维地震反应分析，能合理模拟土体的非线性特征。

（3）相较于现有二维动力本构模型，文中选取的动力非线性本构模型具有参数简单，易选取的特征，可以利用等效线性化模型参数直接转化，也可以通过土样试验直接获得。

（4）文中计算过程是基于ABAQUS的显式计算过程，具有良好的计算效率，并可以实现较大的计算规模，为大尺度非线性地震反应分析过程的实现提供了借鉴。