生态框架结构加固浅覆盖层边坡的地震动力响应
牛家永,张建经,张灏蒸,张旭皓,何俊松,江学良
(1.西南交通大学土木工程学院,四川 成都 610031;2.中南林业科技大学土木工程学院,湖南 长沙 410004)
引言
我国西南地区地震频发,尤其是四川省境内活动性断裂带十分发育,历史上发生过多次7级以上强震[1]。山区公路沿线也因此产生了大量地震滑坡灾害,其中浅覆盖层边坡具有分布范围广、隐蔽性高、突发性强等特点,给铁路、公路等交通运输带来了严重的安全隐患[2]。
混凝土框架锚杆结构作为一种边坡主动防护结构,能起到兼顾边坡的深层加固与浅表层护坡,同时由于格构梁柱整体刚度大,使得坡面的受力、变形较为均匀,因此在高烈度地震区的浅覆盖层边坡、软弱夹层边坡和基覆边坡的加固中得到广泛应用。国内外学者对此类结构开展了大量的震害调查[3]、振动台模型试验[4-5]和数值仿真[6-7]工作,认为其在地震作用下具有较好的整体抗震性能。但是,混凝土结构存在变形协调性和可恢复性较差的问题,在地震作用时也存在框架梁被剪断、锚杆框架梁连接处开裂失效、坡面框架梁无约束处岩土体滑塌等局部破坏现象,从而影响到整个支护结构发挥作用。另外混凝土结构还伴有工程造价高、现浇结构施工慢、对生态环境破坏性大等问题。
近年来,国家越来越重视生态环境保护、节能减排和绿色高质量发展,并出台了一系列方针政策。在浅覆盖层边坡加固方面,目前仍大量混凝土结构,其无法与生态环境协调共存,不符合当前的绿色化发展需要,急需研发一种新型的装配式生态护坡结构,以实现在全生命周期内减小对生态环境的影响。西南地区竹类资源丰富,与混凝土、木材、砌体等传统建筑材料相比,竹材具有生长周期短、加工能耗低、废弃后可自然降解等优点,是公认的天然绿色建材[8]。按照制作工艺的不同,工程竹主要可以分为胶合竹材、竹木复合材料、重组竹材等类型。其中,重组竹是一种竹基纤维复合材料,被广泛用作装配式建筑物的承重构件。研究表明[9-10],重组竹与木材相比,具有强重比高、塑性好、能够吸收和耗散大量地震能量等优良性能。经防腐处理后,能够达到I级强耐腐要求[11]。在节点连接方式上主要采用钢夹板或者钢套筒螺栓连接的方式,此种连接方式具有安全可靠、施工快捷、制作简单等优点[12]。因此,借鉴重组竹结构在建筑工程领域多年来成功应用的经验,将其引入到岩土工程边坡防护中,可为生态护坡结构的设计和发展,以及边坡工程创面的修复提供借鉴和参考。
文中设计了一种结构形式为“竹制框架+锚杆”的新型生态耐震型框架结构,并开展了大型振动台模型试验。通过加载不同强度的天然地震波和不同频率的正弦波,分别从时域、频域和时频域3个角度分析了边坡加速度动力响应规律。利用位移响应峰值分析了浅覆盖层顶部和坡面的位移动力响应规律。最后结合试验宏观变形破坏现象,总结分析了边坡在地震作用下的破坏模式。
1 振动台模型试验概况
1.1 防护结构设计
川西峡谷区是西南高山亚高山区的典型地形条件之一,主要分布在成都平原川西高原的过渡地带,以及川西高原与青藏高原的交接地带。高山峡谷地区由于活动断裂带广泛分布,5级以上地震频发,加之创面土质条件较差,道路工程沿线时刻面临着崩塌、滑坡、泥石流等浅层地质灾害的威胁。2017年九寨沟7.0级地震的震害调查[13]表明地震诱发的地质灾害主要以中小型浅层滑坡和崩塌为主(如图1所示),且受人类工程活动影响较大,主要分布在道路两侧0~500 m范围内。针对这种单体规模小,但总体密度大的浅层滑坡类型,进行大规模的混凝土框架防护已不是一种经济有效且低碳环保的治理方法,需要设计一种抗震韧性边坡防护结构[14]。

图1 九寨沟地震诱发的浅层滑坡Fig.1 Shallow landslide induced by Jiuzhaigou earthquake
采用重组竹作为框架梁的横梁和纵梁,钢套筒螺栓连接件作为装配节点,设计了一种新型生态耐震型框架结构,其结构形式为竹制框架与锚杆结构。竹制框架梁主要起到压土作用,避免由于坡面客土的局部破坏而引发坡体大范围失稳,而锚杆能够有效防止覆盖层沿基覆面滑动界。重组竹和钢套筒螺栓连接的节点设计,不仅可以避免传统卯榫连接对梁柱截面的削弱,又能充分发挥钢材良好的弹塑性变形能力,使节点处具有较高的承载力和耗能能力。设计的竹制框架与锚杆结构示意图如图2所示。参考公路路基设计规范(JTG D30-2015)并结合生态防护结构特点,该类结构适宜在四川西部和南部、云南北部等竹类资源丰富的地区采用,适用于边坡比为1∶1~1∶1.5的路堑边坡,加固边坡类型主要为松散堆积体厚度为1~2 m的二元结构边坡或坡面破碎、易风化剥落的软质岩层边坡,每级边坡防护高度不超过6 m。

图2 竹制框架与锚杆结构设计示意图Fig.2 Design schematic diagram of bamboo frame and anchor rod structure
1.2 相似关系设计
以川西319国道沿线广泛分布的高度为10 m左右的下伏基岩-上覆浅层碎石土边坡为概化试验原型。以几何尺寸、地震动加速度、密度3个参数作为控制量,其相似常数分别为Cl=10、Cρ=1、Ca=1。根据相似理论和量纲分析法[15-16],可确定其余物理量的相似常数,见表1。

表1 模型试验相似常数Table 1 Similarity constants of model test
1.3 模型制作与测点布置
边坡模型在由钢板+型钢+角钢焊接制作的刚性模型箱内完成,模型箱的内部净空为2.0 m×1.5 m×1.6 m。通过在振动方向的模型后壁和前端分别内衬5 cm厚的聚苯乙烯泡沫板减小地震波的反射,同时在边坡模型纵向边界的两侧设置25 cm厚的聚苯乙烯泡沫板,且泡沫板外裹一层较为光滑的聚氯乙烯薄膜,以减小模型与模型箱侧壁的接触摩擦。
由于竹材的物质组成与木材等材料不同,难以找到同时满足密度相似和弹性模量相似的模拟材料。因此选择同为原竹加工而成的胶合竹为模拟材料,胶合竹为原竹的粗加工产品,保留了原竹的竹片单元,其强度和弹性模量显著低于细加工的重组竹。钢套筒采用预制的铝制构件模拟,并采用螺栓将相邻框架单元固定,如图3所示。锚杆采用M3螺纹杆模拟,锚杆穿过套筒的中心孔,并用螺栓固定牢靠。

图3 框架梁装配节点Fig.3 Assembly joint of frame beam
以碎石土作为浅覆盖层材料,模拟材料采用石英砂、细砂和黏土粉按一定配比混合搅拌而成。石英砂粒径范围为:1~2 mm和2~4 mm粒径各占25%,4~8 mm粒径占50%。控制土石质量比为1.6∶1,控制的碎石土密度为1.6 g/cm3。通过配比试验确定的模拟材料的质量配比为石英砂∶细砂∶黏土粉=1∶0.52∶1.08。通过直剪试验得到其黏聚力为7.2 kPa,内摩擦角为34°。边坡基岩采用红黏土进行模拟,在制作填筑时采用分层夯实并控制夯击次数,以保证基岩的整体性和硬度尽量与实际接近。为了模拟不同材料间的分界面并使得滑动面具有连续性,在碎石土和红黏土的交界面铺设一层细砂。碎石土分层填筑而成,并在预定高程处安置传感器,制作完成后的边坡模型如图4所示。

图4 振动台模型试验全貌Fig.4 Overview of shaking table model test
试验共设置13个加速度传感器和7个激光位移计,分别测定边坡坡面、基岩面和台面的加速度动力响应以及坡顶和坡面位移动力响应。所有传感器沿模型边坡中轴线及附近的纵剖面布设,边坡模型的传感器布置方案如图5所示。

图5 边坡模型的传感器布置(单位:cm)Fig.5 Sensor layout of slope model(Unit:cm)
1.4 地震波加载工况
试验采用人工波和天然波2种地震激励,其中人工波采用5、10、15 Hz频率的正弦波,天然波以汶川清屏波和El Centro波作为输入波原型。限于篇幅,图6仅给出了经时间压缩后幅值为0.6 g的汶川清屏波和El Centro波和试验加载时台面监测到的幅值为0.1 g的5 Hz正弦波。在试验过程中,按照输入波幅值由小到大、先天然波后人工波的顺序逐级进行加载。初始阶段先进行0.05 g低幅值白噪声扫描,用于测试边坡模型的初始动力特性,当天然波或人工波每级加载完毕后,也进行白噪声扫频,用于获得边坡模型的动力特性变化情况[17]。地震波加载方向为水平方向,试验加载工况顺序如表2所示。

表2 地震波加载工况Table 2 Loading scheme of seismic waves

图6 地震波加速度时程曲线Fig.6 Seismic acceleration time history curves
2 边坡加速度动力响应规律分析
2.1 加速度响应时域分析
为分析边坡不同高程的加速度响应,引入相对高度、加速度放大系数、Arias强度放大系数3个无量纲量。相对高度以边坡模型底面为基准,定义为各测点实际高度与边坡模型总高度的比值,边坡模型底面相对高度为0,边坡坡顶面相对高度为1。加速度放大系数和Arias强度放大系数均以振动台面实测加速度为基准,定义为边坡各测点响应峰值加速度(Arias强度)与振动台面上响应峰值加速度(Arias强度))的比值。
图7为3种地震波激振下PGA放大系数和Arias强度放大系数随高程的变化规律。3种地震波激振下,PGA放大系数和Arias强度放大系数沿高程均表现为非线性增大的特征,且变化趋势有相似之处,表现为折线中下段斜率较陡,而中上段斜率较缓,这表明大致以坡面中部(相对高程为0.65)为界,坡面中部以上的PGA放大系数比坡面中部以下增长更为显著。另外,从3条折线分布的紧密程度也可以看出,在坡脚附近,折线间分布较为紧密,地震波类型对PGA放大系数和Arias强度的影响不明显,而随着高程的增加,不同折线的间距越大,特别是在坡面中上部,3种地震波类型之间的差距非常明显,在0.1 g和0.3 g工况下的PGA放大系数和Arias强度放大系数均表现为汶川清屏波>El Centro波>5 Hz正弦波。

图7 不同地震波作用下坡面PGA放大系数和Arias强度放大系数随高程变化规律Fig.7 Variation of PGA amplification coefficient and Arias intensity amplification coefficient with elevation under different seismic waves
对比PGA放大系数和Arias强度放大系数随高程的变化曲线可知,二者在总体趋势上表现出较为一致的变化趋势,即放大系数随高程非线性增加,但也存在一定的区别。总的来说Arias强度放大系数折线较PGA放大系数折线更加光滑,数值是随着高程逐渐增加的,而非像PGA放大系数折线那样出现很多转折点,所以用Arias强度放大系数表示的高程放大效应能更好地看出趋势走向。但是也可以发现随着激振强度的增加,Arias强度放大系数在较低高程处表现出不同地震波之间差别较小,而此时的PGA放大系数则能很好地呈现不同地震波之间的差别,所以当地震动幅值发生改变时,PGA放大系数在揭示这一现象较Arias强度更有优势。
为探讨激振频率对加速度动力响应的影响,试验时加载了5、10、15 Hz这3个频率的正弦波,以0.1 g的正弦波工况为例进行加速度响应规律分析。图8为不同频率正弦波激励下坡面与基岩面的PGA放大系数和Arias强度放大系数随高程的变化规律。由图可知,坡面和基岩面上各测点的加速度响应变化规律较为相似,PGA放大系数和Arias强度放大系数都表现为:15 Hz正弦波>10 Hz正弦波>5 Hz正弦波,即随着正弦波频率的增加而增大。推测可能是由于边坡的自振频率与15 Hz最为接近,故15 Hz正弦波的响应最为强烈,这在后文频谱分析时得到了很好地验证解释。

图8 不同激振频率下坡面和基岩面PGA放大系数和Arias强度放大系数随高程变化规律Fig.8 Variation of PGA amplification coefficient and Arias intensity amplification coefficient with elevation under different excitation frequencies
以汶川清屏波的激振工况为例,研究激振强度对坡面加速度动力响应的影响。绘制PGA放大系数和Arias强度放大系数随激振强度的变化曲线,分别如图9和图10所示。由图可知,汶川清屏波激振下的PGA放大系数和Arias强度放大系数随激振强度增加呈现先增大后减小的趋势。对于PGA放大系数,在0.2 g激振之前,其随着激振强度增加而逐渐增加;在0.2 g之后,除了坡面中部以下A2测点和A1测点外,其余测点均表现出了逐渐减小的趋势。对于Arias强度放大系数,在0.3 g激振之前,其随着激振强度增加而逐渐缓慢增加;0.4 g时出现了陡降,而后随激振强度增加又有缓慢下降。不管是PGA放大系数还是Arias强度放大系数,其随激振强度的变化都表现了后期随着激振强度增加呈减小的趋势,分析后期PGA放大系数减小的可能原因是后期随着激振强度增加,坡体逐渐进入非线性塑性阶段,特别是浅覆盖层碎石土被部分振松或者滚落,刚度减小,阻尼增大,坡体对输入地震波的吸收能力增强所导致的。从图9(b)和图10(b)的三维图中也可以看出,随着激振强度的增加,坡面测点PGA放大系数曲面在激振强度为0.3 g时存在一个下凹点,而Arias强度放大系数由于在较低高程处表现出各测点之间响应差异较小,因此没有表现出随激振强度的突变。随着边坡高程的增加,Arias强度放大系数曲面在坡顶附近上凸明显,呈现出明显的高程放大效应。可以推断出Arias强度放大系数对此类结构加固边坡的高程放大效应影响较大,PGA放大系数对动力响应随地震动幅值的变化影响较大。

图9 汶川清屏波激振下各测点PGA放大系数随激振强度变化规律Fig.9 Variation of PGA amplification coefficient of each measuring point with excitation intensity under Wenchuan wave excitation

图10 汶川清屏波激振下各测点Arias强度放大系数随激振强度变化规律Fig.10 Variation of Arias intensity amplification coefficient of each measuring point with excitation intensity under Wenchuan wave excitation
通过查阅与本研究试验模型相似的振动台模型试验,将文中试验结果与已有文献结果[18-19]进行对比分析,以期评估“竹制框架+锚杆”的加固效果。选取输入地震波峰值0.2 g为对比工况,一是因为0.2 g为两篇文献中共有的加载工况,二是边坡体在0.2 g的地震波激振下均处于弹性阶段,便于进行对比分析。图11为有支护和无支护边坡的坡面加速度放大系数随相对高度的变化规律。可以看出生态框架防护边坡的坡面加速度放大系数整体上要小于两个无支护边坡,这是由于竹制框架为装配式结构,柔性连接节点耗散了部分地震波能量,且重组竹材料也具有良好的弹性变形能力,从而使得边坡整体的地震响应降低。

图11 有支护和无支护边坡的加速度放大系数与相对高程的关系曲线Fig.11 Relationship between acceleration magnification coefficient and relative elevation of supported and unsupported slopes
2.2 加速度响应频谱特征分析
基于蒋良潍等[20]介绍的方法,利用Matlab的tfestimate函数来计算边坡不同高度、不同加载阶段的传递函数虚频特性曲线,从而得到边坡的各阶自振频率,虚频特性曲线从频域的角度描述了边坡系统对输入地震波的传递特性,可定量表达边坡模型的动力特性。图12为边坡在初始白噪声工况和结束白噪声工况下的传递函数虚频特性曲线。由图可知,在本试验所考虑的频率范围内,通过传递函数虚频特性曲线在水平向识别出了明显的4阶自振频率。初始状态下,边坡的4阶自振频率分别为15.14、33.20、38.57、45.90 Hz。而随着地震波加载,在结束状态下,边坡的4阶自振频率均有所下降,变为14.16、30.27、36.62、43.95 Hz,其中第1阶自振频率相较于其余3阶自振频率下降最小。这也可以解释时域分析中为何15 Hz的正弦波激振程度最为强烈,其原因是15 Hz的正弦波其频率与边坡的第1阶自振频率最为接近,而10 Hz和5 Hz分别次之,因此表现出正弦波随激振频率增加而响应逐渐增加的性质。另外,随着激振进行,边坡的4阶自振频率均有所降低,这表明逐级重复加载具有损伤累积效应,边坡结构随着试验的进行逐渐变得松散,刚度下降,剪切模量降低,阻尼比增大,这种动力特性的变化会使得后续工况的动力响应减小,应特别注意。动力特性的变化也印证了时域分析中在加载中后期随着激振强度增加而PGA放大系数呈减小的规律。主要原因是坡体经历地震波作用逐渐损伤和浅覆盖层的逐渐松动滑落而使其刚度减小,土体非线性特征加强,阻尼比增大,坡体对输入地震波的吸收能力增强,因此会出现后期PGA放大系数呈减小的规律。

图12 白噪声激振下的传递函数虚频特性曲线Fig.12 Imaginary frequency characteristic curve of transfer function excited by white noise
为研究浅覆盖层边坡对地震波传播过程中频谱成分的影响规律,选取0.1 g的汶川清屏波作为研究工况,分析坡面上各测点的加速度傅里叶谱响应随高程的变化规律,坡面典型测点的加速度傅里叶谱响应如图13所示。
由图13可知,0.1 g汶川清屏波激振下,台面测得的输入地震波傅里叶谱在整个频段范围内的幅值都较大,地震波在边坡内由下向上传播时,主要在4个频段得到了较为显著的选择性放大,分别为14.61~17.21 Hz频段、33.06 Hz频段、38.64~40.50 Hz频段以及47.65 Hz频段,这4个频段分别与前述识别出的边坡4阶自振频率对应,表明地震波经边坡介质传播后,频谱特性发生了改变,且变化具有在边坡自振频率附近选择性放大的特点。另外,对比不同高程点的傅里叶谱,可以发现,坡面下部A1和A2测点的体现出的选择性放大效应不太明显,而中上部的A5~A7测点则非常明显,这也与时域分析中加速度放大程度在坡面中上部和坡面下部存在差异相吻合。

图13 0.1 g汶川清屏波激振下坡面不同测点傅里叶谱Fig.13 Fourier spectra of typical measuring points on slope surface under 0.1 g Wenchuan wave excitation
为研究不同激振强度下地震波的频谱成分变化规律,以汶川清屏波激振工况为例,分析台面和坡面A7测点在不同激振强度下的频谱成分变化规律,各测点经平滑后的加速度傅里叶谱响应如图14所示。

图14 汶川清屏波激振下测点加速度傅里叶响应谱随激振强度变化规律Fig.14 Variation of acceleration Fourier response spectra with excitation intensity under Wenchuan wave excitation
从图14中可以看出,对于台面测点,不同激振强度下的傅里叶谱形状基本一致,且呈现出随激振强度增加而傅里叶谱幅值也相应增加的规律,各激振工况下的谱峰值对应的频率基本一致。对于坡面A7测点,不同激振强度下的傅里叶谱形状呈现出较大差异,0.1 g时的谱形状表现为前半频段幅值小后半频段幅值大的特点,而随着激振强度增加,傅里叶谱在前半频段内出现多个幅值相当的峰值点,这表明随着激振强度增加,边坡对低频的放大作用逐渐增加;还可以看到随激振强度增加,谱峰值整体向频率轴负方向移动,且激振强度越大,移动越明显,这是因为随着地震动的持续加载,边坡的自振频率降低,导致了谱峰值跟随自振频率向左移动。此外,从傅里叶谱的幅值上看,其随激振强度增加大体呈现增加的趋势,但不同频段的增长幅度有差异,总体来说,在30 Hz以内的频段增长较大,而大于30 Hz的高频段增长不明显,谱幅值一直处于较低水平。在0.3 g激振下,测点30~40 Hz频段范围内的谱幅值增长较大,甚至超过了0.6 g激振下的谱幅值。综上所述,随着激振强度增加,除个别频段外,谱峰值都表现为逐渐增大,并且由于自振频率降低,加速度响应的傅里叶谱卓越频率也相应有所下降。
为进一步分析边坡的动力响应特性与动力响应规律的内在联系,分别计算坡面各测点与台面的傅里叶谱比值,计算时需先将傅里叶谱进行平滑再做比值。图15为0.1 g的汶川清屏波和El Centro波激振下,边坡坡面A1~A7测点与台面的加速度傅里叶谱比曲线。由图可知,利用坡面测点与台面测点的谱比曲线也能较好地识别出边坡的各阶自振频率,可近似反应边坡体对激振波的传递特性。与前述用白噪声数据求传递函数虚频特性曲线方法识别出的结果基本一致,最大误差在1.2 Hz以内。此外由坡面各测点的谱比值大小来看,高程越大,谱比值越大并且增长也越快,也体现了边坡加速度响应沿高程的非线性放大效应。
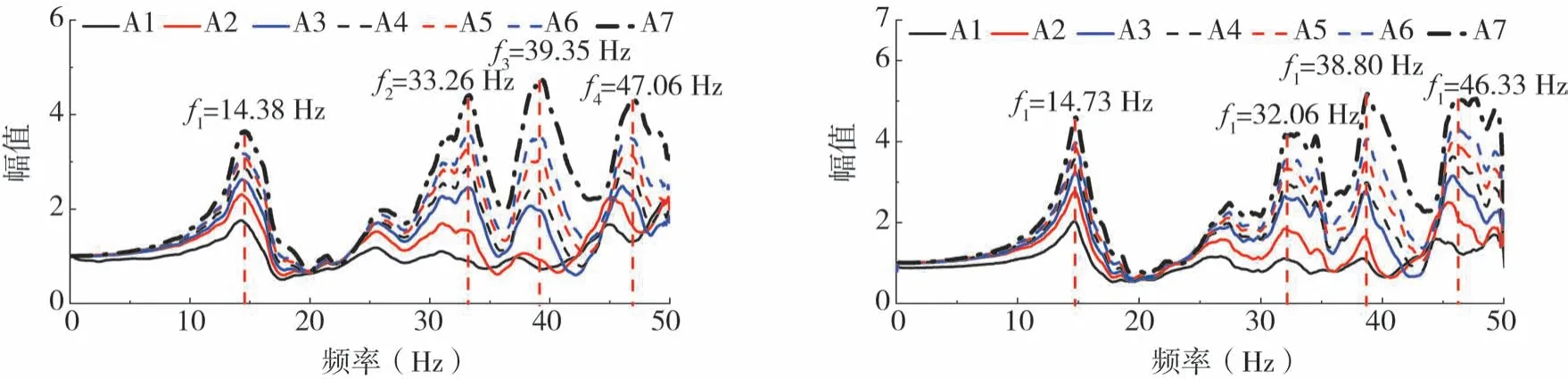
图15 0.1 g汶川波和El激振下的傅里叶谱比曲线Fig.15 Fourier spectrum ratio curves under 0.1 g Wenchuan wave and El wave excitations
2.3 加速度响应时频谱特征分析
本节采用地震信号处理中广泛采用的希尔伯特-黄变换(Hilbert-Huang Transform,HHT)方法,从时频域角度分析边坡动力响应特征,以期同时反应加速度响应信号的频率和时间信息。HHT的主要步骤分为2部分:首先是经验模态分解(empirical mode decomposition,EMD),可以将信号分解成有限的本征模态函数IMF及残余值r;然后对各本征模态函数进行Hilbert变换,得出相应加速度信号的时-频-幅值(能量)谱。
为研究浅覆盖层边坡对地震波传播过程中时频谱成分的影响规律,选取0.1 g的汶川清屏波作为研究工况,分析浅覆盖层边坡不同高程处测点的Hilbert-Huang能量谱的变化规律。限于篇幅,仅给出台面、基岩面、坡面上典型测点的Hilbert-Huang能量谱,如图16所示。
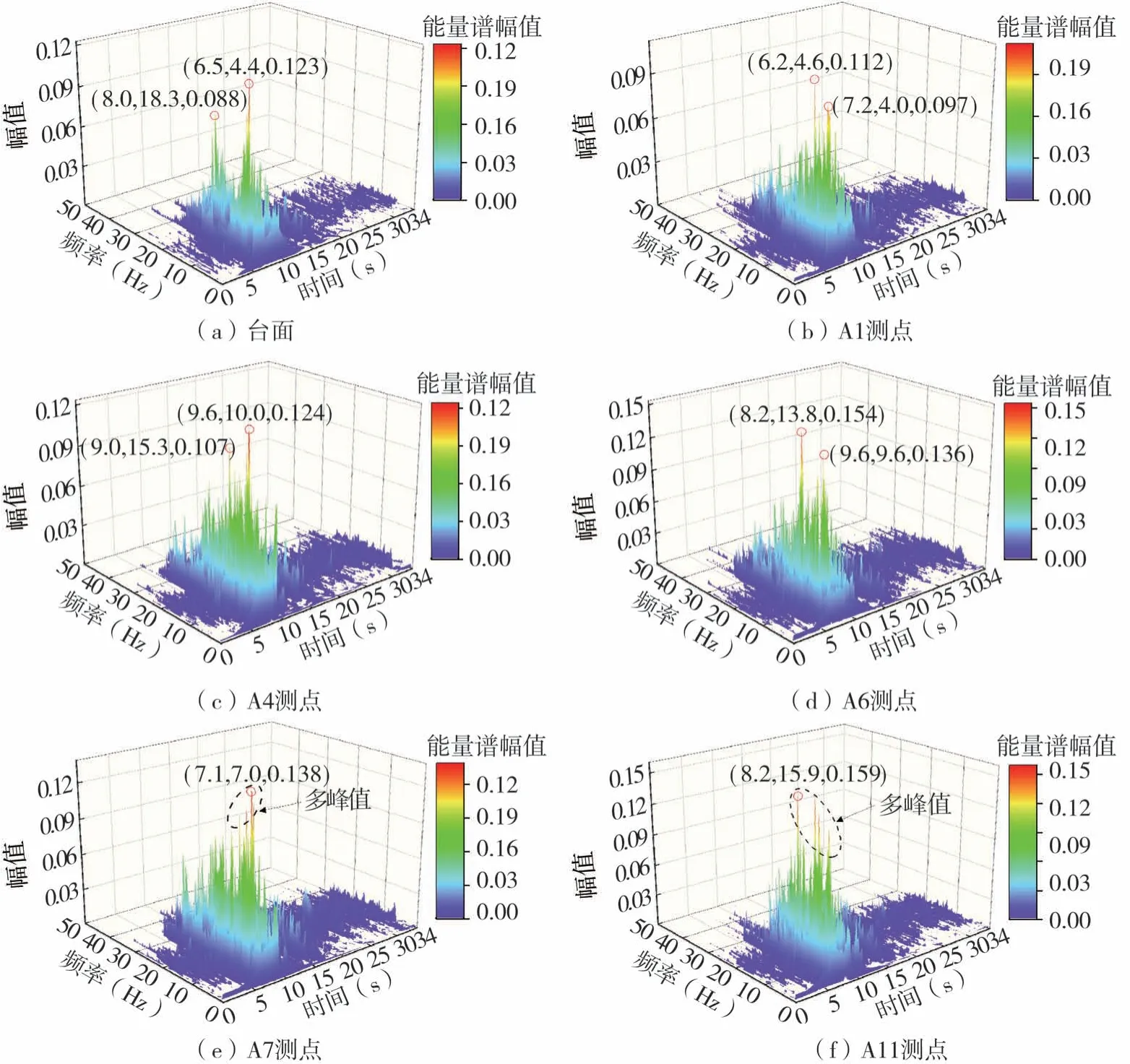
图16 0.1 g汶川清屏波激振下典型测点的Hilbert-Huang能量谱Fig.16 Hilbert-Huang energy spectrum of typical measuring points under 0.1 g Wenchuan wave excitation
汶川清屏波激振下,坡面各测点的加速度Hilbert-Huang时频谱形状与台面差别较大,台面时频谱呈“双峰值”特征,双峰间的时间相近,但频率相差较大,分别为4.4 Hz和18.3 Hz,而坡面测点的时频谱形状逐渐由“双峰值”特征转变为“多峰值”特征,且各峰值出现的时间和频率都较台面更加聚拢。随着高程增加,时频谱峰值部分的频率成分变得更加丰富,并且峰值总体上有增大趋势,但是由于高程增加时,频率逐渐丰富的时频谱峰值部分分散了一部分能量,因此会出现个别峰值减小的情况。此外,从峰值出现的时间和频率上看,均有一定变化,其中时间上相差较小,基本都处于6~10 s,位于强震段区间内,而频率上从台面及A1测点的5 Hz左右逐渐增大到坡面上部A4~A7测点的7~10 Hz,这表明随高程增加,地震波能量有由低频向高频转移的趋势,这主要与边坡的地形效应有关。
对比分析坡面A7测点和与之垂直对应的基岩面A11测点的Hilbert-Huang能量谱可以发现,两者在形态上很相似,且均呈现“多峰值”特征,但是“多峰值”段在时间和频率上的分布范围有差别,在时间上较为接近,都在7~8 s左右,在频率上,A11测点的峰值对应的频率为15.9 Hz,而A7测点的峰值对应频率为7.0 Hz,且后者“多峰值”段在频率轴上分布范围更小,表明地震波经浅覆盖层传播后,能量被一定程度聚拢,能量分布的频率范围变小,并且能量在传递时有由高频向低频转移的趋势。从能量谱的峰值来看,A11测点的峰值小于A7测点的峰值,表明地震波经浅覆盖层传播后能量有一定损失。这也与地形效应以及非线性效应有关,由于边坡土体随着激振强度的增加和地震波加载工况的重复进行,土体损伤加剧,浅覆盖层整体性被破坏从而发生局部的松动掉块,致使浅覆盖层刚度降低,土体非线性特征增强,阻尼比增大,从而在与支护结构的相互作用下,表现出低频放大和高频滤波的作用,土体非线性效应起到主导地位。
3 边坡位移响应与宏观破坏现象
3.1 边坡位移响应规律分析
为探讨坡顶竖向位移响应峰值随激振强度的变化规律,图17给出了汶川清屏波和El Centro波激振下D7监测点竖向位移响应峰值与激振强度的关系曲线。由图可知,2种地震波激振下的坡顶位移响应峰值均与输入波激振强度呈正相关变化。汶川清屏波激振时,坡顶位移峰值在0.4 g以前随激振强度增加较快,而后趋于平缓。El Centro波激振时,坡顶位移峰值随激振强度呈波动型变化特征。汶川清屏波激振时坡顶的位移峰值始终大于El Centro波激振时的位移峰值,并且在激振强度较小时,二者差距很小,在0.2 g以后二者差距比较明显。
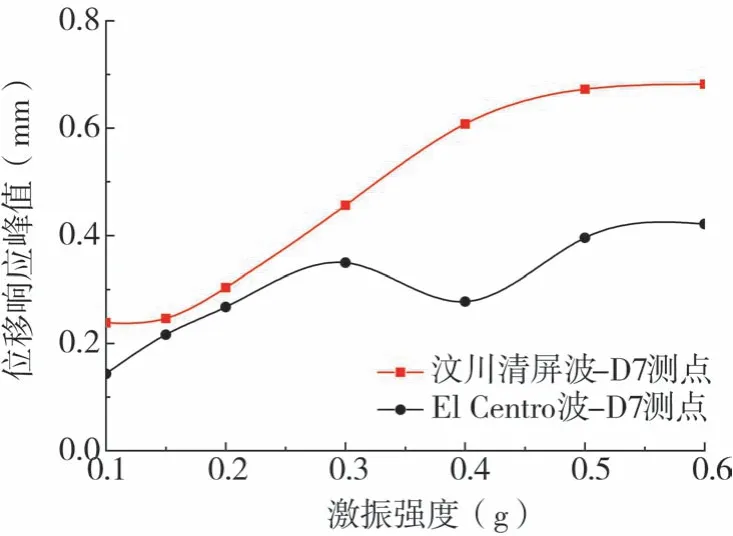
图17 坡顶竖向位移响应峰值随激振强度变化规律Fig.17 Variation of peak vertical displacement at the top of slope with excitation intensity
以汶川清屏波和El Centro波激振为例进行分析坡面的动位移响应规律。图18为3种地震波激振下坡面中部D4测点和坡面上部D6测点的水平位移响应峰值与激振强度的关系曲线。由图可知,2种地震波激振下的坡面不同部位的水平位移响应峰值均与输入波激振强度大致呈正相关变化。在汶川清屏波和El Centro波激振下,坡面上部的位移响应峰值随激振强度的增加呈波动型增大趋势,而坡面中部的位移响应峰值随激振强度的增加呈近似线性增大趋势。坡面上部的位移响应峰值明显大于坡面中部的位移响应峰值。因此,在用框架结构防护浅覆盖层边坡时应注意加固坡肩和坡顶处的岩土体。

图18 坡面不同部位的水平位移响应峰值随激振强度变化规律Fig.18 Variation of peak vertical displacement at different parts of the slope with excitation intensity
3.2 宏观变形破坏现象
通过分析汶川清屏波、El Centro波和正弦波激励后的各工况边坡变形照片,将边坡的宏观变形破坏现象描述如下:(1)加载完0.3 g的El Centro波后,边坡模型未见明显变形迹象,仅有粗颗粒滚落堆积于框架梁横梁处,如图19(a)所示;(2)加载完0.3 g的15 Hz正弦波加载后,边坡模型在坡肩处首先出现局部掉块现象,坡体上部左侧边界处也有小范围的掉块,坡顶和坡面有更多粗颗粒被震松,滑落堆积到横梁处,坡脚也有少量碎石滚落,边坡形态如图19(b)所示;(3)加载完0.6 g的El Centro波后,坡肩处掉块区持续加大,已扩展到坡顶处,框格内和边界处的无防护区被震裂、松弛,坡面浅覆盖层发生大面积的脱落,松散土体顺坡面溜塌并堆积于框架梁横梁和坡脚处,但浅覆盖层整体仍保持稳定,震后整体边坡形态如图19(c)所示,图19(d)为局部放大图。总结以上破坏现象可知,浅覆盖层边坡体的震害主要发生在覆盖层顶部和坡面无防护部位,破坏发展过程可描述为:坡面中上部粗颗粒滚落→坡肩局部剥落掉块→坡面覆盖层被震裂松弛,框格内局部掉块→坡顶被震散坍塌、坡面较大面积溜塌。

图19 (续)Fig.19(Continued)

图19 不同激振强度下浅覆盖层边坡的宏观破坏现象Fig.19 Macroscopic failure phenomenon of shallow overburden slope under different excitation intensities
4 结论
(1)坡面和基岩面上的PGA放大系数和Arias强度放大系数随高程和激振强度的增加在总体趋势上表现出较为一致的变化规律,即随着高程增加而呈非线性增加的趋势,随激振强度增加呈现先增大后减小的趋势。Arias强度放大系数折线较PGA放大系数折线更加光滑,用Arias强度放大系数表示的高程放大效应能更好地看出趋势走向,而在地震波参数发生改变时,PGA放大系数在揭示这一现象较Arias强度更有优势。
(2)基于传递函数虚频特性曲线,在水平向识别出了边坡的4阶自振频率。初始状态下,边坡的4阶自振频率分别为15.14、33.20、38.57、45.90 Hz。随着地震波加载进行,边坡的4阶自振频率均有所下降,并且通过坡面与台面的傅里叶谱比计算得到了相互验证。由不同地震波类型和不同高程的加速度傅里叶谱分析可知,边坡对与其自振频率接近的地震波成分敏感,放大效应明显,表现出选择性放大作用。
(3)当地震波沿浅覆盖层表面向上传播时,Hilbert-Huang能量谱表明随边坡高程的增加,地震波能量谱幅值增大,高程对地震波能量具有聚拢作用,使其峰值附近的频率成分更加丰富,地震波能量分布有由低频向高频转移的趋势。当地震波从基岩面垂直传播到坡面时,地震波也存在聚集效应,能量在频率上的分布范围变小,但有由高频向低频转移的趋势,地震波在经浅覆盖层传播后有一定的能量损失。
(4)2种地震波激振下的坡顶竖向位移响应峰值均与地震波强度呈正相关变化,坡面水平位移响应峰值均与边坡高程呈正相关变化。浅覆盖层边坡体的震害主要发生在浅覆盖层顶部和坡面框格内,变形破坏过程可归结为:坡面中上部粗颗粒滚落→坡肩局部剥落掉块→坡面被震裂松弛、局部掉块→坡顶震散坍塌、坡面无防护区较大面积溜塌。在高烈度区使用该结构时应结合植被防护技术,对坡面和坡顶处进行浅层加固。

