分块初等变换在判定抽象矩阵可逆性中的应用

薛维顺

（山西晋中理工学院，山西晋中 030600）

矩阵是线性代数最重要的工具之一，在计算和处理数据方面都有非常重要的作用。矩阵的逆是众多学者研究的重要课题。分块矩阵由于其抽象性，研究难度相对较大[1-6]。杨欣芳[5]给出了广义初等变换和广义初等矩阵的定义并对简单分块矩阵的广义初等变换进行验证。张新育[2]定义了分块初等变换和分块初等矩阵，给出了相关性质并对抽象矩阵的逆和秩进行了研究。孙霞[3]和成立花[6]利用分块初等变换对两个互素矩阵多项式的秩进行了研究。刘俊同[4]对分块矩阵行列式对行列式进行了推广。继续利用分块矩阵的初等变换对抽象矩阵的可逆性进行研究，给出三类抽象矩阵可逆性的判定，并得出应用。文中用到的数字都是实数。

1 相关概念和性质

定义1将m×n矩阵A做如下分块

（1）用一个可逆矩阵左(右)乘分块矩阵的某一行(列)块；

（2）分块矩阵的某一行(列)块左(右)乘一个矩阵加到另外一行(列)块；

（3）交换某两行(列)块。

分块矩阵的行初等变换与列初等变换统称为分块初等变换[2]。

定义2分块初等矩阵是分块单位矩阵

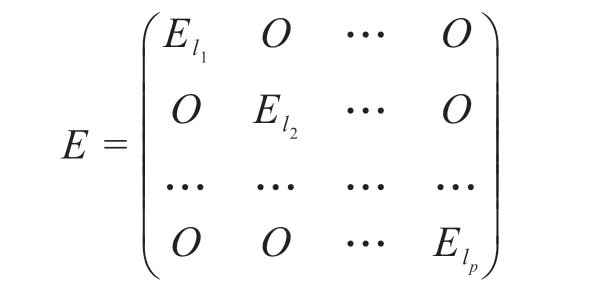
经过一次分块初等变换所得到的分块矩阵。其中Elr为lr阶单位矩阵[2]。

性质1分块初等变换不改变矩阵的秩[3]。

性质2设A是m阶方阵,B是n阶方阵，则=R(A) +R(B)[3]。

2 主要结论及证明

多个数为零的情形与一个数为零的情形证明过程类似。

综上，对任意的实数ai(i=1,2,…,n)，n阶方阵C总可逆。

3 应用举例

例1已知A,B,A+B均为n阶可逆方阵，证明A-1+B-1也可逆。

在证明A-1+B-1可逆的时候，通过定义找到A-1+B-1的逆矩阵进行了证明。这种证明一般很难通过定义判定A-1+B-1的可逆性。如果利用分块矩阵的初等变换能很容易判定A-1+B-1的可逆性。

证明

例2若n阶矩阵A满足A2-2A-4E=O,证明:A+E可逆。

以往证明此类抽象矩阵可逆时一般采用“凑因式”的方法化为AB=E的形式来判定可逆。通过分块矩阵的初等变换能开拓学生的解题思路，从而进一步培养学生的发散思维能力。是定理1 中k=的情形，故可逆。

利用分块矩阵的初等变换不仅可以判断矩阵可逆，也可以很巧妙的对行列式进行计算。在2020 年的研究生入学考试（数一）中有一道对行列式的计算。如果按照常规思路就是“化零降阶”或者直接按行按列展开，计算量相对较大。如果采用分块矩阵的初等变换会简化计算。

可以看出分块初等变换不仅在判定抽象矩阵的可逆性中作用巨大,在计算行列式中也应用广泛。