RIS辅助无线系统中基于压缩感知的稀疏度自适应级联信道估计方法研究

米连锋 何雪云 孙林慧

（南京邮电大学通信与信息工程学院，江苏南京 210003）

1 引言

近年来，可重构智能超表面（Reconfigurable Intelligent Surface，RIS）技术逐渐引起了众多学者的研究，通过布置大量的RIS 无源元件来人为改善无线通信过程中的通信环境［1］，提高信道容量，扩大覆盖范围［2］，被公认为是6G 潜在的通信技术之一［3］。RIS 元件都是无源器件，不能发射、接收或处理任何导频信号［4］，并且RIS 通常由数百个元素组成，需要估计的信道维度比常规通信系统大很多，因此信道估计是RIS 辅助无线通信系统的一个关键挑战［5］。CS 技术能同时对数据进行采集和压缩［6-7］，常用于信道估计［8］。已经有学者针对RIS 辅助无线通信系统级联信道估计问题提出了基于CS的估计方法，如RSS-OMP（Row-Structured Sparsity Orthogonal Matching Pursuit，RSS-OMP）算法［9］、DS-OMP（Double-Structured Orthogonal Matching Pursuit，DS-OMP）算法［10］等。RSS-OMP 算法是基于矩阵行结构稀疏特性的方案，而DS-OMP算法是在前者的基础上，利用级联信道的双结构稀疏特性即行稀疏特性和列稀疏特性，进一步提高算法估计性能。然而，这些算法都存在一个公共的问题，均假设通信信道的稀疏度信息是已知的，而实际应用中这些参数很难准确获取，这就使得算法在实际系统中的应用受到极大的限制。

因此，本文提出了一种自适应双结构稀疏正交匹配追踪算法（Adaptive Double-Structured Orthogonal Matching Pursuit，ADS-OMP），即在已有DS-OMP算法利用双结构稀疏特性的基础上，通过设计合理的判决准则和迭代阈值完成公共非零行支撑集和公共非零列支撑集的估计，使其能在行稀疏度和列稀疏度均未知的情况下完成信道估计。仿真结果表明，本文提出的ADS-OMP 算法与DS-OMP 算法估计性能一致，算法复杂度略微提升。

2 系统模型

对于如图1 所示的上行链路RIS 辅助的移动无线通信系统，我们考虑包含M个天线的基站BS（Basic Station，BS），由N元件组成的RIS 来服务K个单天线用户。令hd，k∈CM×1表示第k个用户与基站之间的直接信道，G∈CM×N表示RIS和BS 之间的信道，hr，k∈CN×1表示第k个用户与RIS 之间的间接信道，则在基站处接收到的信号y∈CM×1可表示为：

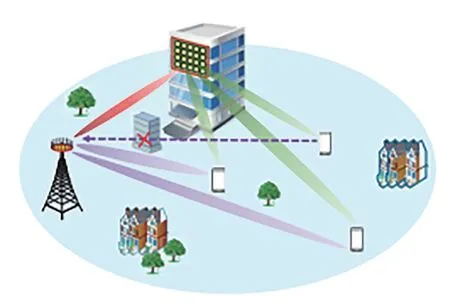
图1 RIS辅助无线通信系统实例Fig.1 RIS Assisted Wireless Communication System Instance

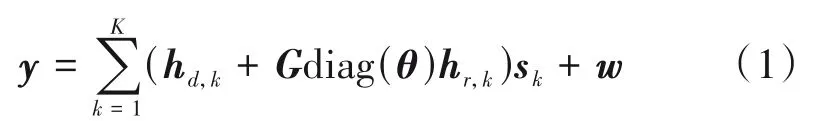
sk表示第k个用户的发送信号，θ=[θ1，θ2，…，θN]T表示在RIS 处的反射向量，其中θn表示第n条路径的反射系数，w∈CM×1表示在基站处的接收噪声。采用Saleh-Valenzuela信道模型［11］，G可表示为：

其中LG表示BS 和RIS 之间的路径数和分别表示第l1路径上考虑路径损耗的复增益、BS 方位角仰角和RIS 方位角仰角。同理，信道hr，k可以表示为：

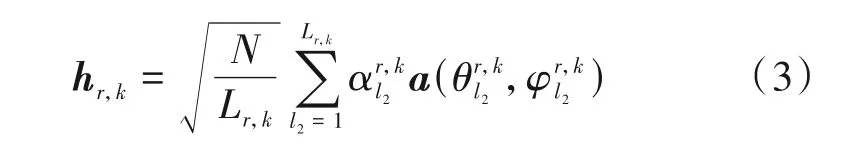
其中Lr，k表示第k个用户和RIS 之间的路径数分别表示第l2路径上考虑路径损耗的复增益和RIS的方位角仰角。a(θ，φ)∈CN×1和b(θ，φ) ∈CM×1分别表示与BS 和RIS 相关的归一化阵列方向向量。令N=N1×N2，a(θ，φ)可表示为：

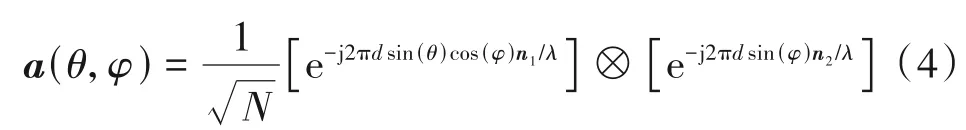
其中n1=[0，1，…，N1-1]和n2=[0，1，…，N2-1]，λ为载波波长，d为天线间距，通常取d=λ/2。

让Hk=Gdiag(hr，k) ∈CM×N表示第k个用户 和BS 之间通过RIS 的级联信道，此时接受信号y可表示为：

在本文中，我们假设BS和用户之间的直接信道hd，k对于BS 是已知的，这可以很容易地采用传统的信道估计方法进行估计。因此，我们只需要关注级联信道的估计问题，即级联信道Hk的估计问题。采用虚拟角域的表示法，Hk可分解为：

∈CM×N表示角域级联信道，UM∈CM×M和UN∈CN×N表示BS和RIS之间的酉矩阵。由于在BS和RIS附近的散射是有限的，因此角域级联信道k具有稀疏性。通过采用广泛使用的正交导频传输策略，所有用户在Q个时隙上通过RIS 将已知导频符号发送到BS以用于上行链路信道估计。具体地，在第q（q＝1，2，…，Q）个时隙中，移除直接信道的影响后，第k个用户到BS 的有效接收信号yk，q∈CM×1可以表示为：

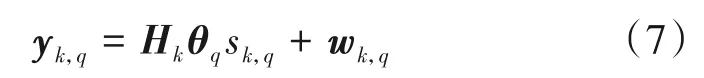
在导频传输Q个时隙后，假设sk，q=1，得到Q×M的总体测量矩阵Yk=[yk，1，…，yk，Q]，Yk可表示为：

从而将RIS辅助无线通信系统中级联信道估计问题转化为在已知有效测量矩阵和传感矩阵的情况下恢复角域级联信道的问题。

3 RIS辅助无线通信系统级联信道估计

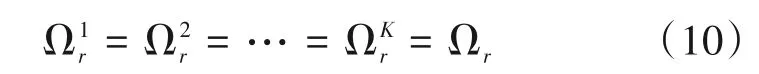
另外，由于部分共同散射体的存在，RIS 与不同用户之间的信道hr，k可能拥有部分相同的路径与角度，具有列结构稀疏特性。表现为：

4 仿真结果和分析

本文所提出的ADS-OMP 算法是在DS-OMP 算法的基础上改进而来，为了能够充分比较两者之间的性能差异，实验时采取与文献［10］相同的仿真环境，考虑用户数为K=16，BS 的天线数为M=64(M1=8，M2=8)，RIS 的元件数为N=256(N1=16，N2=16)，RIS和BS之间的路径数为LG=5，任意用户和RIS 之间的路径数为Lr，k=8，时隙数取Q=48，分别取Lc=4、Lc=6 来进行模拟仿真，以标准化均方误差（Normalized Mean Square Error，NMSE）作为估计性能的衡量标准，一轮仿真200 次，取NMSE 平均值。本文算法仿真时均假设LG、Lr，k和Lc未知，而文献［10］中DS-OMP 算法默认这些参数已知。

图2是当Lc=4时三种算法性能曲线图，可以看出，随着信噪比的不断增大，RSS-OMP 算法、ADSOMP算法和DS-OMP算法的NMSE值均随之减小，但ADS-OMP 算法和DS-OMP 算法NMSE 值比RSS-OMP算法低1.5 dB，这是利用双结构稀疏特性带来的性能提升。ADS-OMP 算法和DS-OMP 算法的信道估计性能均随信噪比的增大而提升，两者估计性能一致。

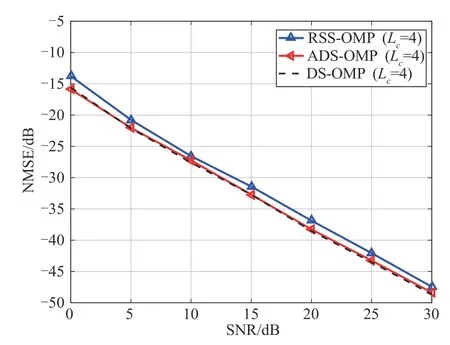
图2 Lc=4时信道估计性能曲线图Fig.2 Channel Estimation Performance Curve at Lc=4

如图3 所示，当Lc=6 时，ADS-OMP 算法和DSOMP算法的NMSE值比ADS-OMP算法低2.5 dB，较Lc=4 有所提升，这表明随着Lc的增大，利用双结构稀疏特性带来的性能提升愈加明显。ADS-OMP 算法和DS-OMP算法估计性能一致。

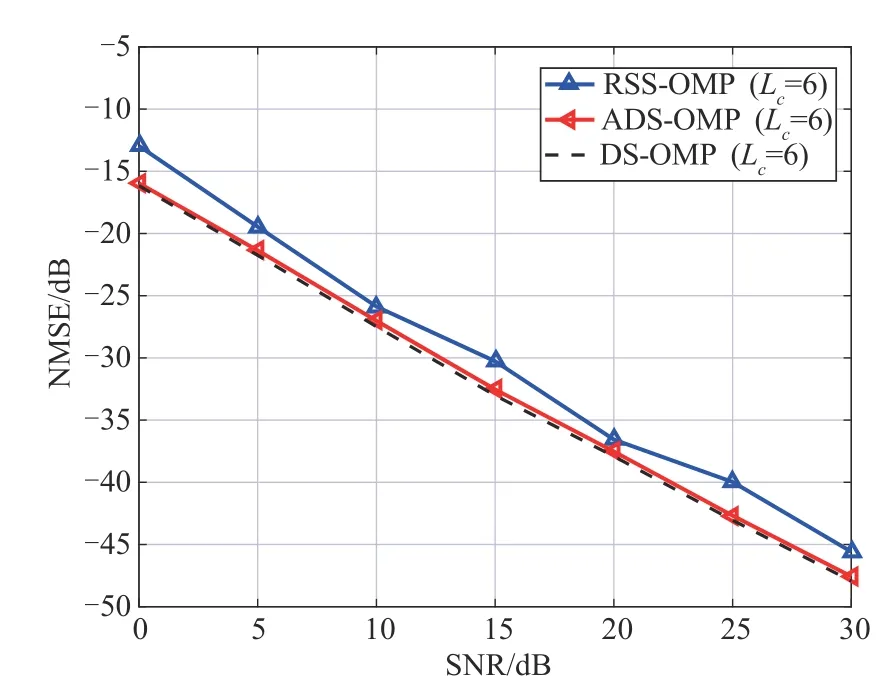
图3 Lc=6时信道估计性能曲线图Fig.3 Channel Estimation Performance Curve at Lc=6

由表1 可以看出，在运行时间上，ADS-OMP 算法单次平均耗费时间为0.213 s，DS-OMP 算法单次平均耗时0.122 s，这表明ADS-OMP 算法整体复杂度高于DS-OMP 算法。原因是DS-OMP 算法忽略了LG、Lr，k和Lc等参数获取过程中付出的算法复杂度，而将这些参数默认已知，由于传播环境的变化这些参数在实际中很难轻易获取且可能是变化的，因此算法实用性低；ADS-OMP 算法复杂度上的提升主要来源于这些参数的估计。ADS-OMP 算法以增加一定的算法复杂度去除对难以获得的先验参数的依赖，增加算法的实用性，我们认为这是有意义的。

表1 平均运行时间Tab.1 Average run time

总而言之，在估计性能方面，随着信噪比的提升，ADS-OMP 算法和DS-OMP 算法的估计性能呈直线式上升，且都随公共路径数Lc的增大而有所提升，两种算法的估计性能曲线基本重合。从运行时间上可以看出，ADS-OMP 算法整体复杂度较DSOMP 算法复杂度有所增加，但是相对于DS-OMP 算法，ADS-OMP 算法不需要LG、Lr，k和Lc等先验知识，实用性更强。

5 结论

本文提出了一种基于压缩感知技术针对RIS辅助移动通信系统级联信道的自适应信道估计算法，该算法在文献［10］提出的DS-OMP算法基础上设计合理的判决准则和迭代阈值使得算法能够在角域级联信道的行稀疏度和列稀疏度均未知的情况下完成级联信道估计。仿真结果表明，本文提出的ADS-OMP 算法与DS-OMP 算法估计性能一致，其算法复杂度较DS-OMP 算法略微提升，但仍处在同一数量级上。本文提出的ADS-OMP 算法由于不需要更多的信道稀疏度等先验条件，实用性更强。