改进的基于压缩感知的自适应波束形成算法

王建，王松，丁其洪，樊书辰，江锋，张宏伟

（1.中国航天科工集团8511研究所，江苏 南京 210007；2.中国人民解放军32086部队，江苏 南京 210018）

0 引言

为了在保持口径不变的前提下尽可能地减少阵元与射频前端数量，人们提出了多种有效降低稀布阵旁瓣的方法，常见的有：遗传算法［1］、蚁群算法［2］、粒子群算法［3］和模拟退火算法［4］等。但是以上算法都是只针对某个特定的方向图进行优化布阵，当波束扫描、方向图形状改变或者自适应干扰抑制进行时，波束性能会明显恶化。

近年来，压缩感知理论的发展突破了传统的奈奎斯特采样定理。压缩感知理论［5-6］指出，只要信号是稀疏的或可压缩的（即在某个变换域上是稀疏的），那么就可以用一个与变换基不相关的采样矩阵将变换所得的高维信号投影到一个低维空间上，然后通过求解一个优化问题，从这些少量的投影中以高概率重构出原信号。根据压缩感知的这一特性，可以利用少量的采样信号先对阵列信号进行重构，得到满阵时各通道的数据，然后利用重构的信号进行波束形成。这样形成的波束图与满阵时候波束性能几乎相同，能够自适应地抑制干扰，具有波束旁瓣低、指向误差小、干扰方向零陷深且没有栅瓣等优点。目前压缩感知重构算法很多，但是计算量都相对较大，难以满足实时信号处理要求。近年来，针对压缩感知的快速重构也有了大量的研究。文献［7］提出了一种快速最优正交匹配追踪（Fast OOMP）算法，该算法在原先OOMP基础上，利用上一次的迭代结果计算当前的迭代结果，从而减少计算量；文献［8］提出了一种快速连续的压缩感知算法，利用低秩矩阵填充的特性，进行信号恢复，在保证矩阵半正定的过程中，用数学方法进行简化从而减少计算量；文献［9］提出了基于光滑L0范数的快速重构算法；文献［10］利用信号之间的联系提出了基于最小二乘的信号重构；文献［11］提出了一种基于离散余弦变换的快速重构算法。

本文通过对联合正交匹配追踪（J-OMP）算法［12-13］的研究，结合阵列信号处理中信号角度信息随快拍变化较慢这一特点，提出了一种改进的基于多快拍的自适应栅格调整的优化算法，该算法不但恢复效果优于J-OMP，而且在计算量上也大大减少。

1 信号模型

对于N个阵元的阵列，假设有K个远场回波信号入射到天线阵面上，阵列天线各阵元的接收信号可用一个N维的向量X（t）表示：

式中，V（t）=［v1（t），v2（t），…，vN（t）］T为由各个阵元通道的高斯白噪声组成的向量，sk（t）为第k个回波信号。对于间距为d均匀线阵，导向矢量ak可以表示为：

式中，λ为工作波长，uk=sin（θk），θk为第k个信号的回波方向。

根据|sin（θi）-sin（θi+1）|=2/N，将-90°～90°的空域N等分，得到ui，i=1，2，…，N。用这N个导向矢量构建变换矩阵A：

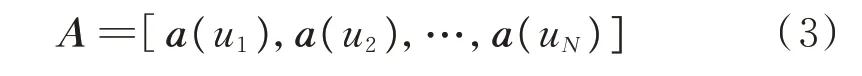
压缩采样不是直接测量X（t），而是设计一个与A不相关的M×N（M＜＜N）维采样矩阵Φ。测量X（t）在Φ上的投影向量Y（t），即：

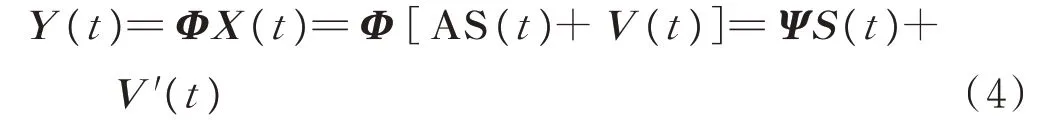
式中，V′（t）=ΦV（t）是系统压缩采样之后的噪声，采样矩阵Φ表示天线对空域信号的压缩采样方式。矩阵Ψ=ΦA是一个M×N的矩阵，称为观测矩阵。理论研究表明，当观测矩阵Ψ满足限制等容性（RIP）［14］条件时，便可通过求解投影系数向量S（t），由压缩采样向量Y（t）精确地重构满阵时的阵元接收信号向量X（t）。因此，在压缩采样中，采样矩阵Φ的设计非常重要。根据阵列天线的结构特点，本文设计了2种满足条件且易于系统实现的采样矩阵：

式中，Φ1、Φ2分别对应稀布阵与随机子阵结构。

将式（4）改写成多次快拍的形式得：

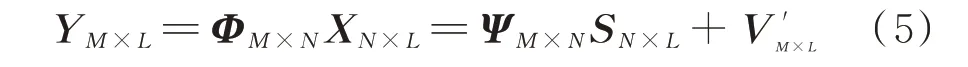
在得到压缩采样信号YM×L后，可以通优化过求解式（6）的问题来恢复：

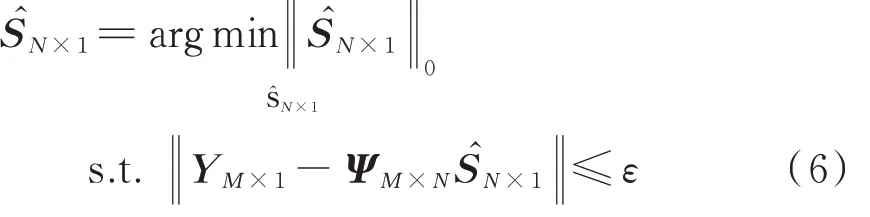
2 改进算法

第1节的讨论都是基于目标在网格上的前提，当目标不在网格上时，重构的输出信号误差将会明显增大。通过增大参数P，减小网格大小可以改善输出误差。但是增大参数P会使计算量急剧上升。根据空间目标在一定时间内角度变换较小这一特点，本文提出了基于多快拍的自适应栅格调整的优化算法。该算法不但提高了恢复精度，而且大大减少了恢复信号所需的计算量。首先将所有得到的采样信号按快拍进行 分 段YM×L=[Y0M×l，Y1M×l，…，YmM×l]，其 中L=l×m。改进后的算法框图如图1所示。

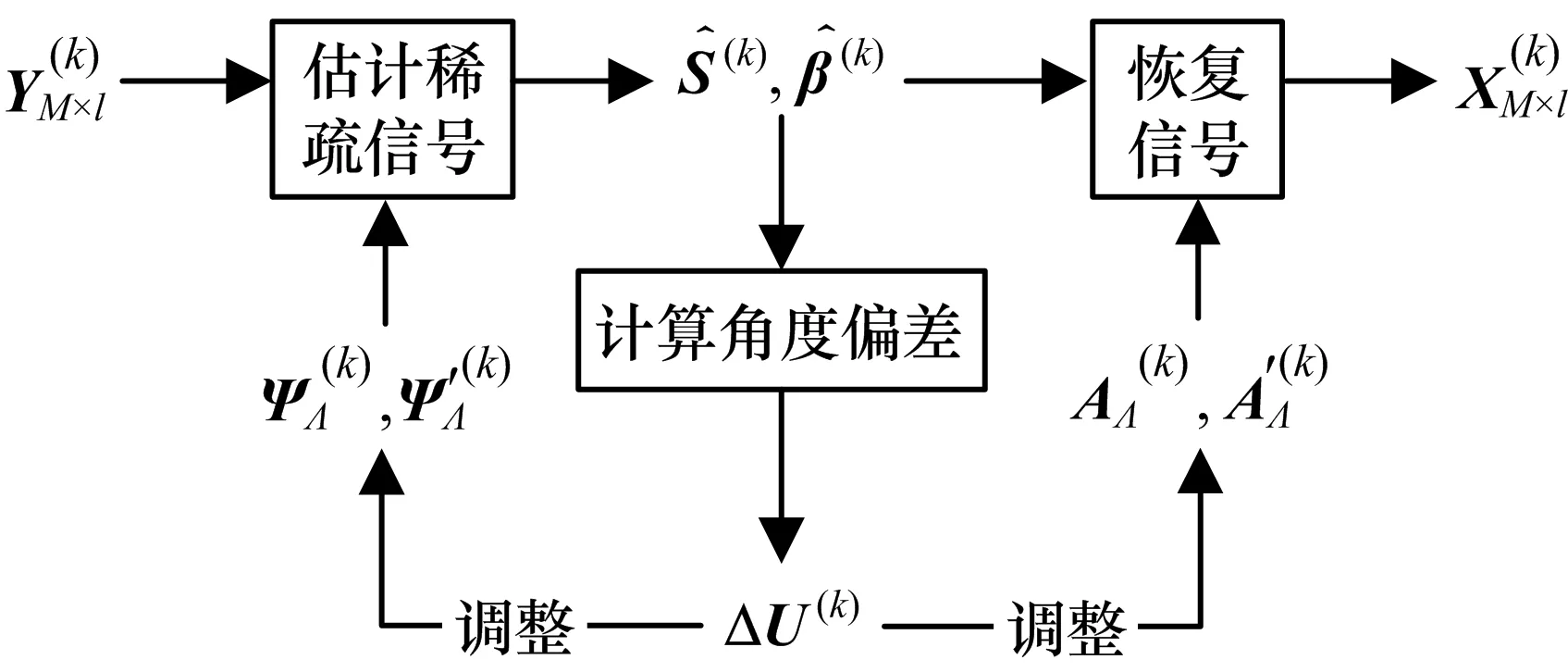
图1 算法框图

多快拍的自适应栅格调整优化算法流程为：

①初始余量r0=Y0M×l，内循环迭代 次数n=1，索引值集合Λ=Ф，J=Ф；

②计算相关系数cM×1=(u1+u2+…+ul)/l，其中ui为矩阵uM×l=|ΨHr|的第i列，查找c中最大值，并将对应的索引值存入J中；

③删除已选中原子，更新支撑集ΨΛ、Ψ’Λ，其中Λ=Λ∪J；

由图1可以看出，该算法根据估计的稀疏信号计算实际角度与预设栅格角度的偏差来调整栅格（支撑集ΨΛ，Ψ′Λ，ΑΛ，Α′Λ），随着调整的次数增多，角度偏差会越来越小，恢复精度也会越来越高。当角度偏差足够小时，可以减少支撑集的更新频率，从而减少支撑集更新之后，在步骤3）中矩阵求逆引入的巨大计算量。改进算法在初始化时，采用多块拍的J-OMP算法，当得到相应支撑集之后，采用逐步调整的方法，逐渐调整支撑集后，经过几次调整之后，角度偏差会很小，支撑集的更新频率也可以降低。该方法减少了重复的原子选择过程。

3 仿真结果分析

3.1 波束性能分析

假设有2个来自不同角度（5°，35°）的空域信号，其中一个是期望信号S（t）（5°），信噪比SNR=10 dB，另外一个为干扰信号I（t）（35°），干噪比INR=40 dB。考虑有一个满阵40阵元的线阵，阵元间距λ/2，随机抽取15个阵元作为稀布阵阵元。对稀布阵数据、满阵（40阵元）接收数据、J-OMP方法恢复数据以及本文方法恢复数据的波束形成性能进行了仿真比较。

图2为几种方法的方向图及零陷：图（a）为波束方向图比较图，图（b）为零陷比较图。由图2可知，稀布阵方法旁瓣较高，且零陷偏移；J-OMP方法和本文方法的方向图旁瓣与满阵相当，且零陷也较深；本文方法得到的零陷更深，更接近于满阵。

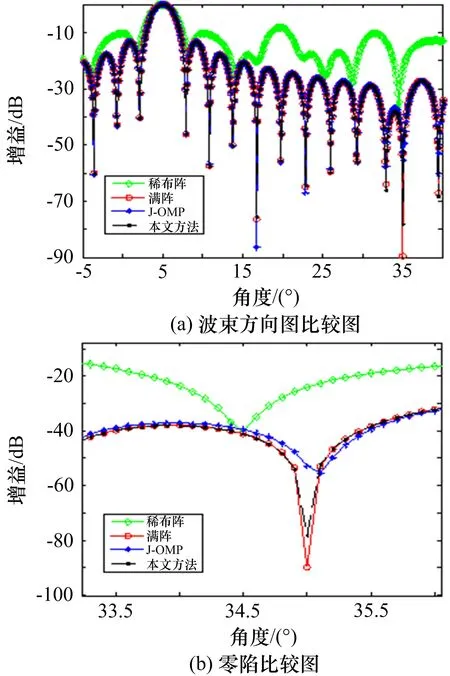
图2 几种方法的方向图及零陷

3.2 不同情况算法性能比较

下面进行目标不在网格上时，OMP方法、J-OMP方法和本文方法的仿真结果比较。仿真时，均采用一个期望信号S（t）和一个干扰信号I（t），期望和干扰的方向都偏离预设栅格，设INR=40 dB，均做100次蒙特卡洛仿真。

图3为SNR=10 dB，INR=40 dB，100个快拍处理的结果比较。可以看出，J-OMP优于OMP方法，经过调整之后本文方法结果明显优于J-OMP方法，接近栅格上的结果。图4为调整完成之后不同输入信噪比下的结果比较，可以看出，本文方法优于J-OMP，较好地解决了不在栅格上的问题。

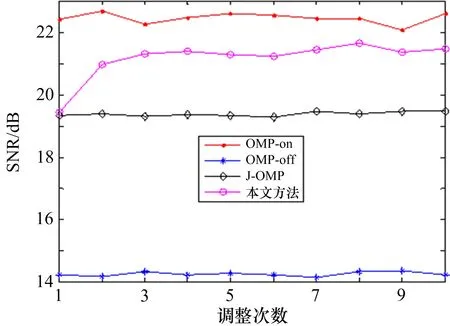
图3 调整之后输出信干噪比（l=100，SNR=10 dB，INR=40 dB）

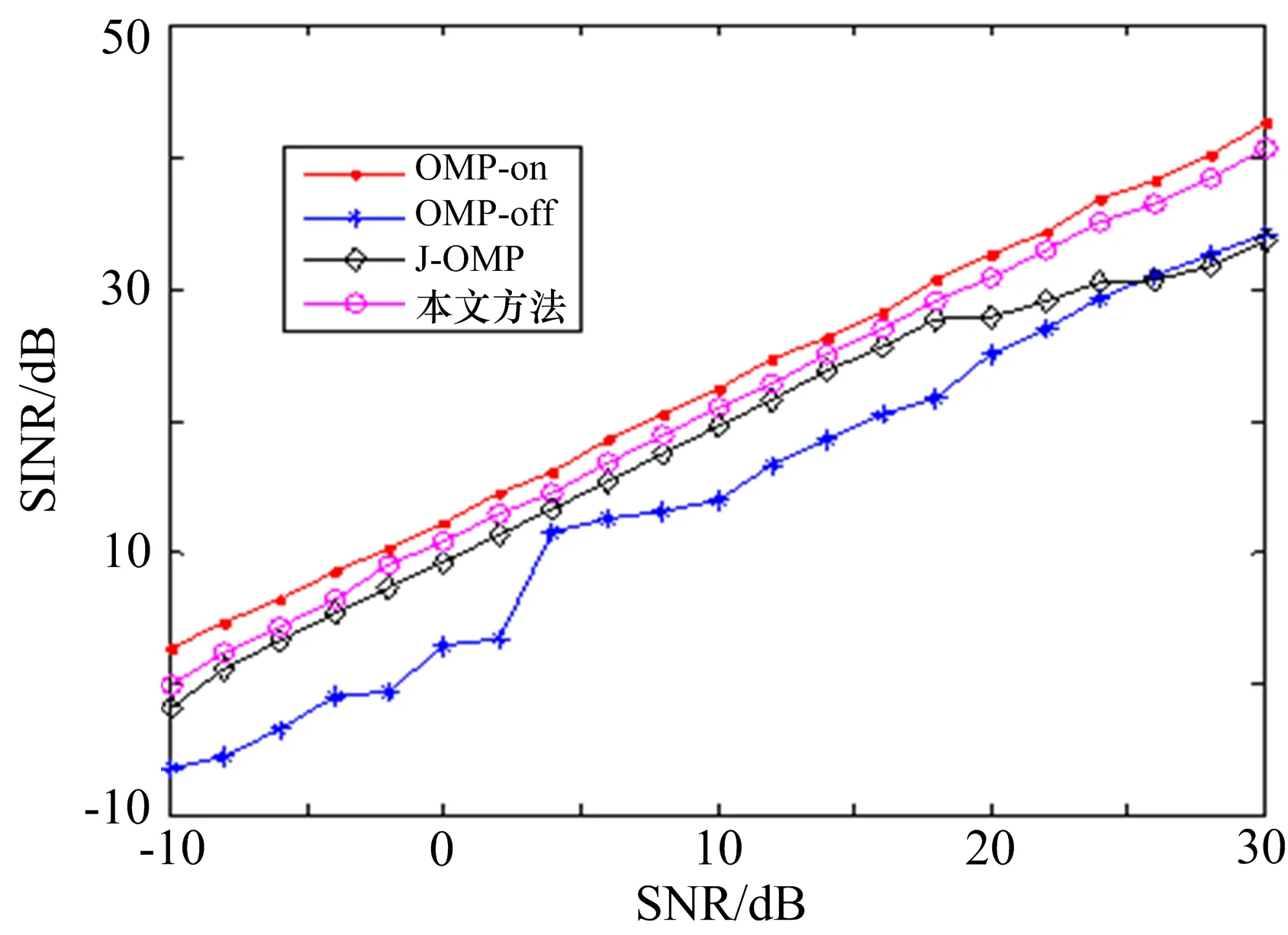
图4 不同输入信噪比下的性能比较（l=100，INR=40 dB）

基于多快拍的信号恢复不仅可以减少计算量，更重要的是，在小信号的情况下，多快拍的处理有助于减小恢复误差，图5为不同快拍处理结果的比较。可以看出，快拍越多，信号恢复越精确，特别是小信号情况下，快拍较少时，信号不能很好地恢复。

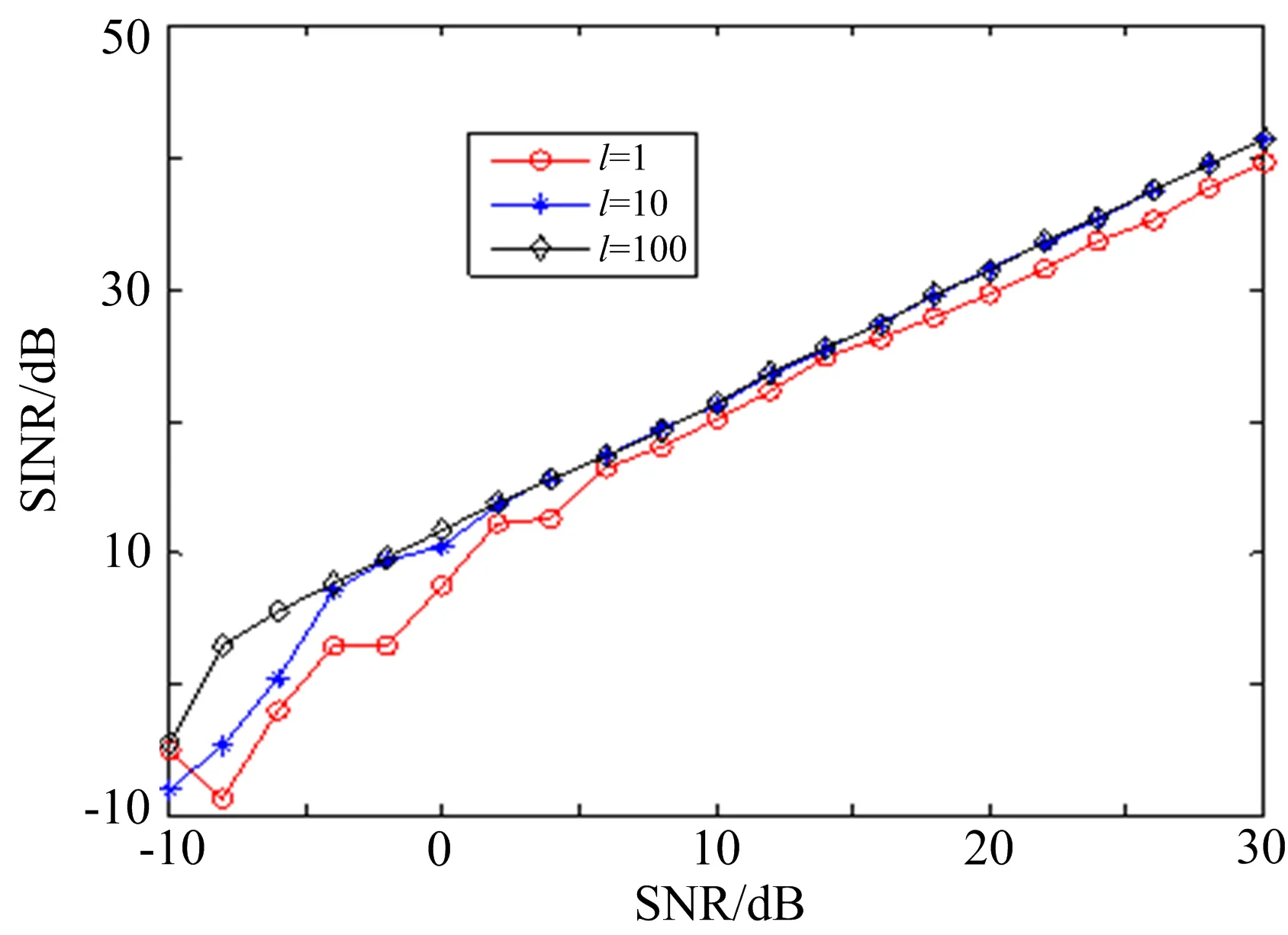
图5 不同快拍下的性能比较（INR=40 dB）

随着栅格的自动调整，目标更接近于栅格，一阶泰勒展开误差更小，所以本文方法恢复效果优于J-OMP方法。图6为不同口径下结果的比较，对于大口径的阵列，本文方法相比于J-OMP方法性能提升较小，但是在小口径阵列下提升较大，可见该方法更适用于小口径的阵列。

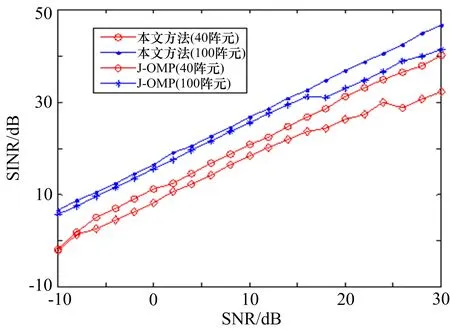
图6 不同口径下性能比较（l=100，INR=40 dB）

本文第1节给出了2种满足条件且易于实现的采样矩阵Φ1、Φ2，图7为2种采样矩阵下的结果比较（均为15个射频通道），可以看出，子阵结构的输出信干噪比优于稀布阵结果。这是因为采用子阵结构时，最后信号能量为40个阵元的叠加，而稀布阵的能量是15个阵元能量的叠加，所以，子阵结构得到的能量大于稀布阵结果。

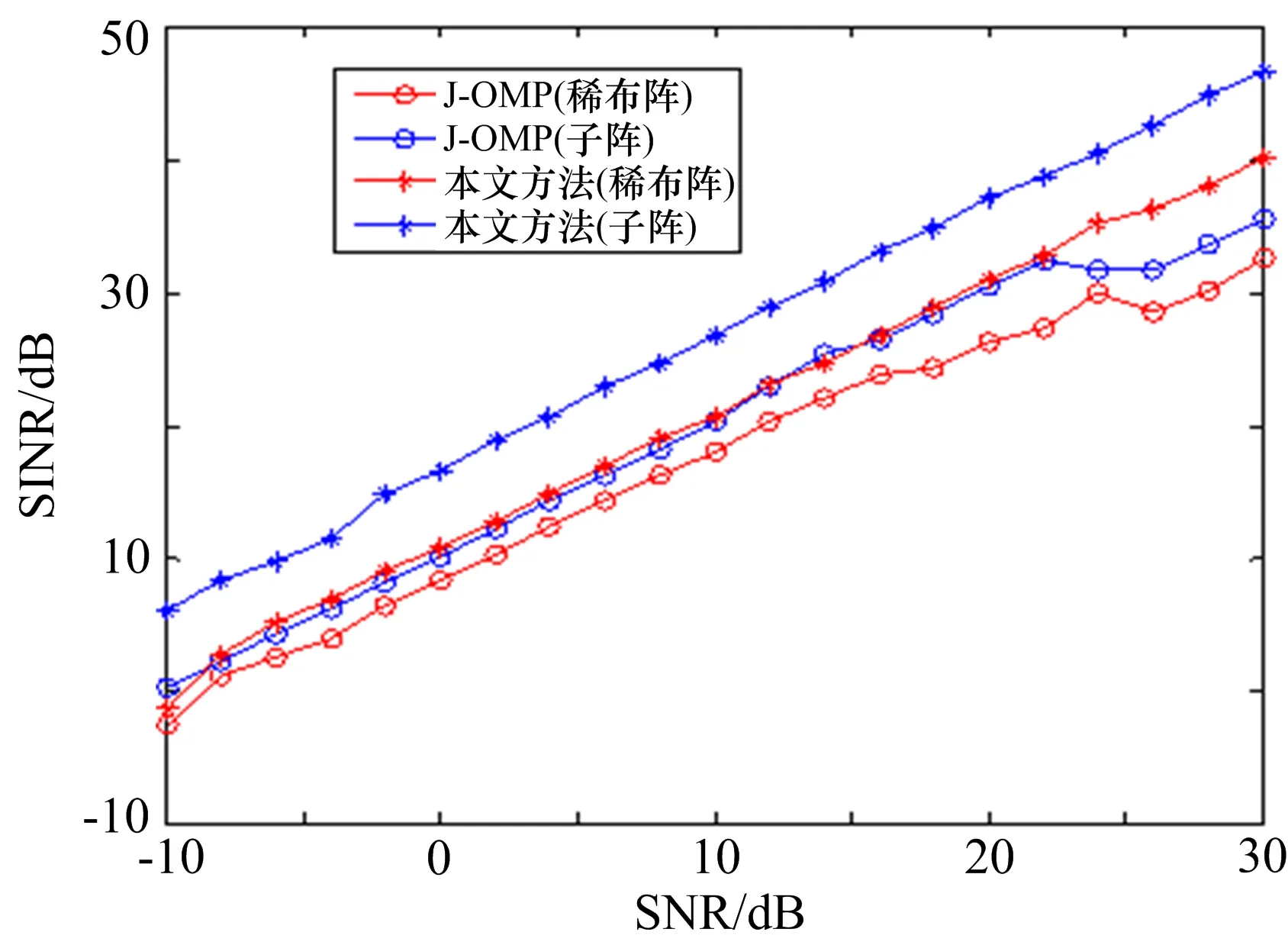
图7 稀布阵与随机子阵性能比较（INR=40 dB）

4 结束语

本文提出的改进的基于多快拍的自适应栅格调整的优化算法，不但在恢复效果上优于J-OMP方法，而且在计算量上也显著减少。该方法可以在不影响波束性能的前提下大大减少射频通道数，从而降低雷达的成本。该方法利用回波信号在空域的稀疏性且变化较慢这一特点，利用栅格的自适应调整提高恢复精度，减少计算量。通过仿真可以看出，该方法与J-OMP方法相比，不仅适用于大阵列还适用于小阵列，多快拍处理性能优于单快拍处理性能，随机子阵结构性能优于稀布阵。■