基于改进Spectrum的肠道菌群聚类算法研究

任玉艳, 熊 馨, 贺建峰*

（1. 浙江长征职业技术学院护理与健康学院, 杭州 310012； 2. 昆明理工大学信息工程与自动化学院, 昆明 650500）

糖尿病（diabetes mellitus, DM）是一种因胰岛素分泌缺陷或胰岛素作用障碍所导致的慢性代谢性疾病[1-2]。在DM中2型糖尿病（type 2 diabetes mellitus, T2DM）所占比率超过90%, 其中胃肠道病变是严重影响DM患者的主要并发症之一[3-5]。研究表明[6-7], 肠道菌群失调与T2DM的发生有着一定的联系, 但详细作用机制并不十分清楚。目前对肠道菌群研究中较多的是对菌群的群落组成和多样性的分析, 用于研究微生物生态学的基本问题之一：有多少类群或者分类操作单元（operational taxonomic units, OTUs）存在？通常采用多变量统计或者模式识别方法, 识别菌群数据中的不同结构模式, 如主成分分析（principal component analysis, PCA）[8-10]、主坐标分析（principal coordinate analysis, PCoA）[11-13]、围绕中心点划分聚类[14-15]等。这些方法存在一些固有问题, 一方面高多样性的微生物组学数据往往数据集稀疏, 另一方面大多数分类单元仅出现在少数低丰度的样品中。此外, 微生物基因样本的小样本的固有噪声比大样本大。

在肠道微生物菌群结构的比较研究中, 传统的聚类方法如K-means[16]、层次聚类[17-18]、分区聚类、基于网格的聚类[19-20]等作为非监督学习算法被广泛使用。不同的是, 谱聚类更适用于具有不同的密度、随机的复杂形状和不稳定的大小的数据集, 并且计算量偏小, 展现出更高的性能。谱聚类算法基本可以分为二路谱聚类算法和多路谱聚类算法这两种类型, 前者主要是以二路谱聚类算法（PF算法）为代表且采用图的二路划分准则, 后者主要是以多路谱聚类算法（NJW算法）为代表且采用图的多路划分准则[21]。

谱聚类算法的相似度矩阵需要高斯核函数构造, 其参数需人为选定, 且特征向量并没有统一的标准。Zelnik等[22]提出self-tuning谱聚类算法, 针对每个样本定义局部尺度参数, 并将自适应的局部尺度参数定义为样本i与其第p个近邻的距离。但是此方法依旧没有解决高斯核函数参数受经验值影响的问题。王玲等[23]将相似性度量变为基于密度敏感的相似性度量, 能在较大尺度范围内得到较好的聚类结果。Xie等[24]提出了基于样本局部标准差的谱聚类算法, 自适应的局部尺度参数a被定义为样本与其第p个近邻距离的标准差, 但参数p仍依赖经验值[24]。如何解决自适应选取参数的问题以构造尽可能反映真实样本内部的相似性矩阵, 以及谱聚类算法的聚类结果不稳定等问题仍需要在该算法基础上进行持续性研究。

本文以T2DM肠道菌群数据集为例, 提出成对比率几何平均值（geometric mean of pairwise ratios, GMPR）结合改进的Spectrum算法。首先, 针对菌群数据稀疏问题, 采用GMPR进行归一化；然后, 针对数据存在噪声的问题, 因Spectrum算法对单类人群识别效果不佳, 提出改进的Spectrum算法, 通过构造加权的相似性矩阵可计算每个样本所对应的不同特征值大小在该样本中所占据的权重, 再将拉普拉斯矩阵替换为Hessian矩阵, 避免传统谱聚类的灵敏度问题；最后, 结合ISODATA算法找到最佳聚类。使用本文所采用的聚类方法进行OTUs聚类后, 可以找出患病人群与健康人的菌群结构差异, 这些核心菌群在人体菌群中起到关键性的作用。探讨肠道菌群与T2DM、2型糖尿病合并腹泻的关系, 可能成为治疗、预防这些疾病的一个突破口；使用信息处理手段识别T2DM患者肠道菌群数据的结构变化, 为疾病的预防和诊疗提供了一种新的手段。

1 材料与方法

1.1 试验数据集

本文所采用的T2DM数据集均来源于云南省第一人民医院消化科, 经云南省第一人民医院伦理委员会批准, 所有受试者均签署知情同意书。数据集包含140例样本, 其中包括T2DM（简称为D）患者74例, 2型糖尿病合并胃肠自主神经病变（简称为P）患者27例, 健康人（简称为N）39例。试验中使用的数据为绝对丰度数据。

1.2 GMPR

GMPR是一种专门用于解决数据零膨胀问题的归一化方法[25], 能够解决数据特征中包含大量零以及测序深度不一的问题。

GMPR用来计算给定样本的尺寸因子Si, 可以对给定样本的（相对）库大小进行估计, 其公式如下：

首先是计算rij,

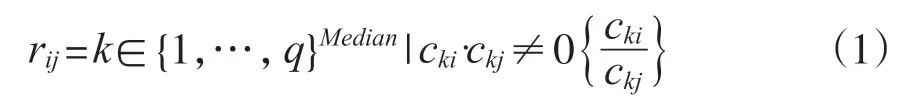
其中k代表OTUs数目,rij代表样本i和样本j之间非零计数的中值计数比,ckj表示为第i个（i=1, …,n）样本中第k个（k=1, …,q）OTUs的计数。

再计算给定样本i的尺寸因子Si,

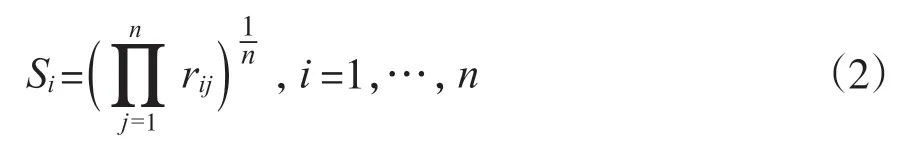
简单来说, GMPR是把OTUs计数表中的样本两两间进行成对比较, 将成对比较结果合并以获得最终估计值。

1.3 Spectrum算法

Spectrum算法[26]把数据分析问题看作是图的最优分割问题, 它在构建相似矩阵时采用自调整密度感知内核, 进一步增强最近邻点之间的相似性, 同时降低噪声, 并且Spectrum算法可以实现寻找分析涉及特征向量分布的最佳聚类数（K）, 自动找到高斯和非高斯结构的K[26]。

对于输入的OTUs利用Spectrum算法中的自适应密度感知内核, 经计算得到相似性矩阵A*。从A*开始, Spectrum算法使用Ng谱聚类方法, 同时使用特征值启发式方法来估计聚类的数量, 最后利用高斯混合建模（gaussian mixture model, GMM）/K-means对特征向量矩阵聚类, 对OTUs所代表的特征簇进行划分。

1.4 改进Spectrum算法流程

改进的Spectrum算法是将输入数据通过加权的自适应密度感知内核计算相似性矩阵A*。从A*开始, 该算法使用Ng谱聚类方法, 同时使用特征值启发式方法来估计聚类的数量, 最后利用ISODATA来聚类最终的特征向量矩阵, 对OTUs所代表的特征簇进行划分。

1）改进Spectrum算法首先是使用加权的自适应密度感知内核计算相似性矩阵, 矩阵A*∈Rn×n。加权的自适应密度感知内核为：

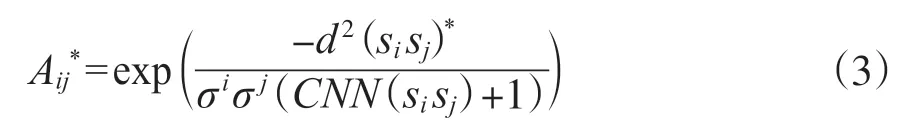
其中,d（sisj）*表示Si和Sj（即不同OTUs）之间的欧几里得距离,σi和σj是局部缩放参数,CNN（sisj）表示点Si和Sj周围球体半径邻域的连接区域中的点数。

2）计算对角矩阵D,D中（i,i）元素代表总和A*的第i行, 利用D构建Hession矩阵H：

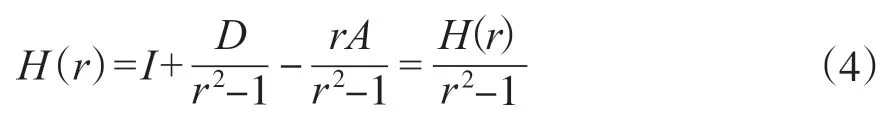
其中,H（r）=（r2-1）I-rA+D。A代表相似度矩阵,D代表对角矩阵,I代表单位矩阵。在稳定点, 根据光谱半径的值计算正则化参数ρ（B）代表非回溯矩阵B的谱半径。首先计算谱半径ρ（B）=mean（d2）/mean（d）-1[28],d代表度。

3）对H进行特征分解并求解特征向量X1,X2, …,Xn+1和特征值λ1,λ2, …,λn+1。

4）判断特征值的差值, 从第二个特征值开始,n=2, 并选择最佳k, 其中特征差值最大用k*表示：

5）得到x1,x2, …,xk*,H的k*个最大特征向量, 然后形成矩阵X（每个特征向量按列排列）组成k*维空间的n个向量, 即X=[x1,x2, …,xk*] ∈RN～+k*。

6）将X矩阵按行进行归一化得到矩阵Y：

7）Y的每一行被视为一个样本Si, 最后所有样本利用ISODATA被聚类成K*类, 得到的类别标签即原始数据点的类别标签。

1.5 加权相似度矩阵

本文提出基于特征贡献度加权自适应密度感知核函数, 得到的样本特征的相似度更加准确。

特征权重计算的主要公式如下：

原始数据集S={si｜si∈S,i=1, 2, …,n}, 其中每个样本包含m个特征（即m个OTUs）, 则可表示为Si={si1,si2, …,sim}。

特征差异度p计算公式如下：

其中,pm代表每一列特征的变化情况。

特征差异度[29]通常采用方差来表示特征存在的整体误差情况, 容易出现偏差。因此, 本文使用了另一种计算p的方式, 公式如下：

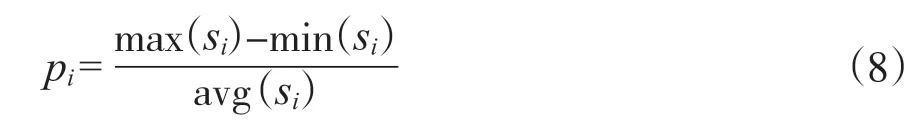
其中,Si表示某一列的数据, max（si）代表该列的最大值, min（sj）代表该列最小值, avg（si）代表该列的平均值。p值越大代表该特征的差异度越大。

本文计算特征差异度比值的最大值maxr, 目的是通过maxr了解是否存在最大最小特征差异度。

特征差异度比值的最大值公式如下：

其中,Pi、Pj分别表示第i列与第j列的特征差异度。

特征权值w的计算,w={w1,w2, ...,wm},w表示m个特征在计算欧几里得距离时的m个特征贡献度。本文利用Softmax函数计算特征权重, 其公式如下：

其中,Pi为每个特征差异度。Pi越小, 代表该特征贡献度越小。

使用Softmax函数不仅可以突出最大特征贡献度, 还可以遏制低于最大值的其余分量[30]。但Softmax函数会在某些情况下特征权重失衡, 此时采用Sigmoid 函数, 函数鲁棒性强, 失衡的特征权重可被映射到有限的区间, 平衡特征权重失衡现象, 因此原本的wi计算公式也发生更改, 即：

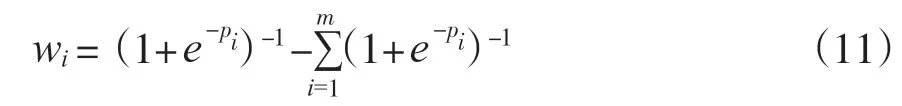
wi代表每一个OTUs所对应的权重大小, 对每个特征赋予权重后, 传统的欧几里得距离就可更改为加权的欧几里得距离, 其公式如下：

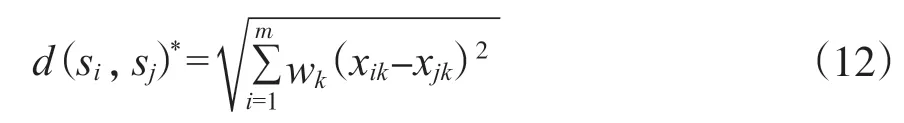
随即特征Si和特征Sj的自适应密度感知内核可调整为：

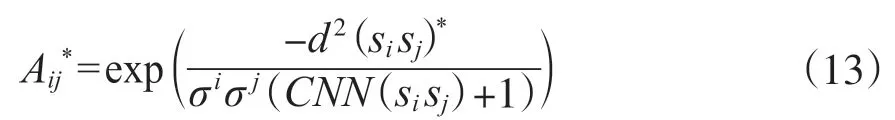
1.6 Hession矩阵

本文采用Hessian矩阵代替原始谱聚类的拉普拉斯矩阵, 可以避免传统谱聚类的灵敏度问题[31-32]。

1.7 ISODATA算法

ISODATA算法可以依据每个簇的不同现实情况不断改变预期的聚类中心数目K, 主要是通过分裂和合并这两种方式来实现。分裂可以使得K增加, 合并可以使得K减少。ISODATA中K的变动区间是[K/2, 2K] 。该算法需要额外指定一些参数, 导致一个合理值的获得很难被准确指定。本文中通过设置合理的参数, 可以得到一个较好的试验结果。

ISODATA算法的基本流程如下：

1）随机选取K个初始聚类中心, 它可以不等于所要求的聚类中心的数目, 其初始位置可以从样本中任意选取；

2）计算各个样本xi到K个聚类中心的距离d,d最短时就把此时对应的样本划分到聚类中心所在的簇中；

3）判断找出的每个簇中的对象数目是否低于Nmin, 即每个簇所规定的最小样本数目。一旦低于Nmin则该簇就会被丢弃, 此时K=K-1, 并把该簇中的样本再一次划分到K-1类中距离最短的那一簇中；

4）对每个簇ci的聚类中心进行新一轮的计算, 即

5）一旦K≤K/2时, 代表簇数目太少, 进行分裂操作；

6）一旦K≥2K时, 代表簇数目太多, 进行合并操作；

7）当最大迭代次数达到最大时就停止操作, 否则返回流程2）重新运行。

使用ISODATA算法进行聚类时可以根据各个簇所包含样本的实际数量对聚类中心数目进行调整。比较方差后发现, 某个簇中样本离散程度大时就对其进行分裂；比较过聚类中心的距离时, 一旦发现某两个簇距离较短则进行合并。

2 结果与分析

2.1 聚类数目

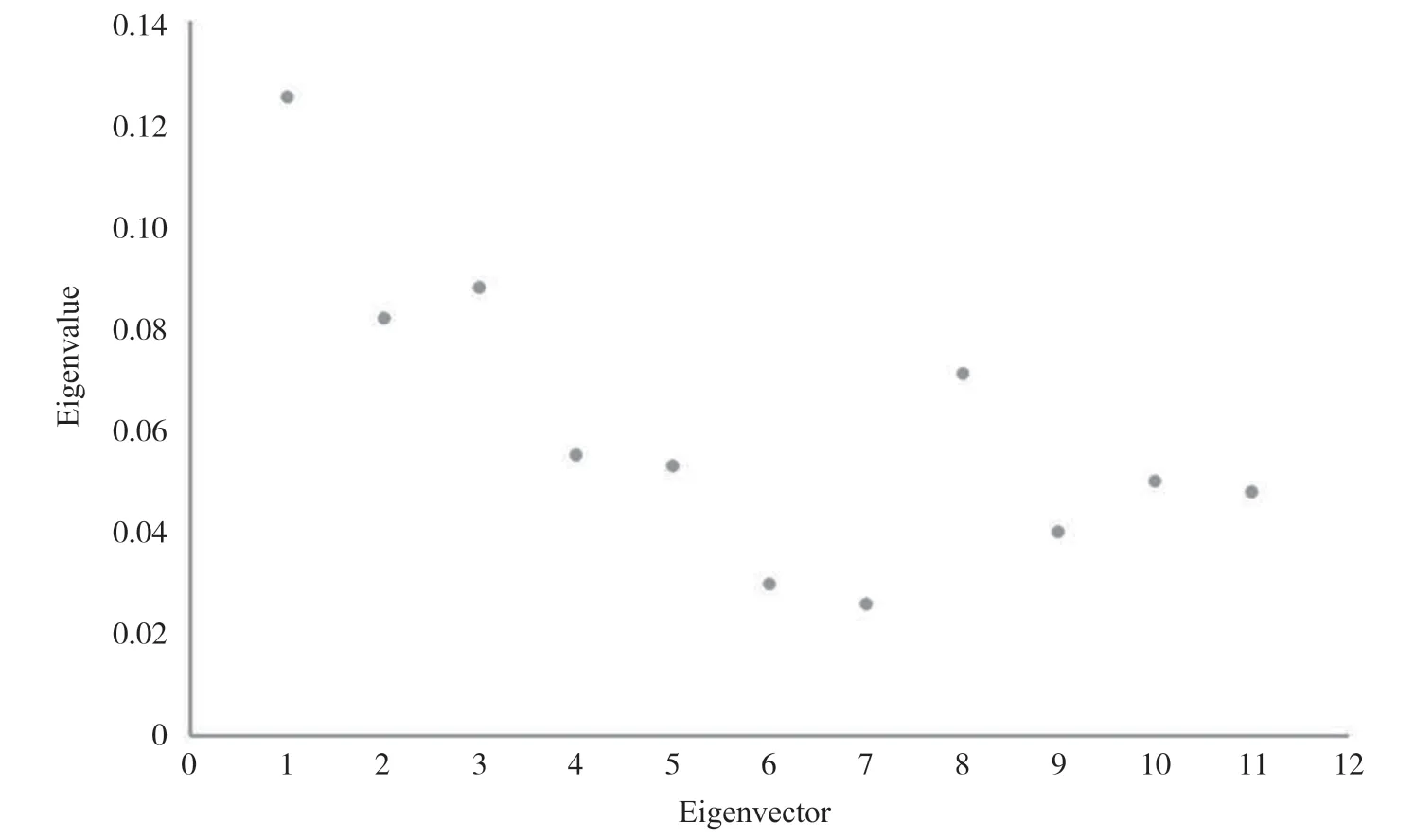
为了验证算法聚类性能的好坏, 对T2DM数据集不同类型人群分别进行分析, 将特征值的差值（相邻的两个特征向量所对应的特征值进行做差, 即特征值的差值）最大时所对应的k作为最优的聚类数目。如图1所示, 以T2DM中的D类人群为例, 在特征向量为7、8时, 二者之间的特征值差值大约为0.4, 达到一个特征值的差值最大, T2DM患者所对应的最佳聚类数目为8, 其余类别人群聚类情况与图1类似。

为了验证改进后Spectrum算法聚类性能, 对T2DM数据集不同类型人群分别进行分析, 得到D、P、N类人群的最佳聚类数目如表1所示。

表1 T2DM数据集在不同类型人群下的聚类数目Tab. 1 Number of clusters of T2DM dataset under different types of populations

2.2 聚类评价指标

本文通过比较标准化互信息（normalized mutual information, NMI）、戴维森堡丁指数（Davies-Boulding index, DBI）、Calinski-Harabasz指标（CH）、兰德指数（Rand index, RI）及调整兰德指数（adjusted Rand index, ARI）来评估算法的性能。这些指标定义及公式如下所述。

2.2.1 NMI

NMI是确定聚类质量的常用方法[33]。NMI值越大, 意味着性能越好。设两个随机变量x,y的联合分布为p（x,y）, 边缘分布分别为p（x）,p（y）。互信息I（X,Y）是联合分布p（x,y）与乘积分布p（x）p（y）的相对熵, 它可以看成是一个随机变量由于已知另一个随机变量而减少的不肯定性, 公式为：

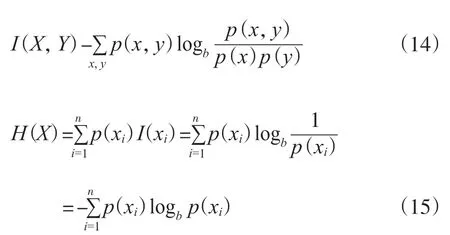
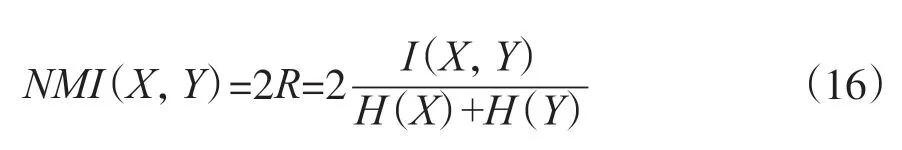
2.2.2 DBI

DBI越小, 类内距离越小, 聚类效果越差[34]。

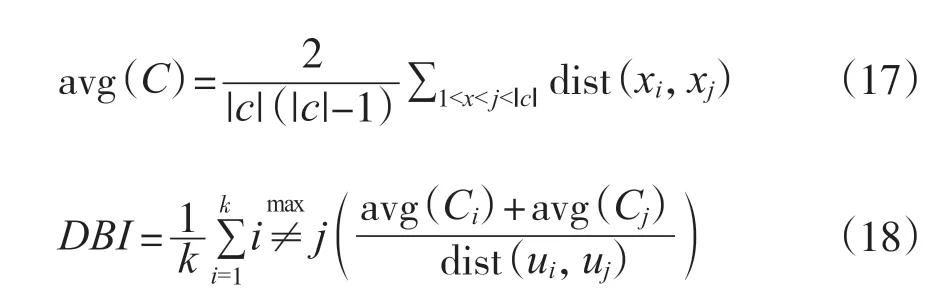
其中avg（C）含义为簇类C的平均距离, ｜c｜表示簇类C的个数, dist（xi,xj）是计算两个样本xi,xj之间的距离, 其中ui,uj分别为簇类Ci,Cj的中心。

2.2.3 CH

CH指标主要计算簇间距离与簇内距离的比值[35]。CH（K）值越大, 聚类效果越好。公式如下：

2.2.4 RI

RI[36]将聚类看成是一系列的决策过程, 当且仅当两个OTUs特征相似时, 将它们归入同一簇中。RI需要给定实际类别信息C, 假设K是聚类结果,a表示在C与K中都是同类别的元素对数,b表示在C与K中都不是同类别元素的个数, 则RI定义如下：

其中, C2nsamples表示数据集中可以组成的总元素对数。RI取值范围为[0, 1] , 值越大表示聚类效果准确性越高, 每个类内的纯度越高。

2.2.5 ARI

为了实现“在聚类结果随机产生的情况下, 指标应该接近零”, 在RI无法保证随机划分的聚类结果的RI值接近零的情况下, 利用了具有更高区分度的ARI[36]：

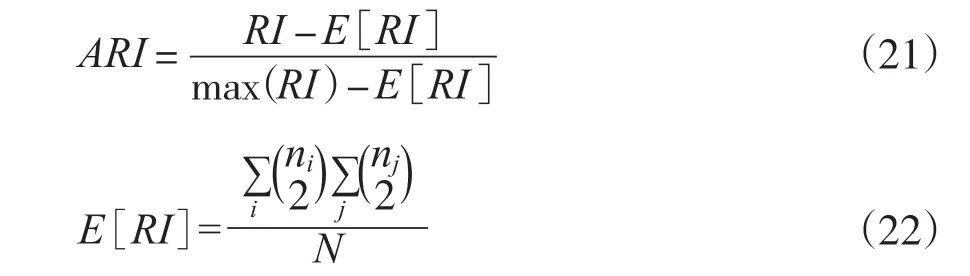
ARI取值范围为[-1, 1] , 值越大意味着聚类结果与真实情况越吻合。

2.3 评价指标结果

本文所使用的所有聚类算法, 同样也对D、P、N三类人群的OTUs数据集的各个特征进行聚类, 改进Spectrum与Spectrum相比, 改进Spectrum在D、P、N中NMI、CH、RI、聚类数目均优于Spectrum, 除了P中ARI低于Spectrum, 以及DBI在各类人群中均不如未改进前的算法。GMPR+改进Spectrum与GMPR+Spectrum相比, GMPR+改进Spectrum在D中除了DBI以外其余各项指标均优于GMPR+Spectrum。在P、N中, GMPR+改进Spectrum中的NMI、CH、RI均好于GMPR+Spectrum, 而P中ARI低于GMPR+Spectrum, 而GMPR+改进Spectrum中全部人群中的DBI均不如GMPR+Spectrum。但综合来看, 无论是GMPR+改进Spectrum还是改进后的Spectrum算法, 即使出现个别评价指标不如改进前的Spectrum, 总体上来说还是达到一个较好的水平, 证明了改进后算法的有效性。

2.4 改进Spectrum识别出的肠道菌群（属水平）

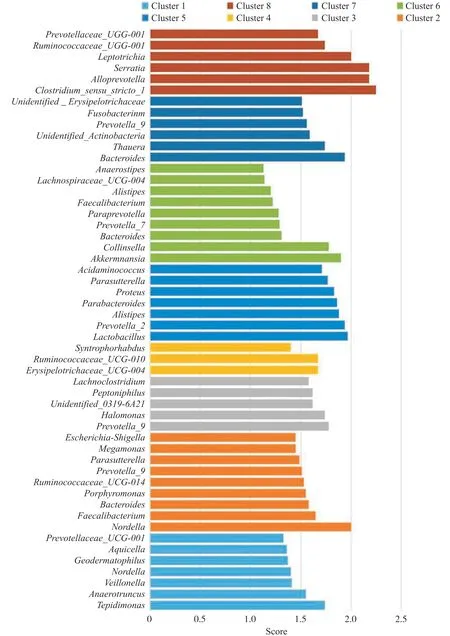
利用GMRP+改进Spectrum算法对每一类人群进行聚类, 得到T2DM患者、2型糖尿病合并腹泻患者以及健康人依次被聚为8、10、7类, 根据算法中的score值找出每类人群中的关键OTUs。score值代表某个OTUs的方差占全部方差的比重, 实际也就是某个特征值占全部特征值总和的比重。score值越大, 贡献率越大, 说明该OTUs所包含的原始变量的信息越强。因此, 将score值大小作为判断某一个OTU是否是核心菌群的衡量标准。在D组的每一个cluster包含的核心细菌可见图2。横轴代表不同细菌在不同cluster中的score值, 纵轴代表每个cluster中包含的核心细菌。不同颜色代表不同的cluster。D、P、N组的不同cluster的核心OTUs详细信息形式与图2一致。

在T2DM数据集中,Tepidimonas、厌氧棍状菌属（Anaerostipes）、诺卡氏菌属（Nordella）、地嗜皮菌属（Geodermatophilus）、Aquicella、粪杆菌属（Faecalibacterium）、巨单胞菌属（Megamonas）、大肠埃希菌志贺氏菌属（Escherichia-Shigella）、嗜盐单胞菌属（Halomonas）、Syntrophorhabdus、乳酸杆菌属（Lactobacillus）、另枝菌属（Alistipes）、纤毛菌属（Leptotrichia）等细菌是2型糖尿病合并腹泻患者所独有的, 而在健康人核心菌群中未发现这些细菌。

在T2DM数据集中,Reyranella、瘤胃球菌属（R uminococcaceae_UCG-014）、Rubrobacter、氨基酸球菌属（Acidaminococcus）、另枝菌属（Alistipes）、乳酸杆菌属（Lactobacillus）、Akk菌（Akkermansia）等细菌是T2DM患者所独有的, 而在健康人核心菌群中未发现这些细菌。

在T2DM数据集中,Tepidimonas、厌氧棍状菌属（Anaerorhabdus）、韦荣氏球菌属（Veillonella）、Nordella、地嗜皮菌属（Geodermatophilus）、Porphyromonas、普雷沃氏菌属（Prevotellace_UGG_001）、巨单胞菌属（Megamonas）、嗜盐单胞菌属（Halomonas）、沙雷氏菌属（Serratia）、纤毛菌属（Leptotrichia）的这些细菌是2型糖尿病合并腹泻患者所独有的, 而在T2DM患者核心菌群中未发现这些细菌。Reyranella、瘤胃球菌属（Ruminococcaceae_UGG_0 10）、Rubrobacter、Silanimonas、梭菌（Clostridium_sensu_stricto_1）等细菌是T2DM患者所独有的, 而在2型糖尿病合并腹泻患者核心菌群中未发现这些细菌。

菌群对比后发现, D、P、N组经改进后Spectrum方法聚类后, 可以识别出每类人群具有的标志性细菌, 可以区分出健康人、T2DM及2型糖尿病合并腹泻患者在不同OTUs之间的相似性以及存在的菌群结构差异。

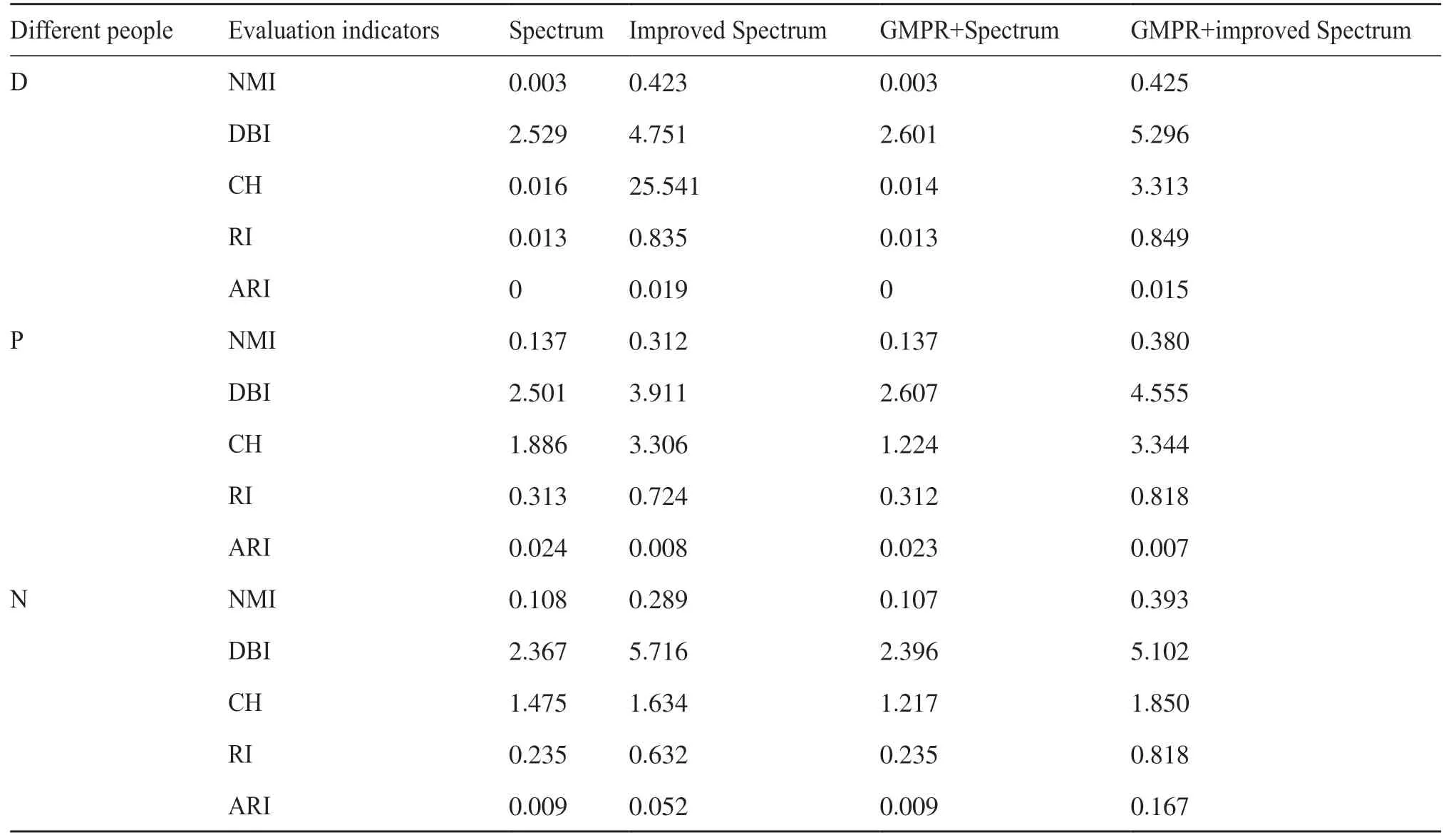
表2 T2DM中不同人群在各个算法中的各项评价指标Tab. 2 Evaluation indicators of different people in T2DM in each algorithm

3 讨论

本文采用改进Spectrum算法对T2DM数据集进行聚类, 由于肠道菌群在测序过程中存在的缺失或者是采样不足, 导致测序数据出现零膨胀问题。因此, 采用GMPR方法对肠道菌群进行归一化, 有效避免肠道菌群数据零膨胀问题。然后, 采用改进Spectrum算法进行肠道菌群结构分析。结果显示, GMPR+改进Spectrum算法与GMPR+Spectrum、Spectrum等算法在不同类型数据上相比时, 在聚类效果、NMI、CH、RI、ARI上表现良好。总的来说, GMPR+改进Spectrum算法在相关性能上更具有优势。

经GMPR+改进Spectrum方法识别出的核心细菌中, 发现乳酸杆菌属只存在于D的核心细菌中。Remely等[37]和Larsen等[38]的研究发现乳酸杆菌属在T2DM中较高。Murri等[39]也发现普雷沃氏菌属在T2DM中较高, 而在本文中目前只发现了乳酸杆菌属, 普雷沃氏菌属或许可以作为一种区分T2DM与正常人的关键细菌, 具体的免疫调节作用机制还有待后续研究。

布劳特氏菌属的变化对T2DM 患者的影响, 在Egshatyan等[40]的研究中得到了证实。该研究表明, 健康人、糖尿病前期与T2DM患者在粪便微生物组成上会发生变化, 这些细菌的变化与T2DM严重程度有关, 布劳特氏菌属在不同类型人群中存在差异, 或许该细菌可以作为一种关键细菌针对临床的T2DM患者进行相应的疾病筛查及诊断。

此外, GMPR+Spectrum识别出T2DM患者核心菌群中的嗜冷杆菌、库尔勒海洋杆菌、栖瘤胃解纤维素菌、环丝菌属、金黄杆菌属、厌氧球菌属, 这些细菌同样也是正常人核心菌群中所没有的, 但在目前的研究中, 还未发现以上这些细菌与T2DM以及2型糖尿病合并腹泻患者的相关作用机制。

不同类型人群识别出的肠道细菌存在差异, 相关肠道细菌的研究机制目前尚不清楚。细菌失衡是导致疾病的发生发展的主要原因, 也是疾病状态的一种现实反映。在现今医疗技术中, 临床筛查T2DM以及2型糖尿病合并腹泻患者仍然面临各种各样的困难, 希望本研究发现的细菌可以为临床患者的筛查和诊断提供一些参考。同时, 本试验的局限性在于样本存在一些个体差异以及试验数据量过少, 且肠道菌群易受到其他因素的影响, 需要经常开展多种族、长期的大型研究。