基于ARIMA-SVM模型的短时交通流量预测研究
陈 昆,曲大义,贾彦峰,王 韬,洪家乐
(青岛理工大学 机械与汽车工程学院,青岛 266525)
随着社会经济的高速发展,生活水平不断提高,汽车拥有量显著增加,截止到2019年底,国内的汽车数量约为2.615亿辆,相比于2018年末增加了2122万辆,其中私家车数量约为2.235亿辆,增加了1905万辆[1]。拥堵已经成为了城市交通状况的常态,为了缓解这一问题,有的城市选择在原有的道路条件下进行扩建,但其成本过高。从长远来看应当利用智能交通系统对交通拥堵进行有效地疏通,其中交通流预测起着至关重要的作用[2-3],能实时地为出行者提供有效的信息,有助于交通控制和交通诱导,提高通行效率[4]。当前在短时交通流量预测方面提出的方法包括:基于传统统计分析方法的模型和基于现代化智能信息处理的模型。第一种包括:回归分析预测[5]、时间序列的自回归统计以及概率预测[6]等方法;第二种方法为非参数模型,其对复杂数据有较强的处理能力,能够较好地提取交通流中的非线性特征[7],如SVM模型(Support Vector Machines)。姚亚夫等[8]利用ARIMA模型(Auto-regressive Integrated Moving Average model)对交通流量进行预测,并证明了该方法的合理性。陈军等[9]用SVM模型和BP模型(Back Propagation)分别对交通流量进行了预测,其结果表明了SVM模型在预测城市交通流量方面的优越性。蒋晓峰等[10]通过遗传算法优化了SVM模型中的超参数,得到了良好的预测结果。
但上述的方法尚未考虑交通流的复杂性。从交通流的特征来看,在同一位置的交通流参数具有长期趋势性,且通常认为预测的交通流量与历史的交通流量数据存在一定的线性关系,但又因其交通的随机波动性,导致交通流中亦存在非线性关系。ARIMA模型能够准确处理交通流量中的线性特征,而SVM模型能够捕捉其中的非线性特征,且具有鲁棒性的优点,因此利用上述模型的组合形式能更好地预测交通流量并提高其预测准确性。本文将ARIMA与SVM组合起来,构建了ARIMA-SVM组合预测模型,并利用文献[11]中西安市区道路的交通流量数据对模型进行仿真分析,且对比了ARIMA-SVM模型与ARIMA和SVM单一模型的预测精度。
1 交通流预测模型
1.1 ARIMA模型
ARIMA模型是在ARMA的基础上将非平稳的时间序列经过差分处理为较为平稳的时间序列进行预测。交通流存在一定的周期性,使得交通流数据成为具有趋势变化的一种时间序列[12],因此对城市道路的短时交通流预测可以利用ARIMA模型。其公式为
(1)
式中:yt,yt-i分别为预测值和历史交通流数据;μ为常数项;γi,θi分别为自相关系数和误差项系数;p,q分别为自回归阶数和移动平均阶数;εt,εt-i分别为模型的误差和时间点i的偏差。
将预处理之后的西安市道路流量数据进行时间序列稳定性检验,通过ADF法检验其是否存在单位根。利用MATLAB数值仿真软件中的ADF test()函数进行检验,当返回值为1时,即表示该交通流数据相对平稳;当返回值为0时,则认为其不平稳。将所得的交通流数据用函数检验得到的返回值为0,之后对数据进行一阶差分处理,即差分次数d=1,重复上述操作,得到的返回值为1,表示序列平稳,即初步认定ARIMA(p,d,q)中得d值为1。
将经过一阶差分后的交通流序列分别通过自相关系数ACF和偏相关系数PACF进行相关性检验,通过观察相关函数图,得到最优的p和q,取95%的置信区间。
通过图1可以看出,在偏相关函数和自相关函数第4阶出现截尾和衰减趋于0的现象,即确定q=4,p=4。
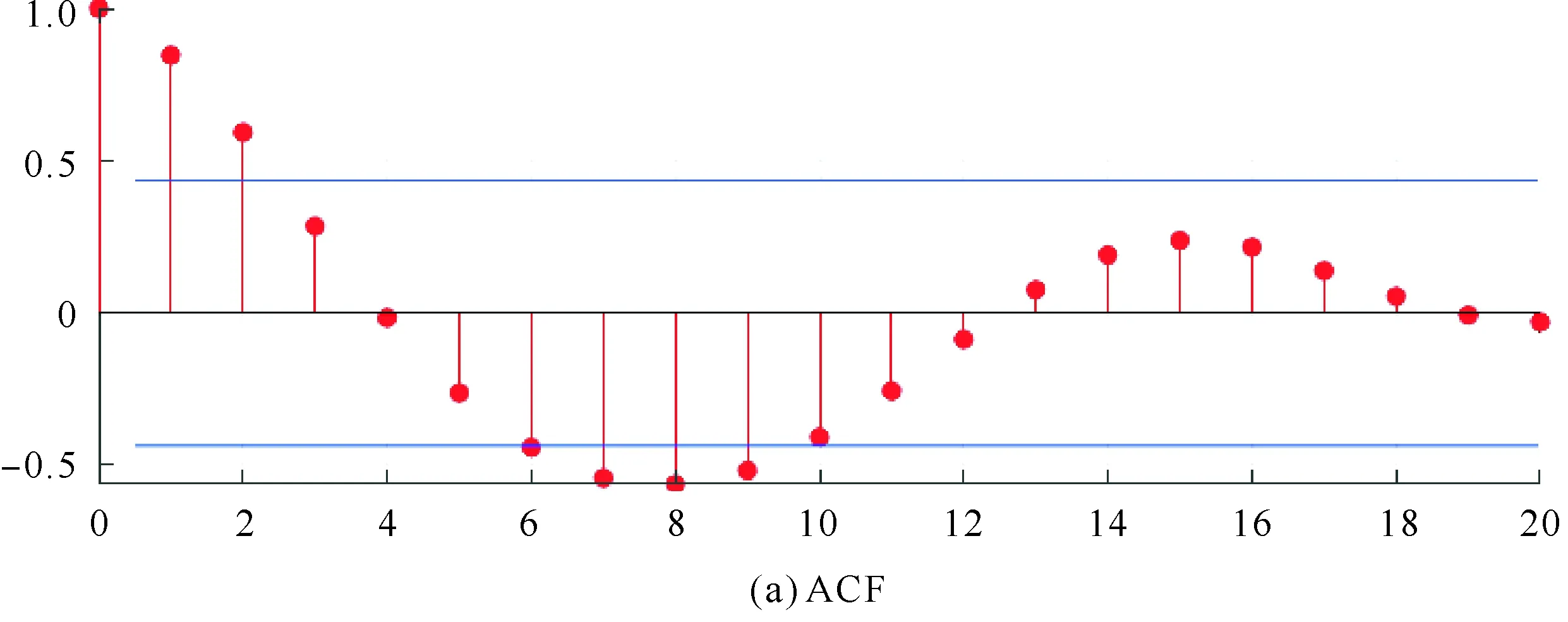
图1 相关函数图
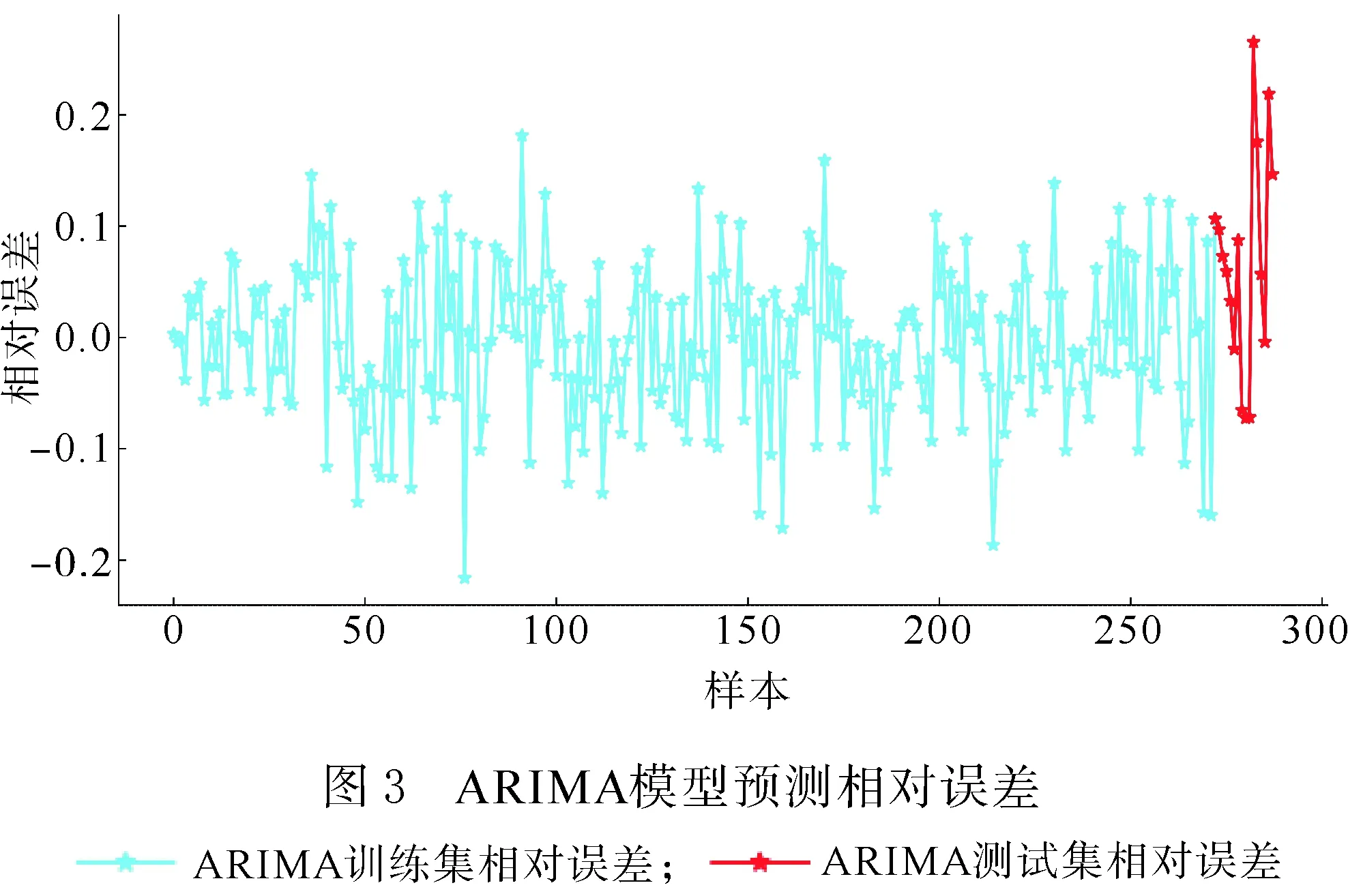
通过观察模型的正态性检验图(图2),可知,其正态性检验基本呈线性分布,表示模型训练效果好,因此确定最优模型为ARIMA(4,1,4)。利用交通流数据对模型进行仿真,其预测相对误差如图3所示。测试集前一部分数据相对误差较小,之后出现了一定的波动,但整体来看预测效果良好。
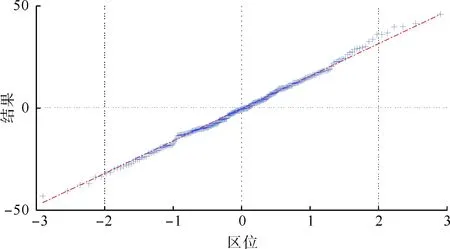
图2 正态性检验
1.2 SVM模型
SVM模型是基于结构风险最小化原理构建的,其预测模型函数表达式为
f(x)=w·φ(x)+b
(2)
式中:f(x)为预测函数;w为权重;φ(x)为非线性映射;b为偏置。
对于实际交通流问题存在许多影响因素,因此交通流数据一般为非线性[13],可以利用核函数对非线性以及难以区分的数据的处理能力,将样本从原低维的空间中通过核函数映射到高维空间加以区分,利用Lagrangian函数和对偶理论进行转换,并按照KKT(Karush Kuhn Tucker)定理对已转换的问题进行优化,其优化后的模型为
(3)
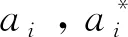
SVM模型常用的核函数包括线性核函数、径向基核函数、多项式核函数以及多层感知器核函数等,核函数的选取对SVM模型的学习及泛化能力有重要影响。通过经验选取适应度较好的径向基核函数:
(4)
为了提高模型预测精度,将数据特征转化为相同尺度,对所选用的交通流量进行数据归一化,选取数据中的最值通过缩放将其归一到[0,1]中,假设有M个样本{x1,x2,x3,…,xm},则
(5)
其中min(x)为M个样本中的最小值,max(x)为M个样本中的最大值,利用MATLAB数值仿真软件对其进行训练预测,并利用网格法寻找最佳的惩罚参数和核函数参数。
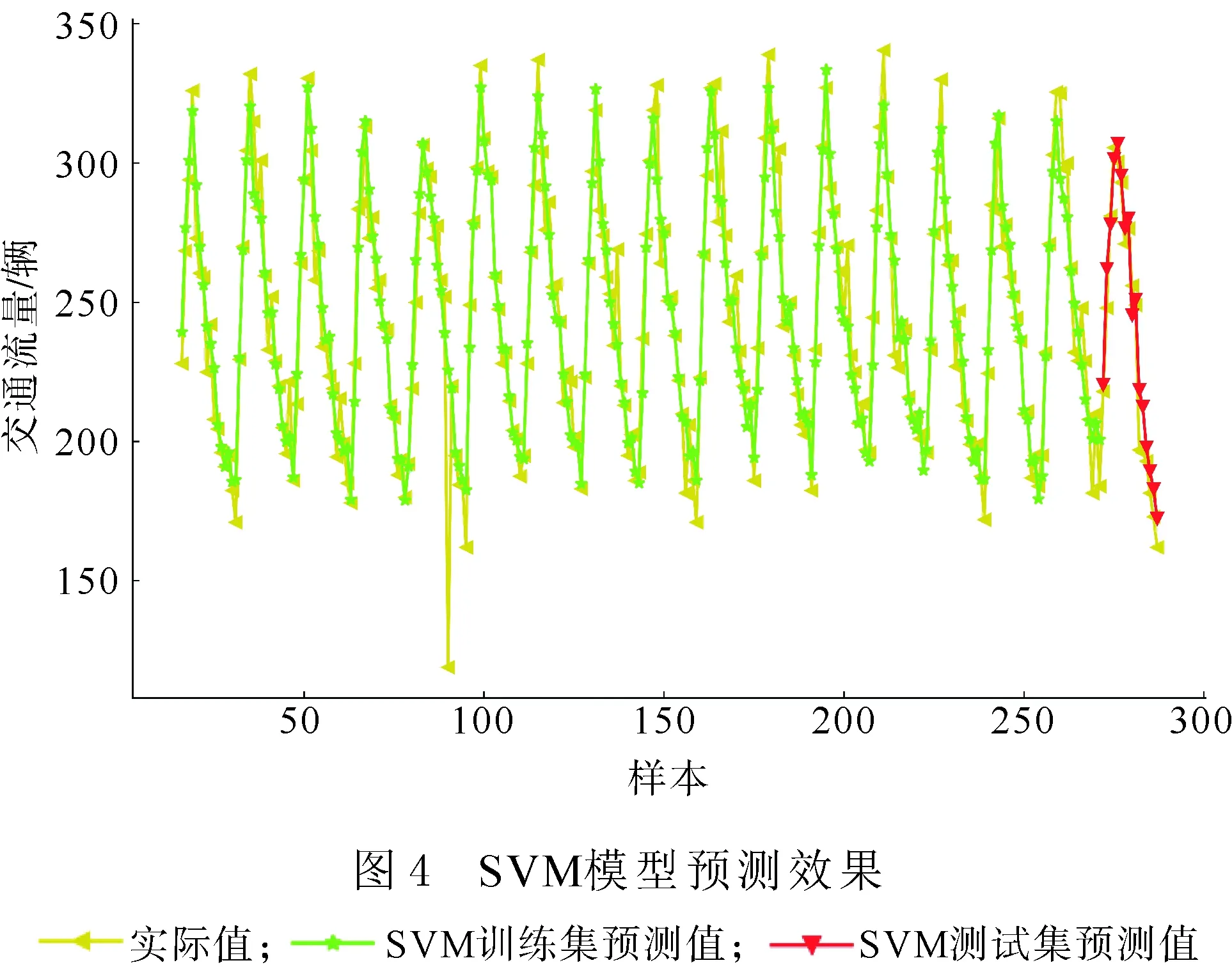
利用训练集归一化得到的数据对SVM模型进行训练,并导入测试集中的数据进行模型仿真,其预测结果与真实交通流量的相关性分析如图4所示。
判定系数R2的计算公式为
(6)
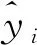
通常R2>0.75表示模型具有良好的拟合性和可解释性;而R2<0.5,表示模型拟合效果较差。通过仿真可知SVM模型的R2=0.943,其值接近1,表示该模型的预测精度较高,能充分捕捉交通流中的非线性特征。
2 ARIMA-SVM组合预测模型
考虑到交通流容易受多种因素干扰,既存在线性交通流特征,也存在非线性交通流特征,因此本文采取ARIMA-SVM组合预测的方法对交通流进行预测,首先对交通流量数据进行预处理后,然后利用ARIMA与SVM分别对交通流数据进行预测,最后对各模型的预测结果进行加权组合[14]。依据各个模型在预测结果中的误差大小来确定单一模型在组合模型中的权重,即在预测结果中的误差越大,则在组合模型中所占权重越小。组合模型能减少对实际交通流量的预测误差,提升预测精度,具体流程如图5所示。
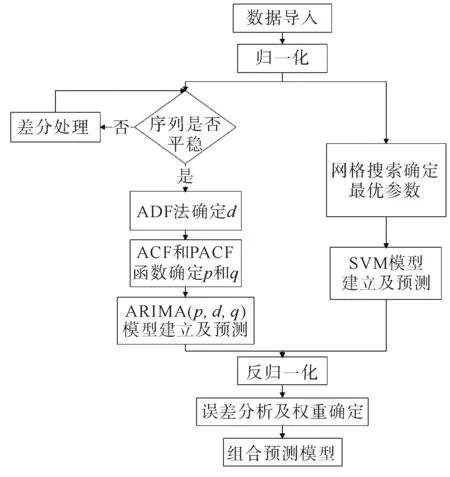
图5 模型流程
>以组合模型预测误差最小为原则,来确定最优权重组合。设
(7)
(8)
a+b=1
(9)
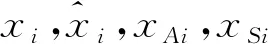
3 模型的数值仿真分析
3.1 数据来源与处理
对于短时交通流预测一般是指根据历史数据对未来时间的交通流量进行预测,通常其时间粒度不超过15 min。本文将道路横断面交通检测器15 min内检测到的交通流量作为模型输入,所用数据来自于西安市市区的交通流量[11],数据采集技术为视频采集,采集环境避开了大雨和大雾等不良天气。因为工作日人们的外出更具规律,所以选取16个工作日交通流量数据用于模型的训练和预测,采集时段为7:30—11:30,共288个数据。考虑到交通受外界因素影响时,如出现突发状况或交通检测器工作异常时,会导致数据的异常和丢失,将此类噪声数据用于模型的训练,会降低预测精度,因此,需要对异常的数据进行剔除,而丢失的数据使用前一天相同时间段的交通流数据进行补充。
数据集中共288个数据,前272个用于模型训练,即训练集,剩余的16个数据用于对模型的评价,即测试集。
3.2 评价指标
本文通过比较各模型的均方根误差ERMSE,以及平均绝对百分比误差EMAPE,可以得知训练后的模型在短时交通流量预测上取得的效果。
(10)
(11)
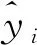
3.3 仿真结果
由于有多组预测值,因此权重确定函数以矩阵的形式表达,用MATALB数值仿真软件建模求解。得a=0.453887,b=0.546113。由式(7)计算可以得到2个单一模型的组合模型:
(12)
对比各个模型预测结果以及交通流量的真实值,如图6所示。
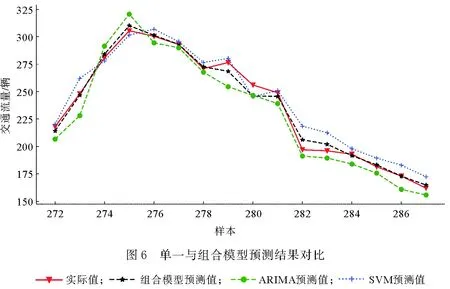
由图6可知,建立的3个模型都有较好的预测效果,都能拟合出交通流的趋势。就单一模型而言,交通流变化较大时,SVM模型相比于ARIMA模型能更好地捕捉交通流中复杂特征;交通流较为平稳时,ARIMA模型的预测效果更好。而组合模型兼顾了2个单一模型的优势,从图6中可以看出,在交通流平稳上升与下降阶段,组合模型的预测曲线与实际值曲线几乎重合;在其他阶段的预测效果依然优于单一模型的预测效果。
从表1中各个模型的评价指标可知,组合模型的2个评价指标均低于ARIMA模型和SVM模型,证明了组合模型的预测效果更好,在面对较为复杂的交通情况时,仍然有较高的预测精度。

表1 模型预测评价
4 结论
建立了一种关于道路横断面交通流量的ARIMA-SVM组合预测模型,经过对3个模型的预测结果对比得知,ARIMA预测模型的EMAPE为4.17,SVM预测模型的EMAPE为3.69,ARIMA-SVM组合预测模型的EMAPE为1.57。组合模型的EMAPE和ERMSE均小于单一模型,由此可知,相比于ARIMA模型的线性预测以及SVM模型的非线性、高维度和小样本数据预测,组合模型的预测结果要优于单一预测模型,该模型融合了2个单一模型的优势,对复杂道路交通流的预测得到了较好的效果。

