圆柱地层模型中超深方位电磁波仪器磁场信号模拟
李国玉,洪德成,岳喜洲,3,刘天淋,武圣哲,马明学
(1.中海油田服务股份有限公司油田技术研究院,北京 101149;2.吉林大学物理学院计算方法与软件国际中心,吉林长春 130012;3.电子科技大学电子科学与工程学院,四川成都 611731)
方位电磁波随钻测井技术可提供近百米内周向和前向电阻率分布信息,已成为复杂油气藏勘探开发的重要手段。自2005年斯伦贝谢(Schlumberger)公司推出的随钻方位电磁波测井仪器PeriScope[1],实现了井周5 m范围内地层边界及电导率各向异性测量,大斜度井/水平井中用于地质导向的方位电磁波测井方法与仪器制造进入快速发展期。紧随其后,贝克休斯(Baker Hughes)和哈里伯顿(Halliburton)公司分别推出了各自的商业化随钻仪器[2-3]。2018年中海油田服务有限公司自主研制了新型随钻方位电磁波电阻率仪器DWPR,并成功实现了上百口井的商业化地质导向作业,标志着中国自主研发的随钻方位电磁波电阻率测井技术跻身国际前列[4-5]。随着工业开发需求,近几年国际三大测井油田服务公司分别推出各自的超深随钻方位电磁波测井仪器,如Geosphere、EarthStar和VisitTrack,将周向探测深度逐步推进至80 m,实现了测井尺度与物探分辨率的尺度耦合[6-10]。国内科研院所也加快了相应的理论研究与新仪器研制[11-17]。超深随钻方位电磁波测井仪器采用倾斜线圈作为发射/接收天线,模块化设计,源距动态范围约5~40 m。在理论研究上,可将倾斜发射线圈等效为磁偶极子源,通过计算磁场分量空间分布模拟仪器响应随仪器参数及地层参数的变化规律。笔者利用圆柱状分层地层研究超深探测仪器井眼影响规律及径向探测特征。圆柱状分层介质结构简单,通常存在积分形式电磁场解析解。为了匹配圆柱边界条件,需在波数域中给出其解析递推公式。求解过程大致可分为以下3个方面:①直达场的波数域表达式;②场在分层介质中的传播;③由波数域到空间域电磁场的数值积分。在电法测井领域,早期Chew[18]引入系数矩阵求解电磁场,模拟仪器响应。其电磁场递推规则得到学者们广泛认可,进一步被应用在更为复杂的求解模型中,如考虑电导率各向异性、仪器偏心等[19-22]。上述文献工作更注重分层介质中电磁场递推表达式的求解,而鲜有直达场波数域表达式的求解过程。笔者从麦克斯韦方程组出发,给出三轴正交磁偶极子源电磁场完整求解过程。在描述场的传播方面,引入归一化广义反射系数,以解决Chew方法中的数值溢出问题;为提高数值积分的稳定性及计算精度,将波数域直达场与反射场分离,对应前者直接给出空间域代数解,后者采用三次样条拟合方法求解数值积分。最后,以超深随钻方位电磁波测井仪器Geosphere为例,考察仪器倾斜天线磁场信号随仪器源距、频率、井眼电导率、偏心距及地层电导率等参数变化规律。
1 正演计算方法
图1给出了共轴圆柱地层模型,最内层为井眼,向外依次为侵入带、原状地层等。考虑到真实作业环境,设定最内层钻井液电导率为各向同性,其余层为各向同性或单轴各向异性。忽略金属钻铤影响,将磁偶极子源置于最内层。根据矢量叠加原理,任意方向磁偶极子源激发的电磁场可由三轴正交磁偶极子源的电磁场张量通过矢量叠加得到,因此在正演计算中首先推导三轴正交磁偶极子源的电磁场,然后再通过矢量叠加得到任意方向发射-接收磁偶极子天线的磁场信号。

图1 井眼中的三轴磁偶极子源Fig.1 Triaxial magnetic dipoles in borehole
1.1 均匀介质中三轴磁偶极子的积分解
设电磁场的时间变化因子为exp(-iωt),空间域中的电磁场满足Maxwell方程:
(1)
(2)
其中
式中,M为磁偶极子强度;r′为发射位置;ε*为复介电常数;σ为电导率;μ为磁导率,在油气测井领域通常假定其为真空磁导率,即μ=μ0。对式(1)和(2)两端取散度,得
(3)
(4)
对式(1)和(2)两端取旋度,利用式(3)和(4)及微分运算规则××A=(·A)-2A,得
(5)
(6)
(7)
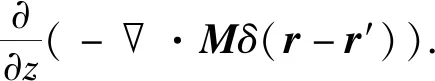
(8)
其中
k2=ω2με*.
首先,考虑无源区域方程(7)、(8)的解:
(9)
(10)
上述方程(7)、(8)通常在波数域中求解。电磁场空间域与波数域表达式满足如下变换关系:
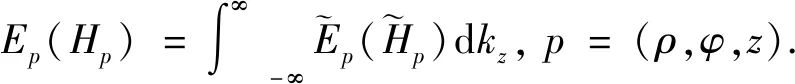
(11)
其中积分变量kz为垂直波数。结合式(9)和(10),并利用分离变量法,得任意ν阶模量表达式:
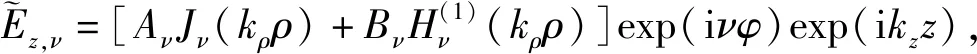
(12)

(13)

其次,求解电磁场横向分量。无源空间中式(1)和(2)的波数域方程满足:

(14)

(15)
在圆柱坐标系下,求解式(14),得其分量方程:

(16)
同理,求解式(15)得

(17)
联合式(16)和(17),并应用恒等式ez×(s×ezAz)≡sAz,ez×(ez×As)≡-As,得横向分量表达式:

(18)

(19)
将式(12)和(13)分别代入式(18)、(19),则进一步改写成如下简明的矩阵形式:

(20)

(21)
最后,考虑含源方程的解。引入符号M=Mpα(Mp为磁偶极子源分量,α为发射源方向),式(7)和(8)进一步改写为
(22)

(23)
其解为
Ez=-iωμMpα·ez×′g(r-r′),
(24)

(25)
其中
(26)

(27)
其中,ρ<是ρ和ρ′中较小的值,而ρ>是ρ和ρ′中较大的值。结合式(24)和(25),电磁场z分量表示为

(28)


(29)
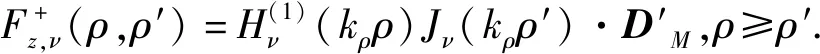
(30)
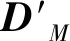

(31)
在柱坐标系下的其分量形式为

(32)
利用电磁场z分量表达式(28),结合式(20)和(21)可得到电磁场横向分量。
1.2 电磁场在分层介质中的传播
在最内层,电磁场z分量传播项表示为

(33)

(34)
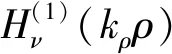
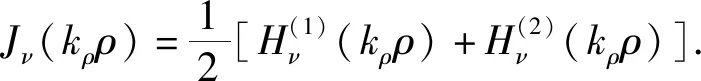
(35)

(36)
注意这里行波不同角模量彼此不耦合。由式(36)求解系数bν并代入式(33)和(34)得

(37)

(38)

(39)
结合式(38),并考虑到关系式(20)和(21),得横向分量反射场传播项:

(40)

(41)
其中

(42)

(43)
1.3 广义反射系数

图2 狭义反射/透射系数和广义反射/透射系数Fig.2 Local and general refection/transmission coefficients
反射/透射系数是为了便于描述电磁波在界面处传播特征所引入的物理参数,如图2所示,并通过电磁场连续边界条件求解其表达式。反射/透射系数的表达形式和物理含义因引入方式的不同而不尽相同,其中以物理图像清晰、表达优美者为最佳。本文中采用文献[23]的定义方式,引入归一化狭义反射/透射系数及广义反射/透射系数。
针对单一边界,归一化狭义反射/透射系数给定为

(44)
其中

(45)
其中

1.4 电磁场的数值积分
将式(39)代入式(28),得均匀介质中偶极子源产生的直达场积分表达式:

(46)
在数值计算中,无需计算该积分表达式,而是计算其空间域代数解,实时准确。将式(38)代入式(28),得柱面边界引起的反射场:
(47)

(48)
其中
β=cos[kz(z-z′)],
或
β=i·sin[kz(z-z′)],

同理,电磁场水平分量计算也有类似简化形式。此外,因为反射场被积函数收敛域比总场的小,所以将反射场与直达场分开计算的另一个优点是数值计算更稳定、准确。
数值计算精度除了与收敛域的大小有关,还与积分方法及被积函数形态有关。图3给出了被积分函数随自变量变化关系。可以看出,被积函数的震荡性主要来自于正余弦函数β(kz)。将除正/余弦函数外的其余部分定义为X(kz),分成若干区间,采用三次样条函数拟合。

(49)
求解系数Cj后,与正余弦函数结合,通过查找常用积分表即可实现快速、稳定的数值积分,例如:
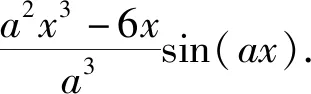
(50)
最后将所有区间的积分结果求和即得到空间域电磁场。

图3 被积函数形态特征Fig.3 Chatacterisitcs of integrand
2 随钻方位电磁波仪器响应


(51)
Hyx)]sin(2φ),
(52)
Hyx)]sin(2φ).
(53)
式中,φ为仪器自转角。

图4 随钻方位电磁波仪器偏心示意图Fig.4 Schematic diagram for an eccentric LWD azimuth resistivity tool in borehole
3 数值模拟分析
3.1 计算方法验证
考虑三层地层模型。最内层为井眼,半径为10.795 cm,电导率σ1=20 S/m;第2层为侵入带,半径为30.48 cm,水平电导率σh,2=0.5 S/m,垂直电导率σv,2=0.25 S/m;第3层为原状地层,水平电导率σh,3=1 S/m,垂直电导率σv,3=0.2 S/m。如图4所示,取发射-接收径向位置ρT=ρR=5.08 cm,源距L=2 m,频率f=20 kHz。空间域背景场分量由如下代数表达式求解:

(54)

(55)
Hxy=Hxz=Hyx=Hyz=Hzx=Hzy=0.
(56)
其中
k2=ω2με*.
反射场分量由其积分表达式求解。表1给出了数值对比结果,相对误差小于0.5%,验证了本文算法的正确性。

表1 解析算法与有限元方法计算结果统计Table 1 Results comparison between analytical algorithm and finite element method
3.2 磁场随仪器参数变化特征
选择两层模型,井眼填充盐水钻井液,电导率考虑极限情况σ1=50 S/m,井眼半径为10.795 cm。地层电导率水平电导率σh,2=0.1 S/m,垂直电导率σv,2=0.01 S/m。取ρT=ρR且很小,模拟仪器居中情况。图5给出了几组源距下接收天线R1磁场信号(本文图例中信号实/虚部强度均为绝对值)随频率变化关系。磁场实部号信号在低频时随频率变化关系不明显,当频率进一步升高时非线性关系明显增加,并出现“过零”现象。虚部信号在低频时随频率增加而增大,在把高频部分,类似实部信号,非线性关系明显增强,并出现“过零”现象。
接收天线R3与天线R2满足镜像对称关系,考虑到模型的圆柱对称结构,天线R3磁场分量随参数变化规律与R2相同,因此本文中只给出R2磁场分量随模型参数变化关系。图6给出了不同源距下接收天线R2磁场信号随频率变化关系。其响应特征与天线R1基本相同,但高频部分的磁场信号与频率的非线性关系更弱些。

图5 R1磁场信号随频率变化Fig.5 Magnetic field of R1 along with frequency
图7给出了接收天线R1在有/无井眼情况下磁场信号对比,可以看出,当频率小于50 kHz情况下,井眼环境对磁场实部几乎没有影响,当频率大于50 kHz,井眼环境对磁场有较明显影响。
图8给出了5和35 m两组源距下天线R1和R2信号强度的比较。非共面天线R2信号强度明显比共面天线R1信号大,说明非共面接收天线比共面接收天线磁场耦合能力强。虽然磁场虚部信号出现多次“过零”现象,非线性关系复杂,但总体上也还是非共面天线R2信号强度比共面天线R1信号强度大。
图9分别给出12和96 kHz两组频率天线R1和R2磁场强度随源距变化。可以看出,非共面天线R2磁场信号强度比共面天线R1的大,且随源距增加时非线性关系较弱。

图6 R2磁场信号随频率变化Fig.6 Magnetic field of R2 along with frequency

图7 井眼对R1磁场信号的影响Fig.7 Influence of borehole on magnetic field of R1

图8 R1与R2磁场信号随频率变化Fig.8 Magnetic field of R1 and R2 along with frequency
3.3 磁场随仪器偏心参数变化
考虑如下3组参数:f=10 kHz,L=35 m;f=24 kHz,L=8 m;f=96 kHz,L=5 m,分别模拟共面天线R1和非共面天线R2随偏心距、仪器自转角、井眼钻井液电导率、地层电导率变化关系。
图10给出了仪器沿发射天线所在平面(x轴)偏心时共面天线R1随偏心距变化关系。可以看出高频短源距(f=96 kHz,L=5 m),磁场信号受偏心影响较大,而其他两组因为源距较长频率较低,实部/虚部信号受偏心影响均很小。图11给出了非共面天线R2磁场信号随偏心距变化关系。对比图10发现,R1与R2受偏心影响规律基本相同。总体来讲,仪器沿发射天线所在平面偏心,偏心距影响不大。
随钻仪器在测量过程中会绕自身旋转。假定偏心距离d=2.22 cm。图12和13给出了R1和R2的磁场信号随自转角变化规律(仪器沿非发射方向偏心与仪器自转具有等价性)。较短源距(L=5、8 m),磁场信号都有“过零”现象,且幅度变化很大,说明仪器偏心对磁场信号影响不可忽略。在后期资料处理中,需要考虑偏心因素造成的影响。
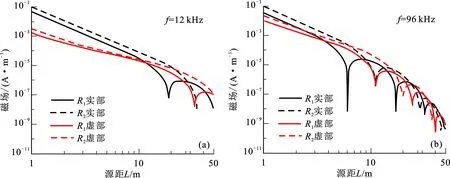
图9 R1和R2磁场信号随源距变化Fig.9 Magnetic field of R1 and R2 along with source distance

图10 R1磁场信号随偏心距变化Fig.10 Magnetic field of R1along with eccentric distance

图11 R2磁场信号随偏心距变化Fig.11 Magnetic field of R2 along with eccentric distance
3.4 电导率变化对磁场信号的影响
图14给出了共面天线R1磁场信号随钻井液电导率变化规律。可以看出当井眼钻井液电导率小于10 S/m时,磁场信号几乎不随钻井液电导率变化,受其影响很小;而当钻井液电导率大于 10 S/m时,磁场信号有轻微变化。
图14和图15给出了共面天线R1和非共面天线R2磁场信号随地层水平电导率变化规律,保持各向异性比值不变。可以看出地层电导率比井眼钻井液电导率对磁场信号影响大得多,而且当电导率大于0.1 S/m时,磁场信号会出现连续“过零”现象,非线性关系更加复杂。非共面天线R2磁场信号具有相似的变化规律。

图12 R1磁场信号随自转角变化Fig.12 Magnetic field of R1 along with rotation angle
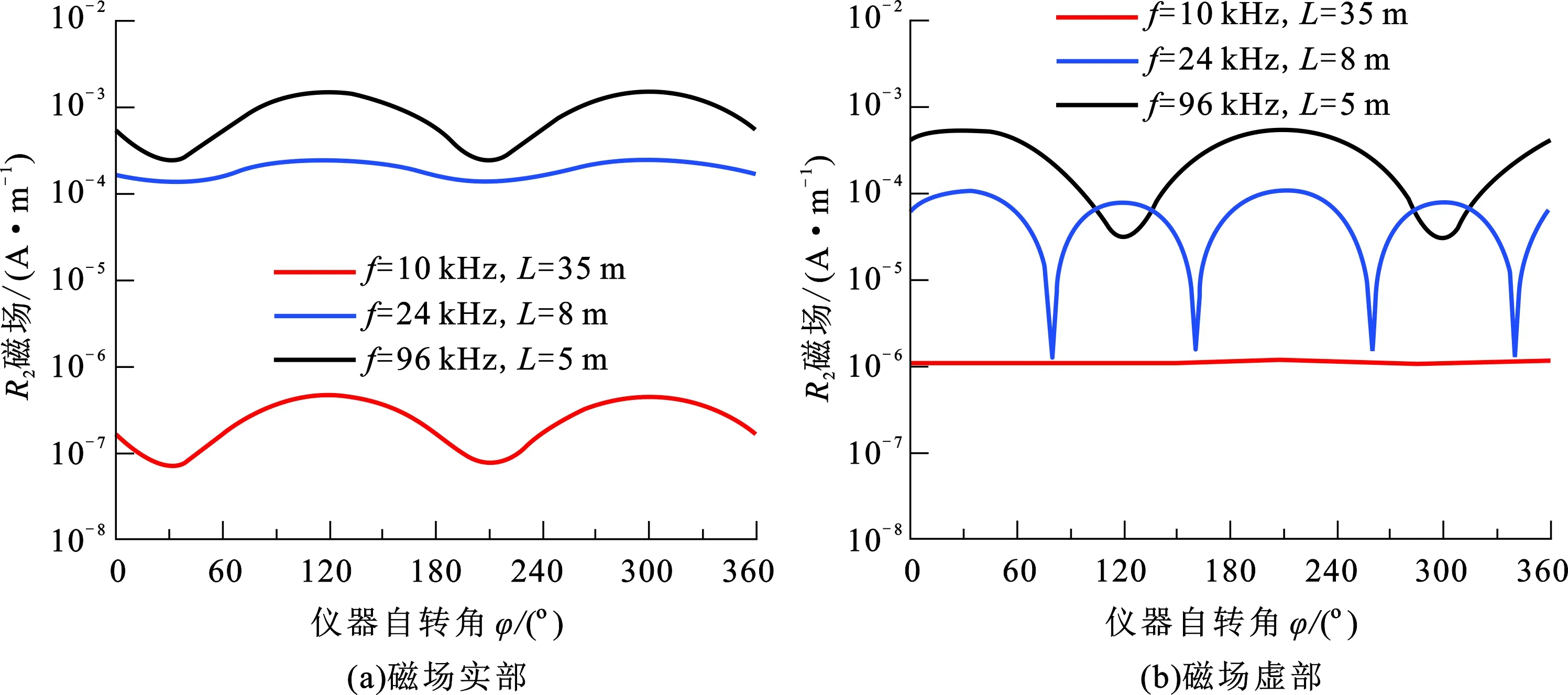
图13 R2磁场信号随自转角变化Fig.13 Magnetic field of R2 along with rotation angle

图14 R1磁场信号随井眼电导率变化Fig.14 Magnetic field of R1 along with borehole conductivity

图15 R1磁场信号随地层电导率变化Fig.15 Magnetic field of R1 along with formation conductivity
4 结束语
针对圆柱状分层地层,从麦克斯韦方程组出发推导了三轴正交磁偶极子源积分解析解表达式,结合归一化广义反射系数求解井眼内部电磁场分布。利用矢量叠加原理给出任意方向发射-接收天线磁场分量表达式,模拟随钻方位电磁波电阻率仪器磁场信号随发射频率、源距,井眼电导率、偏心距及地层电导率变化规律。数值模拟结果显示:非共面发射-接收天线测量到的磁场强度比共面发射-接收天线的强度大;井眼钻井液电导率对磁场信号影响不明显;地层电导率较大时磁场信号出现震荡的非线性关系;沿发射天线所在平面偏心对仪器磁场信号影响不明显;在偏心状态下绕仪器自身旋转测量,磁场信号与自转方位角变化关系复杂。

