基于分解策略的多标签在线特征选择算法*
张 永 伟,朱 祁,吴 永 城
(1.南瑞集团(国网电力科学研究院)有限公司,江苏 南京 210003;2.南京南瑞智慧交通科技有限公司,江苏 南京210032)
0 引言
近年来,随着多标签分类问题的深入研究,出现了大量的多标签分类算法[1-2]。目前,在多标签分类中,存在四种主要的处理策略:数据分解法、算法扩展法、混合法和集成法[3-4]。特征选择是多标签分类问题中的一个重要课题,并且已经进行了广泛研究。对于分类,特征选择的目标是通过相关特征的一个子集来构建有效的预测模型,通过消除不相关和冗余特征,可以减轻维度灾难的影响,提高泛化性能,加快学习过程,提高模型预测的性能。特征选择已在许多领域得到应用,特别是在涉及高维数据的问题中。
虽然已经进行了广泛研究,但大多数现有的特征选择研究都局限于批量学习,假定特征选择任务是以离线/批量学习的方式进行的,而且训练实例的特征是先验的。这样的假设并不总是适用于训练样本以顺序方式到达的实际应用。与批量学习方式相比,在线学习方式[5]则采用增量的方式处理数据集,相对而言,计算代价要小于批量学习算法。在现有的多标签在线分类算法中计算数据的全部特征信息是需要代价的。尤其是存在高维数据和数据冗余时,传统的多标签在线分类算法,需大量计算且分类性能较差。本文利用在线学习的优势,研究了多标签在线特征选择问题,旨在通过有效地探索在线学习方法来解决多标签特征选择问题。具体而言,多标签在线特征选择的目标是研究在线分类器,其仅涉及用于分类的少量和固定数量的特征。当处理高维度的连续训练数据时,如在线垃圾邮件分类任务(其中传统的批量特征选择方法不能直接应用),在线特征选择尤为重要和必要。
本文提出一种基于分解策略的多标签在线特征选择算法——MLFSGD算法。该算法采用二类分解策略,将多标签特征选择问题分解为二类特征选择问题,然后应用二类在线特征选择算法,完成多标签在线分类任务。通过多标签特征选择得到更好的特征子集,能高效地处理高维稀疏数据集。通过实验比较,结果显示本文提出的MLFSGD算法能够有效地降低数据维度,同时算法的分类性能也优于其他多标签在线特征选择算法。
1 相关工作
在机器学习算法中,在线学习是一类高效且扩展性较好的方法,这种增量的方式使在线学习能够有效地应对数据规模较大的分类任务。其中,感知器算法是一种简单、经典的在线学习方法[6],它通过预测样本标签与真实的样本标签是否相等,然后根据损失函数的大小,以梯度下降的方式求解并更新分类器模型。随着在线学习方法的深入研究,大量的单标签在线分类算法被提出[7-8]。其中,OGD算法是以在线梯度下降算法优化不同的损失函数定义的目标函数。CW算法则通过最小化新的权值向量分布与之前的权值向量分布之间的KL散度(Kullback-Leibler Divergence),来保证正确分类的概率大于设定的阈值,该算法采用一个比较主动的方式更新权值向量的分布,可以实现快速更新模型。SCW算法则克服了CW算法线性不可分、数据和噪声不敏感的缺点,通过在CW算法模型中加入了惩罚项,提高算法分类性能。
相比单标签在线分类问题,多标签在线分类问题的研究则更为复杂,也更符合现实应用。文献[9]用二类相关分解策略,结合已有的二类在线“被动-进攻”主动学习算法,提出基于分解策略的多标签在线“被动-进攻”主动学习算法。文献[10]同样利用二类分解策略,提出一种基于判别采样和镜像梯度下降规则的多标签在线主动学习算法,从而更有助于分类器收敛到最佳状态。
尽管相关文献对多标签在线分类算法进行了研究,但大多数多标签在线分类算法都需要访问数据样本的所有特征[11-12]。因此,为了降低模型学习成本和计算代价,在不影响模型的预测能力的前提下,有学者提出使用特征选择方法[13-14]以降低学习成本和计算代价。依照不同的选择标准,可以将多标签特征选择方法分为三种:过滤(filter)法,包裹(wrapper)法和嵌入式(embedded)法[15-16]。过滤法是在分类算法开始之前通过测量样本特征与类标签之间的相关性产生特征子集。包裹法依赖于预定的分类算法的性能来确定最优特征子集。包裹法针对特定模型,易于产生较高的分类性能,但在计算上通常比过滤法花费更大代价。嵌入法旨在将特征选择过程嵌入到分类器训练过程中,将特征选择和分类同时进行。它们通常比包裹法更快并且能够为学习算法提供合适的特征子集。
目前,有关多标签在线特征选择算法的文献很少。本文利用在线学习的方式,只允许分类模型访问少量或固定数量的特征,其目标是从高维的多标签稀疏数据集中学习线性分类器,进而解决特征选择问题,并对分类模型中的非零元素的数量进行严格的约束。本文提出的在线特征选择算法采用二类分解策略,将多标签分解成多个独立的二分类问题。该策略简单高效、计算代价低。在实验中采用5个评价指标进行比较,结果显示MLFSGD相比其他算法都有比较好的性能,尤其是在特征数较多的数据集上,优势更加明显。
2 多标签在线特征选择算法
本文在处理多标签特征选择问题时,设样本标签的集合为Q={1,2,…,q},q表示样本标签个数;假设样本X所对应的相关标签集合L⊆2Q。给定一个大小为N且独立同分布的训练样本集合D:

另外,标签集合也可以表示成二进制的形式:

其中,第i个样本对应的标签也可以表示为一个二进制标签:yi∈{-1,1}q,1表示样本Xi包含该标签,-1表示不包含该标签。
2.1 二类分解策略
多标签分类算法中,二类分解策略(Binary Relevance,BR)是一种数据分解的方法,将多标签分类问题分解成q个相互独立的二类分类问题。对于一个标签集合为Q={1,2,…,q}的多标签分类问题,在二类分解方法中,被分解为q个二类分类的问题,每一个二类分类问题对应标签集合Q中一个可能的类别标签。
二类分解的过程是首先为标签集合中的每一个标签建立对应的二类的训练集合,对于第j个类别标签,可以将训练样本集合分解为如下形式:

其中yj为-1或1,-1表示不是样本的相关标签,1表示是样本的相关标签。接着,BR方法利用单标签分类的二类分类算法来训练一个二类分类器hj。这样,就会产生q个二类分类器,每一个多标签训练集D中的样本都将参与这q个分类器的分类过程。在二类分类器hj中,如果样本Xi与标签j相关联,则被作为一个正类的样本,否则,被作为一个负类的样本,在预测阶段,将未知标签的样本在每一个二类分类器中的预测结果结合起来,就可以得到预测出的未知样本的标签集合Lq,并且满足:

与其他的多标签数据分解策略方法相比,BR方法不仅简单有效,而且计算代价较低。不仅如此,二类相关分解方法假设标签之间是相互独立的,对标签的添加或删除都不会对剩余的其他标签产生影响,对某一个标签的训练和预测也不会对其他标签的分类过程产生影响,这样有利于在线实现该方法。因此,BR方法适合于处理大规模的多标签分类问题。
2.2 二类在线特征选择(OFS)算法
二类在线特征选择OFS算法[17]是基于向量的分类器模型W∈Rn,其中最多包含B个非零元素,采用形式sign(W·X)表示,其中向量W中的每个元素表示分配给每个样本Xt的特征权重。在t时刻,OFS算法的权重为Wt,yt(Wt·Xt)表示预测函数。
当预测值大于0时,分类器预测正确。为了更好地预测样本标签,OFS算法使用在线梯度下降(OGD)算法来优化模型W。
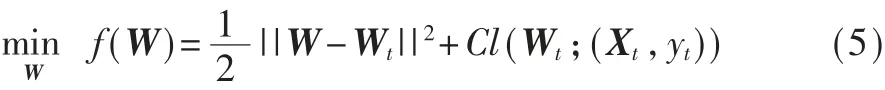
其中,C〉0是惩罚参数,损失函数为铰链损失(hinge loss):

t时刻,分类器更新模型,其中η表示学习率:

为了更好地进行特征选择,在更新模型中使用截取函数,确保更新分类器模型W中的元素是最大的B个元素。算法1给出了截取函数的具体步骤。

2.3 基于分解策略的多标签在线特征选择算法
结合二类分解策略,本文提出了基于分解策略的多标签在线特征选择算法——MLFSGD算法。在多标签在线分类算法中,分类器以在线学习的方式预测样本Xt的标签集合,最后根据样本标签的真实集合计算损失来判断分类器是否更新。然而,对于大数据量的数据集而言,这些数据具有复杂化与高维化的特点,尤其对于稀疏数据集而言更是存在着大量的冗余性和无关性的特征。而这些特征增加了机器学习算法的复杂度和运行时间,同时降低了模型预测的准确性。为了解决以上问题,本文使用在线特征选择的处理方式。对于多标签数据集,每个样本都包含多个标签,本文在不考虑标签相关性的条件下,使用分解策略将多标签特征选择问题分解成二类特征选择问题。具体地,MLFSGD算法首先初始化权重矩阵:

在t时刻,对于样本Xt,MLFSGD算法首先计算其预测函数:

其中,sign(·)表示符号函数。利用分解策略方式,分类器将样本Xt分解成q个独立的二类在线OFS算法。每个样本Xt含有q个标签,在t时刻,如果分类器预测样本Xt错误,则更新分类器权重Wt,j:

然后,根据投影公式对分类器做二次操作:

最后,利用截取方法选择B个特征。算法2概括了MLFSGD算法的具体步骤。

3 实验结果与分析
3.1 实验设置
实验中采用了MuLan提供的多标签分类数据集,数据主要集中在文本、视频和图像等领域。表1列出了六个多标签基准数据集(Mediamill、Scene、Delicious、Bibtex、Rcv1v2和Tmc2007)的详细信 息。本文采用了5个多标签评价指标(汉明损失(Hamming loss)、覆盖率(coverage)、排序损失(ranking loss)、平均精度(average precision)和1-错误率(one error))来进行算法性能的比较。其中,为了方便表示,对于覆盖率指标,将该指标结果做了归一化处理,即将覆盖率数值除以数据集的标签数。
本文在操作系统Windows 10环境中进行实验,使用MATLAB2018b开发编码。实验中,将所选特征的数量设置为每个数据集的10%(0.1×维度),正则化参数λ设为0.01,学习率η设为0.2。所有多标签在线算法都使用相同的参数。对所有实验数据集进行10次随机排列,然后对结果进行平均得到最终实验结果。
本文使用三个基于特征选择的多标签特征选择算法:MOFS[18]、MLPEtrun和MLRAND与本文提出的MLFSGD算法进行比较。MOFS算法是将多标签数据集划分为多个单标签数据集的一种在线特征选择算法,解决不平衡数据集的分类性能问题。MLPEtrun算法是基于感知器的多标签算法,利用分解策略,将基于感知器的特征选择算法推广至多标签分类。MLRAND算法采用随机查询的方式,随机选择固定数量的特征值,并利用分解策略来解决多标签分类问题。
3.2 实验结果与分析
本文首先在两个特征数较多的Rcv1v2和Tmc2007数据集上,给出汉明损失、平均精度、1-错误率和覆盖率四种指标的比较结果,如图1和图2所示。其中图1表示四种算法在数据集Rcv1v2上四种不同评价指标的比对结果。可以看出本文提出的MLFSGD算法优于其他算法。图2表示四种算法在数据集Tmc2007上不同评价指标的对比结果,可以看到在评价指标1-错误率和平均精度上,MLFSGD算法明显优于其他算法,在另外两种指标中,MLFSGD算法优于MOFS算法和MLRAND算法,仅次于MLPEtrun算法。同时可以看到随着选择特征比例的不断增加,所有算法的分类性能没有特别明显的提升,这也证明特征选择的优势。

图1 四种算法在Rcv1v2上的比较结果

图2 四种算法在Tmc2007上的比较结果
为了更好地评估本文提出的MLFSGD算法,表2~表6给出了在六个数据集上四种算法的实验结果。
表2是四种算法在六个不同数据集上的汉明损失值。可以看出,MLFSGD算法取得比较低的值,尤其在数据特征数比较大的Tmc2007和Rcv1v2数据集上,MLFSGD算法的汉明损失值小于MOFS和ML RAND算法。表3所示为四种算法在不同数据集上的1-错误率值,在六个数据集上除了Delicious数据集以外,MLFSGD算法都取得最小的值,特别是数据集Tmc2007和Rcv1v2。表4是四种算法的排序损失值,MLFSGD算法在大部分数据集上为最优,其中,在Tmc2007数据集上,MLPEtrun算法要优于文本提出的MLFSGD算法。表5所示为四种算法的覆盖率值,从表中可以观察到,MLFSGD算法除了在Tmc2007数据集次优之外,其他数据集上结果最优。表6所示为四种算法的平均精度值,MLFSGD算法在所有数据集上均为最优。通过以上实验证明,本文提出的MLFSGD算法在做多标签在线特征选择时能够取得比较好的结果。

表2 四种算法在六个数据集上的汉明损失

表3 四种算法在六个数据集上的1-错误率

表4 四种算法在六个数据集上的排序损失
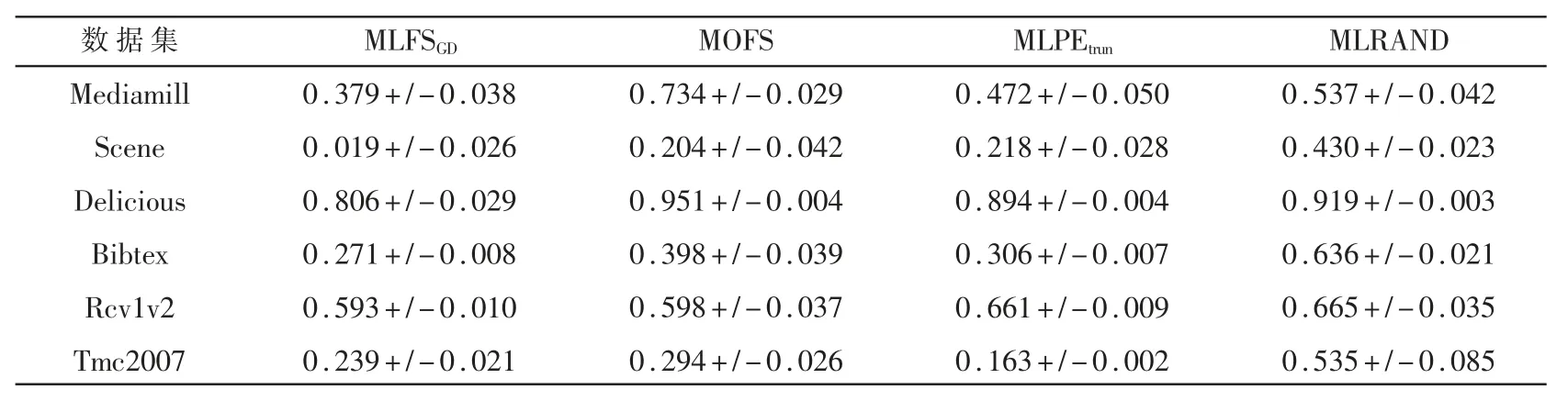
表5 四种算法在六个数据集上的覆盖率

表6 四种算法在六个数据集上的平均精度
4 结论
本文提出了基于分解策略的多标签在线特征选择算法,将多标签在线特征选择问题分解成多个二类在线特征选择问题,进而对样本进行特征选择。实验基于六个数据集,使用不同的多标签评价指标,比较MLFSGD算法和其他三种在线特征选择算法在特征子集个数从10%增加到100%时的性能。实验表明,MLFSGD算法在处理多标签在线特征选择时,性能优于其他在线算法。由于该算法假设样本之间相互独立,并没有考虑样本标签相关性,未来工作中,将就标签的相关性进行进一步研究。

