10倍变焦安防镜头光学系统设计
宋鹏飞,王春艳,孙昊,王志强,刘欢
(1.长春理工大学 光电工程学院,长春 130022;2.江苏北方湖光光电有限公司,无锡 214000)
安防镜头是维护国家安全、保护居民生命财产不受侵犯的重要设施,在各种场合都有安防镜头的身影[1]。在各种安防镜头中,用于停车场车辆监控的安防镜头因为车辆不断增多,成为各安防镜头公司研发的方向。2007年,胡际先设计了一款75~900 mm的连续变焦系统,F数为4~6.4[2]。2013 年,张齐元等人[3]设计出一款 6~60 mm的连续变焦系统,最大F数为2.4。2015年,姚清华等人[4]设计出10~500 mm的变焦镜头,但使用了非球面。2018年,白虎冰等人[5]仿真了一款F数为8的100~600 mm的光学变焦系统。2019年,张建[6]设计了 30~300 mm的轻型变焦距系统,F数为3.5,同时使用了6片非球面,3片光学塑料。通过对上面例子的研究,为目标停车场设计了一款18~180 mm的变焦系统,用于停车场的车辆监控与车牌识别,在满足焦距的情况下,将F数缩小至2.2,用来增大通光量,并且全部采用国产球面镜以降低成本。
1 系统参数及设计方法
1.1 设计参数
本设计选用的成像器件为130万像素,1/2英寸的CCD,靶面尺寸为6.4 mm×4.8 mm,对角线长度为 8 mm,像元尺寸为 5 μm×5 μm。根据像元尺寸大小可确定传递函数的奈奎斯特频率为:
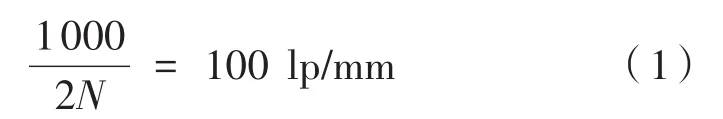
视场满足以下公式:

式中,θ为视场角;f为焦距;l为相机像面对角线长度。设计要求的相应技术参数如表1所示。
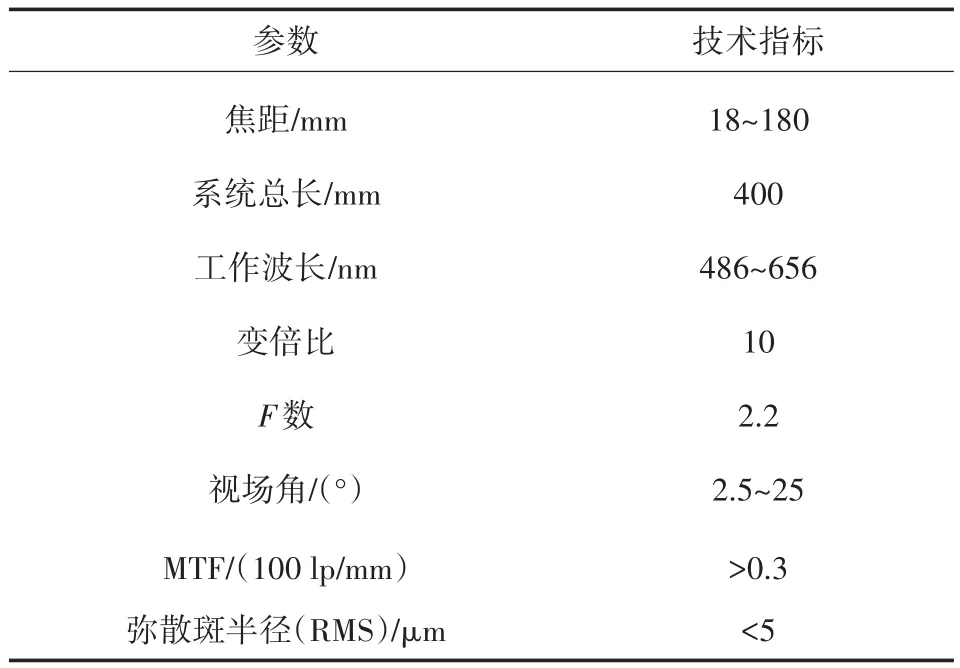
表1 光学设计参数
1.2 设计方法
变焦系统有光学补偿、机械补偿、双组联动和全动型四种方式。其中,机械补偿方式成像更清楚且像面移动小,机械结构更容易实现而被普遍使用[7]。机械补偿变焦光学镜头一般由前固定组φ1、变倍组φ2、补偿组φ3和后固定组φ4组成,如图1所示。变倍组φ2和补偿组φ3各自按照不同的运动曲线移动,从而达到焦距不间断变化[8]。目前,主要通过两种方式确定变焦系统的结构:一种利用高斯解与P、W、C法,但是其因为计算复杂,容易出错,故只适合简单结构[9];另一种是对合适的专利或者文献在光学设计软件(Zemax、CodeV、OSLO等)中进行适当缩放,再利用各种操作数进行仿真优化获得最终结果。这种方法可以使复杂的光学结构更加简单地得到好的结果。根据本文情况应选用的是后一种方法,找到了一个美国的专利进行修改使用[10]。
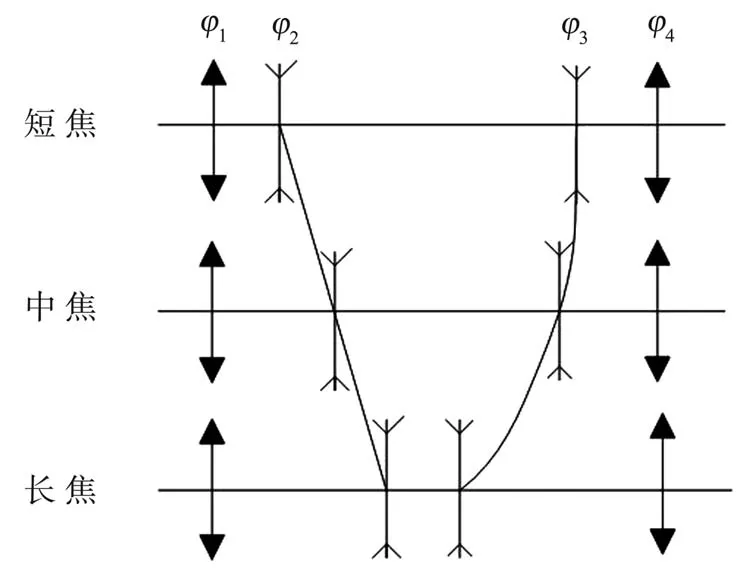
图1 机械补偿式变焦光学系统原理图
2 设计过程及像质评价
2.1 设计过程
本文确定采用正组补偿的机械变焦形式,设计出10倍连续变焦、高像质的变焦镜头,在200 m的监控距离以内,可监控的实际面积为70 m×50 m,适用于停车场安防。中国普通轿车车辆大小为长 3 800~4 300 mm,宽 1 600~1 800 mm,高1 400~1 600 mm。根据网上查到的数据,中国民众使用的民用车牌大小为140 mm×440 mm。一个镜头识别一辆车至少需要21×21个像素点[11-12],现在按照车子高为1 400 mm计算长焦与短焦识别一辆车的最远距离。一个镜头识别出车牌的字母与数字,车牌宽度至少为80个像素点,依据公式可以计算出识别的距离。公式为:

式中,f为系统焦距;R为物体的识别距离;a为检测目标的尺寸;d为像元尺寸;n为所需像元个数。
由上式可以算出,长焦识别车牌的最远距离为63 m,长焦识别车牌的最近距离为5.25 m,短焦时能识别一辆车的最远距离为240 m,短焦识别一辆车的最近距离为5.25 m,短焦在200 m范围内能看到的范围为71 m×53.3 m。所以该设计满足在目标停车场短焦识别车辆,长焦辨认车牌的要求。除此之外,人脸长一般为23 cm,要满足人脸识别一般脸长需至少占用45个像元尺寸,根据式(3)计算,在长焦时最远184 m可以辨别人脸,进一步保障了停车场人员与财产的安全,并在发生事故时提供证据。
前固定组为正光焦度,3片球面透镜能提供足够的工作距离,并平衡后固定组之前的像差,减轻后固定组校正压力。变倍组为负光焦度,通过移动3片球面镜达到倍率改变的目的。用来补偿像面移动的补偿组为正光焦度,由3片球面镜组成。后固定组由6片球面镜组成,为正光焦度,利用冕牌与火石玻璃组合进行残余像差校正。本设计的系统在18~180 mm焦距范围内进行变化,成像波段为可见光波段,10倍内实现连续变焦,系统结构如图2所示。图中由左到右分别是短焦、中焦、长焦3种状态下的光学系统图。其由15片透镜组成,总长为400 mm,最大半口径为59 mm,后截距为9.5 mm。

图2 变焦系统结构图
2.2 像质评价
2.2.1 传递函数
调制传递函数(Modulation Transfer Function,MTF)能根据MTF值的大小得出成像质量的好坏,是评价光学系统优劣的重要依据。利用Zemax仿真可以得到变焦镜头在短焦(18 mm)、中焦(100 mm)、长焦(180 mm)3种状态下的MTF曲线,如图3所示。系统在短、中、长焦时均能呈现良好的像,在20 lp/mm空间频率时MTF>0.85,50 lp/mm空间频率时MTF>0.55,100 lp/mm空间频率下MTF>0.3,全部满足要求。由以上数据可得出,物体最后的成像清晰,有利于停车场上车牌的识别。
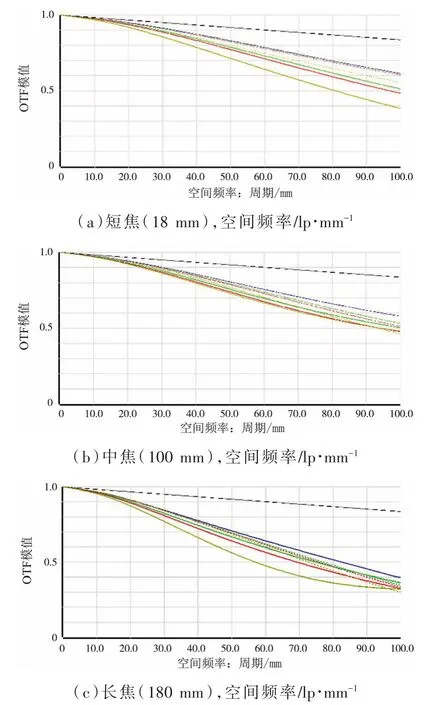
图3 各组态下调制传递函数
2.2.2 点列图
弥散斑半径是重要的成像质量参数,要使系统能有好的成像,弥散斑不能超过允许值,各组态下弥散斑半径如表2所示。由表2可知,系统中各组态RMS弥散斑半径均小于5 μm,可以看出整个系统在各焦距位置的成像都可以满足要求。
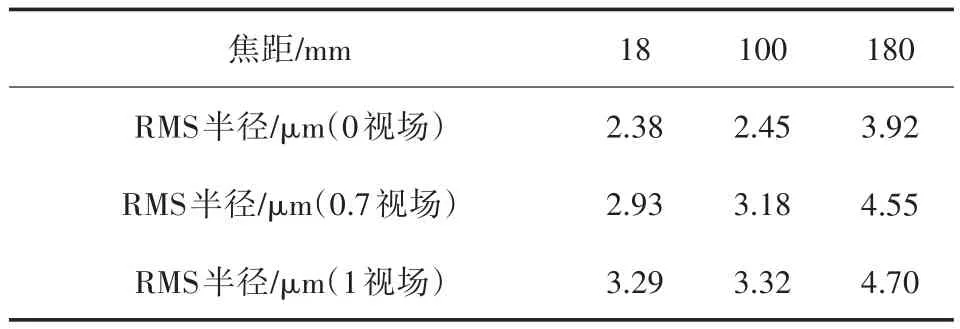
表2 各组态下弥散斑半径
2.2.3 场曲、畸变图
系统畸变、场曲曲线如图4所示。其中图4(a)—图4(c)分别为短焦、中焦、长焦的场曲、畸变图。由图4可知,除短焦畸变在3%,当系统处于中焦和长焦位置时,系统畸变均小于0.2%。系统场曲均小于0.04 mm,满足系统对变焦镜头的成像要求。
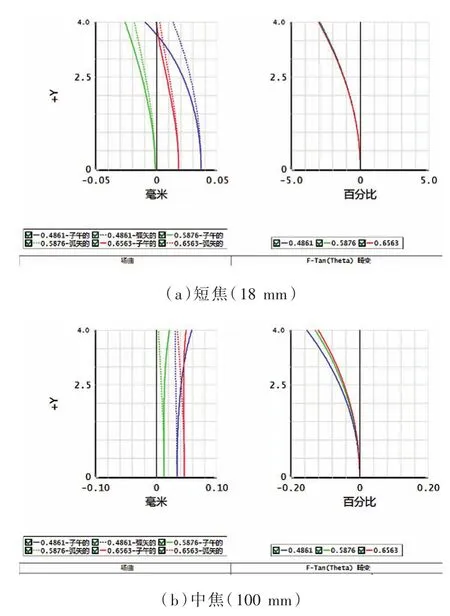

图4 各组态下场曲和畸变图
2.3 变焦补偿曲线
由变焦补偿曲线可以得知变倍与补偿过程是否合理,所以绘制变焦补偿曲线是机械变焦系统不可或缺的一步[13]。本设计利用动态光学理论可以得出变倍补偿曲线的公式[14]。公式为:
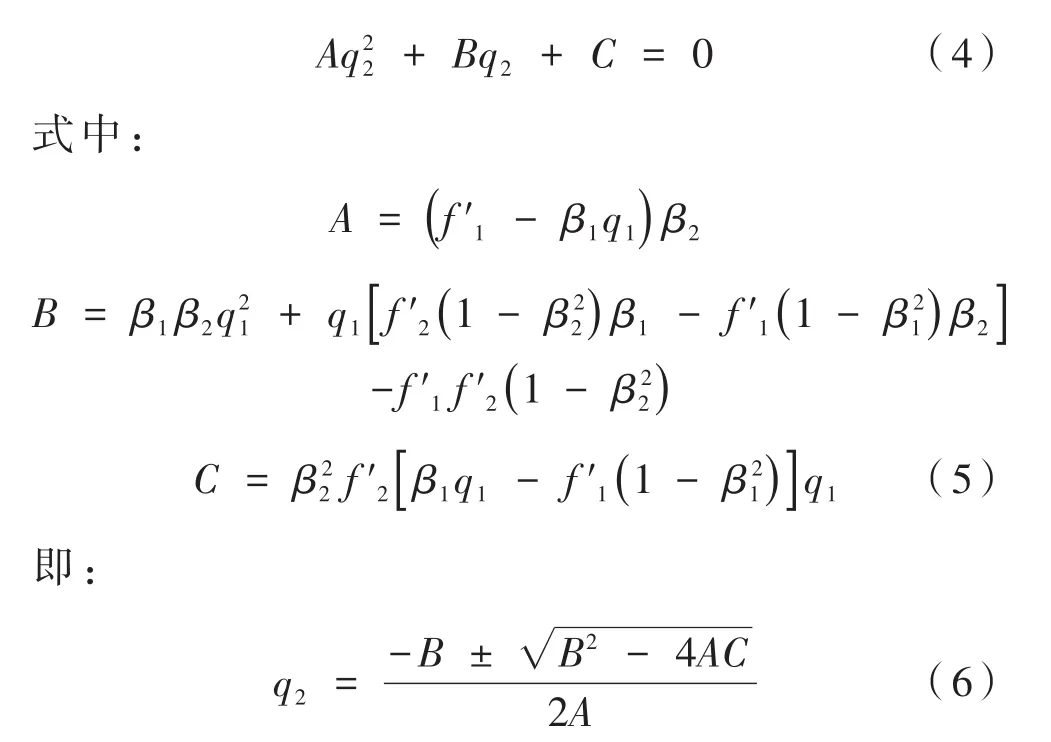
其中,β1、β2为变倍组与补偿组初始位置的垂轴放大倍率;q1、q2为变倍组与补偿组的位移量;f'1、f'2为变倍组与补偿组的焦距。
由上述公式准确计算出补偿组的运动曲线,再利用Matlab来拟合出变焦补偿曲线[15],如图5所示。横坐标代表变倍组与补偿组的光轴移动量,纵坐标代表沿着凸轮表面逆时针的旋转量。当进行变焦时,旋转凸轮,使变倍组进行焦距变化并进行线性运动,补偿组来完成像面补偿并作非线性运动。变倍组和补偿组的移动距离分别为237.393 mm和12.206 mm。变焦曲线并未出现断点,利于凸轮加工。
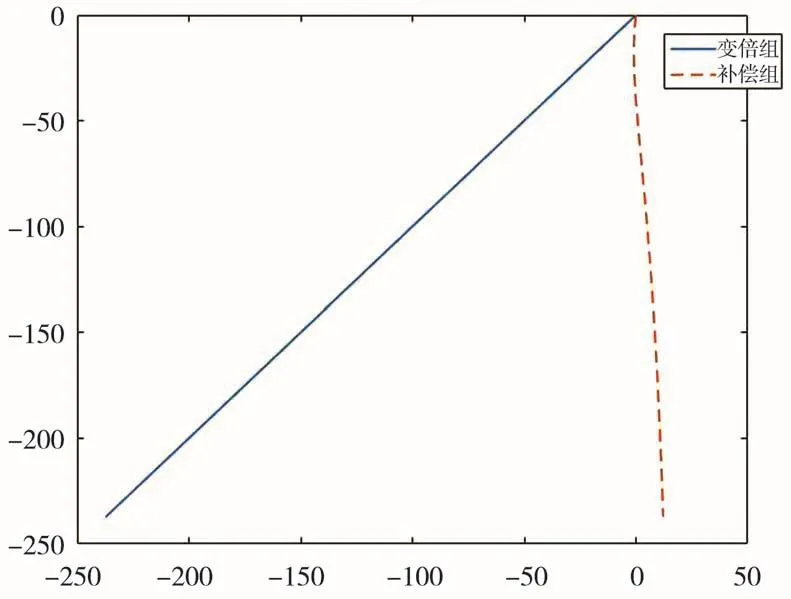
图5 变倍补偿曲线
3 结论
根据小型停车场的复杂环境,本文为此设计了10倍变焦距系统。通过选取合理的初始结构,并使用Zemax对光学系统进行像质优化,优化过程全部采用了国产玻璃,且未使用非球面,大大降低了制造成本。经过优化的变焦镜头具有较好的成像质量,可供安防及监控使用。此外通过对变焦理论的研究,结合动态光学理论在Matlab中绘制出变焦补偿曲线,证明了变焦运动的合理性。本光学设计的完成也为后面的机械结构设计奠定了基础。

