基于SWMM的城市社区尺度管网排水模拟——以福州市某排水小区为例

叶陈雷,徐宗学,雷晓辉,陈阳,李鹏,王京晶

(1.北京师范大学水科学研究院 城市水循环与海绵城市技术北京市重点实验室,北京 100875；2.中国水利水电科学研究院水资源研究所,北京 100038；3.东北大学资源与土木工程学院,沈阳 110819)

近年来，我国经济社会快速发展，城市面积不断扩大，城市人口持续增长，城市水问题随之而来。城市“看海”层出不穷，逢雨必涝逐渐演变为我国很多大中城市的痼疾。气候变化与城市化对城市水文循环规律产生了深远的影响[1]，“城市雨岛”与“城市热岛”效应被广泛关注，城市内涝已成为危害居民财产安全的重要问题[2-5]。城市化使下垫面对降雨的响应机制发生改变，不透水面积增多，植被覆盖显著减少，径流量增加[6-7]。

城市雨洪模拟方法主要包括水文学方法、水动力学方法以及水文水动力结合的方法[8-9]。自然情况下，城市中的降雨经过初期损失后形成净雨，再经过坡面汇流进入城市管网中，最终由管网系统排出。在这一过程中，水流在城市地表的产流、汇流以及在管网中的汇流过程极为重要，是研究城市洪涝过程的重要工作。国内外相关研究人员[10-12]已针对城市雨洪模拟开展了大量研究。对于城市降雨径流的计算，我国自主研发的雨洪模型较少，主要集中在对径流量的计算上。岑国平[13]通过对城市雨水的地表产流、地表汇流、管网汇流过程进行研究，建立了城市雨水径流计算模型。周玉文等[14]将径流分为地表径流和管网径流两个阶段，构建了城市雨水径流模型。目前应用广泛的城市雨洪模拟软件包括美国环境保护署开发的SWMM(storm water management model)[15]、丹麦DHI开发的MIKE URBAN[16]以及英国Wallingford开发的InfoWorks ICM[17]。相比于其他模型软件，SWMM由于其开源的特性，被广大从事科学研究的人员应用在城市雨洪模拟中。石小芳等[18]基于SWMM对宁波地区构建了台风和非台风暴雨情景内涝响应模型，对比分析了两种不同暴雨情景下内涝的特征及差异。戎贵文等[19]基于SWMM中的低影响开发(low impact development,LID)模块以淮南某一工业园区为研究对象，分析了多种LID组合措施对水质水量的影响。目前，虽然关于SWMM的应用研究已较为丰富，但对于城市社区尺度下管网排水全过程的分析尚待进一步完善。鉴于SWMM开源的特点，本文基于实测场次降雨水位数据，采用优化算法对模型参数进行自动率定，并对各水文参数进行局部敏感性分析。在此基础上，选取不同重现期与不同降雨历时的组合工况对该管网排水系统进行计算。通过数据准备、模型构建、参数自动率定及敏感性分析、组合情景模拟及管网排水分析等主要步骤，以我国沿海地区福州市晋安区某典型排水小区为例，提出一套较为完整的城市排水内涝分析体系。

1 研究区数据

福建省会福州是典型的沿海易涝城市，位于闽江下游地区，属于亚热带季风气候。近年来，福州频繁受台风暴雨影响，强降雨天气严重影响人们的日常生活。如：2005年的“龙王”台风对福州市造成了极大破坏，城区主要交通道路几乎全部被淹;2016年的“鲇鱼”台风登陆福州时，12 h降雨量达到195 mm，经济损失14.2亿元[20-22]。选择福州市晋安区某典型居民区为研究区域，小区西面为茶园路，北面为晋安河支流，东面和南面以居民区街道与附近其他居民区相隔开，总面积约11.48 hm2。小区中有社区、学校、广场等典型居民区建筑设施。建模时，将房屋、广场、道路等概化为不透水面，将绿地等概化为透水面。图1(a)为该居民区位置示意图。利用SWMM对其排水系统进行评估，使用数据主要包括小区排水管网设施、土地类型以及小区地形。研究小区建模数据包括小区内的管网数据、地形数据和土地类型数据。管网数据包括检查井、管道、排口3个组成部分，其中：检查井数据包括检查井的位置、井底高程、井深；管道数据包括各管段的位置、形状、尺寸；排口信息包括排口位置等。

图1 研究区及SWMM概化图

本文使用2 m分辨率DEM数据计算子汇水区平均坡度，管网数据及地形数据来自于福州市城区水系联排联调中心，土地类型数据通过目视解译得到。概化的小区SWMM见图1，共计排口6个，检查井78个，管段78根。图1(b)为SWMM的概化示意图，本文使用的部分建模数据见表1。

表1 SWMM需要的基础管网数据

2 主要方法

2.1 SWMM

SWMM是一个分布式水文模型，将子汇水区作为基本水文响应单元，产汇流过程在每个基本单元上进行计算。根据不同的城市地表特性，每个基本单元被概化为透水区和不透水区两部分。在不透水区中，根据地表是否能够洼蓄划分为有洼蓄不透水区和无洼蓄不透水区两部分。基于研究区地形数据，利用ArcGIS表面分析计算百分比坡度，通过分区统计可得各子汇水区的平均坡度为2.09%。该模型[23]提供了下渗、坡面汇流及管网汇流等主要的水文水动力计算。

SWMM的下渗模块提供了Horton模型、Green-Ampt、Curve Number等不同的下渗模型，本文选择广泛使用的Horton模型进行计算。Horton模型可以较好地描述下渗率随降雨动态变化过程的规律，其计算公式为

ft=fc+(f0-fc)e-kt

(1)

式中：ft为土壤t时刻下渗率，mm/h；f0为初期下渗率，mm/h；fc为稳定下渗率，mm/h；t为时间，h；k为衰减指数，1/h。

在计算坡面汇流时，SWMM将每一个子汇水区概化为一个非线性水库，将最大洼地蓄水量作为水库的容量，根据水量平衡方程计算每一个水库中的水深，通过曼宁公式计算得到地表出流量为

(2)

式中：Q为出流量，m3/s；W为子流域宽度，m；S为平均坡度；n为地表曼宁系数;d为水深，m;dp为洼蓄深度，m。

城市雨洪过程中，经下渗损失后形成的净雨由坡面汇流进入管网系统。在管网汇流阶段，SWMM提供了恒定流、运动波、动力波3种计算方式。其中：恒定流假设管网中任意时刻水流运动要素保持不变，是对实际水流运动最为简化的处理方式；运动波通过联立求解简化的连续方程和动量方程计算水量，但是其无法有效模拟复杂逆坡、回水、环状管网等复杂的实际情形；动力波通过求解完全的圣维南方程组，可以对复杂流态进行模拟。因此，本文采用动力波对管网水流进行模拟。

(3)

(4)

式中：Q为流量，m3/s；H为水深，m；A为过水断面面积，m2；g为重力加速度，9.8 m/s2；Sf为摩阻比降；t为时间，s；x为距离，m。

2.2 遗传算法

遗传算法(genetic algorithm，GA)是一种通过模拟自然选择和进化过程来搜索最优解集的算法，常被使用在最优化问题的研究中。由于SWMM开源的特性，可以在遗传算法优化参数过程中，将SWMM的模拟值与实测数据计算得到的评价指标作为遗传算法种群个体中的适应度函数，进而完成遗传算法的更新迭代。遗传算法主要包括以下3个基本的遗传算子，分别为交叉操作、变异操作和选择操作。基于遗传算法优化SWMM参数的主要步骤见图2。

图2 遗传算法优化SWMM参数步骤

初始种群的初始化。SWMM需率定的参数构成一个解空间，设置进化代数计数器以及最大进化代数，并随机生成M个个体作为初始群体P(0)。

个体适应度计算。计算群体P(t)中各个个体的适应度。

将交叉算子作用于群体，交叉算子是遗传算法中起核心作用的算子。

将变异算子作用于群体。即是对群体中的个体串的某些基因座上的基因值作变动。群体P(t)经过选择、交叉、变异运算之后得到下一代群体P(t+1)。

计算目标函数。将更新得到的种群个体作为需要率定的模型参数，SWMM通过读取其输入文件(.inp)进行计算，(.inp)是一个结构化的文本格式，模型参数在文本中位于对应的模块下，通过Python语言对其进行参数的读取和写入。在参数替换为GA更新后的个体数值后，即产生新的(.inp)文件，即更新后的模型驱动数据，利用第三方库Pyswmm可以方便地调用模型计算引擎，以获取SWMM计算结果，提取目标点位水位或流量过程作为模拟值，通过模拟值与实测值计算目标函数。该步骤是通过遗传算法率定SWMM参数的核心。

选择操作。将选择算子作用于群体。选择的目的是把优化的个体直接遗传到下一代或通过配对交叉产生新的个体再遗传到下一代。选择操作是建立在群体中个体的适应度评估基础上的。

终止条件判断。在每轮迭代更新种群后，计算纳什效率系数或判断是否已满足迭代次数要求，如满足条件则停止遗传算法迭代过程，以算法进化过程中的最大适应度个体作为最优解输出，并终止循环。

2.3 Morris敏感性分析

本文选用Morris筛选法分析参数的敏感性[24]。Morris筛选法是从模型参数中选出某一个变量，在其取值范围内进行变动，使自变量以固定步长百分率改变，并以此驱动模型，从而得到不同xi对应的目标函数y的结果。最终敏感性判别因子取多个Morris系数的平均值，其计算公式为

(5)

式中：y*为改变参数后的模型输出；y为改变参数前的模型输出；Δxi为参数的变化。本文针对通过遗传算法率定的参数，选取一定范围改变参数值，并固定其他参数，以研究区主要排水口的洪峰流量为衡量指标，分析各参数的灵敏性。敏感性系数的计算公式为

(6)

式中：Y0为基准输出结果；Yi为参数第i次变化的输出；Pi为参数相对于基准输入的百分比变化量；n为参数的改变次数；S为参数的敏感性判别因子。当|S|≥1时，表明参数高度敏感；当0.2≤|S|<1时，表明参数中高等敏感；当0.05≤|S|<0.2时，表明参数中低等敏感；当|S|<0.05时，表明参数不敏感。

3 结果分析

3.1 参数优化及其敏感性

在构建研究小区SWMM的过程中，综合利用泰森多边形以及研究区的卫星影像图对其进行子流域划分。计算时每个子流域可以看作一个集总式水文模型，且包括下渗、地表汇流以及管网汇流3个主要的物理过程。因此，SWMM降雨径流模拟中主要有以下3个模块的参数，包括：子汇水区面积(hm2)、不透水百分比(%)、特征宽度(m)、平均坡度百分比(%)、不透水地表曼宁系数、透水地表曼宁系数、不透水地表洼地蓄水深度(mm)、透水地表洼地蓄水深度(mm)等子汇水区模块参数；最大入渗速率(mm/h)、最小入渗速率(mm/h)、衰减指数(1/h)等下渗模块参数；糙率等管道汇流模块参数。其中:子汇水区面积(hm2)、特征宽度(m)等参数由实际地形数据提取得到，不需要进行人为率定;而其他参数如糙率、最大入渗速率(mm/h)、最小入渗速率(mm/h)等虽然具有明确的物理意义，但是一般需要通过实测数据与模拟数据的对比来进行率定。由于其物理意义明确，这类参数通常具有一定的取值范围，而其中一些参数对模型模拟结果影响比较大，称之为敏感参数。准确率定模型参数，使模型能够更好地体现研究区实际特征，是建模过程中十分重要的步骤。在实际工作中，往往有大量的监测数据，手动率定往往带有极大的主观性，且工作量很大。与手动调参相比，遗传算法能够实现模型参数的自动寻优，为模型率定工作提供了便利。本文在遗传算法中，设置种群参数为30，迭代次数为200，其余超参数的突变概率设置为0.1，交叉概率为0.5，适应度函数使用纳什效率系数(Nash-Sutcliffe coefficient of efficiency，ENS)，其计算表达式为

(7)

本文通过参考文献中给出的模型参数范围，以汇水区及管道参数的上、下阈值作为遗传算法种群个体的上下边界。参考文献[25]与文献[26]，分别设置SWMM中子汇水区模块、下渗模块、管道模块中的参数，见表2。经过200次迭代，遗传算法计算得到的参数值已趋于收敛，最终得到的参数值如下所述。子汇水区模块参数中，不透水面曼宁系数为0.022，透水面曼宁系数为0.226，不透水区洼地蓄水深度为0.659 mm，透水区洼地蓄水深度为5.998 mm；下渗模块参数中，最大下渗率为83.62 mm/h，最小下渗率为1.534 mm/h，衰减系数为3.502，干燥时间为5 d；管道模块参数中，糙率为0.01。

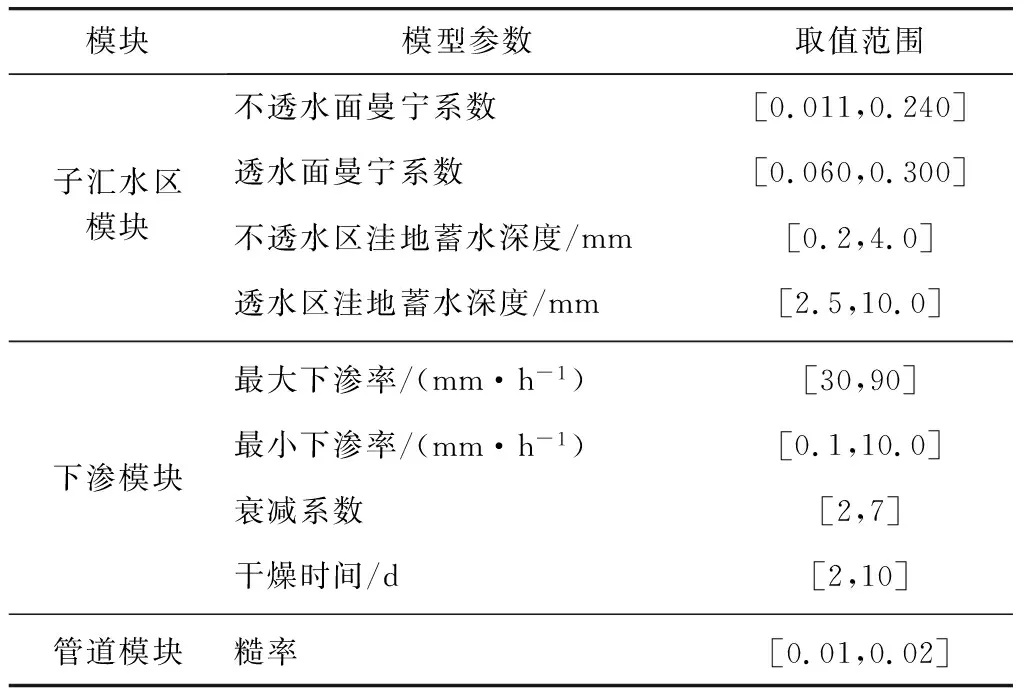
表2 SWMM关键参数的取值范围

率定期选取20180531场次降雨，该场次总降雨量为43.8 mm，降雨历时为200 min，计算得到纳什效率系数为0.82。实测最大水位为4.64 m，模型计算得到的水位为4.66 m。实测峰现时间为当日20：40，模型计算得到峰现时间为20：35。将模型率定得到的参数代入SWMM，并用验证场次的降雨数据驱动模型，将模拟结果与验证场次的实测数据进行比较。验证期选取20180620场次降雨，该场次总降雨量为53.1 mm，降雨历时为240 min，计算得到纳什效率系数为0.81。实测最大水位为4.750 m，模型计算得到的水位为4.758 m。实测峰现时间为当日18：30，模型计算得到峰现时间为18：25。因此，模型模拟的效果较好，可以用于实际洪涝情景计算。两次峰值的模拟水位和实测水位误差均在2%以内，模型的拟合度较高。率定参数后的SWMM在两场降雨实测水位与模拟水位的对比见图3。

图3 模拟水位与实测水位

由于小区实测资料比较缺乏，无法使用更多的场次降水资料进行模型率定和验证。较少的实测数据较易导致模型的适用性降低。因此，为进一步深化对模型参数的认识，有必要对模型主要参数的灵敏性进行一定的分析，找到敏感性强的参数，在模型的后续应用中重点率定这些参数。对于不敏感的参数，结合参数的物理意义及其取值区间进行适当调整。利用修正的Morris法，将率定后的参数作为基准参数值。为分析主要参数的灵敏性，在原参数基础上设置-30%、-20%、-10%、10%、20%、30%的变动，驱动模型计算得到多组输出结果。选择排水口的洪峰流量和小区平均径流系数为衡量指标，分析和讨论各参数的敏感性。

图4为采用Morris筛选法得到的洪峰流量对模型参数敏感性系数S分布，在计算过程中发现，下渗模块的参数干燥时间在变动中对结果的影响为0，这里不在图中作出。从图4可以看出，随着重现期的变化，各参数敏感性有所变化，其中：在重现期为1 a时，各参数敏感性系数分布较为接近，均位于[0.05,0.20)内，属于中等敏感参数；在重现期为20 a 时，最大下渗率位于[0.2,1.0)内，属于敏感参数，其他参数仍为中等敏感，但判别因子S有所增大；在重现期为50 a时，衰减系数与最小下渗率位于[0.2,1.0)内，属于敏感参数，其他参数为中等敏感。在该小区模型中，最大下渗率、最小下渗率以及衰减系数的敏感性系数随雨强的变化更为明显。

图4 Morris筛选法洪峰流量对参数的敏感性系数S分布

3.2 SWMM情景模拟

以3种设计降雨驱动模型，设计雨型来自福建省《城市及部分县城暴雨强度公式》[27]，共设置16种降雨方案。其中：设置4种降雨重现期，分别为1 a一遇、10 a一遇、20 a一遇、50 a一遇；同时设置4套降雨历时方案，分别为2、6、12、24 h。所有设计暴雨方案见表3。20 a一遇的3种降雨历时下的设计降雨过程线见图5。

表3 设计降雨方案

图5 20 a一遇的3种设计降雨过程线

设置4种降雨重现期以及4种降雨历时，通过SWMM计算得到在16种情景下小区排口的洪峰流量。小区内共有2个主要的排水管网系统，因此分别统计了2个排口处的流量过程线，见图6。图6中的C17为连接排口A的管道，C74为连接排口B的管道，分别用以统计模型计算的过流量。

通过计算可知，模型较为准确地模拟了小区的降雨径流过程。降雨历时为2 h时:当重现期为1 a时，排口A的洪峰流量为0.39 m3/s，峰现时间为1:00；当重现期为10 a时，排口A的洪峰流量为0.59 m3/s，峰现时间为0:55；当重现期为20 a，排口A的洪峰流量为0.67 m3/s,峰现时间为0:55;当重现期为50 a时，排口A的洪峰流量为0.75 m3/s,峰现时间为0:55。对于排口B以及其他重现期的降雨规律类似，随着降雨重现期的增加，该小区的洪峰流量逐渐增加，峰现时间较为接近。从图6还可以看出：当降雨重现期为20 a时，2 h降雨历时下排口B的洪峰流量为0.32 m3/s，峰现时间为0：55，而此时的降雨峰值出现时间为0：50；6 h降雨历时下排口B的洪峰流量为0.32 m3/s，峰现时间为2：30，而此时的降雨峰值出现时间为2：25；12 h降雨历时下排口B的洪峰流量为0.34 m3/s，峰现时间为4：55，而此时的降雨峰值出现时间为4：50；24 h降雨历时下排口B的洪峰流量为0.32 m3/s，峰现时间为9：40，而此时的降雨峰值出现时间为9：35。可以看到在不同的降雨历时下，小区排口峰值流量比较接近，而峰现时间直接受雨型的影响，一般出现在降雨峰值后的5 min。为进一步分析小区管网排水特征，统计各情景方案下小区排口的洪峰流量，见表4。相比于降雨历时，小区洪峰流量受降雨重现期或雨强的影响较大。

表4 不同内涝情景下的洪峰流量(排口B)

图6 不同情景下排口流量过程模拟

3.3 管网排水能力分析

为进一步分析小区管网排水特征，在4种降雨重现期与4种降雨历时的组合下驱动SWMM，并将模型计算时间统一设置为48 h，统计各情景方案下管网排水特征，见表5。在不同重现期下，均有部分节点和管道发生超载。节点超载个数和管道超载个数达52个以上。对于同一降雨历时的降雨，随着降雨重现期的增大，由于降雨强度变大，同一时间内城市下垫面收集的雨水更多，汇入排水管网的水量更大，这使得节点超载数、节点溢流数、满流管道数以及满管时间均呈现增加的趋势。但节点平均超载时长却呈现减少的趋势，是由于在降雨重现期增大导致超载的节点随之增多所致。当降雨重现期不变，降雨历时变大时，节点平均超载时长、节点超载数、满流管道数基本保持不变，而节点溢流数减少，满管时间增加。其中，在更短的降雨历时下，同一重现期降雨在时程上的分配更为密集，当管道排水能力不足时，水从管道两侧进入检查井，此时更容易造成检查井溢流，实际中对于短历时强降雨要引起足够重视。总的来说，各项指标受降雨重现期的影响较大，而节点超载数、满流管道数受降雨历时影响相对较小。

表5 不同内涝情景下管网排水特征统计

4 结 论

以福州市某典型居民小区为例，基于实测的管道液位数据，利用遗传算法对SWMM参数进行优化率定，并利用Morris法对影响产汇流计算的主要参数敏感性进行了分析。在此基础上，利用不同重现期的降雨驱动模型，比较分析各种情景下小区排水管网的排水能力。主要结论如下：

基于遗传算法率定研究区SWMM参数，20180531场次降雨计算得到纳什效率系数为0.82；实测最大水位为4.64 m，模型计算得到的水位为4.66 m；实测峰现时间为当日20：40，模型计算得到峰现时间为20：35。20180620场次降雨计算得到纳什效率系数为0.81；实测最大水位为4.750 m，模型计算得到的水位为4.758 m；实测峰现时间为当日18：30，模型计算得到峰现时间为18：25。基于Morris筛选法进行SWMM参数敏感性分析，得到洪峰流量对模型参数敏感性系数S分布图。结果显示，降雨重现期较小时，参数敏感性系数分布相对均匀。随着降雨重现期增大，参数敏感性分布相对集中。衰减系数、最大下渗率、最小下渗率以及管道曼宁系数比其他参数更为敏感。

对研究小区进行管网排水计算，得到不同降雨情景下的洪峰流量、节点平均超载时长、节点超载数、节点溢流数、满流管道数、满管时间等指标。结果表明，在降雨历时相同时，随着降雨重现期的增加，该小区的洪峰流量逐渐增加，峰现时间较为接近。在不同的降雨历时下，小区排口峰值流量比较接近，而峰现时间直接受雨锋的影响，一般出现在降雨峰值后的5 min。在降雨历时增加时，满管时间相应增加。各项指标受降雨重现期的影响较大，其中，节点超载数、满流管道数受降雨历时影响相对较小。

本文在城市社区尺度下完成排水模型构建、参数率定及敏感性分析、组合工况模拟及排水能力量化分析等工作，较为完整地分析了城市排水内涝情势，对相关防洪排涝工作有一定的借鉴意义。论文工作本身也存在以下不足：实测数据的缺乏使本文仅使用2场实测雨洪过程进行参数的率定和验证，使模型参数在其他场次降雨中的泛化能力有所欠缺，未来应搜集更多的实测资料，不断地对模型进行优化，增加模型的鲁棒性和泛化能力。此外，更多的实测资料也有利于进一步对遗传算法的超参数进行校核；本文仅对社区尺度洪涝过程中地表产流、地表汇流及管网汇流3个过程做了模拟，并未涉及河网汇流及地表漫流等重要过程，如直接导致城市内涝节点的溢水过程。在后续工作中需要将SWMM与其他模型工具相结合，综合利用水文与水动力学方法，模拟城市尺度洪涝全过程。