山区公路边坡工程智能分析与设计研究进展
陈昌富 李伟 张嘉睿 廖佳卉 吕晓玺

摘要:隨着我国高速公路建设不断向中西部山区延伸,形成了大量高陡边坡,打破了原有山体的地质和生态平衡,极易诱发滑坡、坍塌、泥石流等地质灾害,严重威胁人民的生命和财产安全.因此,山区高陡边坡的稳定性分析、设计、处治、监测等问题一直是岩土工程中研究的热点和难点.由于岩土高陡边坡具有高不确定性、强非线性和动态演化的特征,基于经典理论的分析和计算方法对上述问题进行研究难以获得合理的解答,而人工智能技术方法具有处理非线性复杂系统的独特优势,现已成为解决公路边坡工程问题的有效手段.本文总结了最近10余年山区公路边坡工程中边坡稳定性智能分析计算与评价方法、边坡防护与加固智能设计计算方法、边坡智能监测技术、滑坡智能识别和预测、岩质边坡结构面智能识别以及岩士体参数智能反演等方面的主要研究进展,并简要说明了在山区公路边坡稳定性分析与加固设计、现场监测和滑坡预测等方面推进智能化建设的进一步发展方向.
关键词:边坡;人工智能;智能算法;机器学习;深度学习;神经网络;稳定性;边坡防护与加固;边坡监测与预测
中图分类号:U418.5文献标志码:A
State-of-the-Art of Intelligent Analysis and Design in Slope Engineering of Highways in Mountainous Areas
CHEN Changfu1,2,LI Wei1,2,ZHANG Jiarui1,2,LIAO Jiahui1,2,LU Xiaoxi1,2
(1. Key Laboratory of Building Safety and Energy Efficiency of Ministry of Education (Hunan University),Changsha 410082,China;2. College of Civil Engineering,Hunan University,Changsha 410082,China)
Abstract:As the construction of highways extend to the mountainous areas in the central and western regions in China,a large number of high-steep slopes have been generated. The construction process not only broke the geological and ecological balance of the original mountains,but also easily to induce geological disasters such as land - slides,collapses and debris flows,which seriously threaten people's lives and property safety. Therefore,some problems of high-steep slopes in mountainous areas have always been the key and difficult points in geotechnical engineering,including stability analysis,design,treatment and monitoring. However,due to the characteristics of high uncertainty,strong nonlinearity and dynamic evolution of high-steep slopes,it is difficult to obtain reasonable answers to the above problems based on analysis and calculation methods of classical theory. Artificial intelligencetechnology has the unique advantage of dealing with nonlinear complex systems,and it has become an effective means to solve slope engineering problems in highway. Therefore,this paper summarizes the main research progress in several fields of slope engineering of highway in mountainous areas in the past 10 years,including intelligent analysis calculation and evaluation method of slope stability,calculation method for intelligent design of slope protection and reinforcement,intelligent monitoring technology of slope,intelligent identification and prediction of landslides,intelligent inversion of rock and soil parameters,intelligent identification of rock slope structural planes,and so on. Furthermore,the further development direction of intelligent construction of slope engineering in highway is briefly explained in the fields of slope stability analysis and reinforcement design,on-site monitoring and landslide prediction.
Key words:slope;artificial intelligence;intelligent algorithm;machine learning;deep learning;neural network;stability;protection and reinforcement of slope;monitoring and prediction of slope
随着我国高速公路建设不断向主要由丘陵或山地组成的中西部山区延伸,不可避免地需要进行大填大挖,从而必然形成大量的高陡边坡.高陡边坡的开挖施工不仅打破了地表原有的地质和生态平衡,对公路沿线周边的地质和生态环境产生重要影响,而且在强降雨或地震荷载作用下,高陡边坡极易诱发滑坡、坍塌、泥石流等地质灾害,严重威胁人民的生命和财产安全.因此,国内外学者为确保山区公路边坡安全,在边坡稳定性分析、防护与加固设计、现场监测和滑坡预测等方面做了大量的研究,并取得了丰硕的成果.
边坡稳定性分析的关键是边坡中最危险滑动面的搜索.然而,山区公路边坡因受到复杂地形地质条件和各种工程等因素的综合影响,具有高度不确定性、强非线性和动态演化的特征,这导致在最危险滑动面搜索过程中经常面临安全系数计算公式为隐函数、目标函数为高维且具有多极值点的非凸函数等突出问题,采用经典的分析计算方法难以求解. 近年来,随着人工智能(AI)技术的快速发展,智能算法和机器学习模型被广泛应用到边坡工程的稳定性分析中,建立了大量收敛能力强、计算精度高、搜索速度快的全局优化搜索方法[1-6],可有效解决复杂边坡的稳定性分析和最危险滑动面搜索问题.
对于欠稳定或已失稳边坡(滑坡),为保证工程安全,必须对其进行加固处理.在工程中,由于边坡处治涉及的因素众多、建模困难、计算复杂,如何合理选择边坡处治加固形式并对其进行优化设计,以获得经济合理、技术可靠的边坡加固设计方案,一直是边坡处治的重点和难点.为此,一些学者采用智能算法[7]、机器学习[8]、模糊计算[9]、自适应神经模糊推理系统[10]等人工智能方法,对边坡处治进行智能设计,取得了良好的效果.
滑坡和泥石流是山区公路的高发地质灾害,防灾减灾任务十分艰巨.其中,滑坡的精准监测和预测预警是边坡防灾减灾的关键环节.随着航空航天和光学遥感技术的发展,新型的边坡监测技术不断涌现,并逐渐向高精度、自动化、智能化、远程化的方向发展[11].同时,监测内容也日益丰富,除最常见的位移外,还拓展到裂缝、地下水、气象等多项监测指标[12].智能监测虽然可获得大量多维度的、非线性的、高分辨率的多源监测数据,但也使多源数据的融合和关键信息的识别和提取成为技术难点.而机器学习方法可以在复杂的数据中建立目标对象与属性特征之间的关系框架;智能算法可以优化模型参数,提高搜索能力.因此,它们被广泛应用于滑坡的智能识别与预测预警、岩体结构面的智能辨识等研究中,并且成效显著.
为展示国内外山区公路边坡智能分析和设计方面的最近研究进展,本文在查阅大量文献的基础上,重点对最近10余年来公路边坡稳定性智能分析与设计计算方法、边坡处治智能设计计算方法、边坡智能化监测技术、滑坡的智能预测、岩土体参数智能反演以及岩质边坡结构面智能识别等方面的研究进展进行较系统的总结,并就人工智能用于解决山区公路复杂边坡稳定性分析与加固设计、现场监测与滑坡预测等问题的发展方向给予展望.
1山区公路边坡智能分析与设计计算方法研究进展
1.1概述
边坡稳定性分析是公路边坡设计和施工的理论基础.目前,常用的边坡稳定性分析方法众多,其分类如表1所示.本节将系统地回顾人工智能方法应用于边坡的确定性分析和非确定性(可靠性)分析,以及工程边坡优化设计的最新研究进展.
1.2山区公路边坡稳定性智能分析方法
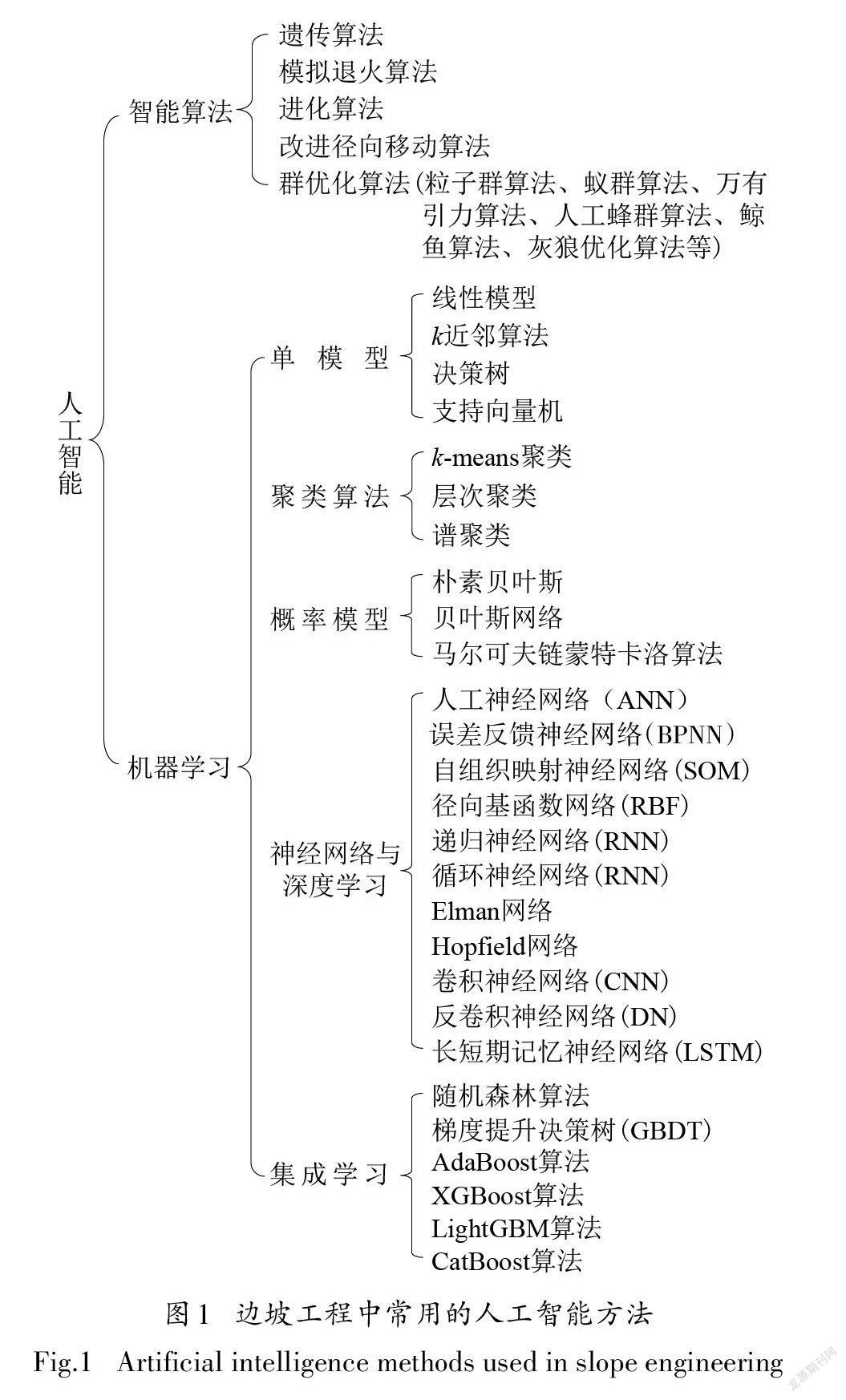
边坡稳定性分析的实质是寻找一条使边坡的安全系数最小的滑动路径,这条路径可称为最危险滑动面(亦称临界滑动面).由于边坡系统的复杂性,临界滑动面的目标函数通常是一个复杂且不可微的多峰函数,采用传统的搜索方法极易陷入局部最优解.近年来,诸多学者基于人工智能算法和机器学习,提出了众多收敛能力强、高效、稳定的全局优化分析方法来定位边坡临界滑动面和计算边坡的稳定性.在智能算法方面,有遗传算法[1]、模拟退火算法[2]、进化算法[3]、改进径向移动算法[4]、群优化算法(粒子群算法[15]、蚁群算法[14]、万有引力算法[15]、人工蜂群算法[16]、鲸鱼算法[17]、灰狼优化算法[18])等;在机器学习方面,有单模型(如支持向量机[5])、聚类算法、概率模型、神经网络与深度学习[19]、集成学习[20]等,详细分类如图1所示.上述人工智能模型均可独立用于解决边坡稳定性问题,但也各有不完善之处,因此诸多学者通过对它们进行不同方式的组合或融合,提出了一些适应性更强的改进算法.
1.2.1基于遗传算法(GA)的边坡稳定性分析
针对传统遗传算法(GA)的局部寻优能力不足,易因选择压力过大而产生早熟收敛的问题[21],Zhu 和Chen[22]将局部禁忌搜索策略植入遗传算法的重组和循环中,提高了局部寻优速度.Cen等[23]将遗传算法和模拟退火算法相结合,对生成的每个子滑面采用模拟退火操作,实现了快速收敛.Zhou等[24]通过在上一代最优解区域附近生成新种群,并与初始种群遗传重组的方式扩大种群多样性,加快了收敛速度.Xu等[25]结合改进的量子遗传算法和随机森林回归方法,通过动态调整策略控制种群的更新和演化方向得到全局最优解,有效地避免了过早收敛.
1.2.2基于模拟退火算法(SA)的边坡稳定性分析
1983年,Kirkpatrick等[26]将热力学中的退火思想引入组合优化领域,提出了一种求解大规模组合优化问题的有效近似算法——模拟退火算法(SA).然而,由于在模拟退火过程中很难保证退火充分,导致在解的搜索过程中极易陷入局部最优解,全局搜索能力较差.Cheng[2]提出了一种动态边界模拟退火技术,可准确且快速地确定圆弧和非圆弧滑动面的最小安全系数.刘华强等[27]通过增加算法的記忆功能和联合搜索能力,给出了一套边坡稳定分析的非圆弧滑动面搜索方法.李亮等[28]引入禁忌搜索技术,避免了对退火中新解的重复、迂回搜索,形成了全局寻优能力极强的禁忌模拟退火复合形法.
1.2.3基于粒子群算法(PSO)的边坡稳定性分析
粒子群算法(PSO)[13]是采用速度-位置搜索模型,各粒子代表解空间中的一个候选解,通过定义适应值函数来评价各粒子的优劣程度,该算法的适应性和兼容性较强,但也存在计算时比较依赖惯性因子的取值、易陷入局部最优解、计算量大等缺点.李亮等[29]借鉴和声算法直接模拟群体的位置更新,通过对简化Janbu法的拓展,实现了对边坡三维临界滑动面的快速搜索.徐飞等[30]结合投影寻踪算法、粒子群优化算法和逻辑斯谛曲线函数,建立了边坡稳定性评价的粒子群优化投影寻踪模型(PSO-PP).杨善统等[31]通过变异操作增强了粒子群跳出局部最优解的能力,并用二次序列规划加速局部搜索,大大提高了粒子群算法获得全局最优的能力.
1.2.4基于蚁群算法(ACO)的边坡稳定性分析
蚁群算法(ACO)[14]具有开放性、鲁棒性、并行性和全局收敛性等优点,但也存在早熟收敛、收敛速度慢和求解质量差等问题.为了克服原有算法的缺点,陈昌富等[32]引入混沌扰动算子,改变了蚂蚁的选择机制,增加解的多样性,提高了全局寻优能力.石露等[33]对蚁群算法的结构和蚂蚁转移概率计算方式进行了改进,并与遗传算法结合,克服了蚁群算法初期因信息素匮乏导致计算速度慢的不足.Gao[34]引入奖惩策略,增加较优路径与普通路径的信息素差异,加快了收敛速度,也避免早熟收敛;他还基于蚂蚁正反向搜索相遇形成完整路径的原理,提出了一种相遇蚁群算法,提高了搜索效率和精度[35].Yang等[35]将MAX-MIN蚁群优化算法应用于稳定性分析的滑动面搜索上,提出一种基于数值流行法的数值模型,算例表明其具有较好的适用性.
1.2.5基于万有引力算法(GSA)的边坡稳定性分析
万有引力算法(GSA)是由Rashedi等人提出,利用万有引力定律和模拟物体间的相互作用,得到一种粒子群体智能优化算法.考虑到万有引力算法局部搜索能力不足,易出现最优值振荡发散的现象,Khajehzadeh等[15]采用自适应最大速度约束,提高了全局探索能力和收敛速度.Raihan等[37]将万有引力算法与顺序二次规划(SQP)相结合,提出了一种GSA-SQP优化算法.蒋建国等[38]通过限制粒子的速度和更改算法参数对万有引力算法进行改进,显著提高了算法中粒子的探索与开发能力.
1.2.6基于新型群优化算法的边坡稳定性分析
目前新的群优化算法层出不穷,而且不断被应用于边坡稳定性分析中.比如:Ma等[39]根据仿生学原理和海豚的捕食行为,基于领导者海豚群算法(LDHA)创建了边坡稳定性分析的非线性多目标优化模型,计算结果表明LDHA在计算精度和效率上明显优于其他算法.Li等[40]比较了8种新型优化算法[灰狼优化算法(GWO)、粒子群优化算法(PSO)、鲸鱼优化算法(WOA)、Salp群算法(SSA)、多元优化算法(MVO)、蚂蚁狮子优化算法(ALO)、布谷鸟搜索算法(CS)和平衡优化算法(EO)]确定边坡临界滑坡面的能力,结果表明,平衡优化算法在解的质量、收敛速率和鲁棒性方面优于其他算法.
1.2.7基于支持向量机(SVM)的边坡稳定性分析
支持向量机(SVM)是一种支持小样本的机器学习,以结构风险最小化为准则,缩小模型泛化误差,提高泛化能力,但在求解大规模样本数据时,具有效率低、鲁棒性差等问题[5].考虑到SVM的准确性与核函数和惩罚参数的取值相关,陈光耀等[41]基于正态云模型改进果蝇算法,并用于求解SVM分类模型的最优参数组合,提出了一种有效、可行的边坡稳定性评价方法.Suykens等[42]通过在目标函数中增加误差平方和项,将原有的不等式约束求解过程变成等式方程求解,节省计算时间,提出了最小二乘支持向量机(LSSVM)方法,加快了求解速度.Xue[43]采用PSO算法改进LSSVM方法,在收敛速度和精度上较经典的遗传算法和粒子群算法更优.Zeng等[44]采用引力搜索算法和鲸鱼优化算法分别讨论了LSSVM方法的正确控制參数.Cai等[45]采用混沌遗传算法对LSSVM参数进行优化,提高了并行计算和全局优化搜索的能力.Li等[46]提出了基于量子化粒子群(QPSO)的LSSVM算法,相比于PSO-LSSVM和LSSVM算法,具有更快的搜索速度和最佳的收敛性能,更适合于边坡稳定性分析.
1.2.8基于人工神经网络(ANN)的边坡稳定性分析
人工神经网络(ANN)是一种模拟人脑神经网络结构和功能的计算模型,通常由一层或多层互连的神经元或节点组成.人工神经网络能够充分考虑各因素间的非线性关系,实现对任意函数的逼近,已经得到了较为广泛的应用[19].但是,人工神经网络模型在训练中易出现信息重叠和过拟合现象,从而导致泛化能力差等问题.陈昌富和杨宇[47]采用基于人工神经网络结构构建的T-S型模糊推理系统,利用混合遗传算法训练该模型,避免了隶属函数难以确定的问题,提高了搜索效率.Gordan等[48]借助粒子群算法(PSO)确定ANN的权重和偏差问题,提出一种PSO-ANN模型来预测边坡的稳定安全系数,提高了搜索精度.Das等[49]分别采用差分进化神经网络(DENN)、贝叶斯正则化法神经网络(BRNN)和Levenberg-Marquardt神经网络(LMNN)模型计算边坡的安全系数,对比计算结果发现,DENN模型计算精度更高.Khajehzadeh等[50]提出了一种ANN模型与自适应正余弦算法结合的智能分析方法,并用于评估和预测均质边坡在静态和动态载荷下的安全系数.Foong和Moayedi[51]使用平衡优化和涡流搜索算法优化多层感知器神经网络模型来预测单层土坡的安全系数.
误差反馈神经网络(BPNN)[52]是一种改进的人工神经网络模型,在其输入层和输出层之间至少有一个隐含层,每个互连都分配有一个关联权重,具有向前和向后传递两个过程,因而能够将输出层不准确的结果向前传递,通过更新连接权重使误差最小化,提高预测精度.胡军等[53]结合协调粒子群算法和BP神经网络,建立了边坡稳定性与各影响因素之间复杂的非线性关系,避免了BP神经网络易陷入局部最优的问题.考虑到卷积神经网络(CNN)在图像分析方面具有更好的表现,Hsiao等[54]将CNN模型与ANN模型用于随机场边坡的安全系数和临界滑动面搜索,以平均绝对误差来判断性能差异,结果表明,CNN模型在复杂边坡情况下精确度比ANN模型更高,同时缩短了运算时间.
1.2.9基于集成学习的边坡稳定性分析
集成学习[20]通过构建并结合多个弱学习器,形成基于个体学习的强学习器,它可以获得更准确的预测结果,具有更好的泛化性能和更广泛的应用. Qi和Tang[55]采用自适应增强决策树(ABDT)、二次判别分析、支持向量机(SVM)、人工神经网络(ANN)、高斯过程回归(GPR)和k-最近邻(KNN)作为弱学习器,通过加权多数投票法组合构建了集成学习分类器.另外,他们也采用萤火虫算法调整超参数,并验证和讨论了6种综合方法[Logistic回归、随机森林(RF)、决策树、梯度提升机(GBM)、多层感知器神经网络和支持向量机(SVM)]在边坡稳定性预测中的可行性,结果表明,集成学习方法大大提高了边坡稳定性预测性能[56].Sun等[57]提出了贝叶斯优化的集成学习算法,对4种回归算法的超参数进行优化,提高了边坡安全系数的预测精度.
1.2.10基于其他机器学习方法的边坡稳定性分析
不同的机器学习方法对同一类型的数据有不同的敏感度,同一类别的数据在不同方法下的分类精度也会有所不同,每个分类方法都有其独特性和局限性.因此,Lin等[58]基于349个边坡案例的数据集,评价了11种用于边坡稳定性评价的机器学习模型在不同输入参数组合下预测边坡安全系数的能力,通过数理统计分析发现支持向量机(SVM)、梯度提升回归(GBR)和装袋(Bagging)方法是相对较好的回归方法.Mahmoodzadeh等[59]基于高斯过程回归(GPR)、支持向量回归(SVR)、决策树(DT)、长短期记忆(LSTM)神经网络、卷积神经网络(CNN)和k-最近邻(KNN)模型分析327个案例边坡的稳定性,并与数值分析计算结果对比发现,GPR模型的预测更加准确.Karir等[60]基于支持向量回归(SVR)、人工神经网络(ANN)、随机森林(RF)、梯度提升(GB)和极端梯度提升(XGBoost)机器学习方法,建模并分析了边坡安全系数,与数值分析计算结果对比发现,RF、GB和XGB模型等基于树的算法具有出色的预测性能.Lin等[61]对比了4种监督学习算法[随机森林(RF)、万有引力算法(GSA)、支持向量机(SVM)和朴素贝叶斯算法]在边坡稳定性评价中的性能差异,其中万有引力算法可以获得最好的结果.目前的研究表明,还没有完善的机器学习方法能够对影响边坡稳定性的众多因素进行较全面和有效的分析,仍需要不断寻找精度更高、适用性强的机器学习方法来建立边坡稳定性评价模型,以获得更好的预测结果.
1.3山区公路边坡可靠度智能分析方法
自然边坡受长期风化、搬运、沉积、后沉积等地质作用的影响,土体强度参数往往具有随机性和不确定性.而常用的稳定性分析仅是在确定性参数条件下求解安全系数,不能有效地考虑实际荷载和边坡参数的随机性和不确定性,易使评价结果偏離实际.因此,国内外衍生出许多以概率表征的边坡可靠度分析方法,它们能够定量、客观地考虑这些不确定性因素对边坡稳定性的影响.而随着计算机和智能技术的蓬勃发展,引入人工智能技术的边坡可靠度分析研究也在日益增加.
边坡可靠度计算问题可以分为两类[62]:一类是极限状态方程是基本随机变量的显式功能函数;另一类是极限状态方程是基本随机变量的隐式功能函数,后者更为常见.当功能函数为不易求解的高度非线性的隐式函数时,一般采用代理模型法构建随机变量与功能函数之间的映射关系,如响应面法[63]、支持向量机(SVM)模型[64-65]等,并在此基础上应用各种可靠度计算方法来计算边坡可靠度指标.在代理模型的建立中运用人工智能技术,可大大提高计算效率,减少时间成本.Li等[64]基于支持向量机(SVM)代理模型构建功能函数,然后采用蒙特卡洛方法计算边坡可靠度指标,提出了一种基于SVM的边坡可靠度分析方法.Samui等[66]建立了相关向量机(RVM)在隐式功能函数的极限状态下的可靠性分析模型.苏永华等[67]基于Kriging模型建立了各向异性关联映射方法,再结合蒙特卡洛模拟和主动学习方法求解了边坡的失效概率.Kang等[68]提出了一种基于最小二乘向量机(LSSVM)和粒子群算法(PSO)结合的土质边坡系统失效概率评估可靠度方法.朱彬等[69]基于高斯过程回归算法构建代理模型,并用蒙特卡洛模拟求解边坡失稳概率,在保证计算精度的同时减少了对边坡稳定性分析程序的调用.张天龙等[70]提出了基于主动学习径向基函数的代理模型,加快了模型训练的收敛速度,然后结合蒙特卡洛模拟计算边坡的系统失稳概率.谢梦龙等[71]引入LASSO算法压缩数据系数,消除变量间的共线性问题,建立了边坡土体强度参数与安全系数的关系,与普通线性回归算法相比,其预测效果更有优势.
岩土体变异性包括地层变异性和岩土体参数的空间变异性[72].针对岩土体参数变异性对边坡稳定性分析的影响,许多学者引入随机场模拟不均匀参数的分布,并对稳定性进行了大量的探讨,提出了许多有效的可靠度评估方法[73].Li等[74]基于理论自相关函数,提出了一种考虑岩土体抗剪强度参数空间变异性的多响应面边坡可靠性分析方法.Qin等[75]考虑了土体参数的空间变异性对开挖边坡变形行为的影响,提出了一种基于随机有限元方法的贝叶斯更新框架,能够根据现场测量数据对边坡进行有效的安全性评估.杨智勇等[76]采用概率故障树模型构建了边坡多失效模式系统可靠度分析模型.姬建等[77]建立边坡土体随机场数字图像与功能函数值之间隐式关系的卷积神经网络(CNN)代理模型,显著提高了考虑随机场模拟的边坡可靠度分析计算效率.Zai等[78]提出了广义概率密度演化方法来评估边坡的系统可靠性,对于隐式函数和多参数变量的复杂斜坡分析具有很好的适应性.另外,在考虑岩土体地层软硬交替的变异性方面,Li等[79]根据钻孔资料结合耦合马尔可夫链模型模拟地层的不确定性,并对边坡进行稳定性分析,表明地层变异性对安全系数和失效概率不确定性有重要影响.Liu等基于现场有限的钻孔数据,采用一维马尔可夫链模型研究了地层边界不确定和土体参数空间变异性对边坡可靠性分析的影响.邓志平等[72]提出了同时考虑地层变异性和土体参数固有变异性的边坡可靠度分析方法,有效地反映了这两种土体变异性对边坡可靠度的影响.
对于呈线状分布的山区高速公路,因其线路长、场地勘察难度大,有关岩土参数的数据获取困难,导致用于可靠度分析的数据严重不足.为了解决数据样本量不足的问题,Yi等[81]在Kriging建模中引入粒子群算法以获得最优相关参数,通过对未监测点的插值和外推,可以增加初始数据,有效解决了小样本的参数不足.Xiao等[82]将改进的自适应遗传算法与时空Kriging插值法相结合来解决监测数据缺失的问题,其插值精度较传统时空Kriging和高斯过程回归(GPR)方法提高了约1倍.姬建等[83]运用概率密度权重法对边坡系统可靠度进行概率分析,实现了在低样本量下对高维、隐式极限状态方程的边坡可靠度的分析.另外,也有一些学者借助贝叶斯网络框架建立代理模型对样本数据进行合理的更新.比如,Yao等[84]提出了基于结构可靠度和贝叶斯更新的边坡可靠度更新方法,可以基于较少的样本数据,进行有效和准确的边坡可靠性分析;Contreras和Brown[85]基于贝叶斯方法构建了多维后验概率分布来推断边坡参数,并采用马尔科夫链蒙特卡洛方法进行了边坡可靠度分析;刘阳等[86]以贝叶斯网络为框架,结合模糊理论与支持向量机模型,提出了一种公路边坡地震失稳规模的评估方法,克服了样本量少引起网络参数误差过大的缺陷.
1.4山区公路边坡智能设计方法
在给定的工程场地(地质地形条件已知)和荷载条件下,山区公路边坡设计的关键是合理确定坡形和坡角.但由于影响边坡稳定性的地层物理力学参数和工程荷载等因素通常具有随机性、模糊性及离散性,故边坡的设计是一个复杂的非线性问题[87].在边坡坡角的智能设计中,张志军等[88]根据边坡的岩土力学参数及边坡高度,采用人工神经网络(ANN)方法和自适应神经模糊推理系统(ANFIS)方法,在满足安全系数要求下对圆弧破坏边坡的边坡角反演设计,结果发现ANFIS反演设计效果更好.徐冲等[87]采用基于组合核函数的高斯过程回归网络模型对边坡坡角进行智能设计,提高了预测精度和泛化能力,同时可较好地处理坡角设计中的非线性问题.Zhou等[89]将贝叶斯推理、概率运动学分析和立体投影应用于不连续性控制的岩石边坡不稳定性分析,计算出各开挖边坡潜在不稳定区块的破坏角. Yan等[90]结合运动学分析、贝叶斯估计和蒙特卡洛模拟,提出了一种确定边坡节理岩边坡的最大安全角的方法.Xie等[91]基于影响岩质边坡角的10个主要影响因素,构建了一种基于随机森林算法预测岩质边坡稳定坡角的新方法.
2山区公路边坡处治智能设计计算方法研究进展
2.1概述
山区公路修建时,不可避免地要对沿线边坡进行开挖、削坡和爆破等施工作业,会形成大量的深路堑和高路堤边坡.不仅破坏了沿线的生态景观,也容易引发水土流失、滑坡和坍塌等灾害,影响边坡的稳定性.为了保证公路安全、边坡稳定、生态平衡,应采取科学合理的边坡处治措施.而在边坡处治设计中往往涉及的因素众多,导致建模困难、计算复杂,因此,一些学者采用智能算法和机器学习模型方法对边坡处治进行智能设计,取得了良好的效果. 本节将对边坡不同防护与加固形式的智能设计研究进展进行较为详细的阐述.
2.2山区公路边坡植物防护智能分析计算方法
边坡防护主要有工程防护和植物防护两种形式,工程防护主要有喷护、锚杆挂网喷浆和砌块防护等,由于这些措施景观效果不好,已经不提倡使用,因此边坡防护的主要途径以植物防护为主[92].目前有关山区公路边坡防护智能分析计算方法的研究很少.Sari等[10]针对草、灌木和乔木防护的边坡,考虑根系加固作用,提出了一种高性能低误差的边坡稳定性ANFIS分析方法.随后,Safa等[93]考虑根系拉力作用,分别采用ANN、ANFIS和ABC-ANN(人工蜂群与神经网络混合)算法,对生态防护的黏性土质边坡的安全系数进行计算,结果发现,ANFIS算法具有更好的性能.此外,Liu等[94]建立了公路植物边坡稳定性评价指标体系,并运用粗糙集理论和层次分析法确定了边坡评价指标的权重,提出了一种有效且可靠的预测公路植物边坡防护质量的评价模型.Liu等[95]提出了一种结合遗传算法和BP神经网络回归的模型,结合气象和土壤湿度监测数据,可以对生态防护高边坡的水分进行合理预测.
2.3山区公路边坡加固智能分析计算方法
由于场地工程地质和工程条件的复杂性,边坡加固方式千差万别.目前,常用的公路边坡加固方法有加筋土坡、重力式或加筋土挡墙、土钉支护(土钉墙)、锚杆(索)挡墙、抗滑桩等.
加筋土坡因填方量少、施工期短、经济安全、抗震性能好等优点,在边坡工程中应用广泛,其相关的研究也较多.Ponterosso和Fox[7]提出了一种基于遗传算法的加筋土坡优化设计方法,并发现应用遗传算法可有效节省加固费用.Farshidfar等[96]采用遗传算法搜索加筋土坡的临界滑动面,提出了一种水平条分的加筋土边坡稳定性分析方法.Shinoda和Miyata[97]采用粒子群优化算法计算加筋土坡的安全系数,验证了案例边坡的稳定性,提高了计算精度和设计效率.Bahootoroody等[98]利用分层贝叶斯和马尔科夫链蒙特卡洛方法来评价土工布加筋土坡的失稳概率,提出了一种加固边坡可靠度分析计算方法.
挡土墻结构因抗滑能力强、布置灵活、施工方便、结构形式多样等优点而应用广泛.Gandomi等[99]采用加速粒子群优化、萤火虫算法和布谷鸟搜索等三种群体智能优化算法对悬臂式挡土墙的几何形状参数进行优化设计,发现在低成本和低耗材设计优化方面,布谷鸟搜索算法更精确.侯超群等[100]采用遗传算法确定地震作用下临水加筋土挡墙的临界滑动面,在满足其内部稳定条件下,得到了筋材拉力系数的优化设计结果.
土钉支护(土钉墙)的稳定性分析中多采用极限平衡法计算土钉支护结构稳定性安全系数.朱剑锋等[101]提出一种新型的自适应禁忌变异遗传搜索优化算法,该算法能获取土钉墙任意形状最危险滑动面及相应安全系数,快速确定边坡的稳定性.董建华和朱彦鹏[102]提出了地震作用下土钉支护边坡永久位移计算方法,其中采用遗传算法搜索土钉支护边坡的临界滑动面.惠趁意等[103]运用遗传算法对复合土钉支护结构边坡的最危险滑动面进行动态搜索,加快了设计速度.房光文等[104]为了切实反映土钉加固边坡的实际状态,考虑土体参数模糊随机性和边坡模糊过渡区间,提出了一种土钉加固边坡可靠度分析方法.
对于锚杆(索)挡墙的设计,可先假定锚杆长度为一定值,然后通过逐步试算安全系数确定最优设计方案.罗辉等[105]应用可靠度反分析法设计边坡锚杆,采用遗传算法求得目标可靠度下的锚杆优化设计长度.尹志凯等[106]基于改进的差分进化算法,对三维边坡锚固位置进行合理优化,优化后可有效节约锚杆数量.周苏华等[9]建立了预应力锚索加固顺层边坡的稳定性评价指标体系,提出了基于模糊层次分析法的边坡稳定性评定模型,并通过数值正交试验发现结构面强度和坡后角(即坡顶地面倾角)比边坡的高度和坡度对边坡的稳定性影响要显著. 谢全敏等[107]基于灰色关联度分析与模糊识别理论,建立了既有加固边坡锚杆结构健康状态诊断方法,其评估结果能够较全面、系统地反映既有锚杆加固边坡工程的整体健康状态.
抗滑桩是边坡支护中广泛采用的支挡结构形式.在抗滑桩设计时,一般是在指定的安全系数下计算出抗滑桩受到的下滑力,并据此设计确定桩距、桩径、桩长和配筋.唐晓松等[8]、杨波等[108]采用GASVM算法对埋入式和双排全长式抗滑桩的合理桩位和桩长进行了分析计算.梁冠亭等[109]基于改进M-P法建立了抗滑桩支护边坡的稳定性分析模型,并引入自适应遗传优化算法,实现了最危险滑动面的自动搜索.Gong等[110]基于随机马尔可夫随机场方法,研究了地层不确定性对抗滑桩加固边坡失稳概率的影响,以最小化加固边坡的失稳概率和桩的成本为双目标函数,优化设计了单排抗滑桩的设计参数,提高了加固边坡的性能.
3山区公路边坡智能监测与滑坡预测研究进展
3.1边坡智能监测
山区公路运营期间,公路边坡可能出现不同程度的变形,甚至发生滑坡、坍塌等强破坏性灾害,严重影响公路的正常使用.监测边坡的位移、土体内部应力、地下水和外部诱发因素,对边坡的稳定性评价和滑坡等灾害的预测和预警意义重大.
近年来,边坡监测技术取得了长足发展,并逐渐向高精度、自动化、智能化的方向迈进.常用的公路边坡监测技术主要有光纤光栅传感技术(FBG)、三维激光扫描技术、数字化近景摄影测量技术、合成孔径雷达干涉技术(inSAR)和全球导航卫星系统(GNSS)等[12]高新技术,它们在公路边坡监测中都有成功应用.比如,李时宜等[111]开发了分布式布里渊光纤传感技术,可以扩展光缆对局部变形的耐受度,同时提高了监测的准确度;谢谟文等[112]运用三维激光扫描技术对金坪子滑坡表面变形进行了监测研究;贾曙光等[113]基于无人机摄影测量技术,实现了高陡边坡的数字化岩体产状测量;王慧敏等[114]基于GNSS高速公路自动化监测系统,实现了地表位移和深层位移的实时管理和分析.凌建明等[12]对上述五种智能化监测技术的特点、适用性以及发展和应用现状进行了详细的回顾,并展望了该领域的发展方向.也有学者提出了一些其他的监测技术,比如:江胜华等[115]基于磁测原理,采用磁性标签制作智能石头,通过磁力梯度仪和智能石头建立边坡变形监测系统,并通过改进遗传算法,反演智能石头的运动轨迹,实现了基于磁场梯度的磁性目标定位,进而得到边坡的位移状态;梁苗等[116]基于LoRa区域无线传输技术实现区域聚集监测数据,再传输至后台处理的深部位移监测系统,实现了对西南山区某高速公路边坡变形远程自动化监测,成功解决了偏远山区网络信号差和监测数据回传难的问题.
3.2滑坡智能预测
基于已有边坡监测数据对边坡变形进行快速、合理的预测是一项关键工作,它有助于进一步快速评价边坡失稳风险和对未来滑坡灾害进行中长期预测.边坡因受到岩土体材料特性、工程水文地质条件、荷载条件、地表植被等多因素影响,其变形发展变化规律以及灾变过程难以用传统方法进行快速、准确预测.机器学习方法具有很强的处理非线性问题的能力,它在边坡智能预测中得到了广泛应用,尤其以人工神经网络(ANN)和支持向量机(SVM)模型为基础的机器学习方法在边坡预测中应用最为普遍,并发展出不同的改进方法.
在各类神经网络的应用方面,Chen等[117]基于模糊神经网络对监测数据进行位移预测,具有较高的预测精度和适用性.Cheng和Hoang[118]采用模糊k最近邻算法和萤火虫算法结合来优化模型超参数,提出了一种新型的预测边坡坍塌的模型——基于实例学习的群优化模糊(SOFIL)模型;相似地,他们还基于贝叶斯框架和k最近邻算法,提出了边坡坍塌评估的概率分析方法[119],并采用我国台湾地区高速公路的边坡样本数据验证了该方法的有效性.Wang等[120]采用基于人工鱼群算法(AFSA)的Elman神经网络模型对无人机摄影测量的位移数据进行训练并预测位移变化,与现有的Elman网络方法相比,具有更好的精度和收敛性,适用于边坡关键测点的位移预测.
在深度学习的应用方面,Yin等[121]利用卷积神经网络(CNN)处理心电图仪(ECG)输出信号的方法创建了一种空间预测模型,并选取合理的空间预测因子,在GIS的支持下对博山区公路边坡的滑坡易发性进行了预测.Das等[122]基于贝叶斯逻辑回归对印度公路沿线的滑坡敏感性进行了评估.黄武彪等[123]基于层数自适应、通道加权的CNN方法对川藏交通廊道沿线滑坡易发性进行了评价.
由于支持向量机(SVM)模型可以较好地解决监测数据量不足、维数高和非线性等一系列问题,因此,郑志成等[124]通过构造基于混合核函数改进的最小二乘支持向量机(LSSVM)模型,并引入粒子群算法(PSO),提出了邊坡位移时序预测的PSO-LSSVM算法,同时提高了预测精度和泛化能力;而Gong等[125]提出了一种结合双输出最小二乘支持向量机和粒子群优化算法的滑坡位移区间预测新方法,该方法可为滑坡位移的中长期区间预测提供准确、可靠的结果.
另外,一些其他的智能方法也应用到滑坡预测中,王志颖等[126]构造一种基于PSO-Prophet的边坡变形分析与预测模型,较好地解决了边坡变形分析与预测中周期项提取方法不确定性大和组合预测模型复杂度高的问题.仉文岗等[127]采用多元自适应回归样条曲线和集成学习LightGBM模型构建了一种基于数理-机制双驱动的滑坡变形预测方法,可在考虑岩土体参数不确定性的基础上对边坡坡脚变形进行预测.Liu等[128]先采用粗糙集理论和核主成分分析方法(RS-KPCA)提取输入数据,然后采用量子化粒子群算法和最小二乘支持向量机方法(QPSO- LSSVM)创建优化预测模型,最后采用蒙特卡洛模拟法校正预测结果,从而提出了一套边坡位移预测模型和预警方法,该模型方法具有良好的精度、收敛性和泛化能力.
地震是滑坡的主要诱因之一,常用Newmark滑块位移法来计算边坡的震后位移[129].该方法虽然原理简单、计算方便且适用性强,但若要考虑边坡土体强度参数变化、地震动强度、屈服加速度、地下水位等多因素对边坡震动位移预测的影响,机器学习方法则更为灵活.Gade等[130]基于数据驱动的人工神经网络模型,构建了一种新的Newmark滑动位移预测方程,可用于考虑地震震级、焦点机理、破裂距离、土壤顶部30 m平均横波速度和边坡屈服加速度因素下边坡位移预测.Nayek和Gade[131]采用相同的方法,针对地震动强度参数和边坡屈服加速度值的不同组合预测了边坡位移.Cho等[132]基于边坡位移有限元数据,采用ANN模型和经典回归模型对边坡地震位移进行预测,对比分析结果表明,ANN模型预测的位移随参数变化更平滑.Huang等[133]基于大规模振动台试验数据,分别采用简化的循环神经网络(Simple-RNN)模型、长短期记忆(LSTM)神经网络模型和循环门单元(GRU)神经网络模型对地震荷载动态响应的时序位移进行预测,结果表明,Simple- RNN模型在分析边坡的地震动力响应方面表现较好.Wang等[134]提出了一个利用极端梯度提升模型(XGBoost)和子集仿真(SS)的机器学习框架(SS- XGBoost)来预测边坡滑动位移.Macedo等[135]提出了多種机器学习模型来估计地震引起的边坡位移量,其中,Logistic回归和Bray-Macedo模型(即BM2019模型)出错率较低.
3.3滑坡智能识别
在大面积滑坡灾害发生时快速获取滑坡区域分布、数量、规模等灾情信息对救援决策和防灾减灾都有着重要意义[136]随着航空航天技术和光学遥感技术的发展,高分辨率、多/高光谱、多平台、多时相遥感成像为滑坡的检测识别和灾情快速提取提供了新的技术手段.滑坡的识别结果可以反映滑坡分布情况,是滑坡易发性等风险评价研究的基础[137].巨袁臻等[138]利用掩膜区域卷积神经网络(Mask R- CNN)目标检测模块对中国典型黄土滑坡进行了自动识别.陈善静等[136]提出了一种基于多源遥感时空谱特征融合的滑坡灾害检测方法,其中基于SVM实现了对滑坡目标地物的精确识别.余加勇等[139]基于无人机倾斜摄影测量数据,重构了公路边坡三维实景模型和三维点云模型,引入多尺度模型与模型点云比较(M3C2)算法对三维点云数据进行分析,实现了滑坡、坍塌、落石等灾害场景的自动识别.
3.4岩质边坡结构面智能识别
岩体中结构面调查和产状分析是开展岩体稳定性分析研究的基础.随着监测和测量技术的不断发展,新型的非接触式测量技术被广泛用于规模较大、地质环境复杂的边坡工程,具有便捷、可靠、安全的特点.比如,三维激光扫描技术可以短时间内获得岩体结构面的高精度点云数据[140];无人机摄影测量技术随着运动恢复结构(SfM)和多视图立体匹配(MVS)算法的成熟,可以轻松地对拍摄照片进行三维模型重建,更加适应复杂地形的监测[141].而后,基于生成的点云数据或三维岩体结构模型智能识别结构面参数的研究也快速发展起来.Chen等[142]基于k均值聚类算法,提出了一种从三维点云中自动提取不连续性方向的新方法.葛云峰等[143]利用改进的区域生长法与解析几何理论对点云数据处理,实现了岩体结构面智能识别与信息提取.宁浩等[144]通过基于霍夫空间变换算法和深度学习计算了点云的法向量,并对点云进行赋色,提出了一种自动识别结构面及产状信息的方法.王培涛等[145]基于敏感性参数近邻点数、夹角阈值和过滤因子的结构面识别算法,实现了对三维复杂点云的优势结构面倾向、倾角产状信息快速识别.陈昌富等[146]基于k最近邻(KNN)聚类算法及主成分分析法(PCA)确定了边坡三维模型中结构面的位置和产状参数.
在充足的数据样本下,深度学习方法的识别效果更有优势,王鹏宇和王述红[147]基于Tensorflow建立了岩质边坡图像分析的CNN模型,并对模型进行了训练和测试,实现了岩质边坡岩石的自动识别与分类,该模型具有良好的鲁棒性.张紫杉等[148]采用空洞卷积算法与高斯混合模型-最大期望算法(GMM-EM)结合,对岩体坡面裂隙网络进行快速智能识别与参数化表征,达到了较高的准确率.
3.5岩土体力学参数智能反演
岩土体参数的分析与确定是边坡稳定性评价和设计的基础.反演分析方法可为准确估计岩土体参数提供有效的手段.近年来,随着计算技术和人工智能技术的发展,ANN、GA、SA、SVM等人工智能方法被广泛引入反分析领域,岩土工程反分析正朝着多维化、智能化和高效化方向发展.
边坡位移反分析法是确定边坡岩土体参数值的一种有效方法.漆祖芳等[149]基于粒子迁徙和变异的粒子群优化算法(MVPSO)搜索最佳的支持向量机(v-SVR)模型参数,提出了一种位移反分析方法,该法与基于遗传算法BP神经网络模型(BP-GA)和v-SVR-GA相比,反演精度和效率更高.Liu等[150]基于梯度提升决策树算法构建元模型,分别构建了以频率推理的确定性反分析和以贝叶斯推理的概率反分析两种位移反分析方法.由于两种方法对参数空间具有不同的敏感度,可以互补分析边坡的参数与位移关系.
概率反分析方法可以更好地考虑地质力学参数的不确定性.Zhang等[151]在贝叶斯框架下评估了边坡土体中水力参数、黏聚力和内摩擦角的不确定性及其对边坡稳定性预测的影响.Wang等[152]基于最大似然估计和马尔可夫链蒙特卡罗模拟(MCMC)反算了台北3号高速公路滑坡中岩土体的内摩擦角和锚固力参数.Li等[153]集成贝叶斯方法和多输出支持矢量机模型提出了一种概率反分析方法,并合理地应用于龙潭水电站岩质边坡的杨氏模量和侧压系数分析.Jiang等[154]提出基于结构可靠度进行贝叶斯更新(BUS)的方法,对空间变异的土体不排水抗剪强度参数进行概率反分析和边坡可靠性更新,有效地避免了“维数灾难”和似然乘数评估,显著提高了计算精度.江巍等[155]提出了利用BP神经网络实现岩土体抗剪强度参数的逆向迭代修正反演的方法.Liu等[156]使用基于子集模拟的贝叶斯更新的方法和边坡监测数据,反演出土体的水力参数.仇文岗等[127]基于有限的孔压实测数据,运用DREAM_zs算法,对降雨入渗非饱和土坡的岩土体变形、水力和强度参数进行了概率反演和有效更新,该方法计算效率高且收敛速度快.
4展望
1)在边坡的确定性分析方法中,基于中值安全系数的极限平衡法或极限分析法仍然是最重要的两种分析手段,但由于其在建模时假定条件较多,无法较全面地考虑山区复杂的地质条件和环境因素对公路边坡稳定性的影响,导致其对山区公路边坡稳定性的评价往往与工程实际不符.虽然基于智能算法和机器学习的分析方法,可以考虑多种因素对边坡稳定性的影响,但由于其理论尚不完善、计算相对繁琐、实用性不强,目前尚未被业界广泛接受.因此,对于复杂环境和工况下的山区公路边坡,亟须发展方法可靠、计算高效、适用性强的稳定性分析智能计算方法.
2)虽然业界已普遍认识到山区公路边坡稳定性分析中存在大量的随机性和不确定性因素,并逐渐接受了采用可靠度方法来评价边坡的稳定性,而且大量智能算法和机器学习方法也在边坡可靠度计算中得到成功应用,但由于对山区岩土体物理力学参数的统计分析严重缺乏,导致可靠度分析结果往往与实际差异较大.因此,应引入现代试验技术与方法、数据挖掘技术和人工智能方法,大力开展公路边坡岩土体参数的数理统计分析,并加强对边坡可靠度计算模型和可靠性评价标准的研究.
3)在山区公路边坡处治智能设计方面,人工智能技术的应用还不够成熟,相关的研究還较少.今后应加强引入人工智能方法和智能试验技术,开展边坡加固结构工作机理和实用的智能优化设计计算方法研究.
4)在山区公路边坡智能监测和预测方面,尝试采用基于人工智能的“天-空-地”一体化联合监测方法对公路沿线边坡开展多层次、多角度、系统性的监测,实时监控并分析边坡的变形发育特征,及时识别滑坡灾害并做出预测预警.
参考文献
[1]SENGUPTA A,UPADHYAY A. Locating the critical failure surface in a slope stability analysis by genetic algorithm [J]. Applied Soft Computing,2009,9(1):387-392.
[2]CHENG Y M. Global optimization analysis of slope stability by simulated annealing with dynamic bounds and Dirac function[J]. Engineering Optimization,2007,39(1):17-32.
[3]陈昌富,杨宇.边坡稳定性分析水平条分法及其进化计算[J].湖南大学学报(自然科学版),2004,31(3):72-75.
CHEN C F,YANG Y. Horizontal slice method of slope stability analysis based on evolutionary algorithm [J]. Journal of Hunan University (Natural Sciences),2004,31(3):72-75. (In Chinese)
[4]金亮星,冯琦璇,潘卓夫.基于Morgenstern-Price法和改进径向移动算法的边坡稳定性分析[J].中国公路学报,2018,31 (2):39-47.
JIN L X,FENG Q X,FAN Z F. Slope stability analysis based on Morgenstern-Price method and improved radial movement optimization algorithm [J]. China Journal of Highway and Transport,2018,31(2):39-47. (In Chinese)
[5]SAMUI P. Slope stability analysis:a support vector machine ap- proach[J]. Environmental Geology,2008,56(2):255-267.
[6]SINGH J,BANKA H,VERMA A K. A BBO-based algorithm for slope stability analysis by locating critical failure surface[J]. Neural Computing and Applications,2018,31(10):6401-6418.
[7]PONTEROSSO P,FOX D S. Optimization of reinforced soil embankments by genetic algorithm [J]. International Journal for Numerical and Analytical Methods inGeomechanics,2000,24(4):425-433.
[8]唐晓松,郑颖人,段永胜,等.人工智能在埋入式抗滑桩设计中的应用[J].地下空间与工程学报,2010,6(2):375-381.
TANG X S,ZHENG YR,DUAN YS,et al. Application of artifi- cal intelligence in the design of embedded anti-slide piles[J]. Chinese Journal of Underground Space and Engineering,2010,6 (2):375-381.(In Chinese)
[9]周苏华,邢静康,张运强,等.基于模糊层次分析法的预应力锚索加固顺层边坡稳定性评价[J].安全与环境学报,2020,20 (5):1695-1704.
ZHOU S H,XING J K,ZHANG Y Q,et al. An assessment model based on the hierarchical fuzzy analysis process for the bedding slope with the prestressed anchor cable frame reinforcement[J]. Journal of Safety and Environment,2020,20(5):1695-1704. (In Chinese)
[10]SARI P A,SUHATRIL M,OSMAN N,et al. Developing a hybrid adoptive neuro-fuzzy inference system in predicting safety of factors of slopes subjected to surface eco-protection techniques [J]. Engineering with Computers,2019,36(4):1347-1354.
[11]何滿潮,任树林,陶志刚.滑坡地质灾害牛顿力远程监测预警系统及工程应用[J].岩石力学与工程学报,2021,40(11):2161-2172.
HE M C,REN S L,TAO Z G. Remote monitoring and forecasting system of Newton force for landslide geological hazards and its engineering application[J]. Chinese Journal of Rock Mechanics and Engineering,2021,40(11):2161-2172.(In Chinese)
[12]凌建明,张玉,满立,等.公路边坡智能化监测体系研究进展[J].中南大学学报(自然科学版),2021,52(7):2118-2136.
LING J M,ZHANG Y,MAN L,et al. Research progress of intelligent monitoring system for highway slope[J]. Journal of Central South University (Scienceand Technology),2021,52(7):2118-2136.(In Chinese)
[13]KENNEDY J,EBERHART R. Particle swarm optimization [C]//Proceedings of ICNN,95. New York:IEEE,1995:1942-1948.
[14]DORIGO M,GAMBARDELLA L M. Ant colony system:a cooperative learning approach to the travelling salesman problem[J]. IEEE Transactions on Evolutionary Computation,1997,1(1):53-66.
[15]KHAJEHZADEH M,TAHA M R,EL-SHAFIE A,et al. A modified gravitational search algorithm for slope stability analysis[J]. Engineering Applications of Artificial Intelligence,2012,25(8):1589-1597.
[16]KANG F,LI J,MA Z. An artificial bee colony algorithm for locating the critical slip surface in slope stability analysis[J]. Engineering Optimization,2013,45(2):207-223.
[17]LISH,WULZ,LUO X H. A novel method for locating the critical slip surface of a soil slope[J]. Engineering Applications of Artificial Intelligence,2020,94(1):103733.
[18]HIMANSHU N,KUMAR V,BURMAN A,et al. Grey wolf optimization approach for searching critical failure surface in soil sloped[J]. Engineering with Computers,2020,37(3):2059-2072.
[19]NI S H,LU P C,JUANG C H. A fuzzy neural network approach to evaluation of slope failure potential[J]. Computer-Aided Civil and Infrastructure Engineering,1996,11(1):59-66.
[20]LIN S,ZHENG H,HAN B,et al. Comparative performance of eight ensemble learning approaches for the development of models of slope stability prediction[J]. Acta Geotechnica,2022,17(4):1477-1502.
[21]GOH A T. Genetic algorithm search for critical slip surface in multiple-wedge stability analysis[J]. Canadian Geotechnical Jour- nal,1999,36(2):382-391.
[22]ZHU J F,CHEN C F. Search for circular and noncircular critical slip surfaces in slope stability analysis by hybrid genetic algorithm [J]. Journal of Central South University,2014,21(1):387-397.
[23]CEN W,LUO J,YU J,et al. Slope stability analysis using genetic simulated annealing algorithm in conjunction with finite element method[J]. KSCE Journal of Civil Engineering,2019,24 (1):30-37.
[24]ZHOU X P,HUANG X C,ZHAO X F. Optimization of the critical slip surface of three-dimensional slope by using an improved genetic algorithm [J]. International Journal of Geomechanics,2020,20(8):04020120.
[25]XU Z,ZHOU X. Determination of the critical slip surface of slope based on the improved quantum genetic algorithm and random forest [J]. KSCE Journal of Civil Engineering,2022,26(5):2126- 2138.
[26]KIRKPATRICK S,GELATT C D J,VECCHI M P. Optimization by simulated annealing[J].Science,1983,220(4598):671-680.
[27]刘华强,陆明志,殷宗泽.基于模拟退火算法的边坡临界滑面搜索方法[J].岩石力学与工程学报,2008,27(S2):3686-3691.
LIUHQ,LUMZ,YINZ Z. Analytical method of searching noncircular slip surface based on simulated annealing optimization algorithm [J]. Chinese Journal of Rock Mechanics and Engineering,2008,27(S2):3686-3691. (InChinese)
[28]李亮,迟世春,林皋.禁忌模拟退火复合形法及其在边坡稳定性分析中的应用[J].岩石力學与工程学报,2006,24(18):3342-3349.
LI L,CHI S C,LIN G. Tabu simulated annealing complex method and its application to slope stability analysis[J]. Chinese Journal of Rock Mechanics and Engineering,2006,24(18):3342-3349. (In Chinese)
[29]李亮,陈祖煜,迟世春,等.基于NURBS表示的三维土坡稳定分析[J].岩土工程学报,2008,30(2):212-218.
LI L,CHEN Z Y,CHI S C,et al. Three-dimensional slope stability analysis based on NURBS simulation[J]. Chinese Journal of Geotechnical Engineering,2008,30(2):212-218.(In Chinese)[30]徐飞,徐卫亚,刘造保,等.基于PSO-PP的边坡稳定性评价[J].岩土工程学报,2011,33(11):1708-1713.
XU F,XU W Y,LIU Z B,et al. Slope stability evaluation based on PSO-PP [J]. Chinese Journal of Geotechnical Engineering,2011,33(11):1708-1713.(In Chinese)
[31]杨善统,姜清辉,尹涛,等.边坡临界滑面搜索的改进粒子群优化算法[J].岩土工程学报,2015,37(8):1411-1417.
YANG S T,JIANG Q H,YIN T,et al. Search of critical slip surface of slopes using improved particle swarm optimization method [J]. Chinese Journal of Geotechnical Engineering,2015,37(8):1411-1417.(In Chinese)
[32]陈昌富,龚晓南.混沌扰动启发式蚁群算法及其圆弧临界滑动面搜索中的应用[J].岩石力学与工程学报,2003,23(20):3450-3453.
CHEN C F,GONG X N. Heuristic ant colony algorithm involving chaos operator and its application to search for critical slip surface of slope[J]. Chinese Journal of Rock Mechanics and Engineering,2003,23(20):3450-3453.(In Chinese)
[33]石露,李小春,任偉,等.蚁群算法与遗传算法融合及其在边坡临界滑动面搜索中的应用[J].岩土力学,2009,30(11):3486-3492.
SHI L,LI X C,REN W,et al. Hybrid of ant colony algorithm and genetic algorithm and its application to searching critical slope slip surface[J]. Rock and Soil Mechanics,2009,30(11):3486- 3492.(In Chinese)
[34]GAO W. Premium-penalty ant colony optimization and its application in slope stability analysis[J]. Applied Soft Computing,2016:480-488.
[35]GAO W. Determination of the noncircular critical slip surface in slope stability analysis by meeting ant colony optimization[J]. Journal of Computing in Civil Engineering,2016,30(2):1-10.
[36]YANG Y,WU W,ZHANG J,et al. Determination of critical slip surface and safety factor of slope using the vector sum numerical manifold method and MAX-MIN ant colony optimization algorithm [J]. Engineering Analysis with Boundary Elements,2021,127:64-74.
[37]RAIHAN T M,MOHAMMAD K,MAHDIYEH E. A new hybrid algorithm for global optimization and slope stability evaluation[J]. Journal of Central South University,2013,20(11):3265-3273.
[38]蒋建国,谭雅,董立明,等.改进的万有引力搜索算法在边坡稳定分析中的应用[J].岩土工程学报,2016,38(3):419-425. JIANG J G,TAN Y,DONG L M,WANG C,et al. Application of modified gravitational search algorithm in slope stability analysis [J]. Chinese Journal of Geotechnical Engineering,2016,38(3):419-425.(In Chinese)
[39]MA L,ZHAO J,ZHANG J,et al. Slope stability analysis based on leader dolphins herd algorithm and simplified bishop method [J]. IEEE Access,2021,9:28251-28259.
[40]LI S,ZHONG C,LUO X. Locating critical slip surfaces of soil slopes with heuristic algorithms:a comparative study[J]. Expert Systems with Applications,2022,191:116214.
[41]陈光耀,汪明武,金菊良.基于CMFOA-SVM的边坡稳定性评价模型[J/OL].长江科学院院报:1-9(2021-09-02)[2022-07- 01].http://kns.cnki.net/kcms/detail/42.1171.TV.20210902.1602.008.html.
CHEN G Y,WANG M W,JIN J L. CMFOA-SVM model for the evaluation of slope stability[J/OL]. Journal of Yangtze River Scientific Research Institute:1-9(2021-09-02)[2022-07-01]. http://kns.cnki.net/kcms/detail/42.1171.TV.20210902.1602.008.htm.(In Chinese)
[42]SUYKENS JAK,VANDEW ALLE J. Least squares support vector machine classifiers[J]. Neural Processing Letters,1999,9(3):293-300.
[43]XUE X. Prediction of slope stability based on hybrid PSO and LSSVM[J]. Journal of Computing in Civil Engineering,2017,31 (1):1-10.
[44]ZENG F,NAIT A M,MOHAMMED A S,et al. Improving the performance of LSSVM model in predicting the safety factor for circular failure slope through optimization algorithms[J]. Engineering with Computers,2021:1-12.
[45]CAI Z L,MENG Y D,WANG R Y,et al. Slope stability forecast of LS-SVM based on chaos genetic algorithm optimization[J]. Applied Mechanics and Materials,2013,405/406/407/408:2384- 2390.
[46]LI B,LI D,ZHANG Z,et al. Slope stability analysis based on quantum-behaved particle swarm optimization and least squares support vector machine[J]. Applied Mathematical Modelling,2015,39(17):5253-5264.
[47]陈昌富,杨宇.基于HGA-ANN驱动边坡稳定评价T-S型模糊推理系统[J].岩石力学与工程学报,2005,24(19):61-66. CHEN C F,YANG Y. Fuzzy reasoning system driven by HGA- ANN for estimation of slope stability[J]. Chinese Journal of Rock Mechanics and Engineering,2005,24(19):61-66.(In Chinese)
[48]GORDAN B,JAHED ARMAGHANI D,HAJIHASSANI M,et al. Prediction of seismic slope stability through combination of particle swarm optimization and neural network[J]. Engineering with Computers,2015,32(1):85-97.
[49]DAS S K,BISWAL R K,SIVAKUGAN N,et al. Classification ofslopes and prediction of factor of safety using differential evolution neural networks [J]. Environmental Earth Sciences,2011,64 (1):201-210.
[50]KHAJEHZADEH M,TAHA M R,KEAWSAWASVONG S,et al. An effective artificial intelligence approach for slope stability evaluation[J]. IEEE Access,2022,10:5660-5671.
[51]FOONG L K,MOAYEDI H. Slope stability evaluation using neural network optimized by equilibrium optimization and vortex search algorithm [J]. Engineering with Computers,2021,38 (S2):1269-1283.
[52]LIAO Z,LIAO Z. Slope stability evaluation using backpropagation neural networks and multivariate adaptive regression splines [J]. Open Geosciences,2020,12(1):1263-1273.
[53]胡軍,董建华,王凯凯,等.边坡稳定性的CPSO-BP模型研究[J].岩土力学,2016,37(S1):577-582.
HU J,DONG J H,WANG K K,et al. Research on CPSO-BP model of slope stability [J]. Rock and Soil Mechanics,2016,37 (S1):577-582.(In Chinese)
[54]HSIAO C H,CHEN A Y,GE L,et al. Performance of artificial neural network and convolutional neural network on slope failure prediction using data from the random finite element method[J]. Acta Geotechnica,2022:1-11.
[55]QI C,TANG X. A hybrid ensemble method for improved prediction of slope stability[J]. International Journal for Numerical and Analytical Methods in Geomechanics,2018,42(15):1823-1839.
[56]QI C,TANG X. Slope stability prediction using integrated metaheuristic and machine learning approaches:a comparative study [J]. Computers and Industrial Engineering,2018,118:112-122.
[57]SUN J,WU S,ZHANG H,et al. Based on multi-algorithm hybrid method to predict the slope safety factor-stacking ensemble learning with bayesian optimization[J]. Journal of Computational Science,2022,59:101587.
[58]LIN S,ZHENG H,HAN C,et al. Evaluation and prediction of slope stability using machine learning approaches[J]. Frontiers of Structural and Civil Engineering,2021,15(4):821-833.
[59]MAHMOODZADEH A,MOHAMMADI M,FARID H A H,et al. Prediction of safety factors for slope stability:comparison of machine learning techniques[J]. Natural Hazards,2021,111(2):1771-1799.
[60]KARIR D,RAY A,KUMAR B A,et al. Stability prediction ofa natural and man-made slope using various machine learning algo- rithms[J]. Transportation Geotechnics,2022,34:1-13.
[61]LIN Y,ZHOU K,LI J. Prediction of Slope Stability Using Four Supervised Learning Methods [J]. IEEE Access,2018,6:31169-31179.
[62]李典慶,唐小松,周创兵.含相关非正态变量边坡可靠度分析的认知聚类分区方法[J].岩土工程学报,2011,33 (6):875-882.
LI D Q,TANG X S,ZHOU C B,Reliability analysis of slope stability involving correlated non-normal variables using knowledgebased clustered partitioning method[J]. Chinese Journal of Geotechnical Engineering,2011,33(6):875-882.(In Chinese)
[63]苏永华,赵明华,蒋德松,等.响应面方法在边坡稳定可靠度分析中的应用[J].岩石力学与工程学报,2006,25(7):14171424.
SU Y H,ZHAO M H,JIANG D S,et al. Application of response surface method to reliability analysis of slope stability[J]. Chinese Journal of Rock Mechanics and Engineering,2006,25(7):1417-1424.(In Chinese)
[64]LI S,ZHAO H B,RU Z. Slope reliability analysis by updated support vector machine and Monte Carlo simulation[J]. Natural Hazards,2013,65(1):707-722.
[65]毛凤山,陈昌富,朱世民.代理模型方法及其在岩土工程中的应用综述[J].地基处理,2020,2(4):295-306.
MAO F S,CHEN C F,ZHU S M. Surrogate model method and its application in geotechnical engineering[J]. Journal of Ground Improvement,2020,2(4):295-306.(In Chinese)
[66]SAMUI P,LANSIVAARA T,KIM D. Utilization relevance vector machine for slope reliability analysis[J]. Applied Soft Computing,2011,11(5):4036-4040.
[67]苏永华,罗正东,张盼凤,等.基于Kriging的边坡稳定可靠度主动搜索法[J].岩土工程学报,2013,35(10):1863-1869.
SU Y H,LUO Z D,ZHANG P F,et al. Active searching algorithm for slope stability reliability based on Kriging model[J]. Chinese Journal of Geotechnical Engineering,2013,35(10):1863- 1869.(In Chinese)
[68]KANG F,LI J S,LI J J. System reliability analysis of slopes using least squares support vector machines with particle swarm optimization[J]. Neurocomputing,2016,209:46-56.
[69]朱彬,裴华富,杨庆.基于高斯过程回归的响应面法及边坡可靠度分析[J].岩土工程学报,2019,41(S1):209-212.
ZHU B,PEI H F,YANG Q. Gaussian process regression-based response surface method and reliability analysis of slopes[J]. Chinese Journal of Geotechnical Engineering,2019,41(S1):209- 212.(In Chinese)
[70]張天龙,曾鹏,李天斌,等.基于主动学习径向基函数的边坡系统可靠度分析[J].岩土力学,2020,41(9):3098-3108.
ZHANG T L,ZENG P,LI T B,et al. System reliability analyses of slopes based on active-learning radial basis function[J]. Rock and Soil Mechanics,2020,41(9):3098-3108.(In Chinese)
[71]谢梦龙,叶新宇,张升,等.LASSO算法及其在边坡稳定性分析中的应用[J].岩土工程学报,2021,43(9):1724-1729.
XIE M L,YE X Y,ZHANG S,et al. LASSO algorithm and its application in slope stability analysis[J]. Chinese Journal of Geotechnical Engineering,2021,43(9):1724-1729.(In Chinese)[72]邓志平,李典庆,曹子君,等.考虑地层变异性和土体参数变异性的边坡可靠度分析[J].岩土工程学报,2017,39(6):986-995.
DENG Z P,LI D Q,CAO Z J,et al. Slope reliability analysis considering geological uncertainty and spatial variability of soil parameters[J]. Chinese Journal of Geotechnical Engineering,2017,39 (6):986-995.(In Chinese)
[73]GRIFFITHS D V,HUANG J,FENTON G A. Probabilistic infinite slope analysis[J]. Computers and Geotechnics,2011,38(4):577-584.
[74]LI D Q,JIANG S H,CAO Z J,et al. A multiple response-surface method for slope reliability analysis considering spatial variability of soil properties [J]. Engineering Geology,2015,187:60-72.
[75]QIN Y,ZHU F,XU D. Effect of the spatial variability of soil parameters on the deformation behavior of excavated slopes [J]. (Computers and Geotechnics,2021,136:1-15.
[76]杨智勇,李典庆,曹子君,等.基于广义子集模拟样本加权法的边坡多失效模式可靠度分析[J].岩石力学与工程学报,2018,37(3):630-641.
YANG Z Y,LI D Q,CAO Z J,et al. Efficient analysis of slope reliability with multiple failure modes using sample weighting method in generalized subset simulation [J]. Chinese Journal of Rock Mechanics and Engineering,2018,37(3):630-641. (In Chinese )
[77]姬建,姜振,殷鑫,等.边坡随机场数字图像特征CNN深度学习及可靠度分析[J/OL].岩土工程学报:1-11(2022-02-16)http://kns.cnki.net/kcms/detail/32.1124.TU.20220216.1457.002.html.
JI J,JIANG Z,YIN X,et al. Slope reliability analysis based on deep learning of digital images of random fields using CNN[J/OL]. Chinese Journal of Geotechnical Engineering:1-11(2022-02-16)http://kns.cnki.net/kcms/detail/32.1124.TU.20220216.1457.002.html.(In Chinese)
[78]ZAI D,PANG R,XU B,et al. Slope system stability reliability analysis with multi-parameters using generalized probability density evolution method[J]. Bulletin of Engineering Geology and the Environment,2021,80(11):8419-8431.
[79]LI D Q,QI X H,CAO Z J,et al. Evaluating slope stability uncertainty using coupled Markov chain[J]. Computers and Geotech- nics,2016,73:72-82.
[80]LIU L L,CHENG Y M,PAN Q J,et al. Incorporating stratigraphic boundary uncertainty into reliability analysis of slopes in spatially variable soils using one-dimensional conditional Markov chain model[J]. Computers and Geotechnics,2020,118:1-13.
[81]YI P,WEI K,KONG X,et al. Cumulative PSO-Kriging model for slope reliability analysis[J]. Probabilistic Engineering Mechan- ics,2015,39:39-45.
[82]XIAO H,ZHANG Z,CHEN L,et al. An improved spatio-temporal kriging interpolation algorithm and its application in slope[J]. IEEE Access,2020,8:90718-90729.
[83]姬建,王樂沛,廖文旺,等.基于WUS概率密度权重法的边坡稳定系统可靠度分析[J].岩土工程学报,2021,43(8):1492-1501.
JI J,WANG L P,LIAO W W,et al. System reliability analysis of slopes based on weighted uniform simulation method[J]. Chinese Journal of Geotechnical Engineering,2021,43(8):1492-1501. (In Chinese)
[84]YAO W,LI C,YAN C,et al. Slope reliability analysis through Bayesian sequential updating integrating limited data from multiple estimation methods[J]. Landslides,2022,19(5):1101-1117.
[85]CONTRERAS L F,BROWN E T. Slope reliability and back analysis of failure with geotechnical parameters estimated using Bayesian inference[J]. Journal of Rock Mechanics and Geotechnical Engineering,2019,11(3):628-643.
[86]刘阳,张建经,李孟芳,等.基于模糊理论与SVM的边坡地震失稳规模贝叶斯网络评估方法[J].岩石力学与工程学报,2019,38(S1):2807-2815.
LIU Y,ZHANG J J,LI M F,et al. Fuzzy theory- and SVM- based Bayesian network assessment method for slope seismic instability scale[J]. Chinese Journal of Rock Mechanics and Engineering,2019,38(S1):2807-2815.(In Chinese)
[87]徐冲,刘保国,刘开云,等.基于组合核函数的高斯过程边坡角智能设计[J].岩土力学,2010,31(3):821-826.
XU C,LIU B G,LIU K Y,et al. Slope angle intelligent design based on Gaussian process with combinatorial kernel function[J]. Rock and Soil Mechanics,2010,31(3):821-826.(In Chinese)[88]张志军,熊正为,丁德馨,等.圆弧破坏边坡反演设计的ANN方法与ANFIS方法的比较研究J].岩土力学,2006,27(1):159-162.
ZHANG Z J,XIONG Z W,DING D X,et al. A comparative study of ANN-based and ANFIS-based approaches for inverse design of circular failure slopes[J]. Rock and Soil Mechanics,2006,27 (1):159-162.(In Chinese)
[89]ZHOU X,CHEN J,CHEN Y,et al. Bayesian-based probabilistic kinematic analysis of discontinuity-controlled rock slope instabilities[J]. Bulletin of Engineering Geology and the Environment,2016,76(4):1249-1262.
[90]YAN J,CHEN J,LI Y,et al. Kinematic-based failure angle analysis for discontinuity-controlled rock slope instabilities:a case study of Ren Yi Peak Cluster in Fusong County,China[J]. Natural Hazards,2021,111(3):2281-2296.
[91]XIE H,DONG J,DENG Y,et al. Prediction model of the slope angle of rocky slope stability based on random forest algorithm [J]. Mathematical Problems in Engineering,2022,2022:9441411.
[92]《中國公路学报》编辑部.中国路基工程学术研究综述·2021 [J].中国公路学报,2021,34(3):1-49.
Editorial Department of China Journal of Highway and Transport. Review on China's subgrade engineering research·2021 [J]. China Journal of Highway and Transport,2021,34(3):1-49.(In Chinese)
[93]SAFA M,SARI P A,SHARIATI M,et al. Development of neuro- fuzzy and neuro-bee predictive models for prediction of the safety factor of eco-protection slopes[J]. Physica A:Statistical Mechanics and its Applications,2020,550:1-18.
[94]LIU L,DOU Y,QIAO J. Evaluation method of highway plant slope based on rough set theory and analytic hierarchy process:a case study in Taihang Mountain,Hebei,China[J]. Mathematics,2022,10(8):1-17.
[95]LIU D,LIU C,TANG Y,et al. A GA-BP neural network regression model for predicting soil moisture in slope ecological protection[J]. Sustainability,2022,14(3):1386-1399.
[96]FARSHIDFAR N,KESHAVARZ A,MIRHOSSEINI S M. Pseudo-static seismic analysis of reinforced soil slopes using the horizontal slice method [J]. Arabian Journal of Geosciences,2020,13(7):283-296.
[97]SHINODA M,MIYATA Y. PSO-based stability analysis of unreinforced and reinforced soil slopes using non-circular slip surface [J].Acta Geotechnica,2018,14(3):907-919.
[98]BAHOOTOROODY F,KHALAJ S,LEONI L,et al. Reliability estimation of reinforced slopes to prioritize maintenance actions [J]. International Journal of Environmental Research and Public Health,2021,18(2):373-384.
[99]GANDOMI A H,KASHANI A R,ROKE D A,et al. Optimization of retaining wall design using recent swarm intelligence techniques [J]. EngineeringStructures,2015,103:72-84.
[100]侯超群,檀奕,阮晓波,等.基于遗传算法的临水加筋土挡墙拟静力内部稳定分析[J].公路交通科技,2022,39(1):65-71.
HOU C Q,TAN Y,RUAN X B,et al. Analysis on seismic internal stability of waterfront reinforced retaining wall using pseudostatic approach based on genetic algorithm[J]. Journal of Highway and Transportation Research and Development,2022,39(1):65-71.(In Chinese)
[101]朱剑锋,陈昌富,徐日庆.土钉墙内部稳定性分析自适应禁忌变异遗传算法[J].岩土力学,2010,31(5):1663-1669.
ZHU JF,CHEN C F,XU R Q. Application of ATMGA to interior stability analysis of soil-nailing wall [J]. Rock and Soil Mechanics,2010,31(5):1663-1669.(In Chinese).
[102]董建华,朱彦鹏.地震作用下土钉支护边坡永久位移计算方法研究[J].工程力学,2011,28(10):101-110.
DONG J H,ZHU Y P. Permanent displacement assessment of slope protected by soil nailing retaining wall under earthquake[J]. Engineering Mechanics,2011,28(10):101-110.(In Chinese)
[103]惠趁意,朱彦鹏,叶帅华.预应力锚杆复合土钉支护边坡稳定性分析[J].岩土工程学报,2013,35(S2):325-329.
HUI C Y,ZHU Y P,YE S H. Stability analysis of composite soilnailing wall with prestressed anchors[J]. Chinese Journal of Geotechnical Engineering,2013,35(S2):325-329.(In Chinese)
[104]房光文,朱彦鹏,叶帅华,等.考虑模糊随机性的土钉加固边坡可靠度分析[J].岩土工程学报,2021,43(S1):122-126.
FANG G W,ZHU Y P,YE S H,et al. Reliability analysis of soil nailing-reinforced slopes considering fuzzy randomness[J]. Chinese Journal of Geotechnical Engineering,2021,43(S1):122- 126.(In Chinese)
[105]罗辉,杨仕教,喻清,等.基于FEM-RSM-GA的边坡锚杆设计可靠性反问题研究[J].武汉理工大学学报,2010,32(9):93-96.
LUO H,YANG S J,YU Q,et al. Research on inverse problem of slope anchor parameters design based on FEM-RSM-GA method [J]. Journal of Wuhan University of Technology,2010,32(9):93-96.(In Chinese)
[106]尹志凯,卢坤林,石峰,等.基于改进差分进化算法的三维边坡锚固位置优化[J].岩土工程学报,2020,42(7):1322-1330.
YIN Z K,LU K L,SHI F,et al. Optimization of anchorage location of three dimensional slopes based on improved differential evolution algorithm[J]. Chinese Journal of Geotechnical Engineering,2020,42(7):1322-1330.(In Chinese)
[107]谢全敏,徐善柱,但山林,等.既有加固边坡锚杆结构健康状态诊断方法及其应用研究[J].湖南大学学报(自然科学版),2018,45(S0):69-73.
XIE Q M,XU S Z,DAN S L,et al. Study on diagnosing methods and applications of health status for anchor structure in an existing reinforced slope[J]. Journal of Hunan University(Natural Sciences),2018,45(S0):69-73.(In Chinese)
[108]杨波,郑颖人,唐晓松,等.人工智能在双排全长式抗滑桩设计中的应用[J].地下空间与工程学报,2010,6(2):358-363.
YANG B,ZHENG Y R,TANG X S,et al. Application of artifical intelligence in the design of full-length anti-slide pile[J]. Chinese Journal of Underground Space and Engineering,2010,6 (2):358-363.(In Chinese)
[109]梁冠亭,陈昌富,朱剑锋,等.基于M-P法的抗滑樁支护边坡稳定性分析[J].岩土力学,2015,36(2):451-469.
LIANG G T,CHEN C F,ZHU J F,et al. Stability analysis of pile stabilized slope based on Morgenstern-Price method[J]. Rock and Soil Mechanics,2015,36(2):451-469.(In Chinese)
[110]GONG W,TANG H,WANG H,et al. Probabilistic analysis and design of stabilizing piles in slope considering stratigraphic uncertainty[J]. Engineering Geology,2019,259:1-14.
[111]李時宜,李浩,季文斌.基于布里渊光时域反射仪的边坡监测光纤传感器结构[J].光子学报,2021,50(9):0906005.
LI S Y,LI H,JI W B,et al. Optical fiber sensing structure for slope monitoring based on brillouin optical time domain reflectometer [J]. Acta PhotonicaSinica,2021,50(9):0906005.(In Chinese)
[112]谢谟文,胡嫚,王立伟.基于三维激光扫描仪的滑坡表面变形监测方法:以金坪子滑坡为例[J].中国地质灾害与防治学报,2013,24(4):85-92.
XIE M W,HU M,WANG L W. Landslide monitoring by threedimensional laser scanner-case study of the displacement detection of the Jinpingzi landslide(Southwest,China)[J]. ZhongguoDizhizaihai Yu FangzhiXuebao,2013,24(4):85-92.(In Chinese)
[113]贾曙光,金爱兵,赵怡晴.无人机摄影测量在高陡边坡地质调查中的应用[J].岩土力学,2018,39(3):1130-1136.
JIA S G,JIN A B,ZHAO Y Q. Application of UAV oblique photogrammetry in the field of geology survey at the high and steep slope [J]. Rock and Soil Mechanics,2018,39(3):1130-1136.(In Chinese)
[114]王慧敏,罗忠行,肖映城,等.基于GNSS技术的高速公路边坡自动化监测系统[J].中国地质灾害与防治学报,2020,31(6):60-68.
WANG H M,LUO Z X,XIAO Y C,et al. Automatic monitoring system on highway slopes based on GNSS technique[J]. The Chinese Journal of Geological Hazard and Control,2020,31(6):60- 68.(In Chinese)
[115]江胜华,周智,欧进萍.基于磁场梯度定位的边坡变形监测原理[J].岩土工程学报,2012,34(10):1944-1949.
JIANG S H,ZHOU Z,OU J P. Slope deformation monitoring principle based on magnetic gradient tensor[J]. Chinese Journal of Geotechnical Engineering,2012,34(10):1944-1949.(In Chinese)
[116]梁苗,邬凯,邵江,等.LoRa技术在公路边坡监测中的应用研究[J].地下空间与工程学报,2020,16(S2):1011-1016.
LIANG M,WU K,SHAO J,et al. Application study on LoRa technology in highway slope monitoring[J]. Chinese Journal of Underground Space and Engineering,2020,16(S2):1011-1016. (In Chinese)
[117]CHEN Y,WANG S,CHEN N,et al. Forecasting cohesionless soil highway slope displacement using modular neural network[J]. Discrete Dynamics in Nature and Society,2012,2012:504574.
[118]CHENG M Y,HOANG N D. A swarm-optimized fuzzy instancebased learning approach for predicting slope collapses in mountain roads[J]. Knowledge-Based Systems,2015,76:256-263.
[119]CHENG M Y,HOANG N D. Slope corpse prediction using bayesian framework with k-nearest neighbor density estimation:case study in Taiwan[J]. Journal of Computing in Civil Engineering,2016,30(1):1-8.
[120]WANG S,ZHANG Z,REN Y,et al. UAV photogrammetry and AFSA-Elman neural network in slopes displacement monitoring and forecasting[J]. KSCE Journal of Civil Engineering,2019,24 (1):19-29.
[121]YIN C,WANG Z,ZHAO X. Spatial prediction of highway slope disasters based on convolution neural networks[J]. Natural Haz- ards,2022:1-19.
[122]DAS I,STEIN A,KERLE N,et al. Landslide susceptibility mapping along road corridors in the Indian Himalayas using Bayesian logistic regression models [J]. Geomorphology,2012,179:116-125.
[123]黄武彪,丁明涛,王栋,等.基于层数自适应加权卷积神经网络的川藏交通廊道沿线滑坡易发性评价[J].地球科学,2022,47(6):2015-2030.
HUANG W B,DING M T,WANG D,et al. Evaluation of landslide susceptibility based on layer adaptive weighted convolutional neural network model along Sichuan-tibet traffic corridor[J]. Earth Science,2022,47(6):2015-2030.(In Chinese)
[124]鄭志成,徐卫亚,徐飞,等.基于混合核函数PSO-LSSVM的边坡变形预测[J].岩土力学,2012,33(5):1421-1426.
ZHENG Z C,XU W Y,XU F,et al. Forecasting of slope displacement based on PSO-LSSVM with mixed kernel[J]. Rock and Soil Mechanics,2012,33(5):1421-1426.(In Chinese)
[125]GONG W,TIAN S,WANG L,et al. Interval prediction of landslide displacement with dual-output least squares support vector machine and particle swarm optimization algorithms[J]. Acta Geotechnica,2022:1-19.
[126]王志颖,李宗春,许文学.用于边坡变形分析与预测的PSO- Prophet模型[J].岩石力学与工程学报,2021,40(S1):2643-2652.
WANG Z Y,LI Z C,XU W X. PSO-Prophet model for slope deformation analysis and prediction[J]. Chinese Journal of Rock Mechanics and Engineering,2021,40(S1):2643-2652.(In Chinese)
[127]仉文岗,顾鑫,刘汉龙,等.基于贝叶斯更新的非饱和土坡参数概率反演及变形预测[J].岩土力学,2022,43(4):11121122.
ZHANG W G,GU X,LIU H L,et al. Probabilistic back analysisof soil parameters and displacement prediction of unsaturated slopes using Bayesian updating[J]. Rock and Soil Mechanics,2022,43(4):1112-1122.(In Chinese)
[128]LIU C,JIANG Z,HAN X,et al. Slope displacement prediction using sequential intelligent computing algorithms [J]. Measurement,2019,134:634-648.
[129]陈春舒,夏元友.基于极限分析的边坡实时动态Newmark滑块位移法[J].岩石力学与工程学报,2016,35(12):2507-2515.
CHEN C S,XIA Y Y. A real-time dynamic Newmark sliding block method for slopes[J]. Chinese Journal of Rock Mechanics and Engineering,2016,35(12):2507-2515.(In Chinese)
[130]GADE M,NAYEK P S,DHANYA J. A new neural networkbased prediction model for Newmark's sliding displacements [J]. Bulletin of Engineering Geology and the Environment,2020,80 (1):385-397.
[131]NAYEK P S,GADE M. Artificial neural network-based fully data-driven models for prediction of newmark sliding displacement of slopes[J]. Neural Computing and Applications,2022,34 (11):9191-9203.
[132]CHO Y,KHOSRAVIKIA F,RATHJE E M. Acomparison of artificial neural network and classical regression models for earthquake-induced slope displacements[J]. Soil Dynamics and Earthquake Engineering,2022,152:1-12.
[133]HUANG Y,HAN X,ZHAO L. Recurrent neural networks for complicated seismic dynamic response prediction of a slope system [J]. Engineering Geology,2021,289:106198.
[134]WANG M X,HUANG D,WANG G,et al. SS-XGBoost:a machine learning framework for predicting newmark sliding displacements of slopes[J]. Journal of Geotechnical and Geoenvironmental Engineering,2020,146(9):1-17.
[135]MACEDO J,LIU C,SOLEIMANI F. Machine-learning-based predictive models for estimating seismically-induced slope displacements [J]. Soil Dynamics and Earthquake Engineering,2021,148:106795.
[136]陳善静,向朝参,康青,等.基于多源遥感时空谱特征融合的滑坡灾害检测方法[J].计算机研究与发展,2020,57(9):1877-1887.
CHEN S J,XIANG C C,KANG Q,et al. Multi-source remote sensing based accurate landslide detection leveraging spatial- temporal-spectral feature fusion[J]. Journal of Computer Research and Development,2020,57(9):1877-1887.(In Chinese)
[137]GUZZETTI F,REICHENBACH P,ARDIZZONE F,et al. Estimating the quality of landslide susceptibility models[J]. Geomorphology,2006,81(1/2):166-184.
[138]巨袁臻,许强,金时超,等.使用深度学习方法实现黄土滑坡自动识别[J].武汉大学学报(信息科学版),2020,45(11):1747-1755.
JU Y Z,XU Q,JIN S C,et al. Automatic object detection of loess landslide based on deep learning[J]. Geomatics and Information Science of Wuhan University,2020,45(11):1747-1755.(In Chinese)
[139]余加勇,薛现凯,陈昌富,等.基于无人机倾斜摄影的公路边坡三维重建与灾害识别方法[J].中国公路学报,2021,35 (4):77-86.
YU J Y,XUE X K,CHEN C F,et al. Three-dimensional reconstruction and disaster identification of highway slope using unmanned aerial vehicle-based oblique photography technique [J]. China Journal of Highway and Transport,2021,35(4):77-86. (In Chinese)
[140]FENG Q. Measuring fracture orientation at exposed rock faces by using a non-reflector total station [J]. Engineering Geology,2001,59:133-146.
[141]FONSTAD M A,DIETRICH J T,COURVILLE B C,et al. Topographic structure from motion:a new development in photogrammetric measurement [J]. Earth Surface Processes and Landforms,2013,38(4):421-430.
[142]CHEN J,ZHU H,LIX. Automatic extraction of discontinuity orientation from rock mass surface 3D point cloud[J]. Computers and Geosciences,2016,9:18-31.
[143]葛云峰,夏丁,唐辉明,等.基于三维激光扫描技术的岩体结构面智能识别与信息提取[J].岩土力学与工程学报,2017,36 (12):3051-3061.
GE Y F,XIA D,TANG H M,et al. Intelligent identification and extraction of geometric properties of rock discontinuities based on terrestrial laser scanning[J]. Chinese Journal of Rock Mechanics and Engineering,2017,36(12):3051-3061.(In Chinese)
[144]宁浩,董秀军,刘谦,等.利用点云法向量实现岩体结构面识别[J/OL].武汉大学学报(信息科学版):1-13.(2021-10-29)[2022-07-01]. http://kns.cnki.net/kcms/detail/42.1676.tn.20211028.1541.027.html.
NING H,DONG X J,LIU Q,et al. Using point cloud normal vector to realize rock mass structural plane recognition [J/OL]. Geomatics and Information Science of Wuhan University:1-13. (2021-10-29)[2022-07-01].http://kns.cnki.net/kcms/detail/42.1676.tn.20211028.1541.027.html.(In Chinese)
[145]王培涛,覃拓,黄正均,等.基于三维点云的岩体结构面信息快速化识别方法研究[J].岩土力学与工程学报,2021,40 (3):503-519.
WANG PT,QINT,HUANG ZJ,et al. Fast identification of geometric properties of rock discontinuities based on 3D point cloud [J]. Chinese Journal of Rock Mechanics and Engineering,2021,40(3):503-519.(In Chinese)
[146]陈昌富,何旷宇,余加勇,等.基于无人机贴近摄影的高陡边坡结构面识别[J].湖南大学学报(自然科学版),2022,49(1):145-154.
CHEN C F,HE K Y,YU J Y,et al. Identification of discontinuities of high steep slope based on UAV nap-of-the-object photog- raphy[J]. Journal of Hunan University(Natural Sciences),2022,49(1):145-154.(In Chinese)
[147]王鹏宇,王述红.四类常见边坡岩石类别识别和边界范围确定的方法[J].岩土工程学报,2019,41(8):1505-1512.
WANG P Y,WANG S H. Method for identifying four common rock types of slopes and determining boundary range[J]. Chinese Journal of Geotechnical Engineering,2019,41(8):1505-1512. (In Chinese)
[148]张紫杉,王述红,王鹏宇,等.岩坡坡面裂隙网络智能识别与参数提取[J].岩土工程学报,2021,43(12):2240-2248.
ZHANG Z S,WANG S H,WANG P Y,et al. Intelligent identification and extraction of geometric parameters for surface fracture networks of rocky slopes[J]. Chinese Journal of Geotechnical En- gineering,2021,43(12):2240-2248.(In Chinese)
[149]漆祖芳,姜清輝,周创兵,等.基于lSVR和MVPSO算法的边坡位移反分析方法及其应用[J].岩石力学与工程学报,2013,32(6):1185-1196.
QI Z F,JIANG Q H,ZHOU C B,et al. A new slope displacement back analysis method based on v-SVR and MVPSO algorithm and its application[J]. Chinese Journal of Rock Mechanics and Engi- neering,2013,32(6):1185-1196.(In Chinese)
[150]LIU Y,REN W,LIU C,et al. Displacement-based back- analysis frameworks for soil parameters of a slope:using Frequentist inference and Bayesian inference[J]. International Journal of Geomechanics,2022,22(4):04022026.
[151]ZHANG L L,ZUO Z B,YE G L,et al. Probabilistic parameter estimation and predictive uncertainty based on field measurements for unsaturated soil slope[J]. Computers and Geotechnics,2013,48:72-81.
[152]WANG L,HWANG J H,LUO Z,et al. Probabilistic back analysis of slope failure-A case study in Taiwan[J]. Computers and Geotechnics,2013,51:12-23.
[153]LI S,ZHAO H,RU Z,et al. Probabilistic back analysis based on Bayesian and multi-output support vector machine for a high cut rock slope[J]. Engineering Geology,2015,203:178-190.
[154]JIANG S H,HUANG J,QI X H,et al. Efficient probabilistic back analysis of spatially varying soil parameters for slope reliability assessment[J]. Engineering Geology,2020,271:105597.
[155]江巍,歐阳晔,闫金洲,等.边坡岩土体抗剪强度的逆向迭代修正反演方法[J].岩土力学,2022,43(8):1-9.
JIANG W,OUYANG Y,YAN J Z,et al. Inversion iterative correction method for estimating shear strength of rock and soil mass in slope engineering[J]. Rock and Soil Mechanics,2022,43(8):1-9.(In Chinese)
[156]LIU X,WANG Y. Bayesian selection of slope hydraulic model and identification of model parameters using monitoring data and subset simulation[J]. Computers and Geotechnics,2021,139:104428.

