三阶非线性效应对边界限制的自聚焦振荡型响应函数系统中二次孤子的影响*
陈娟 胡巍 陆大全
1)(江西师范大学物理与通信电子学院,南昌 330022)
2)(华南师范大学,广东省微纳光子功能材料与器件重点实验室,广州 510631)
面向边界限制的自聚焦振荡型响应函数系统建立了二阶和三阶非线性共同作用时的二次孤子理论模型.在此基础上,通过数值模拟对有三阶非线性效应和无三阶非线性效应情况下的孤子解进行对比,研究了三阶非线性效应对该系统中二次孤子的影响.结果表明,在孤子波形方面,三阶非线性影响较小,仅轻微改变其横向分布.但是在孤子的存在区间方面,三阶非线性导致孤子只存在于强非局域和一般非局域情况,在弱非局域情况下找不到相应的孤子.此外,三阶非线性的存在还减少了孤子拓展半周期的个数.而在孤子稳定性方面,三阶非线性则缩减了孤子的稳定区间.
1 引言
光孤子是指光波在非线性介质中发生自陷的稳定传输现象,包括时间光孤子、空间光孤子以及时空光孤子[1,2].近年来,非局域非线性介质中的光孤子(非局域孤子)引起了研究人员的广泛关注[3-8].非局域非线性介质的非线性折射率与该点及其附近的光场均有关.根据介质非局域响应函数特征宽度与光束束宽的相对大小,通常将非局域程度细分为强非局域、一般非局域、弱非局域以及局域4 种类型[1,9,10].非局域孤子涉及的传输介质主要包括向列相液晶[4,11-13]、铅玻璃[14,15]及二次非线性介质[16-19].值得一提的是,二次非线性介质中的孤子(二次孤子)尽管在1974 年就已经被理论预言[20],并且在此后数十年里得到了诸多的研究[17,21-23],但是起初研究人员并没有将其与非局域非线性联系起来.直到 2003 年,Nikolov 等[16]发现二次孤子可以等价于非局域孤子,二次谐波(SH)可以看作是由基频波(FW)诱导的等价非局域非线性折射率,它会形成一个非线性波导并在二次参量过程中限制基频波的传输.在此基础上,研究人员发现二次非线性介质中存在指数衰减型和正弦振荡型两种非局域响应函数[16].在指数衰减型响应函数系统中的二次孤子易于稳定[17,21,24,25],而正弦振荡型响应函数系统中的二次孤子则很难稳定[22,26].
近年来,本课题组对振荡型响应函数系统中的二次孤子进行了一系列的研究.2014 年,我们通过引入边界约束得到了自聚焦的振荡型响应函数系统中可稳定传输的孤子解[27,28].2017 年,我们进一步在边界约束的自散焦振荡型响应函数系统中找到了亮的二次孤子[29].2018 年,我们还在无边界的自聚焦振荡型响应函数系统下发现了暗-亮孤子对[30].与之前二次孤子的大多数研究工作一样,在上述工作中只考虑了二阶非线性效应这一主要非线性.但是实际上,当光在二次非线性介质中传输时,还会存在三阶非线性效应.尽管三阶非线性效应比二阶非线性效应要弱很多,但是对于孤子不易稳定的振荡型响应函数系统而言,其对孤子的存在区间和稳定性等方面仍有可能构成较明显的影响.
针对这一问题,本文面向边界限制的自聚焦振荡型响应函数系统建立二阶和三阶非线性共同作用时的二次孤子理论模型.在此基础上,通过数值模拟对有三阶非线性效应和无三阶非线性效应情况下的孤子解进行对比,系统地研究三阶非线性效应对孤子波形、孤子存在区间、以及孤子稳定性三个方面的影响.
2 理论模型
二阶和三阶非线性效应共同作用时,孤子传输满足耦合方程组[22,26,31]:

式中,E1和E2分别表示基频波和二次谐波光电场的复振幅;ω1和ω2=2ω1分别为基频波和二次谐波的频率;k1=n1ω1/c和k2=n2ω2/c分别为基频波和二次谐波的波数,其中n1和n2分别为介质对基频波和二次谐波的折射率; Δk=2k1-k2为相位失配量;分别为二阶和三阶有效非线性极化率.方程(1)和方程(2)的第一项代表传输,第二项代表衍射或群速度色散,第三项代表二阶非线性效应,最后一项代表三阶非线性效应.
对方程(1)和方程(2)引入下面一组变换参数:
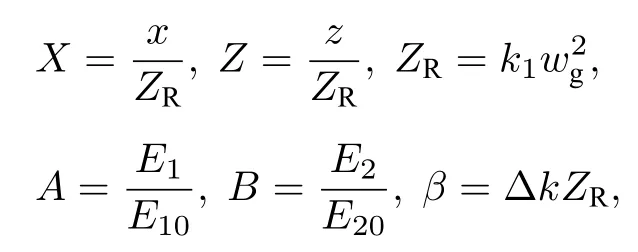
其中wg>0 为光束束宽或脉冲宽度,ZR=>0 为光束的瑞利距离或色散距离,E10和E20为归一化常数.可得无量纲传输方程组:

其中s1的符号决定了系统的非线性是自聚焦的(s1=1)还是自散焦的(s1=-1).在不考虑三阶非线性效应时(即n=0 时),上述孤子模型可以等价为非局域孤子的传输模型[16],二次谐波可视为由基频波诱导的等价非局域非线性折射率.因此,二次谐波可以表示为基频波与响应函数的卷积形式,即
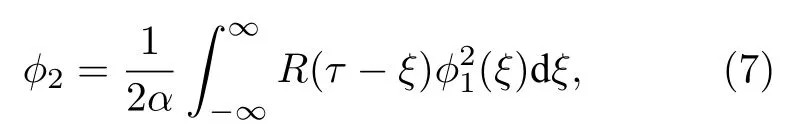
其中R(·)代表响应函数.当s2=1 时,响应函数为指数衰减型,即
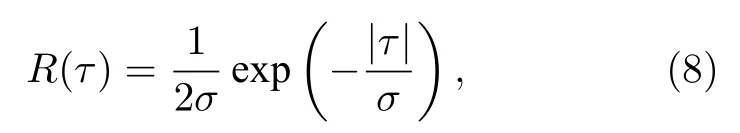
其中σ=.而对于s2=-1 情况,当系统无边界条件约束时响应函数为正弦振荡型,即
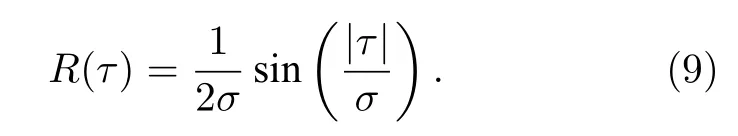
但在有界系统中(设两边界分别位于l1和l2,介质宽度为l=l2-l1),当边界两边的折射率差足够大时(如二次介质样品放置于空气中),光场主要集中于介质内.此时的边界条件近似满足第一类边界条件(即φ1,2(l1)=φ1,2(l2)=0),相应的响应函数为[27,28]
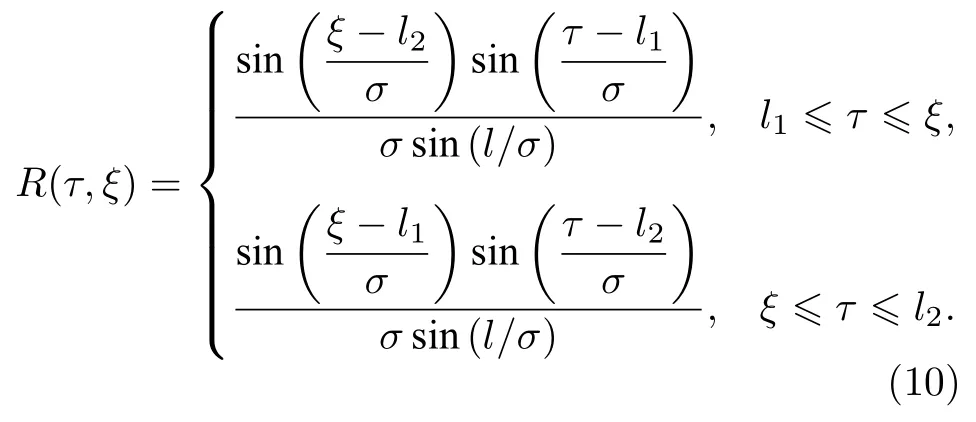
由(8)-(10)式可见,非局域响应函数的特征宽度可用参量σ=来表示.通常用非局域响应函数特征宽度σ与光束束宽的比值大小来衡量非局域程度.因此,α的值越小,特征宽度σ就越大,非局域程度就越强.如果将非局域程度作粗略的分类,通常把比值远小于1 的情况称为弱非局域;把比值与1 可比拟的情况称为一般非局域;把比值远大于1 的情况称为强非局域.
接下来基于方程(5)和方程(6)的模型,研究三阶非线性效应对边界限制的自聚焦振荡型响应函数系统中(即s1=-s2=1)二次孤子的影响.孤子的数值求解采用牛顿迭代法.此外,为了判断孤子的稳定性,对通过牛顿迭代法得到的孤子解进行线性稳定性分析.对基波和二次谐波的试探孤子解都加入微扰:
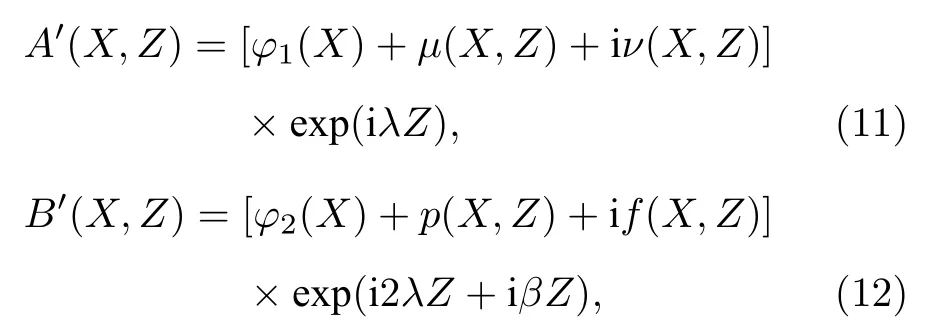
其中µ,ν,p,f都为实数,且µ,ν,p,f≪1 .将微扰解代入方程(3)和方程(4),可得一个实矩阵b=(µ,ν,p,f)T的特征值问题:

其中

而
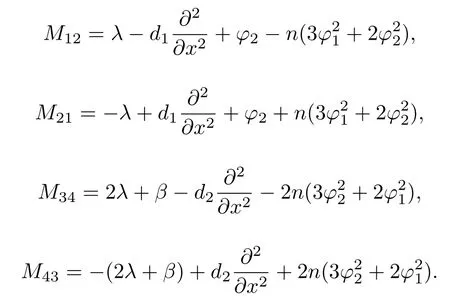
在第一类边界条件下,利用中心差分法离散化求解特征方程的特征值ε.ε的实部(εr)表示不稳定增长率,若εr≤0 则孤子稳定,反之则不稳定.
3 数值模拟结果与分析
基于二阶和三阶非线性效应共同作用时的孤子模型,研究了该模型下的孤子波形、存在区间以及稳定性.下面详细地讨论三阶非线性效应对这三方面的影响.
在强非局域和一般非局域情况下,找到了一系列的孤子解,它们的波形如图1 所示.可以看到,二阶和三阶非线性共同作用下的孤子波形与只有二阶非线性作用时的二次孤子波形很接近.具体而言,在强非局域条件下基频波呈钟型分布,二次谐波呈正弦振荡型周期分布,如图1(a)和图1(b)所示.在一般非局域条件下,基频波存在两种波形,其中一种波形存在一些肩膀,具有格子孤子的特点,第二种波形平滑流畅,如图1(c)和图1(d)所示.

图1 强非局域和一般非局域情况下二阶和三阶非线性共同作用时的孤子波形(红色: 基频波;绿色: 二次谐波)(a),(b)强非局域情况 α=0.04,其中图(b)的波形是在图(a)的基础上向两边各拓展了半个周期;(c),(d)一般非局域情况 α=10,其中图(c)中 l=18.0974,图(d)中 l=18.7214 .图中虚线为二阶和三阶非线性共同作用时的孤子波形;实线为只有二阶非线性作用时的二次孤子波形;|d2/d1|=1Fig.1.Soliton profiles(red: FW;green: SH)with quadratic and cubic nonlinearities for strongly nonlocal case and general nonlocal case:(a),(b)Strongly nonlocal case α=0.04 ;the soliton in panel(b)is an extension of that in panel(a)toward the right and left sides;(c),(d)general nonlocal case α=10 ,where(c)l=18.0974,(d)l=18.7214 .Dotted line: soliton profiles with quadratic and cubic nonlinearities;Solid line: the profiles of quadratic solitons with only quadratic nonlinearity. |d2/d1|=1.
但是在弱非局域条件下发现,当三阶非线性系数n在10-3—10-1范围内时,无论|d2/d1|取何值都不存在对应的孤子解.也就是说,三阶非线性效应的存在使得在此情况下找不到对应的孤子.我们也尝试了在更弱的三阶非线性系数条件下去寻找孤子解,但是直到当n取10-6时,方程才出现了孤子解.然而此时n~10-6量级相对于二阶非线性效应来说,三阶非线性的作用就是一个极小的微扰量,结果与仅有二阶非线性情况并无实质区别,因此无意义.所以在本文后续的讨论中,只考虑强非局域和一般非局域的情况,并取三阶非线性系数n=0.003.
图2 所示为孤子基频波的束宽和功率随样品宽度l的变化情况,其中功率和束宽分别为
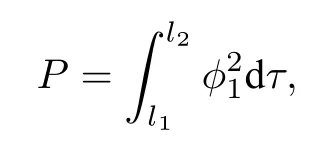

从图2 可以看出,二阶和三阶非线性共同作用时的变化规律与只有二阶非线性作用时的规律基本一致,都是呈现周期性的分段变化.区别主要在于,考虑了三阶非线性效应后,其变化曲线在无三阶非线性效应情况的对应曲线基础上向右发生了偏移.但值得注意的是,图2 中第2,3 支的束宽和功率是在第1 支的基础上对样品宽度分别拓展半个周期和一个周期所得.在对孤子进行拓展的过程中,可以发现三阶非线性的存在减少了孤子可拓展半周期的个数,如图2(a)最多只能拓展半个周期.
图3 是不稳定增长率随样品宽度l、非局域程度α、以及比值d2/d1的变化.对于不稳定增长率随样品宽度l的变化情况而言(图3(a)和图3(b),与图2 对应),可以发现,考虑了三阶非线性效应的孤子其不稳定增长率曲线在只有二阶非线性作用时曲线的基础上也向右发生了偏移.另外,通过与只有二阶非线性作用时的二次孤子稳定性区间对比还发现,三阶非线性效应的存在缩减了孤子的稳定区间,如图3(c)和图3(d)所示.

图2 基频波的束宽(蓝色)和功率(红色)随样品宽度l 的变化规律(a)强非局域情况 α=0.04;(b)一般非局域情况 α=10 .虚线为二阶和三阶非线性共同作用时的结果;实线为只有二阶非线性作用时的结果.|d2/d1|=0.8Fig.2.Soliton width(blue line,right ordinate)and power(red line,left ordinate)of the FW versus the sample size l:(a)Strongly nonlocal case α=0.04;(b)general nonlocal case α=10 .Dotted line: results with quadratic and cubic nonlinearities;Solid line:results with only quadratic nonlinearity. |d2/d1|=0.8 .
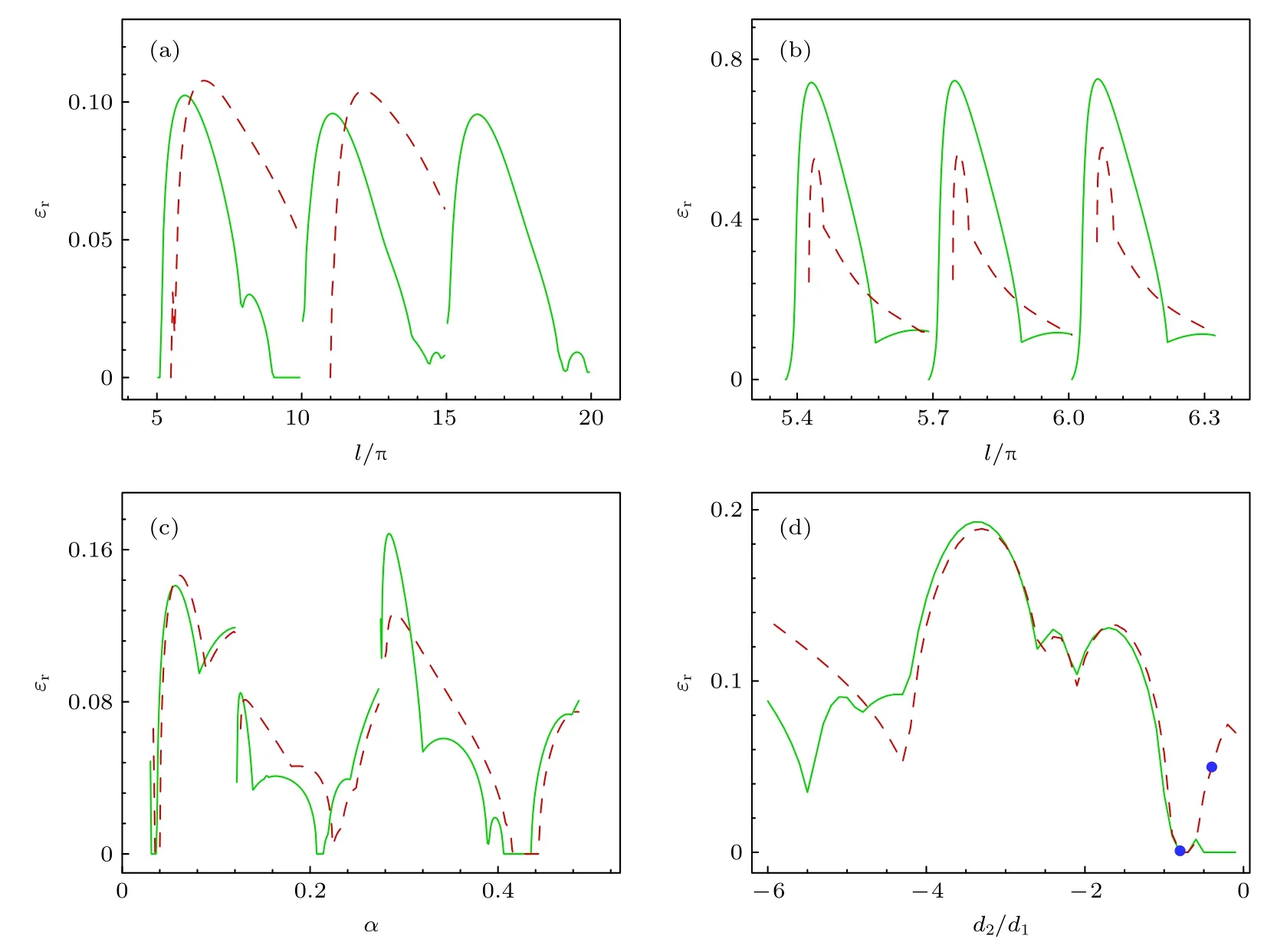
图3 (a),(b)对应图2 的孤子不稳定增长率曲线;(c)孤子的不稳定增长率随非局域程度α 的变化规律,l=18 ,|d2/d1|=2 ;(d)孤子的不稳定增长率随 d2/d1 的变化规律,α=0.11,l=18 .虚线为二阶和三阶非线性共同作用时的结果;实线为只有二阶非线性作用时的结果Fig.3.(a),(b)Curves of unstable growth rate corresponding to Fig.2;(c)unstable growth rate versus the nonlocal degree α.l=18,|d2/d1|=2;(d)unstable growth rate versus d2/d1 .α=0.11,l=18 .Dotted line: results with quadratic and cubic nonlinearities;Solid line: results with only quadratic nonlinearity.
图4 所示为图3(d)中两个圆点所对应孤子解的数值模拟传输结果.将牛顿迭代法得到的孤子解作为初始输入,基于方程(3)和方程(4)采用分步傅里叶算法对其进行了传输模拟.在传输模拟时给预期稳定的孤子解中的基频波加入了1%的微扰,而预期不稳定的孤子解则不加微扰.从图4 可以观察到,预期稳定的孤子解经过1000 个瑞利距离ZR的传输后,孤子仍然能保持稳定,而预期不稳定的孤子解仅仅经过几十个瑞利距离后就再也不能稳定传输下去.

图4 图3(d)中两个圆点所对应孤子解的数值模拟传输结果(a),(b)基频波;(c),(d)二次谐波.第一行中 d2/d1=-0.8 ;第二行中d2/d1=-0.4Fig.4.Propagation of the two solitons corresponding to the two dots in Fig.3(d):(a),(b)The FW;(c),(d)the SH.Upper row:d2/d1=-0.8;Bottom row: d2/d1=-0.4 .
4 结论
本文系统研究了三阶非线性效应对边界限制的自聚焦振荡型响应函数系统(s1=-s2=1)中二次孤子的影响.发现考虑了三阶非线性作用后,孤子只存在于强非局域和一般非局域情况,弱非局域情况下找不到相应的孤子(过去忽略三阶非线性作用时在各类非局域程度下都存在孤子解).此外还发现,三阶非线性效应的存在减少了孤子拓展半周期的个数,同时也缩减了孤子的稳定区间.而在孤子波形方面,三阶非线性影响较小,仅轻微改变其横向分布.
感谢东莞理工学院陈曼娜博士的有益讨论.

