基于标记相关性和ReliefF的多标记特征选择
孙 林,杜雯娟,李 硕,徐久成
(河南师范大学 计算机与信息工程学院,河南 新乡 453007)
多标记学习是目前机器学习和数据挖掘等领域中的热门研究方向之一[1]。目前,维度灾难问题已成为多标记学习的重要挑战之一[2]。特征选择无需进行映射变换即可从原始特征空间中选择出重要特征信息,且保留原始数据的分类能力,有效地降低了数据的特征维度[3-5]。互信息在信息论中用于衡量两个随机变量之间的相关程度,通常用于统计语言模型中计算特征与特征之间的关系[6-7]。互信息可以认为是一个随机变量由于另一个已知随机变量而减少的不确定性[8-9]。由于互信息无需对特征与标记之间关系的性质作出假设,因此非常适合于多标记学习任务。Sun等[10]提出了一种基于邻域互信息的多标记特征选择算法。但是,该算法的输出结果是随机的,这会导致权重值的波动,同时杰卡德相关系数受稀疏标记矩阵的影响,容易导致计算结果的不平衡。Huang等[11]利用最大相关最小冗余设计了一种基于邻域粗糙集模型的多标记特征选择算法。然而,该算法只考虑了单个标记中的样本邻域半径,忽略了标记之间的相关性。Wang等[12]结合Fisher分数和邻域粗糙集提出了一种新的多标记特征选择算法。然而,该算法忽略了特征之间的相关性且未考虑多标记高阶相关性,导致计算复杂度偏高。Lim等[6]利用互信息提出了基于进化算法的多标记特征选择方法。但是,该方法在计算时间上开销较大。Huang等[2]利用流形正则化和依赖最大化提出了一种多标记特征选择算法。但是,该算法没有考虑标记相关性,计算复杂度较高。Wang等[13]提出了一种基于互信息和谱粒度的多标记在线流特征选择算法。然而当信息粒数变大时,其计算复杂度可能会大大增加。基于上述研究的启发,综合考虑特征与标记集之间的互信息,结合标记权重来定义标记相关性公式,对多标记数据集进行预处理,初步筛选出与标记集合相关度较高的特征子集。
Relief算法是一种过滤式特征选择方法[14],该算法赋予每个特征不同的权重,权重小于某个阈值的特征将被剔除。Kira等[15]提出的Relief算法只能用于二分类问题。为了研究适用于多标记分类问题的ReliefF算法,蔡亚萍等[16]提出了一种结合局部相关性的多标记ReliefF特征选择算法。刘海洋等[17]利用ReliefF算法度量标记间的依赖关系,选择有较强依赖关系的标记加入原始特征空间。但是,上述算法均未考虑特征与标记的相关性。马晶莹等[18]通过研究最近的同类样本和异类样本的搜索方法,提出基于多标记ReliefF的特征选择算法。然而,该算法确定随机样本的最近邻样本数较少,容易导致特征权重值波动较大。Kong等[19]基于ReliefF和F-statistic研究了特征选择算法,并将其应用在多标记图像标注任务中。但上述方法没有考虑不同标记对于样本数据具有不同的可分性。林梦雷等[20]计算样本在特征上的欧式距离并对标记进行加权,提出了基于加权标记的多标记特征选择算法。但是,当样本间的距离非常大时会使异类样本或者同类样本无效。为了解决这个问题,引入异类样本和同类样本数量,结合特征与标记集合相关度构建一种新的特征权重更新公式,消除样本距离过大时带来的负面影响,进而设计了带有标记权重的多标记ReliefF算法。其主要贡献如下:
1) 为了解决没有充分考虑特征与标记之间的相关性而造成分类精度偏低的问题,使用特征与标记集合的互信息和改进的标记权重,定义标记相关性公式,衡量特征与标记之间的相关程度,初步筛选出与标记集相关度较高的特征子集。
2) 为了解决传统ReliefF算法会因样本间距离过大,导致异类样本和同类样本失去原有度量特征重要性的作用,引入异类样本数和同类样本数消除样本间距过大的影响,由此分别计算样本与最近邻样本间的距离;结合标记权重构建新的特征权值更新公式,进而选择初筛特征集合中的重要特征。
3) 为了解决传统ReliefF算法分类精度偏低的问题,构建基于标记相关性和改进ReliefF算法的多标记特征选择算法,提高多标记数据的分类性能。
1 基础理论
1.1 熵与互信息
假设MLDS=〈U,C,D,T〉是一个多标记决策系统,其中U={x1,x2,…,xn}表示由n个样本构成的样本集;C表示特征属性集,D表示各个样本对应的标记空间,L表示标记总个数;T={(xi,yi)|i=1,2,…,n}表示在标记上的映射关系。每个样本由f维表示,记为xi∈Rf,对应的标记集由向量yi∈{0, 1}l表示,其中l∈D。如果xi有l类别标记,则yi(l)=1,否则yi(l)=0;且∑yi≥ 1。
在MLDS=〈U,C,D,T〉中,对任意的xi∈X⊆U(i=1, 2, …,n),p(xi)为样本xi的先验概率,则集合X的信息熵[10-11]表示为
(1)
在MLDS=〈U,C,D,T〉中,任意两个样本子集X、Y⊆U,xi∈X和yj∈Y(i,j=1, 2, …,n),p(xi,yj)为两个样本xi和yj的先验概率,则X和Y的联合信息熵[10]表示为
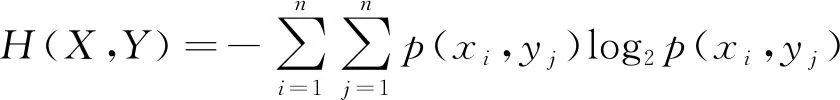
(2)
在MLDS=〈U,C,D,T〉中,X、Y⊆U,xi∈X和yj∈Y(i,j=1, 2, …,n),p(yj|xi)为条件先验概率,则Y在给定X下的条件熵[10]表示为

(3)
X和Y的互信息量表示已知Y的条件下,X不确定性的改变量,从统计学角度反映了X和Y的关联程度,所以X和Y的互信息[13]表示为

(4)
易证明0 ≤I(X;Y)≤1。I(X;Y)=0表示X和Y相互独立,I(X;Y)=1表示X和Y之间相关性较强。
1.2 大间隔
在MLDS=〈U,C,D,T〉中,对于任意的X⊆U,xi∈X(i=1, 2, …,n),则样本xi的分类间隔[20]表示为
margin(xi)=Δ(xi,NM(xi))-
Δ(xi,NH(xi))
(5)
其中:NM(xi)是在样本空间U中与xi距离最近的异类样本,称为xi的最近邻异类样本;NH(xi)是在样本空间U中与xi距离最近的同类样本,称为xi的最近邻同类样本;Δ(xi, NM(xi))和Δ(xi, NH(xi))分别代表xi到NM(xi)和NH(xi)的距离。
在MLDS=〈U,C,D,T〉中,特征空间F⊆C,fj∈F(j=1, 2,…,z),对于任意的X⊆U,xi∈X(i=1, 2, …,n),则第i个特征的权重可被计算[20]为
wi=wi+|xi-NM(xi)|-|xi-NH(xi)|
(6)
其中:|xi-NM(xi)|-|xi-NH(xi)|表示样本在第i个特征分量上的间隔的2倍。
2 多标记特征选择方法
2.1 特征和标记集之间的相关度
为解决部分方法忽略特征和标记之间的相关度而造成分类精度偏低且时间代价较大的问题,引入标记权重的概念,并将其与传统互信息相结合,更精确地反映特征与标记集的相关度,从而提高算法的分类精度。
定义1在MLDS=〈U,C,D,T〉中,任意标记子集L⊆D,标记lk∈L,其中k=1, 2, …,m,则标记lk的权重定义如下

(7)
其中:n是样本数;n(lk)表示含有标记lk的正类样本数;W(lk)反映正类样本在标记集合中所占的比例。
定义2在MLDS=〈U,C,D,T〉中,F⊆C,fj∈F(j=1, 2, …,z),L⊆D,lk∈L(k=1, 2, …,m), 每个特征和标记集之间的相关度计算公式为

(8)
其中:I(f;lk)表示特征与标记之间的互信息;W(lk)为定义1中的标记权重。结合标记集合中正类样本的分布情况,为标记赋予不同的权重,动态地调节特征f与标记集L的相关程度。由此可知,特征与标记集合的相关度可用特征与标记集合间各个标记的互信息与标记权重的乘积的总和来衡量。
2.2 改进的多标记ReliefF
为了解决原有的ReliefF方法会因样本间距离过大,导致异类样本和同类样本失去原有度量特征重要性的作用,引入异类样本和同类样本数量来消除该影响,并结合定义1的标记权重公式,改进多标记ReliefF模型,进而构建新的特征权值更新公式,有效提高了算法的分类性能。
定义3在MLDS=〈U,C,D,T〉中,X⊆U,xi∈X(i=1, 2, …,n),F⊆C,fj∈F(j=1, 2, …,z), 对任意的特征f∈F,任意两个样本xi和xj在特征f上的距离公式表示为

(9)
其中:xi(f)表示xi在f上的值;xj(f)表示xj在f上的值;max(f)和min(f)分别表示特征f在样本空间中取得的最大值和最小值。
定义4在MLDS=〈U,C,D,T〉中,X⊆U,xi∈X(i=1, 2, …,n),F⊆C,fj∈F(j=1, 2, …,z),L⊆D,lk∈L(k=1, 2, …,m), 则样本xi分类间隔定义为

(10)
其中:NMl(xi)表示标记l中xi的最近邻异类样本;NHl(xi)表示标记l中xi的最近邻同类样本;df(xi, NMl(xi))表示在特征f下样本xi在标记l中与其最近邻异类样本的距离,df(xi, NHl(xi))表示在特征f下样本xi在标记l中与其最近邻同类样本的距离;|NNM|和|NNH|分别表示异类样本数量和同类样本数量。
定义5在MLDS=〈U,C,D,T〉中,X⊆U,xi∈X(i=1, 2, …,n),F⊆C,fj∈F(j=1, 2, …,z),L⊆D,lk∈L(k=1, 2, …,m), 结合标记权重和样本分类间隔定义特征权值更新公式为

(11)
其中:W(lk)为标记权重;CM(xi)表示xi的分类间隔。
2.3 算法描述
首先,计算标记所占的比例权重,得到标记权重;其次,计算每个特征和标记集之间的相关度,根据相关度的值初次筛选出特征子集;然后,根据式(11)得出特征权重值;最后,根据特征重要性权值选出最终特征排序。由此,设计基于互信息的标记相关性并结合基于标记权重的ReliefF的多标记特征选择(mutual information-based label correlation and label weighting-based ReliefF, MI-LW)算法,其伪代码如下:
算法1MI-LW算法
输入 MLDS=〈U,C,D,T〉
输出 最优选特征子集S
/*初步筛选模块*/
Step1 For eachl∈D
Step2 For eachf∈C
Step3 由式(4)计算标记和特征之间的互信息
Step4 End For
Step5 End For
Step6 For eachlk∈D
Step7 根据式(7)计算含有标记lk的正类样本个数并得出标记权重W(lk)
Step8 End For
Step9 For eachf∈C
Step10 For eachl∈D
Step11 根据式(8)计算CFL(f,D)
Step12 End For
Step13 End For
Step14 根据CFL值初次筛选出特征子集S-temp
/*Multi-Label-ReliefF模块*/
Step15 For eachxi∈U
Step16 计算xi的NMl(xi)和NHl(xi)
Step17 End For
Step18 对标记权重W(lk)归一化
Step19 For eachf∈C
Step20 For eachxi∈U
Step21 根据式(11)逐个计算特征f的权重Wf
Step22 End For
Step23 End For
Step24 根据Wf值对特征进行排序,输出前k个特征组成最终的特征子集S
在MI-LW算法中,假设多标记数据集包括n个样本、m个标记和z个特征。Step1至Step5计算标记和特征之间互信息的复杂度为O(mz),Step6到Step8计算标记权重的复杂度为O(m),Step9至Step13计算特征和标记集之间的相关度,复杂度为O(mz),Step15到Step17计算xi的最近邻异类样本NMl(xi)和最近邻同类样本NHl(xi),复杂度为O(n),Step18对标记权重归一化,复杂度为O(1),Step19至Step23计算特征权重的复杂度为O(mz),其中Step14和Step24为特征排序和输出特征子集,时间复杂度均为O(zlogz)。由此,计算MI-LW算法总的时间复杂度为O(mz+m+n+zlogz)。
3 实验结果及分析
3.1 实验准备
实验环境为Matlab R2019a,实验使用计算机系统为Windows 7的64位操作系统、处理器为Intel(R)Core(TM)i7-4790 CPU @ 3.60GHz、内存为8GB。采用多标记k最近邻方法[20](Multi-labelk-nearest neighbors,ML-KNN)作为分类器来评估所提算法的性能,设置本实验中的近邻个数为10,平滑系数调节为1。为验证MI-LW算法的有效性,在Mulan数据库中选取7个数据集进行实验(http:∥mulan.sourceforge.net/datasets.html),详细信息描述如表1所示。为了评估所提算法的分类性能,采用文献[10]中的5个指标:平均分类精度(Average Precision, AP)、覆盖率(Coverage, CV)、1-错误率(One Error, OE)、排序损失(Ranking Loss, RL)、汉明损失(Hamming Loss, HL),并结合所选特征个数(the Number of Selected Features,NF)进行比较。在下面实验结果中,“↑”表示值越大分类性能越好,“↓”表示值越小分类性能越好;表格中的粗体均表示最优结果。

表1 7个多标记数据集描述
3.2 ML-KNN下的实验结果
在第一部分实验中采用消融实验来证明MI-LW算法的有效性,选择5个指标:AP、CV、HL、RL和OE进行评估。ReliefF表示原始ReliefF,Cor表示原始相关度,I-ReliefF表示改进的RelieF,I-Cor表示改进的相关度,MI-LW表示改进ReliefF和改进相关度相结合。在表1中选择7个数据集作为实验数据集。表2给出了4种多标记特征选择方法在7个多标记数据集上的分类结果。
从表2中可以看出,在AP指标上,MI-LW算法在Emotions、Education、Social、Yeast、Flags和Arts这6个数据集上均取得最优;在Health数据集上,MI-LW算法为次优,与ReliefF+I-Cor持平,比ReliefF高了0.063 3。在CV指标上,MI-LW算法在Emotions、Health、Yeast和Flags这4个数据集上均取得最优;在Education数据集上,MI-LW算法为次优,与ReliefF+I-Cor持平,比ReliefF低了0.328 3;在Social数据集上,MI-LW算法为次优,与ReliefF+I-Cor持平,比ReliefF低了0.192;在Arts数据集上,MI-LW算法为次优,与ReliefF+I-Cor持平,比ReliefF低了0.263 7。在HL指标下,MI-LW算法在Education、Health、Social和Arts这4个数据集上均取得最优;在Emotions数据集上,MI-LW算法比ReliefF低了0.033 8;在Yeast数据集上, MI-LW算法比ReliefF低了0.004 6;在Flags数据集上,MI-LW算法为次优,与ReliefF+I-Cor持平,比ReliefF低了0.028 6。在RL指标上,MI-LW算法在Emotions、Social、Yeast和Flags这4个数据集上均取得最优;在Education数据集上,MI-LW算法为次优,与ReliefF+I-Cor持平,比ReliefF低了0.01;在Health数据集上,MI-LW算法为次优,与ReliefF+I-Cor持平,比ReliefF低了0.008 5;在Arts数据集上,MI-LW算法为次优,与ReliefF+I-Cor持平,比ReliefF低了0.012。在OE指标上,MI-LW算法在Emotions、Education、Social和Arts这4个数据集上均取得最优;在Health数据集上,MI-LW算法为次优,与ReliefF+I-Cor持平,比ReliefF低了0.100 3;在Yeast数据集上,MI-LW算法为次优,与ReliefF+I-Cor持平,比ReliefF低了0.090 4;在Flags数据集上,MI-LW算法仅比最优ReliefF高了0.015 4,与其他2种算法持平。综上分析,MI-LW算法优于ReliefF、ReliefF+I-Cor和I-ReliefF+Cor,该实验充分验证了MI-LW算法的有效性。
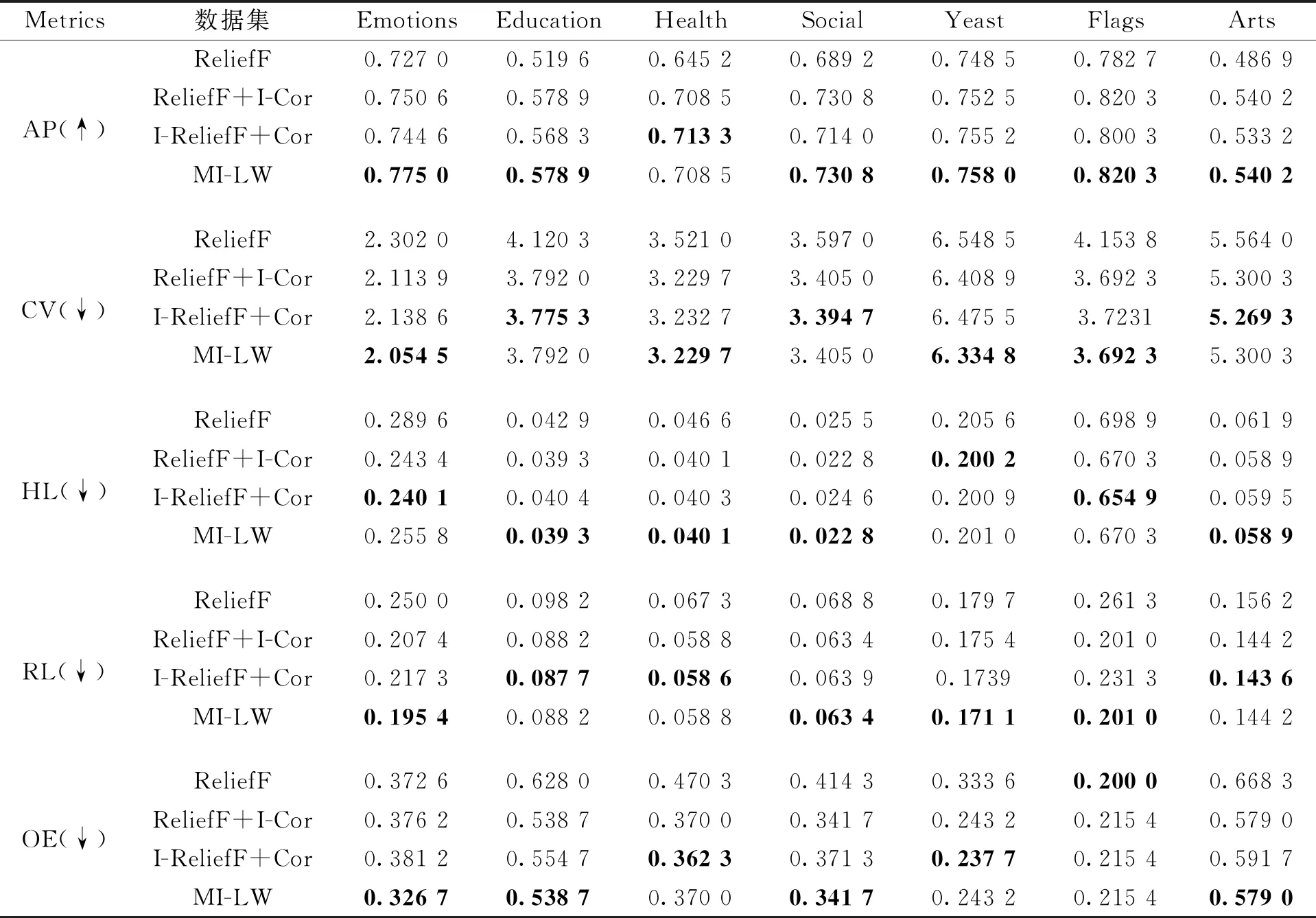
表2 MI-LW在7个数据集上的消融实验结果
在第二部分实验中,选择4个指标(AP、RL、OE和CV)进行算法评估,对比算法包括基于最大相关性的多标记维数约简算法(multi-label dimensionality reduction algorithm via dependence maximization, MDDM)[21],其中,MDDM按照参数的不同可以分为MDDMspc和MDDMproj、基于多变量互信息的多标记特征选择算法(feature selection algorithm for multilabel classification using multivariate mutual information, PMU)[22]、多标记朴素贝叶斯分类的特征选择算法(feature selection algorithm for multi-label naïve Bayes classification, MLNB)[23]、基于标记相关性的多标记特征选择算法(multi-label feature selection algorithm with label correlation, MUCO)[13]、基于邻域粗糙集和Relief的弱标记特征选择算法(weak label feature selection algorithm based on neighborhood rough sets and relief, WFSNR)[1]和基于AP聚类和互信息的弱标记特征选择算法(weak label feature selection algorithm based on AP clustering and mutual information,WFSAM)[24]。从表1中选择4个数据集作为实验数据集。表3给出了8种算法在4个多标记数据集上4个指标的分类结果。
从表3中可以看出,在AP指标上,MI-LW算法在Health、Yeast和Flags这3个数据集上均为最优;在Emotions数据集上,MI-LW算法为次优,仅比最优算法MUCO低了0.000 5,但比其他对比算法高了0.001 6~0.066 9。在RL指标上,MI-LW算法在Health、Yeast和Flags这3个数据集上均为最优;在Emotions数据集上,MI-LW算法的RL值仅比最优MDDMspc算法高了0.019 2,但比PMU、MLNB、WFSNR和WFSAM这4种算法分别低0.070 2、0.010 1、0.019 8和0.039 4,与MDDMproj算法基本持平。在OE指标上,MI-LW算法在Health和Flags这2个数据集上均为最优;在Emotions数据集上,MI-LW算法的OE值仅比最优算法MUCO高了0.009 9,但比MDDMproj算法低了0.024 8,比PMU算法低了0.064 4,比MLNB算法低了0.049 8,比WFSNR算法低了0.054 5,比WFSAM算法低了0.059 4,与MDDMspc算法基本持平;在Yeast数据集上,MI-LW算法的OE值仅比最优算法PMU高了0.010 1,但比MDDMspc算法低了0.016 1,比MDDMproj算法低了0.009 5,比MLNB算法低了0.012 8,比MUCO算法低了0.009 5,与WFSAM算法持平。在CV指标上,MI-LW算法在Health、Yeast和Flags这3个数据集上均为最优;在Emotions数据集上,MI-LW算法的CV值仅比最优算法MDDMspc高了0.109 0,但比PMU、MLNB、WFSNR和WFSAM这 4种算法分别低了0.351 4、0.019 8、0.089 1和0.232 6,与MDDMproj算法基本持平。对于Emotions数据集,MI-LW算法在4个指标上均未取得最优,Emotions数据集的标记集为稀疏矩阵,且标记分布也较为集中,导致MI-LW算法在Emotions数据集上性能不佳。

表3 4个数据集上8种算法的4个指标对比结果
第三部分实验选择在不同特征个数下进行算法的分类性能比较。表1中选择4个实验数据集:Yeast、Arts、Education和Social。采用的评价指标为AP、CV、HL和RL。对比算法包括基于最大相关性的多标记维数约简(multi-label dimensionality reduction via dependence maximization, MDDM)[21],其中,MDDM算法按照参数的不同可以分为MDDMspc算法和MDDMproj算法,本节选择的对比算法为MDDMproj算法、多标记特征选择算法(multi-label feature selection ReliefF algorithm,RF-ML)[25]、基于标记权重的多标记特征选择算法(multi-label feature selection algorithm based on label weighting, LWMF)[20]、基于AP聚类和互信息的弱标记特征选择算法(weak label feature selection method based on AP clustering and mutual information,WFSAM)[24]和基于邻域粗糙集和Relief的弱标记特征选择算法(Weak label feature selection method based on neighborhood rough sets and relief, WFSNR)[1]。图1展示了4个数据集上6种算法的4个指标对比结果,其中横坐标和纵坐标分别表示所选特征个数(NF)和评价指标。
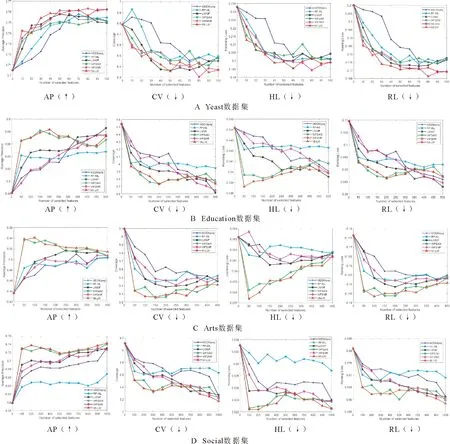
图1 6种算法在4个多标记数据集上的4个指标对比结果
对图1A分析可知,在Yeast数据集上,AP指标下,当NF=20时,MI-LW算法略低于LWMF算法和WFSNR算法,与WFSAM算法基本持平,但仍优于MDDMproj和RF-ML这2种算法。当NF=10、30、40时,MI-LW算法的AP值均优于其他算法。CV指标下,当NF=50时,MI-LW算法的CV值最优。在其他NF值上,MI-LW算法优于绝大多数对比算法。当NF> 50时,MI-LW算法的CV值虽略有上升但仍优于MDDMproj、RF-ML和WFSAM这3种算法。在HL指标下,当NF=60时,MI-LW算法的HL值最优。在其他NF值上,MI-LW算法优于绝大多数对比算法。当NF> 60时,MI-LW算法的HL值虽略有上升但优于MDDMproj、RF-ML、LWMF和WFSAM这4种算法。RL指标下,MI-LW算法在所有NF值上均优于MDDMproj、RF-ML、LWMF和WFSAM这4种算法,并且在绝大多数NF值上,MI-LW算法的RL值优于WFSNR算法。对图1B分析可知,在Education数据集上,AP指标下,当NF=200时,MI-LW算法的AP值取得最优,高于其他5种对比算法。当NF< 300时,MI-LW算法的AP值与WFSAM算法基本持平,但远远高于MDDMproj、RF-ML、LWMF和WFSNR这4种算法。CV指标下,当NF=200时,MI-LW算法的CV值取得最优,与WFSAM算法基本持平,但远远低于MDDMproj、RF-ML、LWMF和WFSNR这4种算法。随着NF取值的增大,MI-LW算法的CV值虽略有上升,但仍优于MDDMproj、RF-ML和WFSAM这3种算法。HL指标下,当NF=50时,MI-LW算法的HL值取得最优,远低于其他对比算法。当NF< 300时,MI-LW算法的HL值均优于其他对比算法。RL指标下,当NF=200时,MI-LW算法的RL值取得最优,低于其他对比算法。当NF< 300时,MI-LW算法的RL值与WFSAM算法相差无几,但优于MDDMproj、RF-ML、LWMF和WFSNR这4种算法。综合来看,当NF值较小时,MI-LW算法的分类效果优于其他5种对比算法。虽然随着NF值的增大MI-LW算法的分类性能有所下降,但因为特征选择所选的特征要尽量的少,故MI-LW算法的分类性能仍优于其他算法。对图1C分析可知,在Arts数据集上,AP指标下,当NF=100时,MI-LW算法的AP值取得最优,远高于其他5种对比算法。当NF取其他值时,MI-LW算法的AP值虽略有下降,但在绝大多数NF值上仍优于其他5种对比算法。CV指标下,当NF=150时,MI-LW算法的CV值取得最优。当NF取其他值时,MI-LW算法的CV值远远优于MDDMproj、RF-ML、LWMF和WFSNR这4种算法。HL指标下,当NF=50时,MI-LW算法的HL值远远优于其他5种对比算法。当NF> 50时,MI-LW算法的HL值虽有所上升,但仍优于MDDMproj、RF-ML、LWMF和WFSNR这4种算法,并且在绝大多数NF值上,MI-LW算法的HL值优于WFSAM算法。RL指标下,当NF=100时,MI-LW算法的RL值取得最优。当150 为了更清晰地了解6种算法在上述5个指标下的最优值的对比结果,表4列出了6种算法(MDDMproj、RF-ML、LWMF、WFSAM、WFSNR和MI-LW)在4个数据集(Yeast、Education、Arts和Social)上的关于5个指标(NF、AP、CV、HL和RL)上的分类结果。从表4中可以明显看出,在AP指标下,MI-LW算法的AP值在Education、Arts和Social这3个数据集上取得最优。在Yeast数据集上,MI-LW算法的AP值仅比最优WFSNR算法的AP值低了0.005 1,但它的NF值比WFSNR算法低了30。在CV指标下,MI-LW算法的CV值在Education数据集和Arts数据集上取得最优。在Yeast数据集上,MI-LW算法的CV值比WFSNR算法的CV值高了0.053 4,但它的NF值比WFSNR算法低了30;在Social数据集上,MI-LW算法的CV值比WFSAM算法和LWMF算法的CV值高了0.060 3和0.046 7,但它的NF值比WFSAM算法和LWMF算法低了100和500。在HL指标下,MI-LW算法的HL值在Education数据集、Arts数据集和Social数据集上取得最优。在Yeast数据集上,MI-LW算法的HL值比WFSNR算法的HL值高了0.005 1,但它的NF值比WFSNR算法低了30。在RL指标下,MI-LW算法的RL值在Education数据集、Arts数据集和Social数据集上取得最优,在Yeast数据集上,MI-LW算法的RL值比WFSNR算法的RL值高了0.004 2,但它的NF值比WFSNR算法低了30。因此,综合5个指标来看,MI-LW算法的分类性能优于其他5种对比算法。 表4 4个数据集上6种算法的5个指标的对比结果 接下来,本节使用Friedman统计检验[26]和Bonferroni-Dunn统计检验[24]来讨论所有算法对于各个评价指标的统计结果,计算公式为 (11) (12) 根据表2的实验结果,MI-LW算法和其他3种对比算法:ReliefF、ReliefF+I-Cor和I-ReliefF+Cor在5种指标上的平均排名对应的χF2和FF值如表5所示,对应的CD图如图2所示。 表5 4种算法在5个评价指标上的统计结果 由表5分析可知,在显著性水平α取值为0.1时,则qα=2.128,CD=1.468 5,其中T=7,s=4。从图2中可以明显看出MI-LW算法在AP、CV、RL和OE这4个指标下都优于其他3种对比算法。在AP和CV这2个指标下,MI-LW算法明显优于ReliefF算法和I-ReliefF+Cor算法,且MI-LW算法与ReliefF算法具有显著差异;在HL指标下,MI-LW算法明显优于ReliefF和I-ReliefF+Cor这2种算法,且MI-LW算法与ReliefF算法具有显著差异;在RL指标下,MI-LW算法明显优于ReliefF算法和ReliefF+I-Cor算法,且MI-LW算法与ReliefF算法具有显著差异;在OE指标下,MI-LW算法明显优于ReliefF算法和I-ReliefF+Cor算法,且MI-LW算法与其他3种算法具有显著差异。 图2 ML-KNN分类器下4种算法的Bonferroni-Dunn测试结果 根据表3的实验结果,MI-LW算法和其他7种对比算法:MDDMspc算法、MDDMproj算法、PMU算法、MLNB算法、MUCO算法、WFSNR算法及WFSAM算法在4种指标上的平均排名对应的χF2和FF值如表6所示,对应的CD图如图3所示。 表6 8种算法在4个评价指标上的统计结果 由表6分析可知,在显著性水平α取值为0.1时,则qα=2.450,CD=4.243 5,其中T=4,s=8。从图3中可以明显看出MI-LW算法在4个指标下都优于其他7种对比算法。在AP指标和CV指标下,MI-LW算法的性能明显优于MDDMproj算法、WFSNR算法、PMU算法和WFSAM算法;在RL指标和OE指标下,MI-LW算法的性能明显优于WFSNR算法、MLNB算法、MDDMproj算法和WFSAM算法;在AP、RL、OE和CV这4个指标下,MI-LW算法与其余7种对比算法具有显著差异。 图3 ML-KNN分类器下8种算法的Bonferroni-Dunn测试结果 根据表4的实验结果,MI-LW算法和其他5种对比算法:MDDMproj算法、RF-ML算法、LWMF算法、WFSAM算法及WFSNR算法在4种指标上的平均排名对应的χF2和FF值如表7所示,对应的CD图如图4所示。由表7分析可知,在显著性水平α取值为0.1时,则qα=2.326,CD=3.077 0,其中T=4,s=6。从图4可以看出,MI-LW算法在4个指标上优于其他5种对比算法。在AP、CV、HL和RL这4个指标下,MI-LW的性能明显优于RF-ML、MDDMproj与WFSNR这3种算法;在AP指标下,MI-LW算法与其他5种算法具有显著差异;在CV、HL和RL这3个指标下,MI-LW算法与MDDMproj和RF-ML这2种算法具有显著差异。 表7 6种算法在4个评价指标上的统计结果 图4 ML-KNN分类器下6种算法的Bonferroni-Dunn测试结果 目前,一些多标记特征选择算法未充分考虑特征和标记之间的相关性,并且传统ReliefF算法中样本之间分类间隔较大导致出现分类无意义,以及算法分类精度偏低的问题,为了解决上述缺陷,设计了一种基于标记相关性和改进ReliefF的多标记特征选择方法。首先,为了有效反映特征与标记集的相关性并提高算法的分类精度,使用正类样本在标记集合中的所占比例给出标记权重定义,通过结合互信息和标记权重提出了特征与标记集合之间的相关度。然后,为了解决传统ReliefF算法中因样本间距离过大导致异类样本和同类样本失效的不足,引入传统ReliefF算法中的距离分别计算样本与最近邻异类样本、最近邻同类样本的距离,基于异类样本和同类样本数量提出了新的样本分类间隔,结合标记权重与分类间隔给出了一种新的特征权值更新公式。最后,结合标记相关性和改进的ReliefF算法,构建了一种新的多标记特征选择算法。在7个多标记数据集上使用6个评价指标与相关多标记特征选择算法进行对比分析,仿真实验结果表明了所提算法是有效的。但是,当数据集的标记集为稀疏矩阵时,所提算法无法很好地处理此类数据集。因此,在以后的研究工作中,针对缺失标记数据集,结合粗糙集、聚类等理论,研究弱监督特征选择方法。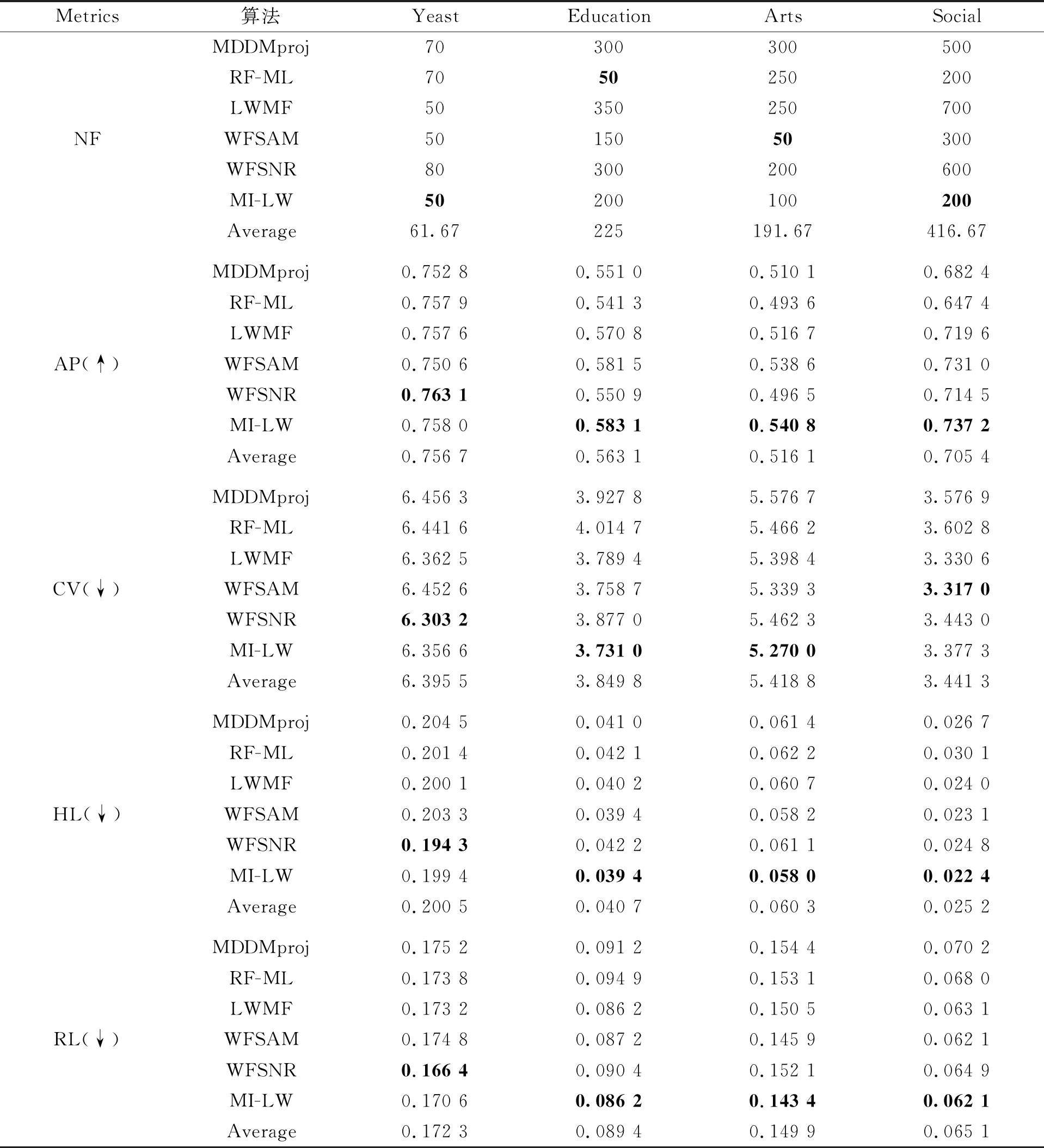
3.3 统计分析







4 结语

