电场与声场作用下微细通道内R141b 压降特性

罗小平, 许静姝, 杨书斌, 李景生, 张超勇

(华南理工大学 机械与汽车工程学院, 广东 广州 510640)

1 前 言

近年来微细通道换热器被广泛应用于医疗设备、核工业、家用电器等领域[1-3]。通常来说，提高换热效率的解决办法是将微细通道内部设计成特殊结构，但这种方法加工成本大，操作弹性差，因此最理想的解决办法是引入电场、电磁场、声场、超重力等物理场[4-7]。其中外加声场和电场作为主动强化传热技术，近年来已被相继应用于各领域[8]。超声波场具有能量密度高、穿透性好的优点，能够强化微细通道中弹状流的气液传质，提高传热系数[9]。而电场作为一种常见外场，优点是易获得、成本低，能够增强微细通道内液体的不稳定性和压降，增强液滴破碎速度，从而形成更小的液滴[10]。因此可将超声波和电场引入微细通道换热器中以改善其综合性能。

目前，一些学者就超声波对沸腾传热压降的影响进行了研究[11-12]。段希利等[13]研究了在不同超声波功率下不同换热管的传热和流动性能，得出结论：超声振动可以明显提高换热器的传热系数，最大传热系数可提高3 倍，并且可增加换热管内的流体压降，主要原因是超声振动的空化作用致使层流边界层被破坏。Delouei 等[14-15]研究了纳米颗粒和超声波振动对流体传热和压降的同时影响，结果表明，超声场的存在可以增强纳米流体的传热，最高可达15.27%；此外增加雷诺数会减少超声波振动对压降的影响。还有一些学者就电场对沸腾传热压降的影响进行了研究。刘丰良[16]研究了电场和脉动流同时作用下对换热器的强化影响，结果显示当电场和脉动流同时作用时，传热系数相较于单独场作用时会进一步得到提高，最大可达1.25 倍，同时压降也随着脉冲频率增大而增大。Yin 等[17]研究了基于交流电场作用下的流动微细通道中液滴动力学，当电场的频率增加，流体的液滴生长速率也会增加，从而增大了压差。

以上学者更多关注单一外场对于常规尺度沸腾强化规律的作用，而对于两场协同且在微细尺度方面研究较少。目前He 等[18]重点探讨了在超声场和电场同时作用时的微细通道传热特性，而压降特性也是衡量设备传热的重要参考性能之一，因此本研究将采用复合强化传热技术，研究两场同时作用对微细通道压降以及强化传热综合性能的影响。

2 实验系统与数据处理

2.1 实验系统

如图1 所示为实验系统，实验系统主要由实验段装置、加热装置、冷却装置、液体循环驱动装置、实验数据采集装置、限流调压装置组成。在实验系统中，工质R141b 循环流动动力由磁力泵提供，经预热水箱预热后，工质以液态流入实验段，同时，加热板将工质加热沸腾至气液两相状态并从出口流出，随后进入冷却水箱冷却至液相状态回到磁力泵，形成稳定循环闭合回路。其余主要部件功能为：数据采集系统用于数据采集，调节阀等用于调节工质流速，压力表与测温仪用于监测磁力泵与实验段两端的压力和温度变化，声场发生器用于施加声场环境，高压直流电场发生器用于施加电场环境。

图1 实验系统Fig.1 Schematic diagram of the experimental system

2.2 系统实验段

为保证电场与超声场能够同时作用于微细通道内，本研究设计了如图2 所示实验段，从上至下依次为紧固螺栓、聚四氟乙烯盖板、密封垫圈、可视化玻璃、线状电极组件、超声波布置装置、微细通道热沉、基座、加热板。在基座的一侧开有8 个测压孔，包括进出口测压孔、通道内沿程测压孔，测压采用HC3160-HVG4 型压力传感器。在盖板与玻璃、盖板与基座之间使用O 型橡胶圈进行密封，拧紧盖板上的26 个螺栓压紧密封圈保证实验段密封性良好。在基座底部对应微细通道位置放置一块云母加热板，并在之间涂有一层导热硅脂，保证加热功率稳定传输。

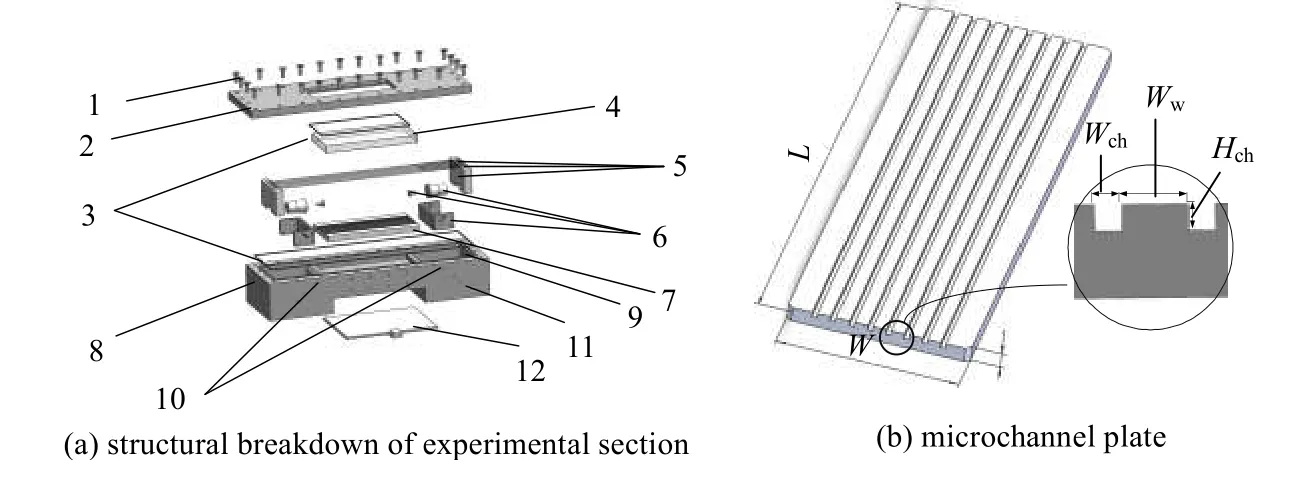
图2 系统实验段Fig.2 Schematic diagram of the experimental device structure

本次微细通道热沉如图2(b)使用的是6061 铝合金，总共有11 条平行槽道，微细通道板总长度L为220 mm，微细通道板总宽度W为100 mm，单条通道的宽度Wch为2 mm，高度Hch为2 mm，微细通道板肋宽度Ww为4 mm。

2.3 实验步骤

实验前应采用R141b 工质对实验系统进行循环清洗，其中实验段部分应采用超声波清洗机对其进行震荡清洗。清洗完毕后用氮气对整个系统进行气密性检查，最后为防止实验系统内残留气体干扰实验过程，应在实验前将实验系统抽至真空状态，当真空表压力数为-101 kPa 时，关闭真空表，方可进行实验。

实验具体操作：将R141b 注入储罐中，通过磁力泵驱动，调节变频器频率控制泵的转速，通过调压器输出电压控制加热板的输出功率，通过调节阀调节进出口压力、温度，实验电场所需的电压由高压直流电场发生器进行控制，实验声场所需的能量由超声波发生器发出，并由超声波换能器转换。

2.4 实验数据处理

2.4.1 质量流量

式中：qm为质量流量，kg·s-1；ρ为工质R141b 初始密度，kg·m-3；qV为流量计测得的体积流量，m3·s-1；qm,G为单个微细通道单位面积的质量流量，kg·s-1；N为微细通道的数量；d为通道直径，m。

2.4.2 热流密度

式中：q为热流密度，W·m-2；P为加热板功率，W；S为加热板面积，m2；

系统在实际运行过程中，不可避免有部分能量以自然对流传输到空气中，因此，有必要估算出微细通道内的有效热流密度：

式中：qeff为有效热流密度，W·m-2；ε为热损失效率。

目前有学者[19-21]采用单相热平衡实验来估算实验段的热损失，热损失率计算式如下：

式中：Φ为热流量，W；cp,i为对应压力下R141b 比定压热容，J·kg-1·K-1；tin、tout分别为进口和出口工质温度，℃；

气液两相段压降包括Δptp,g、Δptp,a和Δptp,f，计算公式分别如下[22]：

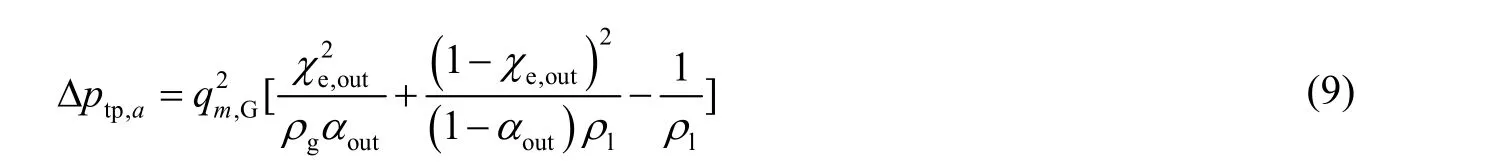
式中：g为重力加速度，m·s-2；Ltp为汽液两相段长度，m；Δptp、Δptp,g、Δptp,a、Δptp,f分别为气液两相段压降、两相重力段压降、两相加速压降、两相摩擦压降，Pa；ρg、ρl分别为工质气相密度、工质液相密度，kg·m-3；χe,out为出口的热力平衡干度；αout为出口空泡率；

2.4.3 误差分析

实验数据的误差主要来自仪器测量与数据处理误差，其中仪器测量误差为直接测量误差，数据处理误差为计算参数误差。在本实验中直接测量误差包括流量数据误差、温度数据误差、压力数据误差。

直接测量误差：

本实验使用的仪器均有一定的精度如表1 所示为直接测量误差，为尽可能缩小测量带来的误差，实验采用精度为2.5%的DK-800-6(F)转子流量计，精度为0.2% 的QDW90A 压力传感器。

表1 直接测量误差Table 1 Error results of direct measurements

计算参数误差：

间接物理量Y是直接测量值X1，X2，…，Xn的相关函数，Y=f(X1，X2，…，Xn)，由于X1，X2，…，Xn在测量的过程中存在不确定度δ1，δ2，…，δn，因此对Y的误差计算如下[23-24]：

则Y的相对不确定度为

本实验所用微细通道加工精度为0.01 mm，测量精度为0.02 mm，功率表精度为0.5%，根据式(10)与(11)，可以得出间接物理量的相对不确定度，见表2，其中Lsp为单相段的长度，m。

表2 相关物理量不确定度Table 2 Uncertainties of related physical quantities

3 实验结果分析

3.1 有无物理场作用下微细通道两相压降分析

3.1.1 单一物理场对两相压降的影响

图3(a)是在实验电压为0～800 V、进口温度tin=34 ℃、qm,G=115.91 kg·s-1的微细通道内R141b 的电场作用下，两相压降随热流密度的变化情况。从图3(a)中可以看出，系统的两相压降随着热流密度的增大而增大，如热流密度在9.66 kW·m-2时，电压为0 V 时的两相压降为1 087.4 Pa，电压为400、600、800 V时的两相压降分别为1 156.24、1 221.28、1 286.6 Pa，相对无电场时分别提高了6.33%、12.31%、18.32%。这是由于随着热流密度的增大，过冷沸腾起始点向通道上游移动，通道换热壁面上核化点增多，气泡量也明显增多，使得通道内两相区的长度明显增大，两相压降随之增大。

图3 单一场作用下两相压降随热流密度变化情况Fig.3 Variation of two-phase pressure drop as a function of heat flux under single fields

图 3(b)是进口温度tin=34 ℃、qm,G=115.91 kg·s-1，施加超声波23 kHz+50W、40 kHz+50 W、23 kHz+12.5 W、40 kHz+12.5 W 以及无声场作用下的R141b 工质的两相压降随热流密度的变化情况。观察图3(b)两相压降的变化趋势，发现当功率一定时，频率越小，两相压降越大，如在热流密度为9.66 kW·m-2，功率为50 W 时，频率由40 kHz 下降到23 kHz，两相压降分别为1 247、1 311.8 Pa，增大了5.19%，由此可见低频超声对两相压降的影响更大。同时，当频率一定时，增大功率也会使得两相压降增大，如频率为23 kHz时，当功率由12.5 W 增大到50 W，两相压降增大了10.28%，这是由于超声波频率的减小或功率的增大均会诱导小气泡产生，使气泡运动变得复杂，两相压降增大。为了便于比较下文将功率固定为50 W。

3.1.2 电场与声场同时作用对两相压降的影响

图4 为电场与声场作用下两相压降随热流密度的变化情况，图中c1～c9 为工况(见表3)，从图4 中可看到，在电场与声场同时作用下的两相压降变化与单独外场作用下的趋势一致，如热流密度在9.66 kW·m-2两相压降相较工况1 无物理场作用时分别增大了6.33%、18.32%、20.64%、25.58%、30.59%、10.99%、15.54%、20.14%。可以看出两场同时作用下的两相压降明显大于单一物理场作用下的两相压降，增加量最大的为工况6，同时施加800 V 电压和23 kHz 超声场。原因是电场与声场协同后通道内的蒸气量明显增大，两相区长度大于单一物理场作用下的长度，从而两相压降明显增大。

表3 电场与声场作用下两相压降的工况Table 3 Working conditions of two-phase pressure drop under electric and ultrasonic fields

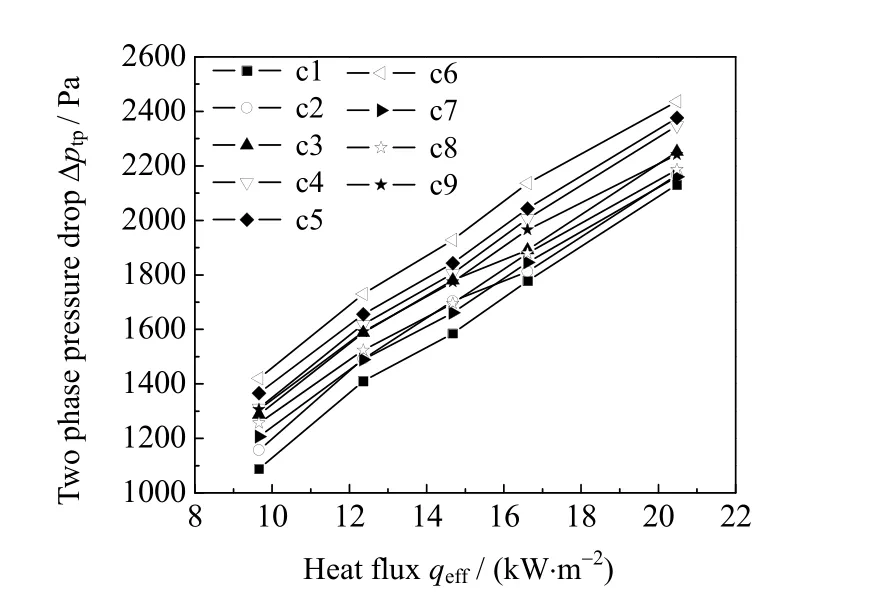
图4 电场与声场作用下两相压降随热流密度变化情况Fig.4 Variation of two-phase pressure drop as a function of heat flux under electric and ultrasonic fields

3.2 微细通道不稳定性功率谱密度及可视化研究

3.1 节对不同工况下的两相压降进行分析。但微细通道内流动沸腾不稳定是一种复杂的非线性行为，为了进一步认识这一现象，本研究将对两相压降的频域进行分析，以得到信号能量在频域中的分布[25]。这里引入功率谱密度 (power spectral density，PSD)[26]来分析流动沸腾过程中的压降波动信号，它揭示了时域信号能量的频域分布和能量密度，信号的峰值即为信号的主频率。

在进行PSD 分析前，需将两相压降波动信号中的直流成分去除，这里采用MATLAB 通过对原始信号与其平均值做差的方法去除[27]。图5 为电场与声场作用下的两相压降的功率谱密度分析曲线、图6 为对应情况的可视化分析，工况：qm为115.91 kg·s-1、q为14.68 kW·m-2、采样频率为5 Hz、稳态采集数据点为100 个。为了便于比较，超声波的施加条件统一为频率23 kHz、功率50 W。整体可以看出曲线趋势呈现单峰特征。图5(a)、(b)、(c)分别为无外场、施加400、800 V 电场时的两相压降的PSD 随频率变化的特征，其峰值所对应的频率分别为0.90、1.24、1.34 Hz；最大幅值分别为0.59、0.47、0.40 kPa2·Hz-1。两相压降主频频率则随着电压增大而增大，而主频PSD 的幅值随着电压增大而减小。结合图6(a)、(b)、(c)可视化分析可以看出，这是由于当微细通道内施加电场时，气泡生长速率加快，震荡周期缩短，以至频率增大。而施加电场后，气泡整体呈泡状流，形成的受限气泡长径比减小，气泡生长受限减弱，因此主频幅值减小。

鲁迅曾对许广平说他思想的矛盾在于“人道主义”和“个人主义”的消长起伏，所以他“忽而爱人，忽而憎人”[7]493。这是诗人对于自己爱憎悖论的解释，他通常都是在爱憎不相离的意义上强调它们的关系和价值。

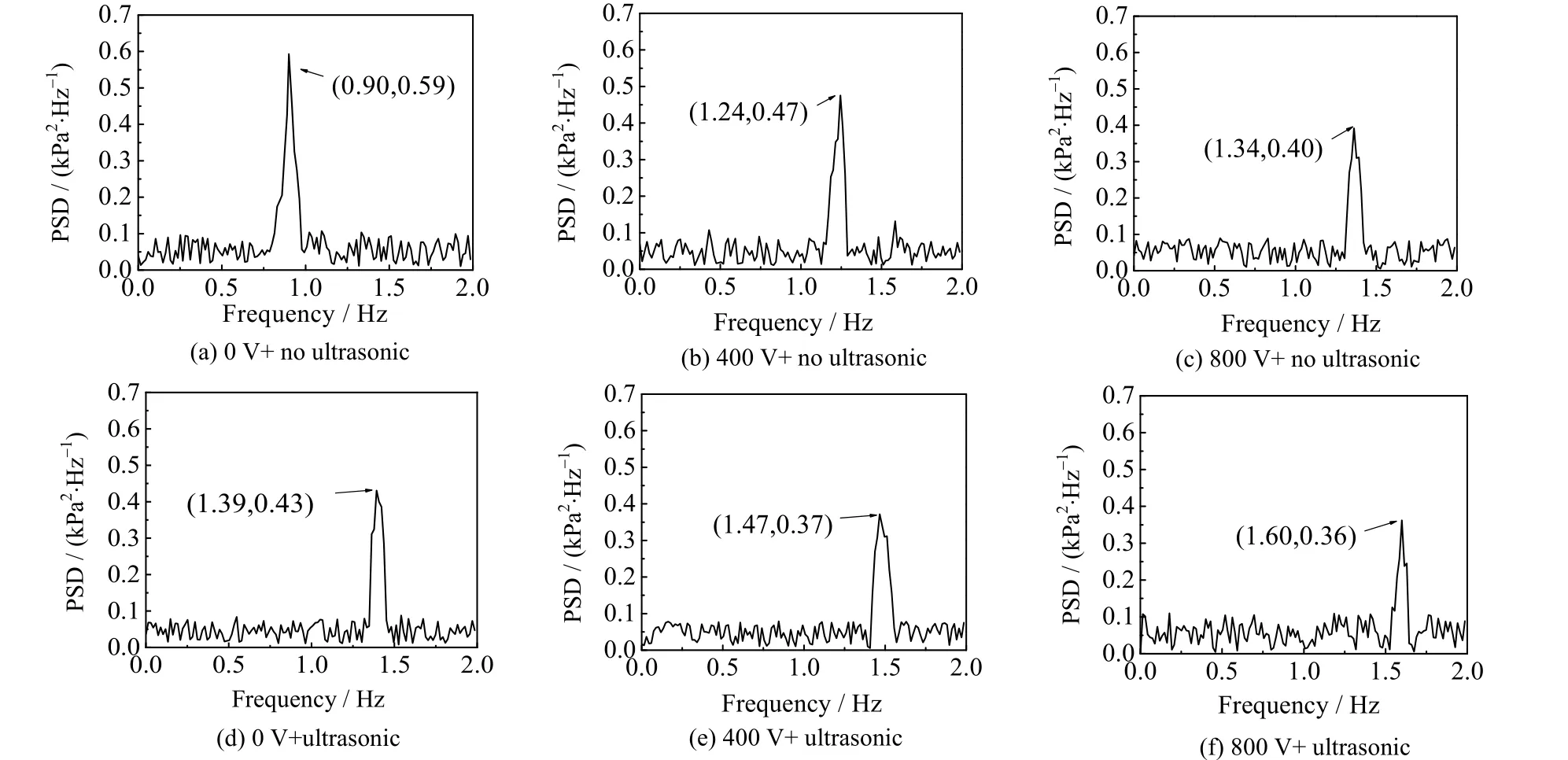
图5 电场与声场作用下的两相压降频域波动特性Fig.5 Power spectra of two-phase pressure drop under electric and ultrasonic fields

图6 电场与声场作用下的可视化Fig.6 Visualization results under electric and ultrasonic fields

对比图5(a)、(d)发现当单独施加超声波时，主频频率增大至1.39 Hz，PSD 幅值减至0.43 kPa2·Hz-1。结合图6(a)、(d)可视化分析可以看出，这是由于超声波声流作用加速了气泡脱离，减少气泡震荡周期，气泡变小，数量增多，气泡呈高频低能状态，图中Z为气泡长度。观察图5(a)、(e)、(f)，发现在400、800 V 电场与声场的同时作用下，频率分别增大为1.47 和1.60 Hz，PSD 幅值分别减小为0.37、0.36 kPa2·Hz-1。相对单一场作用时，两场同时作用下的频率进一步增大，PSD 幅值进一步减小。根据图6(a)、(e)、(f)可知，这主要是两场同时作用时进一步加剧了通道内气泡流动速度，气泡更加密集，通道内气象成分增多。

3.3 电场与声场同时作用下对微细通道的强化传热综合性能评价

经3.1 节和3.2 节分析可知，不论电场还是声场均能对微细通道压降产生影响，但压降仅仅是衡量强化技术有效性的一种指标，如果能结合当前工况下的传热性能统一评估2 种外加强化技术，则能更好证明其应用价值，因此本研究引入Webb-Bergles 方法[28]，定义强化传热综合性能评价(performance evaluation criteria，PEC)。

式中：hi、he分别为未施加物理场和施加物理场时沸腾强化传热系数，W·m-2·K-1；Δi、Δ分别为未施加物理场和施加物理场时单位长度两相压降，Pa；

该方法的主要思想是综合考虑未施加物理场与施加物理场时的沸腾强化传热系数和单位长度两相压降，并以未施加物理场时的两项参数为基准，简单直观地反映所施加强化传热技术的优劣。当PEC＞1 时，说明该种物理场施加方式能够有效提高微细通道热沉的综合性能，否则，说明该物理场施加方式所带来的换热性能提升较小。

本实验中外加电场电压最大为800 V，电流为0.5 μA，电场功率为0.000 4 W。外加声场的最大功率为50 W，但实际微细通道两相流消耗的超声波功率较小，仅为0.45 W，与最小电加热功率176 W 相比，电场与声场功耗较少，均可忽略不计。在声场的热效应方面，采取控制变量法仅对工质进行超声波换能，不额外加热时，结果显示工质温度仅上升0.03 ℃，可以忽略因施加超声波带来的热效应。

图7 为表3 所示工况下的沸腾强化传热系数。从图中可以看出，相对于无外场作用下，施加外场时沸腾传热系数均有明显提升，由原来的2.3 至2.6 W·m-2·K-1上升到2.8 至4.7 W·m-2·K-1不等。根据式(12)计算得到如图8 所示的PEC 随热流密度变化的影响。从图8 中可以看出，除工况1 无外场作用下的传热综合性能评价因子为1 外，其他所有工况作用下的PEC 均大于1，即施加外场均可有效提升微细通道的综合换热性能。且综合换热性能均在一定程度上受到热流密度的影响，具体表现为随着热流密度的增加而减小。这是由于低热流密度时，通道内以泡状流为主，在此流形基础上，传热强化量大于流阻的增大量。而随着热流密度的增加，传热效果虽然增强，但流阻也进一步增大，因此传热综合性能逐渐降低。此外，在同一热流密度下，电压越高、超声波频率越低，综合性能越高。如热流密度在9.66 kW·m-2时，800 V 电场与23 kHz 和40 kHz 超声波同时作用下的PEC 指数分别为1.78、1.75，400 V 电场与23 kHz和40 kHz 超声波同时作用下的PEC 指数分别为1.64、1.60。

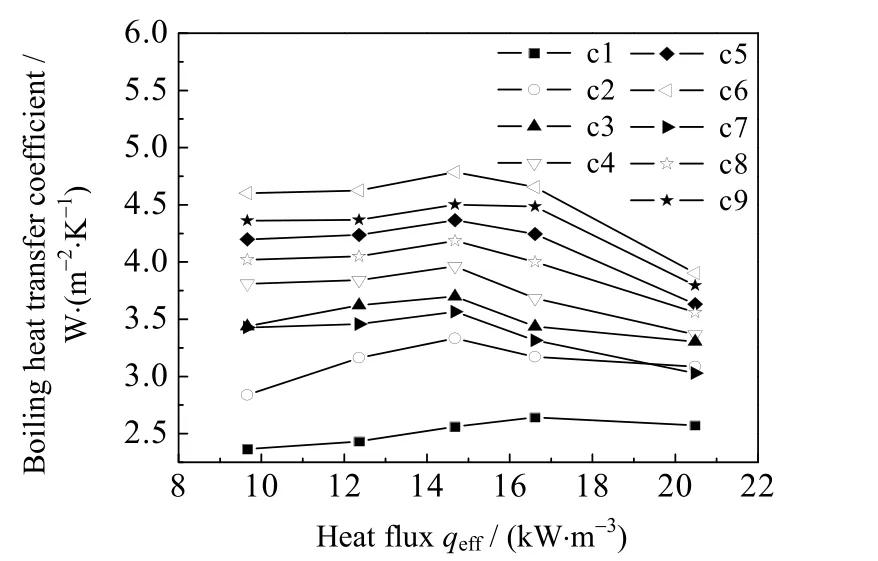
图7 不同工况下沸腾传热系数的变化趋势Fig.7 Profiles of boiling heat transfer coefficient under different working conditions

图8 不同工况下PEC 的变化趋势Fig.8 Profiles of PEC under different working conditions

4 结 论

本研究对单独电场、声场及其同时作用下的微细通道压降特性进行了研究，并对微细通道内两相流压降的不稳定性、综合热性能进行了分析，主要结论如下：

(1) 在电场或声场的单独作用下，微细通道内两相压降随热流密度的增大而增大。在单独电场作用时，电压为400～800 V 的工况下，两相压降随电场电压升高而升高。在单独声场作用下，功率为50 W 不变时，频率由40 kHz 下降到23 kHz，两相压降增加5.19%；当频率为23 kHz 不变时，功率由12.5 W 增加到50 W，两相压降增大了10.28%，说明在本实验范围内超声波频率越小、功率越大、两相压降越大。

(2) 在电场与声场同时作用下，两相压降明显大于同一工况下单独电场或声场作用下的两相压降。在热流密度为9.66 kW·m-2时，施加800 V 电压和超声波频率23 kHz、功率50 W 时，两相压降变化最大，增加了30.59%。

(3) 根据功率谱密度及可视化分析，分别施加电场、声场时，功率谱密度主频增大，主频幅值减小。当电场与声场同时作用时，功率谱密度主频进一步增加，通道内气泡运动加剧，气泡更加密集，主频频率最高升至1.60 Hz，对应幅值为0.36 kPa2·Hz-1，这说明电场与声场同时作用时，微细通道内主流受限气泡的运动周期缩短、气泡长径比减小、运动速度增加。

(4) 通过对比有无电场及声场作用下的微细通道强化传热综合性能，在本实验工况下，电场与声场同时作用时的传热综合性能最佳，PEC 因子最高可达1.78。而单独外场作用下的PEC 为1.15～1.51。与高热流密度工况相比，低热流密度可以获得更高的强化传热综合性能。