基于粒子群优化算法的分立系统的分形模型
兰歆
(山东工程职业技术大学 山东省济南市 250200)
1 引言
随着现代科学技术的飞速发展,对各种工业的要求和精度要求越来越高。在航空导航机器人制造业的迫切解决方案倒立摆系统由机器人技术,计算机控制理论和控制系统。它具有结构简单、物理参数和形状变化小等优点。可作为典型控制对象来研究是否控制理论或方法是可用的[1-3]。
近年来,控制工程的控制系统越来越复杂。传统控制理论和现代控制理论都是基于模型的控制研究。目前,在零初始条件下建立的倒立摆的传递函数,即其整数阶数数学模型较多。然而,数学模型是远离真实的模型,不适合在工程对象控制系统的研究。本文采用人工智能算法的参数辨识方法,建立了一个分形数学模型。因此,这项研究具有深远的理论价值和广阔的应用前景。
系统辨识是利用系统运行或试验过程中测得的系统输入输出数据建立系统数学模型的技术科学,系统数学模型是指系统本质特征的数学抽象。内部和外部因素之间的关系反映在系统内部和外部因素。建立了系统的数学模型和预测系统的未来[7-8]。
本文利用群体智能算法,利用参数识别的思路,建立了倒立摆分立模型,并通过Matlab/Simulink软件将该分数阶数学模型与自己的系统模型进行比较。PID控制是一个广泛应用的控制系统,但三自由度是不足以解决所有的问题。
2 学习免疫合成的粒子群优化算法
人工免疫系统[9-11]是模仿生物免疫进化过程的人工智能系统。免疫机制的主要特点包括克隆,基因突变,抗体结合,抗原和免疫记忆的形成等。免疫调节机制允许受体细胞在特定条件下改变结构。抗体循环补充算子每天有大量新抗体进入免疫系统,确保抗体群的多样性。
人工免疫系统的基本定义[4-6]
在进化算法中,抗原一般指的是免疫系统中的逆函数和逆函数。该问题的目标函数是人工免疫算法和重要的测量标准的初始阶段。
在进化算法和抗体序列中,抗体是类似于个体免疫系统的典型候选抗体。实际上,常见抗体以编码形式出现,常见编码形式有二进制和十进制。
抗体-抗原的亲和性:为了反映抗体的单一结合位点与一价抗原(或表位)的结合性,抗体的抗原对原亲和性的大小通常用亲和性来表示。在免疫系统中,这一概念是用来显示抗体在不同位置的原始或客观的功能。
抗原和抗体之间的关系反映了抗体和抗体之间的结合能力。在人工免疫系统中,一般指候选解之间的距离,二进制编码一般采用解释距离,实数编码一般采用范数,大部分是欧几里德距离。
记忆单元:在人工免疫系统中,记忆单元是由特定抗体组成的抗体群,用于维持种群多样性和求解过程中的最优解。
克隆:生物增殖过程。免疫算子是一种基于选择定理的复杂算子。
介绍了CLPSO算法中免疫系统的机制,建立了一种新的免疫系统CLPSO模型。AIS-CLPSO算法一方面汲取CLPSO多样性机制另外一方面,融合了人工免疫系统(AIS)收敛速度快、求解精度高的优点AIS-CLPSO计算模型构建于四个部分:
(1)综合学习粒子群算法(CLPSO);
(2)免疫克隆选择操作;
(3)被摄体编辑;
(4)补充抗体循环。
AIS- CLPSO计算图如图1所示。
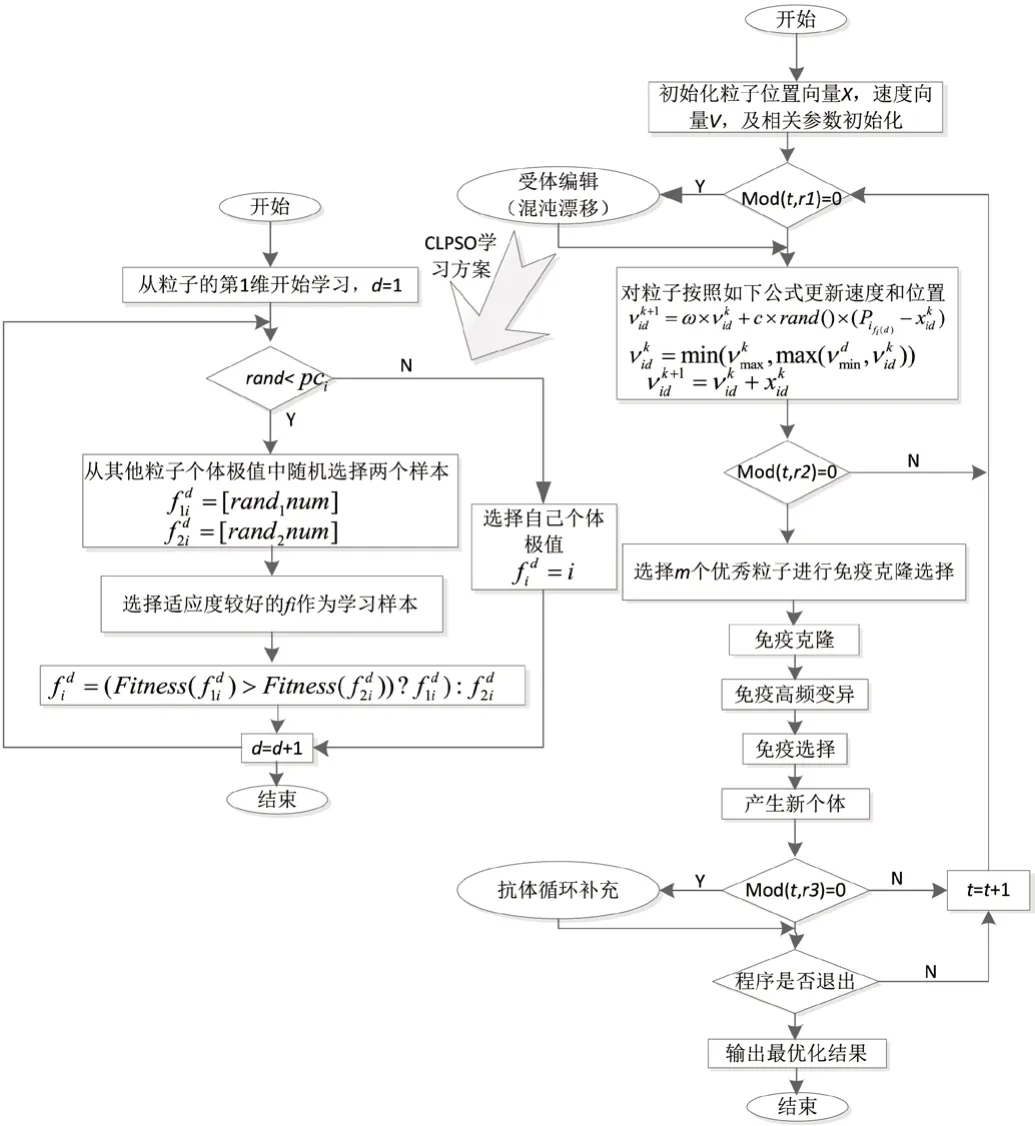
图1:AIS-CLPSO算法辨识参数流程图
2.1 免疫克隆选择操作
在CLPSO算法中,个体最大运动不能进行有效的局部搜索。为了提高个人免疫系统的全局优化,CLPSO使用的大部分机制。要执行以下操作,请执行以下操作:
(1)选择适应度高的m个个体极值,每个粒子的个体极值构成临时种群Temp{A1d,A2d,…,And},将临时种群视为免疫系统中的抗体,克隆规模与亲和力成正比,克隆倍数Nc如下:
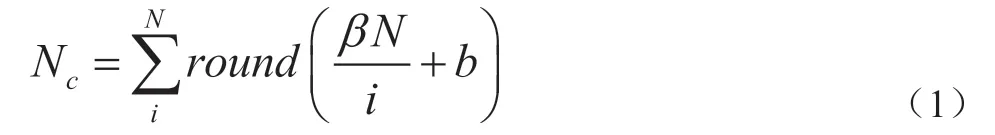
在公式中,N是群集大小。β∊(0,1),常量b≥1的整数,确保所有抗体都有一定的克隆数量。经过克隆扩增生成新组Sub。
(2)在子组的高免疫频率的变化,采用多方向的变化策略在邻近地区的水平。其变异算子如下:

在表达式中,rand()为随机数;Pm=0.5。

在式中,t是群体当前的进化代数。T是整体进化代数。b为正常数,一般取2。由式(2.13)可知,在进化初期,对于小r值ƞ(t)≈1,此时变异空间大然后在进化后期,当t接近T时ƞ(t)≈0,在小范围空间内进行局部搜索。
(3)在下一代的克隆和变异的最佳关系的人的选择
2.2 受体编辑
群体中的一些个体可能失去活性而陷入局部点,需要随机、规则的大漂移机制使失去活性的个体摆脱局部极值点。参考免疫系统中的受体编辑机制,移动陷入局部点的个体。在AIS-CLPSO算法中,每隔一定的代数鉴定惰性的细胞受体,具体参照文献,对其中20%左右的个体进行受体编辑操作。对于惰性细胞受体,使用遍历性良好的非线性Logistic序列进行随机、规则的位置大漂移。
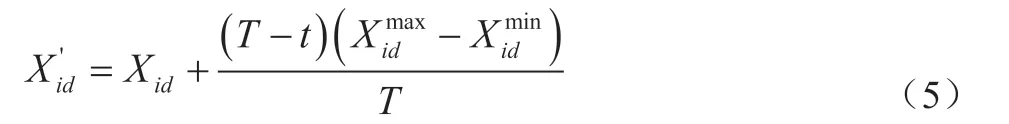
2.3 抗体循环补充算子
对适应度值不高、年龄老化的颗粒采用抗体循环补充算子进行更新,可通过抗体循环补充运算算法对注入群体的新生血液增强抗体多样性。
3 仿真结果与分析
本文采用深圳高公司直线倒立摆模型,在Matlab软件平台上进行仿真和调试。为了减少实验统计误差,实时控制系统控制执行50次,最大迭代次数为100次,避免了粒子数对算法的影响,所有粒子群算法中粒子规模为100。
惯性权重设置会影响粒子全局和局部搜索能力之间的平衡。其中较大的惯性值将增强全局搜索能力。加速因子可以调整自己的经验和群体经验,影响粒子运动轨迹。
本文利用4种惯性权值求解的基准函数进行了模拟仿真实验,采用参数调整方法提高了算法的性能和收敛速度。ω∈[0.9,0.4],在c1=c2=1.49445范围内,AIS-CLPSO算法的迭代效果良好。
运行结果:

图2和图3仿真结果表明,在识别AIS-CLPSO算法参数优良时,具有快速收敛性。另外,避免了PSO算法容易陷入局部最优的情况,弥补了APSO算法在多模式问题上的缺陷,避免了CLPSO算法存在两个缺陷。
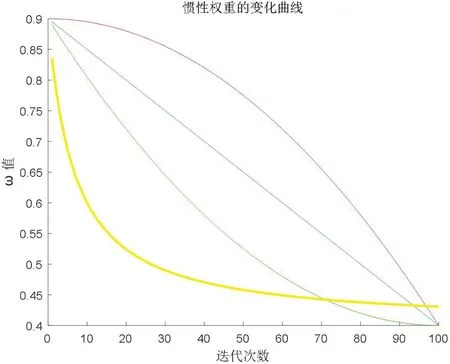
图2:4种惯性权重ω的变化曲线
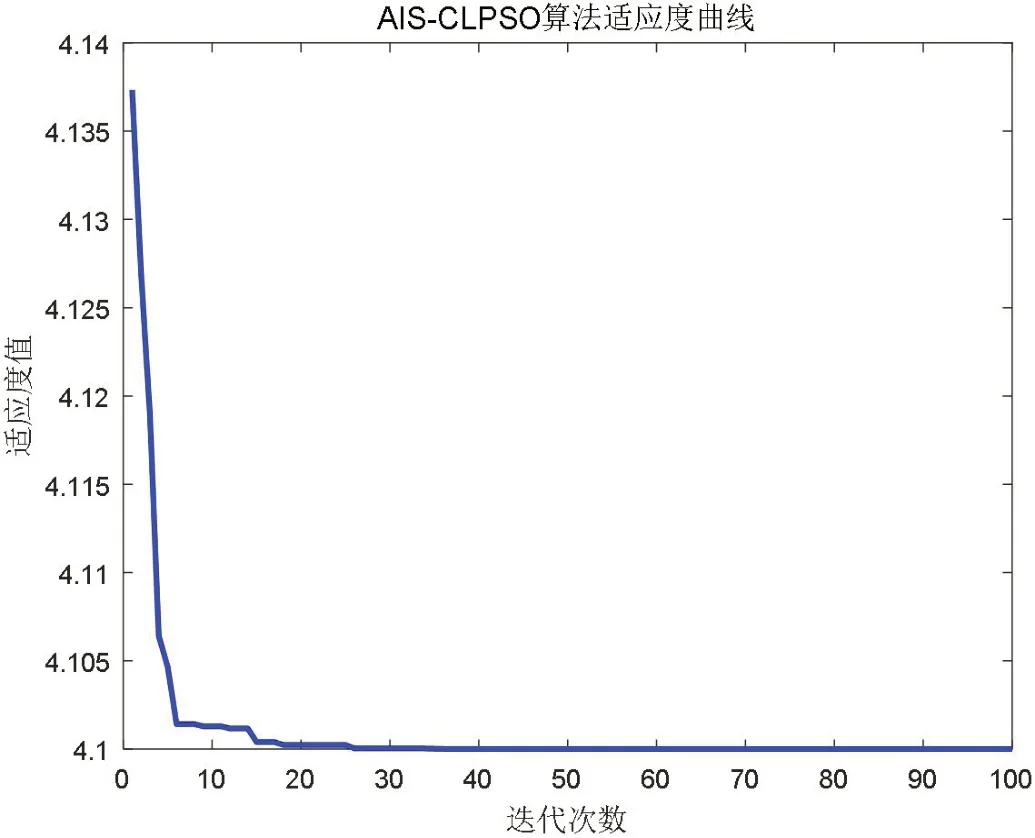
图3:AIS-CLPSO算法适应度函数曲线
(1)随机从两个粒子中选择较好的Pbest粒子,当前粒子学习样本,学习的粒子不一定能获得最好的信息。
(2)当Pbest最大值组落入局部优化,不保证有效的逃逸机制。局部极值影响整体群优化。
4 仿真验证与分析
本文采用深圳高公司直线倒立摆模型,在Matlab软件平台上进行仿真和调试。为了减少实验统计误差,实时控制系统控制执行50次,最大迭代次数为100次,避免了粒子数对算法的影响,所有粒子群算法中粒子规模为100。
PSO算法中ω∈[0.9,0.4], c1=c2=1.49445;APSO 算法中ω∈[0.9, 0.4], c1=c2=2.0;CLPSO算法中ω∈[0.9,0.4], c1=c2= 1.49445;A-CLPSO算法中ω∈[0.9,0.4], c1=c2=2.0;AISCLPSO算法ω∈[0.90,0.4],c1=c2=1.49445。通过辨识算法搜索辨识参数值寻优本文的适应度函数表明,ITAE优化法是系统绝对值误差和时间的乘积积分。适应度函数定义为ITAE优化法是由系统绝对值误差与时间的乘积的积分来表示。该函数如式:
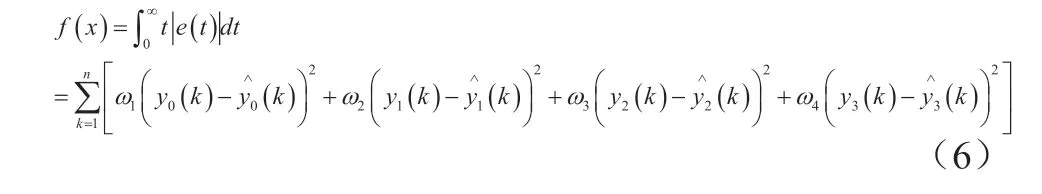
t-test是区分两种算法优劣的统计方法,当t值为正时,算法1的寻优性能优于算法2。相反,算法2的性能优于算法1。从数理统计t分布表中可以看出,t>0表明算法1的性能优于算法2。t=0表示算法1的性能与算法2的性能相同。
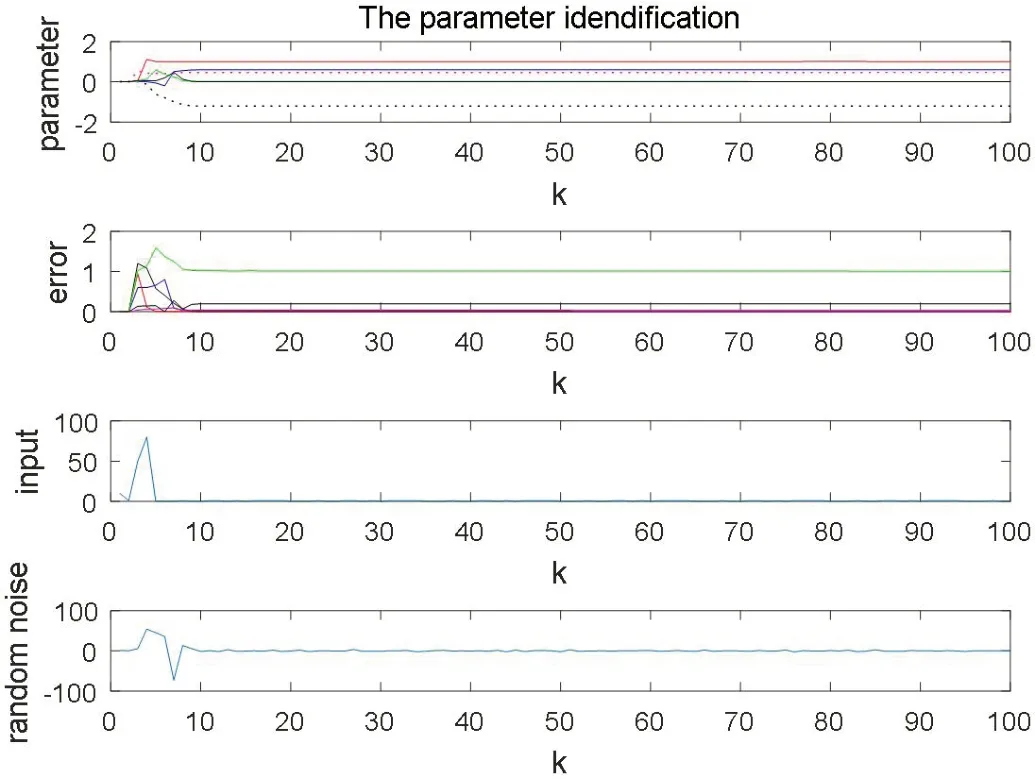
图5:参数辨识曲线
图4和表1显示t=2.06该算法1的性能比算法2的性能具有98%的可靠性。结果表明,该算法的T值和其他四个参数均高于2.06和CLPSO算法。该算法比其他算法更有效。其次,ITAE性能指标用系统的绝对值误差和时间的乘积积分表示,反映了从时间t=0到稳定的整个响应曲线的形态定义,因此比较准确。通过Matlab/Simulink仿真各智能算法的目标函数曲线,可以看出AIS-CLPSO算法的ITAE性能指标数值最小,最准确。
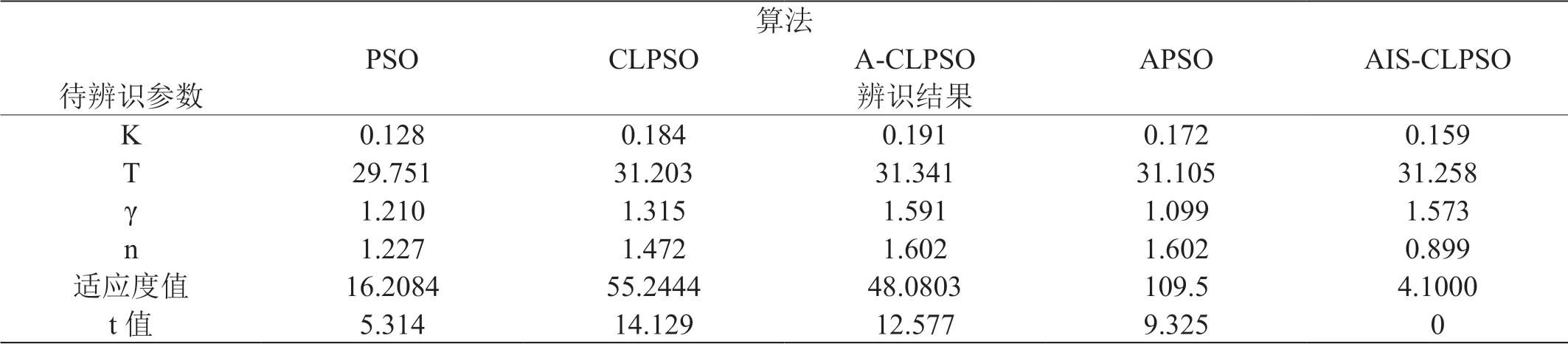
表1:几种算法的倒立摆系统的多参数辨识结果对比表
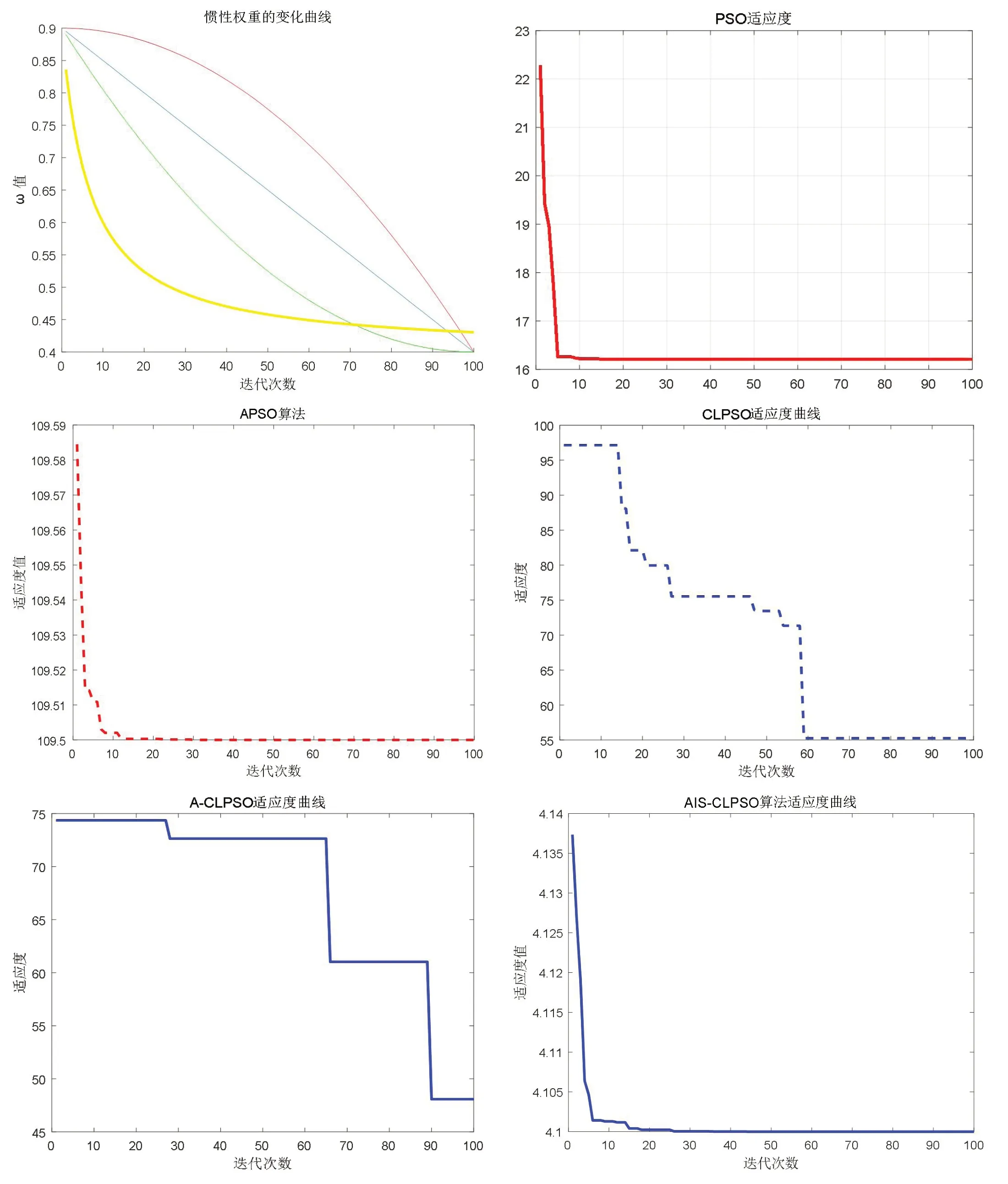
图4:多种算法参数辨识仿真图
在表1中,将AIS-CLPSO算法识别的参数导入到立式3.3中,得到倒立摆系统的分数阶模型:
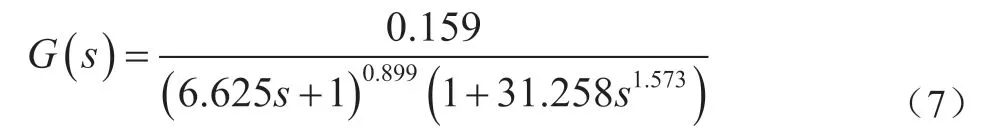
图6和表1中,在给定误差的理想状态下,该分数阶系统的响应曲线与实际系统的响应几乎一致。这证明该喷水系统在研究倒立摆系统时,可以用描述该系统的数学模型进行仿真实验。
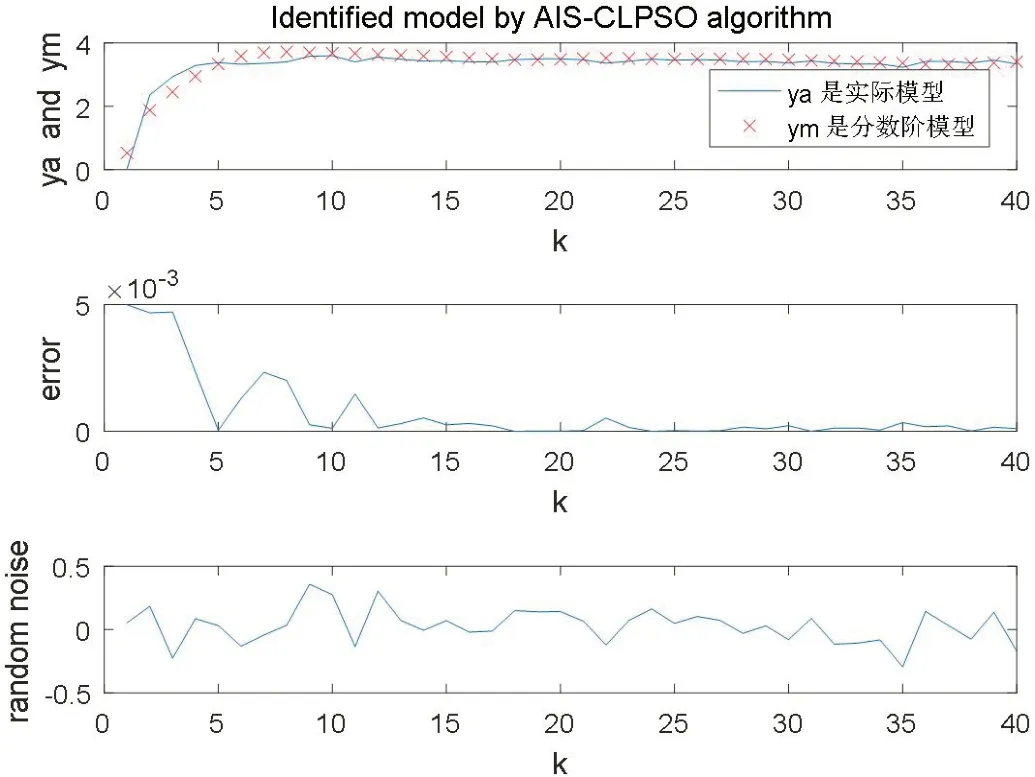
图6:AIS-CLPSO算法辨识模型与实际输出模型比较图
5 结论
本文针对整数阶数学模型失真于真实模型的问题,基于倒立摆系统为模型,分别使用五种智能算法辨识其参数,并采用目标函数和t-test概率评价这两种评价方法分析算法,得出了最优的一组参数数值,从而建立了其分数阶数学模型,并通过实验仿真验证该模型与真实模型的对比效果。

