经纬仪角度测量精度评价方法及测量不确定度评定
金挺 王瑛辉
(浙江省计量科学研究院 浙江省杭州市 310018)
经纬仪是一种由三个轴系(横轴、竖轴、视准轴)和两个圆分度标准(水平度盘和竖直度盘)组成、通过轴系的旋转带动圆分度标准器示值的变动来测量空间方位角的精密计量器具,在大地测量、工程测量和工业测量等领域中得到广泛的应用。作为测绘行业最为经典的测量仪器,一直以来都是以测绘学误差理论为基础来对经纬仪的计量性能进行分析评定,普遍都用“一测回测角标准偏差”作为评价经纬仪角度测量精度的唯一手段,随着经纬仪应用领域越来越广,这种单一评价手段所体现出的问题和缺陷也越来越显著。近十多年来,国内也陆续有学者针对经纬仪计量检定提出了角度示值误差或分度误差[1-4]的概念,但一直未被生产企业和计量检测机构实际采用,在一定程度上导致产品生产者、计量工作者和使用者在经纬仪测角精度认知上的混淆和脱节。本文从“一测回测角标准偏差”的来源和定义、测量误差原理及经纬仪测量误差构成等几个方面,同时结合经纬仪不同的用途,来分析探讨更为合理的经纬仪角度测量精度评价及不确定度评定方法。
1 测量误差与实验标准偏差
对于计量工作者来说,在日常的计量工作中必须要正确地理解测量误差中的一些基本概念。根据文献[5]中的介绍,首先从测量误差原理上来说,测量误差是指测量结果与参考值(标准值)之间的差值,测量误差包括系统误差、随机误差和粗差,在分析测量结果时都会先剔除粗差,因此测量误差一般只包含系统误差和随机误差;其次,测量不确定度是说明被测量分散性的参数,并不是说明测量值是否接近真值。一般在评定测量不确定度时,由系统误差(效应)引入的不确定度分量根据经验或其它信息假设的概率分布按照B类非统计方法进行估算;由随机误差(效应)引入的不确定度分量根据一系列测得值的统计分布按照A类统计方法进行估算,在实际测量过程中一般都采用有限次测量的数据得到的标准偏差的估计值来表征测得值分散性,称为实验标准偏差,一般都采用贝塞尔公式[6]进行估算。

如果在相同条件下对被测量x进行m组测量,得到一系统测得值其算术平均值的实验标准偏差采为:
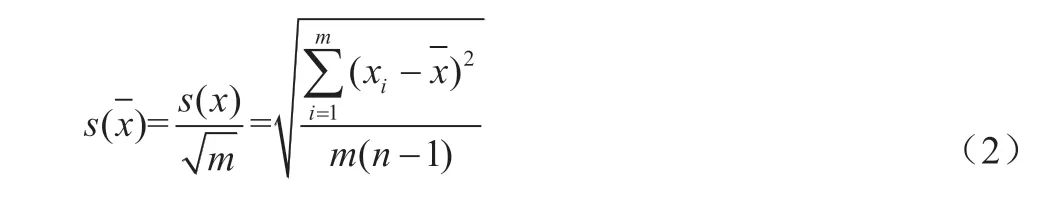
2 一测回测角标准偏差
由于经纬仪具有水平和竖直两个方向的角度测量功能,因此“一测回测角标准偏差”包括“一测回水平方向标准偏差”和“一测回竖直角测角标准偏差”。 “一测回测角标准偏差”起源于控制测量学,其定义可参阅其它文献[7,8],现行的计量规范[9]和产品标准[101]均依据“一测回测角标准偏差”的大小来对经纬仪进行分级。以“一测回水平方向标准偏差”为例,检定规程和产品标准中提供了两种测量方法,分别为“多目标法”和“标准角法”,其中多目标法的数学模型为:
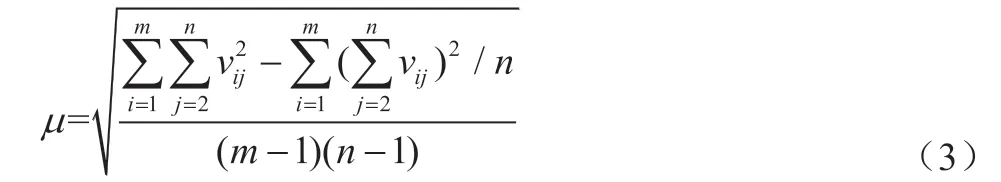
式(3)中:
μ—一测回水平方向标准偏差;
m—测回数;
n —照准目标数;
vij—各目标方向值相对于m测回平均值的偏差。
标准角法的数学模型为:

式(4)中:
μ—一测回水平方向标准偏差;
m—测回数;
n—受测点数;
φij—各方向值残差。
要理解这项指标参数的含义,首先要明确两个概念,分别是“一测回”和“标准偏差”。其中“一测回”是指用经纬仪正镜(盘左)和倒镜(盘右)两个位置对同一目标进行测量,“标准偏差”是衡量一组测量值偏离其算术平均值的程度的指标。从公式(3)和(4)中可以看出,无论是 “多目标法”还是“标准角法”, “一测回水平方向标准偏差”的测量结果都是评价测量值间离散程度的指标,其中的区别在于“标准角法”借助了外部提供的参考标准,其测量结果为外符合精度或精确度;而“多目标法”是将同一个目标各个测回方向角值的平均值作为该目标方向角最或然估值,其测量结果为内符合精度或精密度。不管是外符合精度还是内符合精度,其结果都是在不考虑系统误差影响的情况下对一组测量值通过实验统计方法进行估算的误差影响分量,这与实验标准偏差的定义是一致的,其数学模型与公式(2)也是对应的。
经纬仪国际ISO标准[11]中对“一测回测角标准偏差”参数测试的目的和意图进行了详细的描述,其核心的含义就是该参数不建议作为经纬仪指标性能全面的性能评价试验结果,而是可以看作是角度误差测量结果不确定度评定过程中的一部分。因此,“一测回测角标准偏差”并不是真正意义上的角度测量误差,不能作为测角示值误差的概念来使用。
3 角分度误差
多年以来,国内有多位专家学者就如何融合测绘学和计量学误差理论间的分歧进行了研究,如武汉大学的叶晓明教授[12]发表了多篇相关学术论文来阐述其观点。其实不管是测绘学还是计量学,其测量误差理论其实并没有结构性上的矛盾,只是大家都忽略了一个最基本的问题,就是在提出相关理论的时候没有充分考虑经纬仪实际应用场景。比如在三角测量、三边测量、边角测量、精密导线测量等大地测量的应用上,由于无法找到真值或参考标准值,一般均采用方向观测法、分组方向观测法、全组合测角法等测量方法对导线网精度进行估算,采用的是测回法的测量模式,这时就需要用一测回标准偏差来评价仪器的精度;而在普通的工程测量和工业测量工作中,比如:地形测图、施工放样、机械安装等,一般均采用的是半测回的测量模式(即盘左或盘右单面测量),这时就不存在一测回的概念了,再一味地用“一测回测角标准偏差”的大小来评价仪器的性能就不合适了。在经纬仪实际应用中,经常会有用户将“一测回测角标准偏差”当作经纬仪的测角示值误差来使用,混淆了两者之间的概念,这也有目前经纬仪测角精度评价方法给用户带来的误导的因素存在。
在很多场合,我们往往需要知道仪器自身的误差,也就是通常意义上说的纯仪器误差,纯仪器误差一般由仪器的结构设计和加工装配工艺等因素确定,独立于仪器的测量方法和过程。根据经纬仪的结构原理[9],其仪器误差主要由度盘部分的误差、望远镜部分的误差、读数设备部分的误差、轴系部分的误差和安放设备部分的误差等组成,是体现在半测回状态下的测量误差。纯仪器误差不同于仪器测量时所得结果的精度,一般仪器测量成果的精度与测量方法和测量重复次数有关,它往往不是唯一的一个结果。例如在水平角测量中,仪器的横轴与竖轴的不垂直度误差在半测回方向值(或角度)中不能消除,而在一测回方向值中能够消除;度盘直径系统误差在一测回测量中不能消除,二个测回平均值中(度盘换置90°)能部分消除,而六个测回的平均值中(度盘换置30°)则几乎全部消除。检定规程和产品标准正是应用这种方法进行检测,不同等级的仪器对测回数的要求是不一样的,这里的测回数可以理解成是重复测量次数,目的就是为了尽量消除测量过程中系统误差的影响。
为了能够更全面地表征经纬仪的计量特性,需要得到能真实反映经纬仪角度测量误差的指标。经纬仪作为传统的角度计量器具,其提供的主要示值是角分度值。考虑到其工作原理与多齿分度台相近,参照多齿分度台检定规程[13]中的计量特性,同样可以用角分度误差来表征经纬仪角度示值的准确度,具体的测量方法为:通过具有满足准确度要求的角分度标准器在全圆范围内给出一组标准角分度输入值,将经纬仪度盘的角分度输出值与输入值一一对应进行比较,可得到一组角分度误差值,取其中最大值和最小值之差作为测量结果,即最大角分度误差。本文作者选取了数十台目前市场上常见的经纬仪(包括全站仪),对应“一测回水平方向标准偏差”和“水平方向最大角分度误差”参数的测量结果进行分析比较,实验数据如表1所示,统计对比图如图1所示。
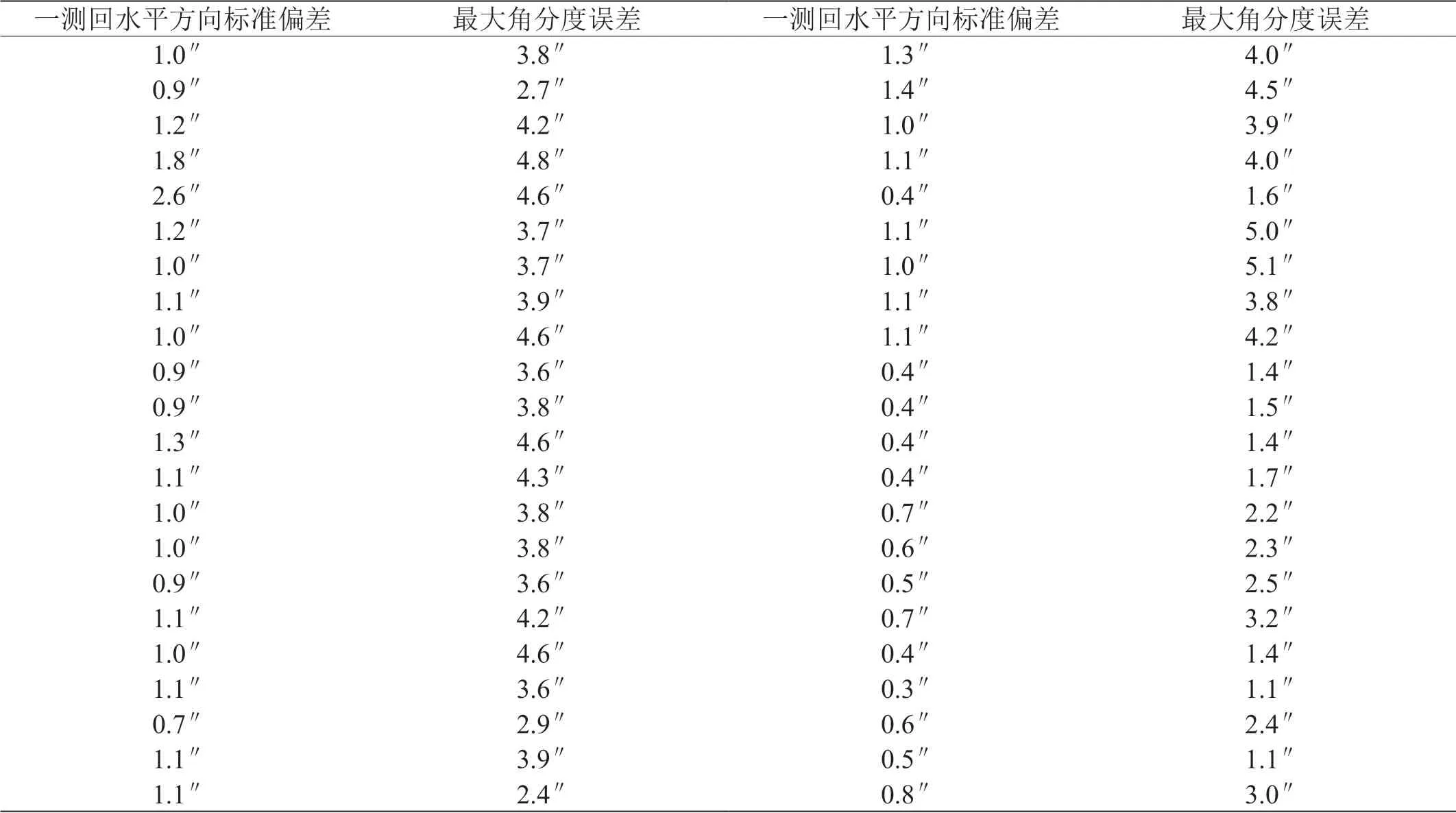
表1:实验数据
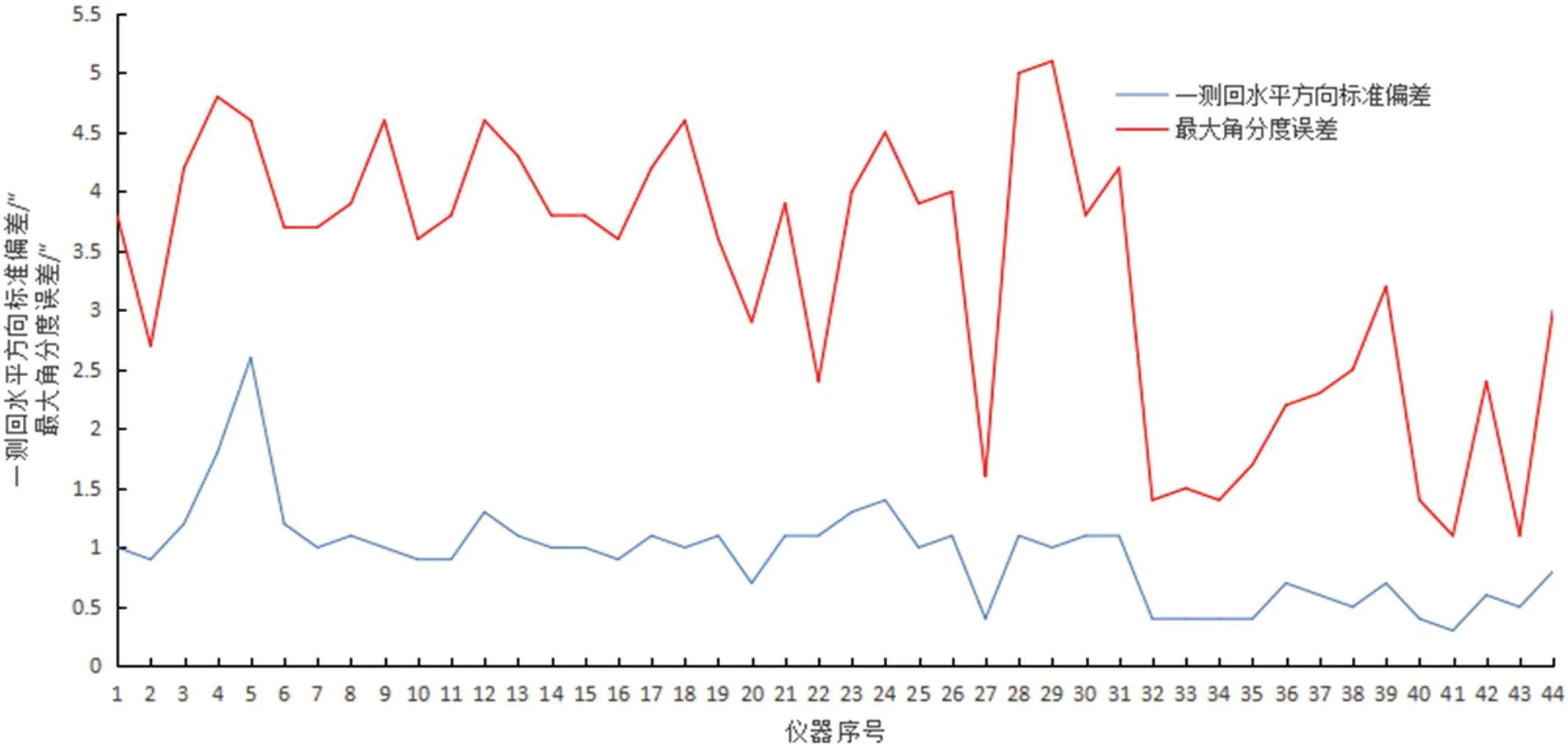
图1:统计对比图
由以上的图表可以很直观地看出“一测回水平方向标准偏差”和“最大角分度误差”间的差异,可以达到数倍的关系。鉴于一直以来国内外的标准规范均单一地按照“一测回测角标准偏差”的大小来对经纬仪进行分级,生产企业也都按照此标准来标注仪器精度,这样不可避免地会对用户造成困惑,因此角分度误差的引入可以更好地解决用户在不同应用领域中对仪器的选择。
4 测量不确定度评定
通常测量结果的好坏用测量误差来衡量,但是测量误差只能表现测量的短期质量,测量过程是否持续受控,测量结果是否能保持稳定一致,测量能力是否符合生产盈利的要求,就需要用测量不确定度来衡量。测量不确定度从词义上去理解,可以看作是对测量结果可信性、有效性的怀疑程度或不肯定程度,是定量说明测量结果的质量的一个参数。
对于如何合理地选择经纬仪计量参数进行测量结果不确定度分析评定是困扰广大计量工作者多年的一个问题。近些来,国内学者发表了不少关于经纬仪“一测回测角标准偏差”不确定度评定相关的学术论文[14-18],也是目前国内众多计量工作者在日常计量检定工作中常用的评定方法。但是根据测量不确定度的定义以及“一测回测角标准偏差”的含义,笔者认为:“一测回测角标准偏差”本身就是一个通过重复测量得到的值,是表征经纬仪在全圆闭合测量过程中各个测量点角度测量误差分散性的量,其测量结果应该视为经纬仪测角示值误差测量结果中由随机效应引入的误差来源分量,而不应再单独对“一测回测角标准偏差”进行不确定度评定。本文以水平角分度误差为例来分析测量不确定度误差分量来源和评定方法。
4.1 测量方法
检定经纬仪角分度误差采用标准角比较法进行测量。将多齿分度台置于零位,转动照准部对准平行光管目标,使仪器的水平度盘置零,顺时针旋转照准部一周,望远镜照准平行光管目标,正镜读数。多齿分度台按预先布点逆时针方向旋转到第2位置,经纬仪照准部以顺时针方向旋转并照准平行光管目标,正镜读数。然后以同样方法检定3、4、…,n位置,最终回到零位。望远镜翻转180°,逆时针方向旋转照准部照准目标,倒镜读数,多齿分度台顺时针旋转到第2位置,经纬仪照准部逆时针旋转照准目标,依次检定各位置,最终回到零位。
4.2 数学模型

式(5)中:
xi—各受检点的方向角测量值;
4.3 灵敏系数
xi的灵敏系数。
4.4 输入量的标准不确定度的评定
4.4.1 由测量标准引入的误差分量u1
检定水平角分度误差时采用多齿分度台作为测量标准,检定规程上要求多齿分度台的最大分度间隔误差≤0.3″,可以作均匀分布处理,则由其引入的不确定度分量为:
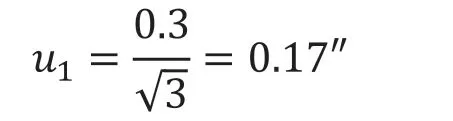
4.4.2 由被测对象引入的误差分量u2
由被测对象引入的误差来源主要包括经纬仪的安装误差、整平误差、照准误差、读数误差等,这些误差影响分量可以合并用重复性测量的方法来得到,可用实验标准偏差即“一测回水平方向标准偏差”来表示。按照经纬仪检定规程中的要求,各准确度等级经纬仪 “一测回水平方向标准偏差”的限差分别为:DJ07级:0.6″、DJ1级:0.8″、DJ2级:1.6″、DJ6级:4.0″,因此由被测对象引入的不确定度分量为:
DJ07级:u2=0.6″;DJ1级:u2=0.8″;
DJ2级: u2=1.6″;DJ6级:u2=4.0″。
考虑到各输入量彼此独立,因此由以上两项合成后的合成标准不确定度uc为:
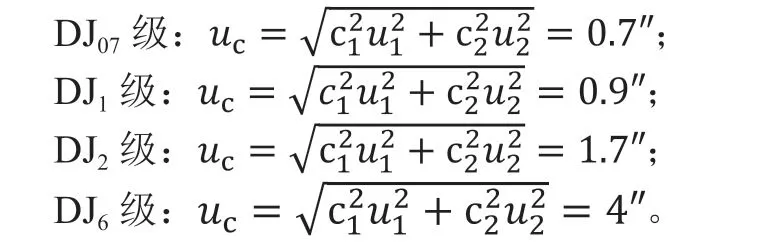
4.5 扩展不确定度
取包含因子k=2,则扩展不确定度为:
DJ07级:U =0.7×2=1.4″;DJ1级:U =0.9×2=1.8″;
DJ2级:U =1.7×2=3.4″;DJ6级:U =4×2 = 8″。
5 结论
基于本文以上的分析和论述,“一测回测角标准偏差”是经典的测绘学误差理论导出的量,适合在控制测量上的应用,但不能完全符合其它一些工程测量误差传递原则。作为国家规范和国家标准等基础性规范性文件,不能只局限于指导某个特定行业或领域的应用,其内容需满足各行业各领域的使用要求。因此综合 “角分度误差”和“一测回测角标准偏差”来判定经纬仪准确度等级能更有效地评价经纬仪角度测量精度,更好地指导日常计量检定工作和测量不确定度评定。

