基于C#的滚动轴承负荷分布计算软件开发

刘志斌, 张少轩, 苏文文

（上海市轴承技术研究所， 上海 201800）

引言

对于滚动轴承而言，套圈滚道与滚动体的法向接触载荷为滚动体主要的工作负荷，此负荷称为滚动体负荷[1]。轴承工况是接触负荷的主要影响因素，此外，接触负荷也受轴承结构及轴承材料等影响。当轴承尺寸确定后，轴承在特定载荷下，求解内部各滚动体受载分布情况即轴承负荷分布求解问题。

低速运动轴承按静载荷计算的负荷分布结果能较好地反应出轴承实际的负荷分布情况。轴承的负荷分布计算可为轴承的承载能力、应力分析及后续的疲劳寿命计算提供基础[2]。

就球轴承负荷分布求解过程而言，其计算公式繁多且复杂，并涉及到多次插值和迭代，手工计算极易出错[3]。本文以提高计算效率为目的，开发出轴承负载分布计算程序，降低计算出错概率，便于对轴承进行更深入的研究。

1 理论分析

以受纯径向载荷的轴承为例，根据赫兹接触理论，滚动体接触负荷与其变形关系有[1]

式中：Qq为第q 个滚动体与滚道接触负荷；n 为与轴承结构相关的系数；δq为内外圈总的弹性变形；Kn为负荷变形常数。

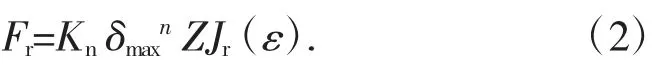
式中：Fr为径向轴承径向载荷；δmax为滚动体最大变形量；Z 为滚动体数目；Jr（ε）为径向载荷积分值。

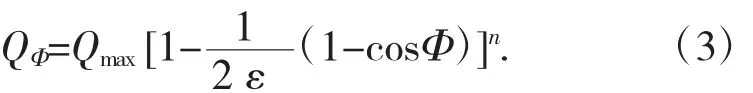
式中：QΦ为不同方位角滚动体载荷；ε 为径向载荷积分常数；Φ 为负荷分布角；Qmax为滚动体最大载荷。

2 软件设计流程

程序设计大致流程如下：为方便数据的统一管理，使用MySQL 数据库对相关数据表进行存储，为实现其过程，需在IDE（集成开发环境）下引用MySQL相关的类库；在.NET 平台下使用C#连接MySQL 数据库对计算公式编写代码，提取方法并封装，方便计算公式的重用，同时提高其程序安全性；使用WPF 技术开发图形界面[4]，图形界面主要功能包括轴承结构选取、载荷类型选取、参数输入、计算结果显示等。

在程序计算过程中，程序通过用户输入的轴承尺寸参数先对中间变量进行计算，获取当前尺寸结构下轴承的曲率和、曲率差及沟曲率半径等中间变量值。然后根据中间变量计算得到不同角度下滚动体的负荷大小。

3 程序运行效果展示

3.1 计算说明

为保证计算程序界面的简洁性，将轴承选取界面和计算过程界面放置于不同窗体之中。

在程序主界面，可选择轴承类型和载荷类型。程序可计算深沟球轴承、圆柱滚子轴承和角接触球轴承在纯径向受载或径轴向联合载荷下的滚动体负荷，见图1。

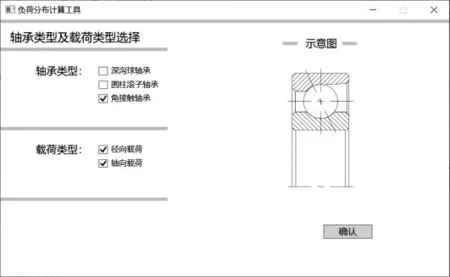
图1 轴承及载荷选取

在确定计算类型后需输入轴承负荷分布计算过程中所必需的尺寸，如滚动体直径、滚动体数目、沟曲率半径等。在手工计算过程中，因载荷积分值与载荷积分常数值需多次数值迭代和线性插值。本文利用计算机计算的高效性对迭代法进行简化，采取在坐标轴上线性等分找零点的方式获取载荷积分值与载荷积分常数值。利用参数k 来控制计算精度（k 为零点范围内坐标轴的等分数），在计算机计算与手工计算的对比计算后可知此法能保证较高计算精度，同时若需提高计算精度，只需适当提高k 值即可。

3.2 算例分析

选取7218 型角接触轴承进行负荷分布计算[5]，轴承部分尺寸见图2 中的输入参数值。

对于系数k，其取值越高，计算精度越高，但计算速度更慢，为平衡精度与计算速度，k 取200。程序计算结果如图2 所示，对于最大滚动体，其计算结果与手工计算结果（6 571 N）[5]误差仅为0.26%，其余滚动体的相对误差也很小，程序计算结果与手工计算结果对比如表1 所示。考虑到程序计算和手工计算的舍入精度不同，可认为计算软件计算的结果准确。对于不受载的滚动体，程序以“NaN”显示。同时由表1 可知，角接触球轴承在承受径向和轴向联合载荷时，随着方位角绝对值的增大，其载荷逐渐减小，符合角接触轴承在承受径轴向联合载荷下的基本规律。

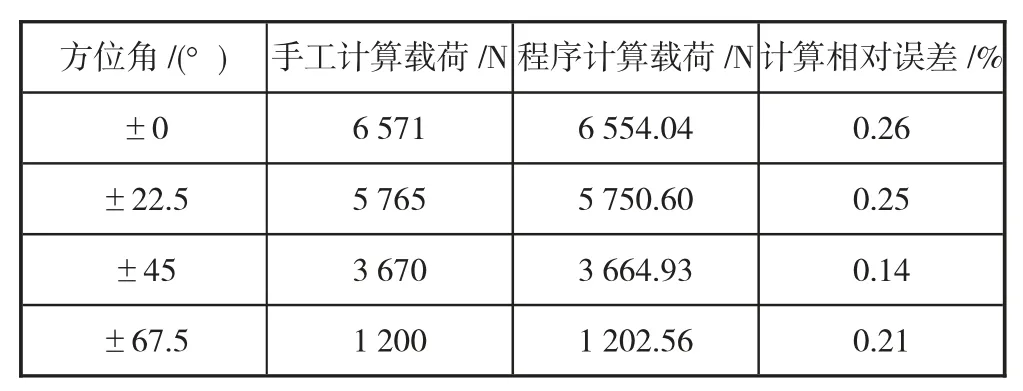
表1 手工计算与程序计算结果对比

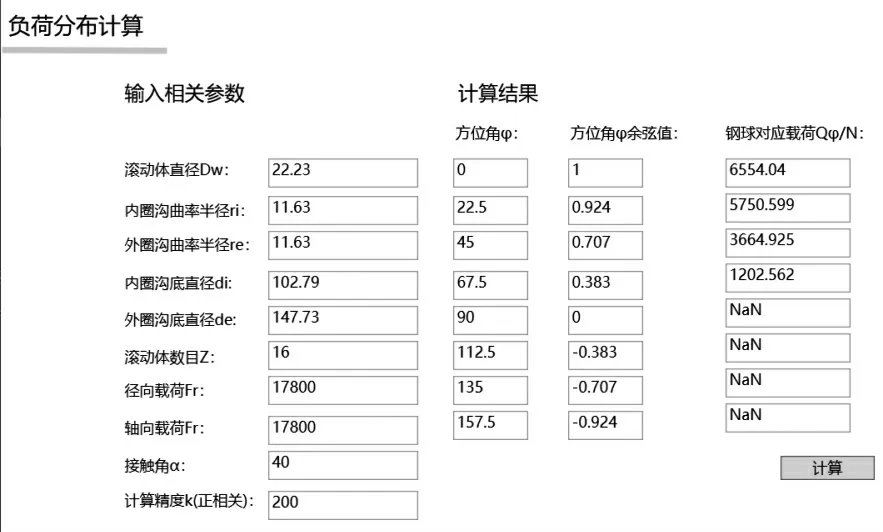
图2 负荷分布计算

4 程序应用前景

轴承在工作中其所受载荷往往不确定，为验证轴承是否满足当前工况条件，需对轴承的最大接触负荷进行校核。若接触负荷大于当前材料下给定的极限应力值，则需考虑对轴承结构进行优化或对轴承材料进行更换。

根据赫兹理论计算接触应力时，必须先对最大受载滚动体所受的载荷进行计算。而在计算滚动体载荷时，又需对前置参数（如总曲率、内外圈对应的沟曲率半径系数等）进行准确的计算，各个参数间关联密切，需保证所有参数代入计算的准确性。在以往的手工计算中，极易把内外圈相关参数混淆，导致计算结果出错，而在中间计算过程中又很难自我校正，此时大大体现出了程序自动计算的便捷性。此外在对轴承结构优化时，只需对尺寸参数中的某一个值进行很小的改动，但手工计算需对所有公式重新计算，程序软件则可快速地获取所需结果。因此，此软件在轴承结构优化过程中及理论研究方面可大大提高计算效率，减少不必要的时间浪费。

5 结语

滚动体负荷分布情况与轴承实际工况和几何结构有着紧密的联系，因其计算复杂，不利于研究轴承几何结构对轴承负荷分布的影响[6]。本文使用C#语言开发了滚动轴承负荷分布计算程序，其能对滚动轴承中最常用的轴承类型（深沟球轴承、圆柱滚子轴承和角接触轴承）的纯径向载荷或径轴向联合载荷负荷分布进行计算，代替了烦琐的手工计算，减少计算出错概率，对轴承的尺寸设计和力学性能研究具有一定的指导意义。