振动盘料斗几何参数的研究与优化

何 贤， 区焕财， 何学文

（1.江西理工大学机电工程学院， 江西 赣州 341000； 2.广东顺德创新设计研究院， 广东 佛山 528318）

引言

振动盘具有简单的结构和可靠的性能，广泛应用于电子和轻工行业，是自动化生产中的常用设备[1]。由于缺乏理论指导，振动盘料斗的设计制造需要依靠经验，并经多次试错完成[2-3]，这使得振动盘的设计费时耗财，而且各个参数的选取不能达到最优，直接影响了物料的进给速度和整个设备的性能功耗。针对这些问题，许多学者做了大量研究：顾平灿[4]研究了不同供料方式下物料进给速度与振幅之间的关系；周伟[5]研究了料槽倾角、振动方向角、频率、振幅对物料输送速度的影响；伍利群[6]对电磁振动给料机上物体进行受力和运动分析，分析了物体的各种运动状态；孙为韬和吕彦明[7]研究了振动料斗料槽的几何参数和给料速度的关系，找出了最佳运动状态下料槽几何参数的设计范围。

以上多是针对振动给料机各参数与物料进给速度关系的研究，而针对如何选取各参数来降低能耗的研究却很少。基于此，本文通过寻找物料向上滑移的临界加速度的最小值来达到降低功耗的目的，建立了优化数学模型，对现有振动盘的结构参数进行了优化。

1 电磁振动盘的结构及其工作原理

振动盘的整体结构如图1 所示，它由料斗、连接块、衔铁、板弹簧、电磁激振器、基座和隔振底脚组成。电磁激振器安装在基座中央，4 组多层板弹簧以一定的倾斜角度均匀分布在基座上，一端与基座固定，另一端与连接板固定，料斗安装在链接板上。料斗底部呈锥形，料道在料斗内部螺旋上升，针对不同的零件的定向需求，可以在料道上设置一些定向机构。

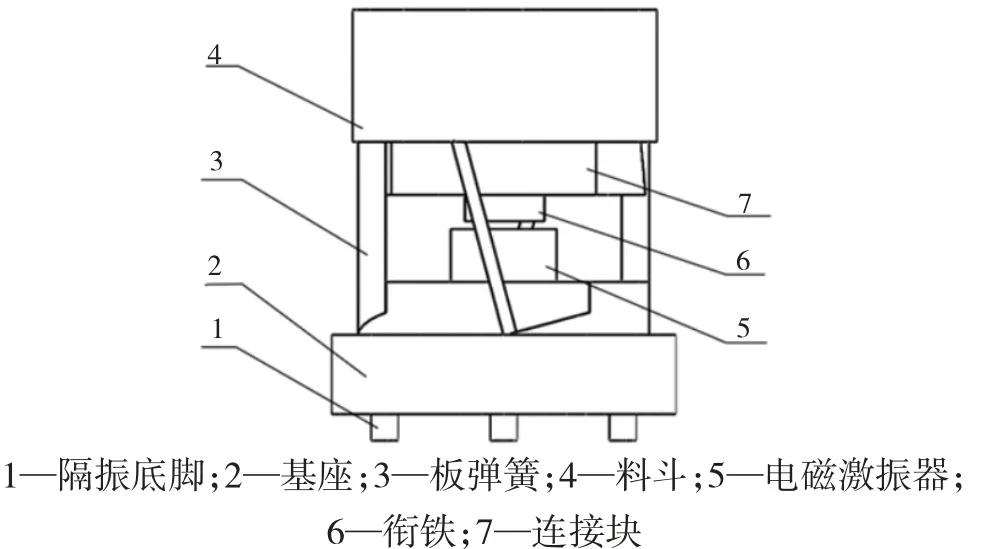
图1 振动盘结构图

振动盘的工作原理是：通电后电磁激振器产生电磁力，该电磁力带动连接板和料斗沿垂直方向运动的同时绕轴线发生扭转运动，同时多层板弹簧吸能产生形变。随着电磁力消失，板弹簧释放能量恢复形变，带动料斗回到原来的位置，如此往复，使得料斗高频微幅振动。料斗中的零件在这种振动的作用下沿螺旋料道向上缓慢移动，实现给料。

2 振动输送力学分析

为了便于分析，截取料斗的一部分简化成如下页图2 所示的形式来对其进行受力分析，从图2 中可以看出，板弹簧的安装角为γ，料斗中料道的螺旋升角为α，振动升角为β。根据受力情况的不同，物料有四种运动状态，即相对静止、相对向前滑移、相对向后滑移和跳跃运动。物料的运动取决于料斗的运动，由机械振动理论得知料斗作简谐振动，假设料斗的位移为S，加速度为 a，则有：

式中：A 为料斗振幅；ω 为角频率。

如下页图2 所示，作用在物料上的力有物料自身的重力mg、物料与料道表面的摩擦力Ff、料道对物料的支持反力FN和惯性力Fa。当料斗受电磁力向左下方运动时，物料受反方向的惯性力，当惯性力沿x 方向的分力大于摩擦力与重力沿x 方向的分力之和时，物料沿料道向上滑移，小于时物料相对料道静止，等于时物料处于临界状态，此时有：

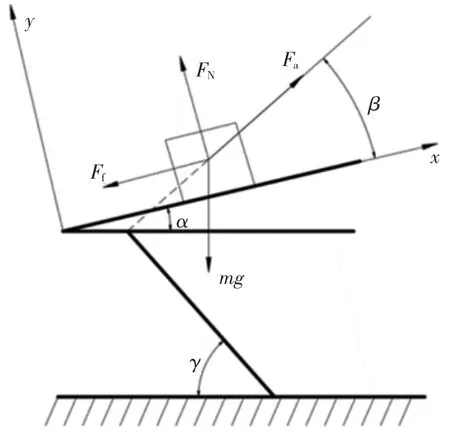
图2 物料受力分析图

式中：μ 为物料与料道表面的静摩擦系数。

由式（3）可知，物料静止时的条件为：

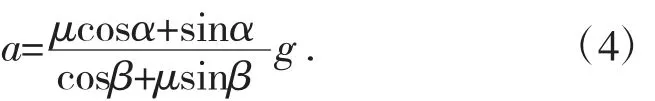
令ax+为加速度沿x 方向的分量，则料斗向下运动时，当 ax+≥acosβ 时，物料向上滑移；当 ax+＜acosβ时，物料相对料道静止。

当电磁力消失，料斗在板簧的作用下沿右上方移动，此时加速度方向改变，同理，可推导出物料向下滑移时的临界加速度：

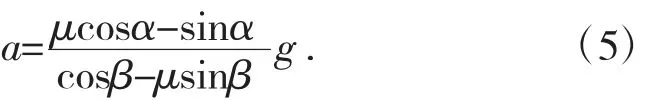
令ax-为料斗上移时的加速度沿x 方向的分量，当 ax-≥acosβ 时，物料向下滑移，当 ax-＜acosβ 时，物料处于稳定状态。

当惯性力沿y 方向的分量大于重力沿y 方向的分量时，物料产生跳跃运动，两者相等时处于临界状态，此时支持反力FN=0，则有：

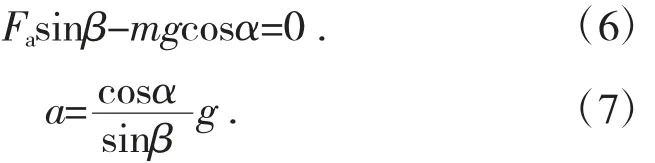
令axo为加速度沿x 方向的分量，ayo为加速度沿y 方向的分量，则：

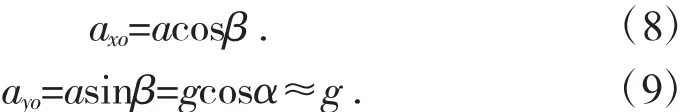
由此可知，当料斗振动加速度沿x 方向的分量满足 axo＞acosβ 或沿 y 方向的分量大于重力加速度时，物料产生跳跃运动。

为了应对财政局的审计，或者为了最大限度地发挥短期效益，部分公司纵容财务人员伪造虚假的资料，使资金流入虚假账户[2]。其他人由于业务水平低而无法准确记录凭证，这样会导致用缺乏真实性的数据进行分析、评估。

3 参数的优化设计

在正常工作情况下，物料向上和向下滑移的临界加速度小于物料跳跃时的临界加速度，且一般有需满足的约束条件ax+＜ax-＜axo，故本文只针对这种情况进行研究。

在振动盘设计时往往根据经验选择料斗的设计参数，使得物料向上滑移的临界加速度偏大，虽然能达到送料的目的，但是振动盘的能耗较高，因此在料斗设计时，应该使振动盘满足送料要求的同时具有较低的能耗。鉴于此，构建了如下振动盘结构优化设计的数学模型，即以料道螺旋升角α 和振动升角β 为设计变量，以物料向上滑移所需的临界加速度最小为目标函数，同时需满足的约束条件有 ax+＜ax-＜axo；设计变量的上下限。

则优化设计的数学模型如下：

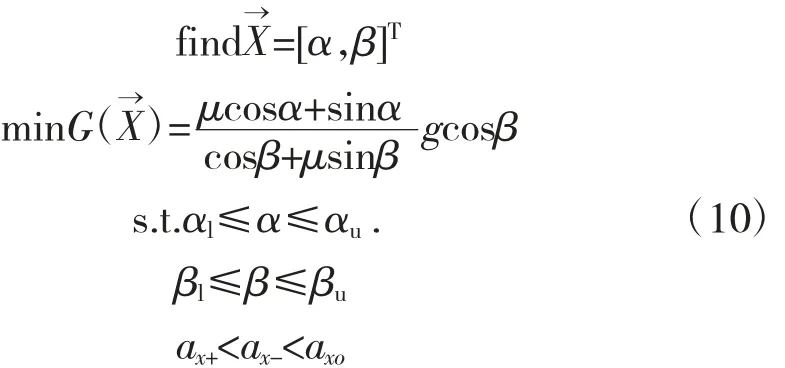
式中：G（X→）为物料向上滑移的临界加速度沿x 方向的分量；αl、αu、βl、βu分别为 2 个设计变量的下限值和上限值。

由于螺旋升角α 和振动升角β 的值不仅与各临界加速度有关，而且还影响着物料的进给速度，如何选取一个合适的范围至关重要，本文根据对物料运动状态的分析，利用MATLAB 编写仿真程序对其速度进行仿真，寻找α 和β 的合理取值范围。

本文采用控制变量法，设g=9.8 m/s2，f=50 Hz，选取振幅为80 μm，摩擦系数μ=0.5，通过改变料道的螺旋升角α 和振动升角β 来研究它们与物料进给速度的关系，仿真结果如图3 所示。

从图3 中可以看出，物料的进给速度随着振动升角的增大先增大后减小；当振动升角固定，物料的进给速度随料道的螺旋升角的增大而降低；当料道的螺旋升角过大且振动升角过小时，进给速度会小于零，即物料无法向前运动，所以应该避免这种情况。

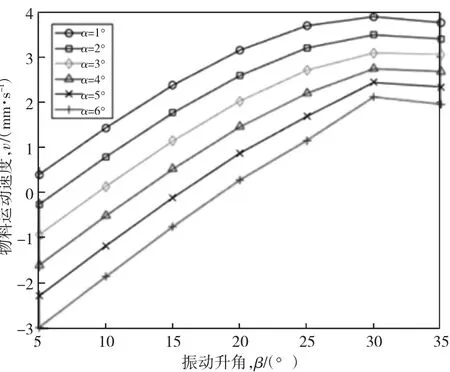
图3 振动升角和螺旋升角与物料进给速度关系图

针对上述分析，合理选取α=1°～4°，β=10°～25°，在此参数范围内进行优化设计既不影响给料又能降低功耗。将给定的各参数带入优化设计模型，则有：

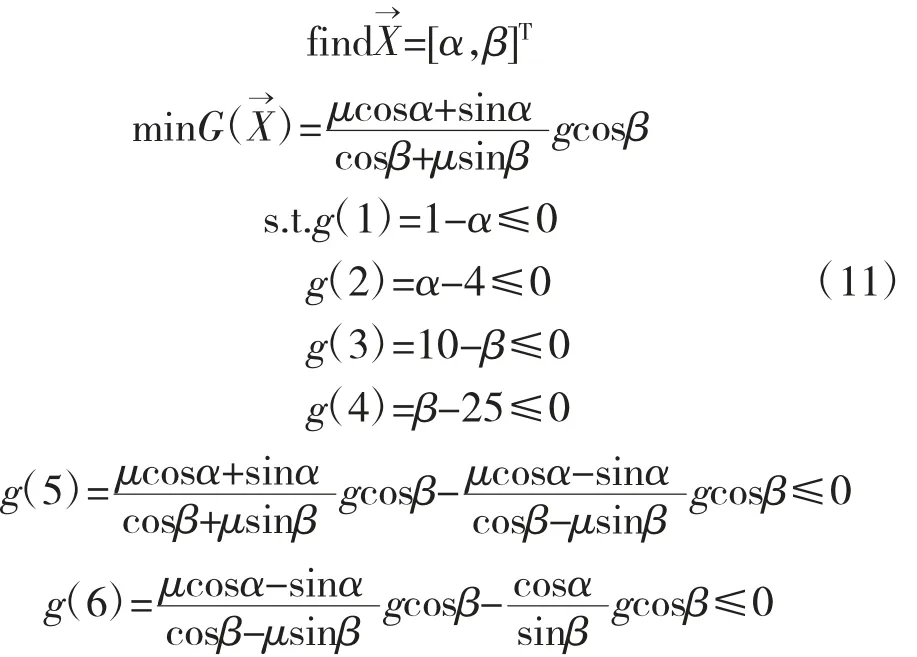
4 优化实例与结果分析

在实验室一条自动化生产线上有一台振动盘，该振动盘能完成送料，但是需要较大的电磁力驱动，能耗较高，本文对其进行优化设计。该振动盘料斗由不锈钢制作而成，输送物料是塑料瓶盖，已知物料与料道间的静摩擦系数是0.3，料道螺旋升角α=3°，振动升角β=20°，优化结果如表1 所示，优化后物料沿料道向上滑移的临界加速度降低了12.2%。

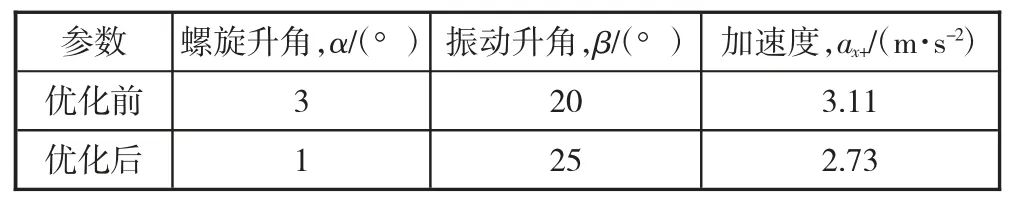
表1 优化前后料斗各参数值

5 结论

1）本文分析了物料四种不同的运动状态，建立了不同状态下的力学方程，得到了物料满足各种运动状态所需的临界加速度。

2）利用MATLAB 编写计算机仿真程序对物料运动速度进行仿真，研究不同的螺旋升角和振动升角与物料进给速度的关系。根据仿真结果，料道的螺旋升角α 越大，料道坡度越陡，物料进给越困难，而随着振动升角β 增大物料进给速度也会增大，但振动升角β越大，板弹簧安装角γ 越小，虽然有利于送料但是会增大振动盘的体积且容易导致物料跳动，所以在设计振动盘时，一般取α=1°～4°，β=10°～25°。

3）为了以最小的激振力来达到送料的目的，从而降低振动盘功耗，以物料向上滑移所需的临界加速度最小为目标函数建立了优化数学模型，并对现有的一台振动盘进行优化，优化后物料向上滑移的临界加速度减少了12.2%，为后续的设计提供了理论指导。