特大桥跨河连续梁施工的物资成本控制模型
周英男
(中铁十八局集团第一工程有限公司,河北 涿州 072750)
在特大桥跨河连续梁施工过程中,物资种类众多,物资成本投入是特大桥连续梁建设成本核算中的重要内容[1-3],在其成本核算中所占比例较大,对特大桥跨河连续梁施工的物资成本进行有效控制是实现其成本控制的重要手段。
成本控制方面的研究较为成熟,杨儒君等[4]提出建立基于BIM技术的施工资源隐性成本控制模型,并通过GA算法实现该模型的求解,但该方法预测的施工资源隐性成本准确度不高,与实际成本预算存在较大偏差;王雁[5]针对地震灾后民用建筑重建工程,在对施工成本进行问题分析的基础上,依据施工各阶段的成本数据信息,利用BIM技术建立其成本控制模型,实现成本控制,但该方法在对施工资源成本进行预测时准确度不高,且无法在规定施工周期完成施工任务。因此,文章提出特大桥跨河连续梁施工的物资成本控制模型,构建特大桥跨河连续梁BIM模型,解决施工成本控制精度低、施工进度滞后等问题,确保施工质量达到预期要求。
1 施工物资成本控制模型
1.1 特大桥跨河连续梁的施工方案
桥墩573#-577#连续梁跨越金堤河,主梁长度为208.5 m。574#墩大里程侧承台角距金堤河边坡顶最小距离1.23 m,576#墩小里程侧承台角距金堤河边坡顶最小距离4.9 m,该桥的总布置图如图1。
特大桥跨河连续梁悬臂法施工流程为:
跨金堤河连续箱梁采用挂篮悬臂现浇法施工,连续梁0#块、边跨直线段采用支架法现浇[6]。悬浇段的、#块外模板采用定型钢模板,边跨现浇段外模采用钢板,0#块、边跨现浇段底模采用钢板,悬浇段底模采用定型钢模板,内模采用小块组合钢模板形式。悬灌段采用菱形挂篮施工,在0#块上安装挂篮主构架,按照顺序施工悬浇段直至合拢段。合拢段施工时先合拢边跨,然后进行连续梁纵向通长束张拉压浆,完成体系转换。
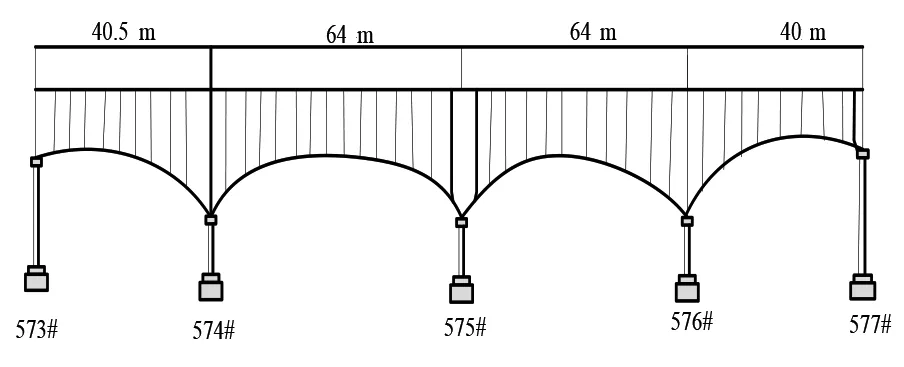
图1 特大桥跨河连续梁的总布置图
1.2 基于BIM的特大桥跨河连续梁全寿命周期施工物资成本控制模型
文章利用BIM技术实现特大桥跨河连续梁的全寿命周期施工成本控制,其成本控制模型结构如图2。
特大桥跨河连续梁的施工成本控制模型结构主要包含以下三部分内容:
(1)数据层。该层为特大桥跨河连续梁的施工物资成本数据库,特大桥跨河连续梁施工各周期内的成本数据均存储在该数据库中,成本数据中包括往期数据、现下施工成本数据[7]。各施工参与方均可通过该数据库实现物资成本数据的传输通信。
(2)模型层。该层由BIM设计模型、施工模型、运行维护模型组成。通过BIM模型可获取特大桥跨河连续梁施工的物资单价信息、定额信息、设计属性和工程量信息以及运算规则等方面的内容。
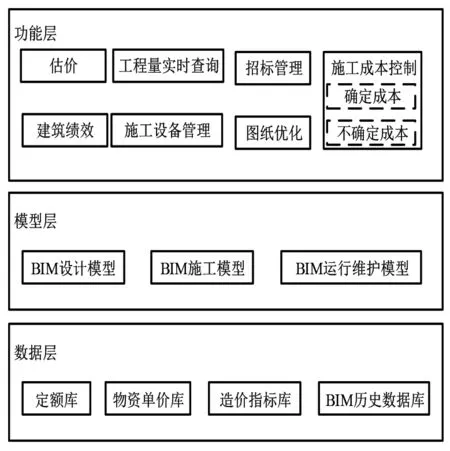
图2 基于BIM的特大桥跨河连续梁全寿命周期施工物资成本控制模型结构
(3)功能层。施工成本控制包括两方面,一方面为基于施工物资利用分进化算法实现确定性成本控制,另一方面为利用BIM的最后计划者体系完成施工过程中的不确定成本控制。
1.3 特大桥跨河连续梁施工BIM模型
文章通过构建BIM模型实现特大桥跨河连续梁施工成本控制,将构建的各专业BIM模型进行整合,对设计中的不合理处进行修正,提高模型质量[8],最后由各施工参与方共同审核各BIM模型,确定BIM模型。特大桥跨河连续梁的BIM模型构建流程如图3所示。
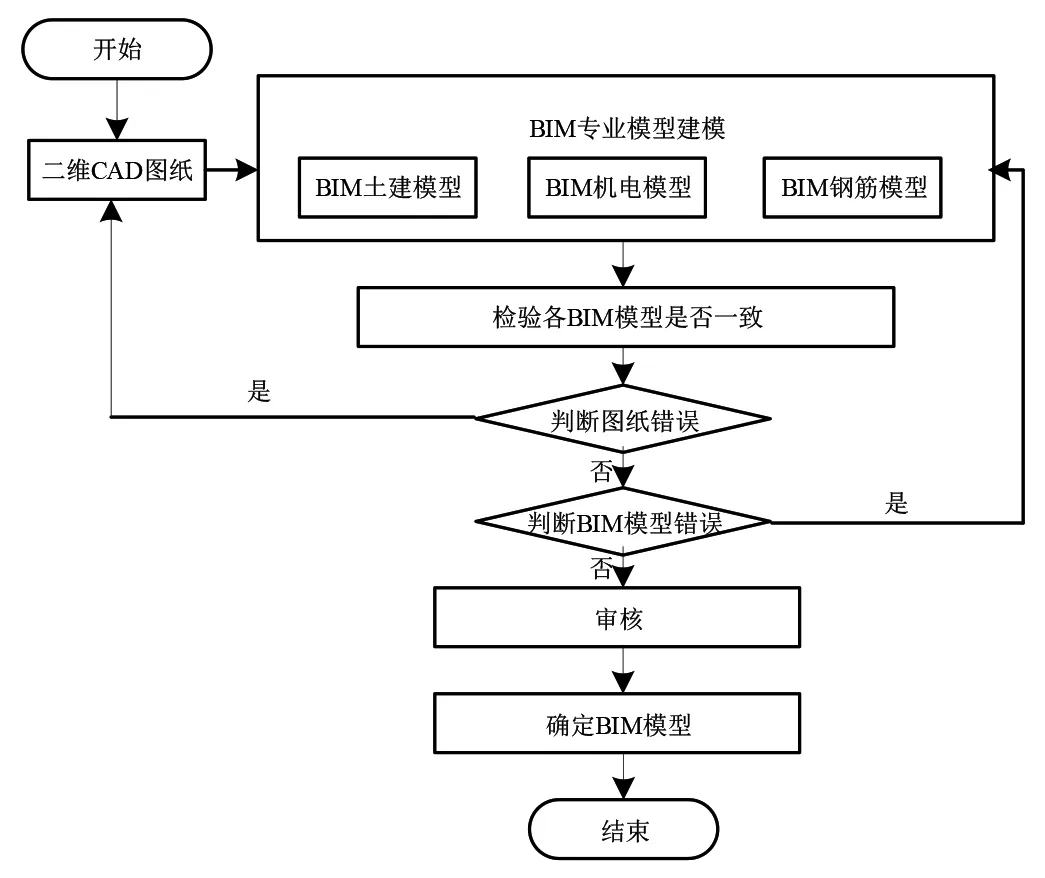
图3 特大桥跨河连续梁的BIM模型
1.4 施工物资确定成本控制模型
以工程在预定施工周期内圆满竣工为首要目标,通过获取施工成本最小化的物资分配结果,构建物资确定性成本控制模型[9]。建立模型需设定以下条件:
条件1:在施工时,各施工阶段、施工工序所需物资用量额度相同,并对施工物资可使用时间进行预先设定。
条件2:特大桥跨河连续梁开始施工后,各工序按计划稳定执行,无停工状况。
条件3:上下工序连续执行,后续阶段需在上一工序执行完毕后方可继续。
按照上述条件,将施工工序实际起始时间作为模型的约束条件进行描述。
设工序为j,上一工序为j-1,则施工项目的实际施工起始时间为:
TRj∈int+,j=1,2,3,…n
(1)
该时间为整数,且大于0。以0为起始端,连续梁施工周期表示为TR0=0。当前一工序施工结束后方可对下一工序进行施工,表示为:
TRj-1+Hj-1≤ERj
(2)
式中:施工周期为Hj,该工序提前执行时的起始日为ERj。特大桥跨河连续梁施工工序实际起始时间约束条件描述为:
ERj≤TRj≤LRj
(3)
式中:该工序可允许的最迟施工日为LRj。
在上述约束条件约束下,构建施工物资确定成本控制模型,获得最优物资分配策略。
施工各物资需求量可通过施工物资成本进行描述。设xn为日物资需求量标准差,最优物资分配策略即当xn取最小值时的分配方案。xn可通过下式进行描述:
(4)
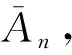
特大桥跨河连续梁施工时,各施工物资分配的不均衡性的极小值表示为minW,文章以此为优化目标,实现施工物资确定性成本最小化。
(5)
式中:λn为各施工物资的权重系数,可通过模糊层次分析法、专业人士评分法确定。
由此完成施工物资确定成本控制模型。
1.5 施工物资确定成本控制模型求解
差分进化算法适用于连续不间断问题的计算,因此文章利用差分进化算法对特大桥跨河连续梁施工的物资成本控制模型进行求解,获取确定物资成本的最小值,实现最佳特大桥跨河连续梁施工确定物资成本控制。文章在应用该算法进行求解时,需将施工工序进行连续性转换[10-11],即将一个施工工序定义为一个染色体,依据其序号及编码数量,按从小到大顺序对其进行排列。
1.5.1 变异操作
为了使成本控制模型求解出的最佳个体具备完整信息,提高进化率,进行变异操作。对种群进行初始化,N为候选个体(施工工序)的种群规模,G为施工工序的向量转换维度。对种群中的不同施工工序向量进行筛选,获得变异个体。变异操作可通过下式进行描述[12]:
(6)
其中:i=1,2…N,缩小因子表示为H;rand为区间[0,1]的任意值;r1、r2、r3的取值范围为[1,N],且r1≠r2≠r3;Xbest(t)为此刻的最佳个体。
1.5.2 交叉操作
该步骤是通过对变异个体、初始个体含有的信息进行互换,产生新候选个体。新候选个体中同时包括变异、初始个体的部分信息,交叉操作可用下式进行描述:
(7)
其中:i=1,2,…N;j=1,2,…G;交叉概率表示为Cr;rand(G)的取值区间为[1,G],且为整数。
1.5.3 选择操作
对初始个体及备选个体的适应度值进行求解[13],选择最佳适应度值作为目标函数,并作为后代个体,从而实现种群的迭代遗传,具体可通过下式进行表达:
(8)
其中:i=1,2,…N。
采用改进差分进化算法求解最优物资成本的步骤如图4所示。
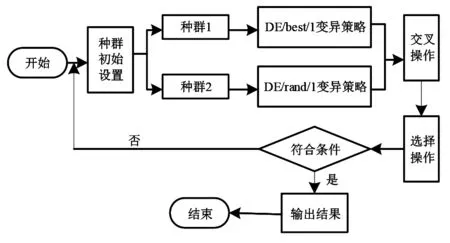
图4 改进差分进化算法的最优物资成本求解流程
1.6 基于BIM的最后计划者体系控制不确定性成本
最后计划者体系是指在施工项目执行前需对其工作流程、多级交互等进行预先规划,使各项条件均满足要求,最大程度地减少干扰因素对施工项目的影响[14]。各方施工负责人根据其具体施工进展缮制施工计划,并对施工执行情况进行监督与跟踪,实现施工过程的统筹部署,经个人或小组决议后执行具体施工任务,最后计划者体系控制不确定性成本通过BIM技术实现。采用BIM-4D可对施工过程进行模拟[15],并以动画方式进行可视化呈现,最大化减少施工过程中的不确定性因素。利用BIM技术的“碰撞检测”性可有效降低重复施工风险,使施工过程更加高效,减少施工过程的不确定成本。
2 实验分析
以该特大桥跨河连续梁施工项目为研究对象,该连续梁施工总周期为10个月,采用本文方法对物资成本进行有效控制,验证本文方法的成本控制效果。 采用本文方法构建特大桥跨河连续梁的BIM模型,其三维效果图如图5所示。

图5 特大桥跨河连续梁的BIM模型
依据实际工程进度、物资成本确定其实际进度-成本曲线,采用本文方法对不同施工进度下的各物资成本进行控制,控制后的成本曲线与实际施工成本预算曲线进行对比,结果如图6所示。
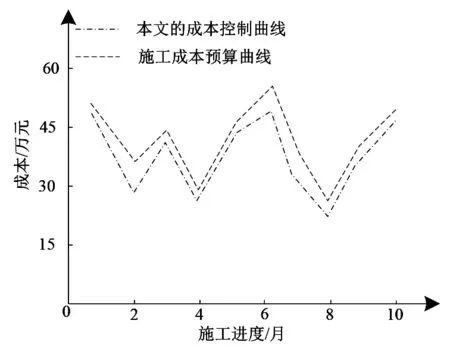
图6 本文方法的成本控制效果分析
分析图6可知,当采用本文方法进行成本控制后,各施工周期的物资成本均有所降低,特别是在施工的第2月、第6月,施工物资成本降低幅度较大。
在对特大桥跨河连续梁进行施工时,施工各阶段制定的计划施工物资预算成本,标记为A,实际已完成工序的物资成本标记为B,通过上述物资成本可对施工进度信息进行判断,当成本B>成本A时,表明特大桥跨河连续梁的施工进度快于计划进度。反之则说明实际施工进度比计划进度滞后。根据特大桥跨河连续梁施工总周期内的成本A、成本B的变化情况,分析其施工进度信息,并与文献[4]、文献[5]方法获得的进度信息进行对比,结果如图7所示。
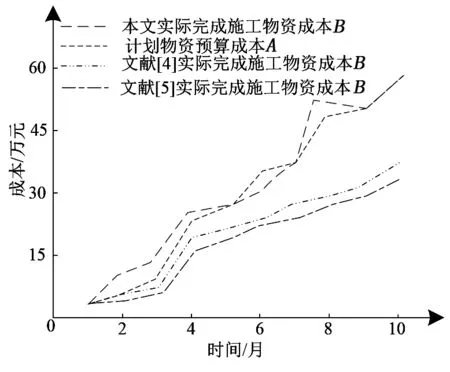
图7 施工进度分析
分析图7可知,本文方法在1月-5月、7月-9月时成本B均高于成本A,说明在此阶段的施工进度均快于计划进度,5月-7月的施工进度低于计划进度,最终在施工总周期内完成施工任务。文献[4]方法的成本B始终低于成本A,且偏差逐渐偏大,说明文献[4]方法的工程进度低于计划进度,无法在计划施工周期内完成施工任务。文献[5]方法同样存在施工进度较慢的问题。由此可说明本文方法可有效提升施工进度。
接近度反映的是二者之间的一致性程度,二者间偏差越小,接近度越高。通过分析本文方法在成本、进度、质量方面与计划预算的接近度验证成本控制有效性,实验结果如图8所示。
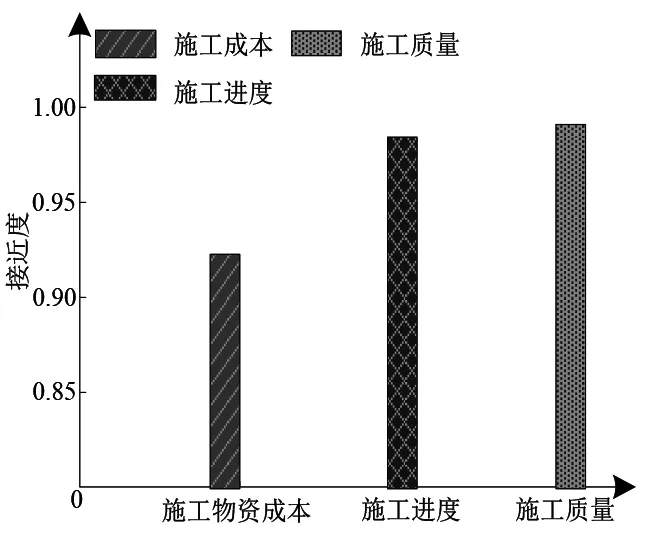
图8 施工过程各接近度指标分析
分析图8可知,本方法在对特大桥跨河连续梁施工进行物资成本控制后,成本、进度、施工质量接近度可达到92.5%、97%、98.5%,说明本文方法可将物资成本控制在预算的92.5%,可节省成本7.5%,施工效率可提升3%,施工质量基本可达到预期效果。实验结果表明,本方法可有效控制物资成本,施工进度满足计划要求,并保证施工质量。
3 结论
以某特大桥跨河连续梁施工项目为研究对象,在该特大桥的连续梁施工过程中,对其施工物资成本进行控制,通过分析物资成本、进度、施工质量的接近度指标分析物资成本控制的有效性,可节省7.5%的物资成本预算,施工效率提升3%,施工质量达到预期要求。

