助飞鱼雷模态振型斜率仿真计算

王升,白治宁,郭君

(中国船舶集团有限公司 第705 研究所,陕西 西安,710077)

0 引言

导弹若未考虑弹体的弹性振动可能导致发射飞行失败,因此,新研制的导弹和运载火箭都会通过振动特性试验测量其结构动力学特性,其中主要的参数就是振型斜率[1-2]。助飞鱼雷与导弹、运载火箭的结构特点相似,其长细比较大,结构刚度较小,在气动力的作用下也会产生变形和弹性振动,将影响敏感元件惯性测量组合的测量精度,甚至会错误地判断全雷的飞行姿态。在研究和设计助飞鱼雷的姿态控制系统时,同样必须考虑全雷的弹性变形影响,通过全雷振动特性试验,获得准确的模态参数以及惯组安装位置的振型斜率作为姿态控制设计输入参数[3],以确保飞行过程姿态能够得到稳定控制。

全雷振动特性参数往往在产品加工后通过振动特性试验获得,在产品研制阶段,惯组安装位置确定和姿态控制设计所需要的模态参数以及惯组安装位置的振型斜率,只能通过仿真分析方法获得。且在新的产品研制模式要求下,通过仿真方法获得准确的振动特性参数尤为重要。目前模态振型斜率的仿真分析在导弹和火箭领域均有研究成果:潘忠文[4]在传统等效梁模型基础上,对局部结构详细建模方法进行了全箭动特性分析及振型斜率的仿真分析;李家文等[5]通过对比2 种振动建模方法,建立了捆绑火箭姿态动力学新模型;祁峰等[6]通过舱段试验完成了精细化建模及修正,进行了全箭模态振型斜率的仿真分析;芦旭等[7]在研究了局部三维有限元精细模型建模方法,并分析了局部连接刚度对振型斜率的影响。

助飞鱼雷因其独特的楔环和分离舱连接结构等特点,与导弹及运载火箭具有明显的区别。文中基于模态分析进行了助飞鱼雷振型斜率的仿真计算,建立了助飞鱼雷全雷三维详细动力学模型,进行全雷模态分析,并计算了惯组安装位置处的振型斜率,比较了发动机满载和空载时的差异。

1 弹性体振型斜率计算原理

对于多自由度一般粘性阻尼结构系统[8],当外部激励为零时,其动力学微分方程为

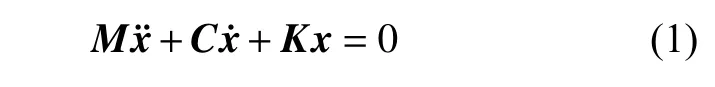
式中:M为质量矩阵;x为位移列阵;C为阻尼矩阵;K为刚度矩阵。

求解上述方程都转化为求解式(2)的广义特征问题,即

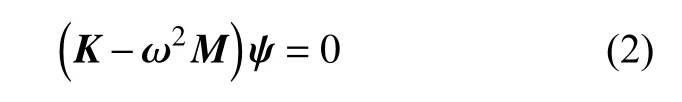
式中:ω为特征值,即弹性体的模态频率;ψ为特征向量,即弹性体的振型。

分析弹性体振动特性时,结构力学中一般基于质量归一化进行计算。但计算姿态控制系统设计所需的振型及振型斜率时,需要按某一参考节点进行归一化处理,假设参考点振型向量中振幅为uj,则相应阶次的振型向量为

2 动力学建模

将助飞鱼雷全雷模型进行简化处理,保留壳体及主要连接结构,如鱼雷中的楔环连接结构、分离舱与鱼雷的止推块结构、分离舱和仪器舱的卡箍结构等,将部分内部安装的零部件简化为质量点。简化后的助飞鱼雷计算模型如图1 所示,图中点A～I为设置的质量点。

图1 助飞鱼雷全雷简化模型Fig.1 Simplified model of a rocket-assisted torpedo

将简化后的模型导入Hypermesh 软件中进行网格划分,大部分采用6 面体单元,小部分采用4 面体单元,模型网格单元总计146 万余个,网格质量良好。网格模型如图2 所示。建立计算模型过程中,尽可能使主要连接结构与实际产品相同,如分离舱与鱼雷的止推块和止推槽模型、分离舱与设备舱的卡箍结构模型、楔环连接结构的阴阳头和楔环带模型等。上述3 种连接模型如图3所示。

图2 有限元网格模型Fig.2 Models of finite element mesh

图3 典型连接结构模型Fig.3 Typical connection structure models

为保证计算模型的准确性,计算模型的质量质心与实际模型相差不大,如表1 所示,其中质心位置为距雷头的轴向距离。

表1 计算模型物理参数Table 1 Physical parameters of calculating model

在Workbench 软件中进行助飞鱼雷的模态计算。计算模型的前处理过程中将大部分零部件间的接触设置为绑定状态,根据以往经验,考虑到鱼雷楔环连接结构的连接刚度较小,对全雷模态影响较大,其接触法向罚刚度系数取值0.00008,使楔环连接结构的连接刚度接近真实情况[9],保证弹性振动参数分析结果更加准确。因助飞鱼雷近似为回转体结构,认为其俯仰和横向振动特性相同,因而只分析计算助飞鱼雷的横向振动参数。

计算助飞火箭发动机满载(0 s)和空载(10 s)工况的模态,以模拟飞行过程中的2 个工作状态。

3 振动参数计算

3.1 模态振型

模态计算中,提取助飞鱼雷全雷前3 阶横向弯曲模态。全雷模态计算结果如表2 所示。从表中可以看出,各状态全雷同一阶模态振型相似,其中满载状态的全雷前3 阶模态振型如图4所示。

表2 全雷前3 阶模态振型Table 2 The first three order modal shapes of the whole torpedo

图4 满载状态下全雷前3 阶模态振型Fig.4 The first three order modal shapes of the whole torpedo at full load state

3.2 全雷振型函数

弹性体的横向振动可看作一系列分量的叠加,即

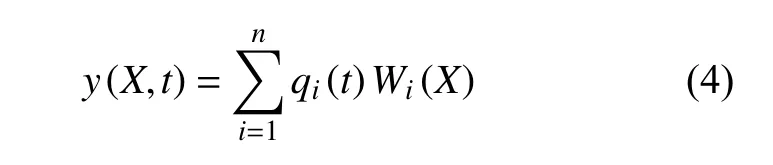
式中:y(X,t)为 振动位移;Wi(X)为弹性体第i阶固有振型函数;qi(t)为第i阶振型振动的广义坐标。

在进行弹性体振动特性参数计算时,通常取前3 阶模态进行分析计算。分析过程中将连续体离散处理,计算助飞鱼雷分析节点的振型向量。分析节点的数量(体现为间隔疏密)会影响斜率值的精确度,认为节点的数量应为能够反映关心模态振型的最小节点数的3 倍以上为佳,文中分析助飞鱼雷前3 节模态,至少需要5 个节点,那么计算振型斜率则至少需要15 个节点,因而文中分析模态振型斜率时在助飞火箭全雷二象限母线上取20 个等分节点,并在惯组安装处取1 个节点,21 个分析节点位置如表3 所示。

表3 分析节点位置Table 3 Position of analyzed nodes

通过后处理计算得到该21 个节点的振型向量,各计算状态分析节点的各阶振型如表4 所示。

表4 全雷分析节点模态振型Table 4 Modal shapes of torpedo’s analyzed nodes

将点A1 作为参考节点,将节点振型向量按参考点振型归一化处理[10]。全雷满载状态分析节点前3 阶模态振型如图5 所示(空载状态振型类似)。

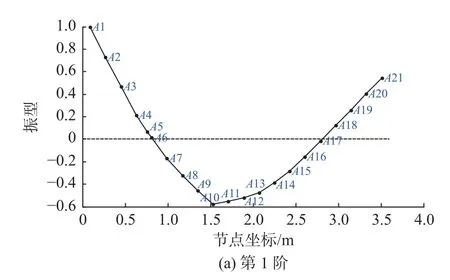
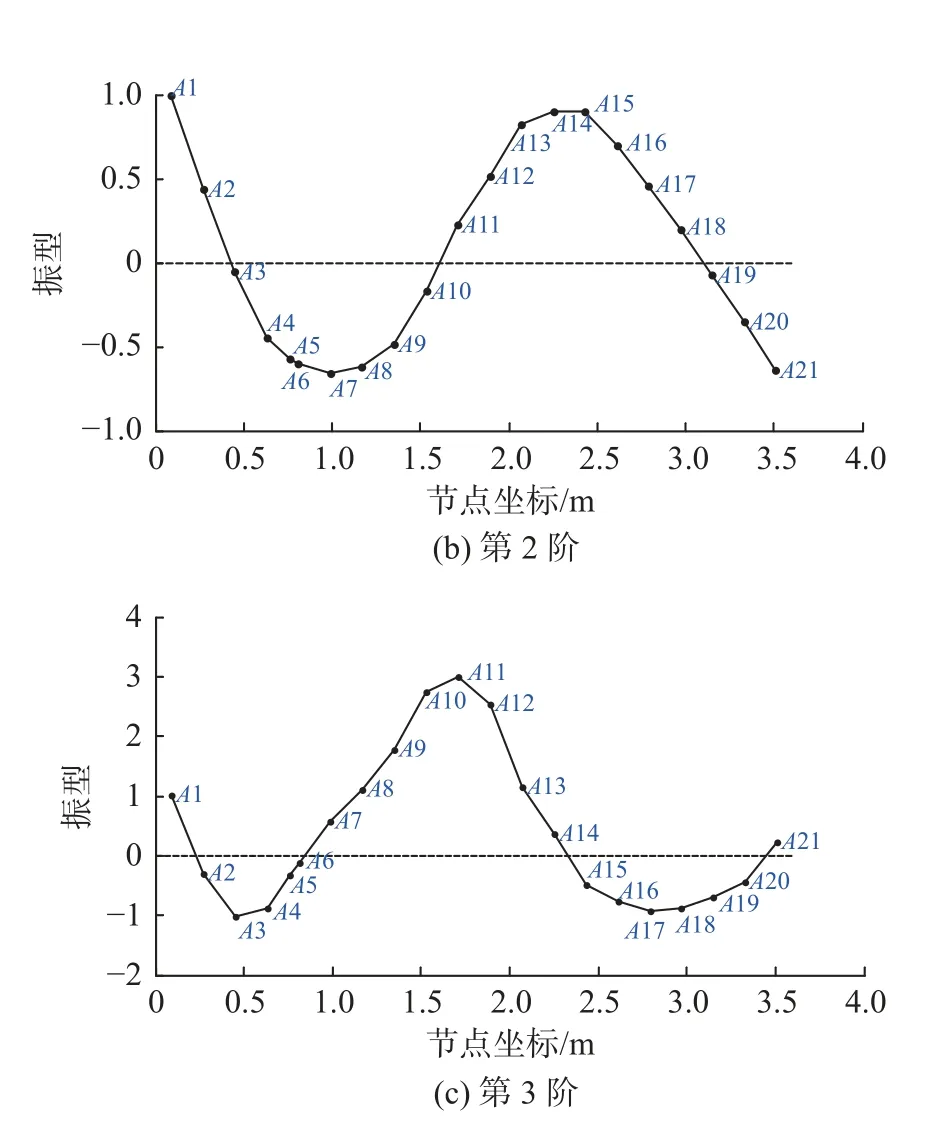
图5 满载状态下全雷节点前3 阶模态振型Fig.5 The first there order modal shapes of torpedo ’s Analyzed nodes at full load state

全雷节点振型向量对参考点归一化后(取雷头处点A1 为参考点),计算关心位置节点处的振型斜率。全雷状态惯组安装处振型斜率如表5 所示。

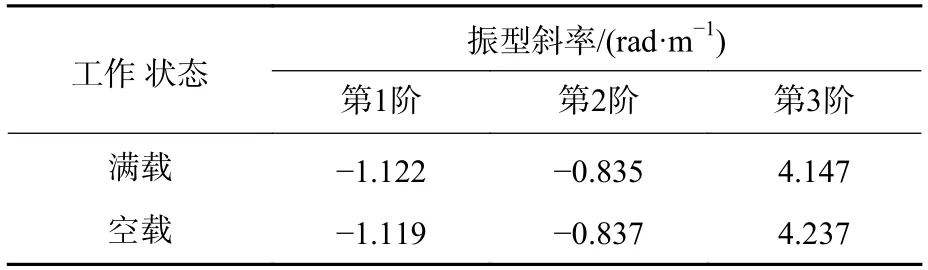
表5 惯组安装处舱壁振型斜率Table 5 Mode shape slope of inertial navigation’s position

4 结论

文中建立了助飞鱼雷动力学分析模型,并完成了助飞鱼雷模态振型斜率的仿真计算,得到以下结论:

1) 助飞鱼雷长细比较大,模态频率偏小,前2 阶模态频率均小于100 Hz,其整体刚度偏小,在气动力作用下引起的弹性振动不可忽略,姿控设计时需要考虑其影响;

2) 助飞鱼雷连接结构复杂,楔环连接结构、分离舱止推块结构以及分离舱卡箍结构影响全雷的连接刚度,进行详细三维建模可确保动力学分析模型的正确性;

3) 通过仿真方法进行振型斜率求解时,应按照参考点进行振型归一化处理后进行计算;

4) 参照图5(a)和图5(b)可以发现,前2 阶模态振型斜率较大的位置在A6、A17、A3、A19 位置,这几处位置不宜作为惯组等敏感元件的安装位置。

通过仿真计算方法得到的振型斜率其误差难以避免,为得到更加准确的振型斜率,仍需要根据试验值进行模型修正,共有2 种方法:一是根据模态频率试验值修正,再进一步求解振型斜率;二是直接根据振型斜率值进行计算模型修正。后期将进行产品模态试验或振型斜率测试试验,通过试验数据优化仿真计算方法。