基于GWO-LSSVM 的锂离子电池健康状态估算

李炬晨,胡欲立,高剑,曾立腾,郑乙,代文帅

(西北工业大学 航海学院,陕西 西安,710072)

0 引言

目前大多水下航行器的动力源多选用锂电池。为了不影响水下航行器的正常运行,在电池失效之前需要对其进行替换。而电池健康状态(state of health,SOH)是用来评价电池是否失效的主要指标。长期以来,SOH 的估算一直是国内外学者研究的重点。研究方法主要有特征法、模型法和数据驱动法[1]。特征法是通过测量电池老化过程内部参数的变化来估算电池的SOH 值[1-3],这种方法提取特征值的难度较大,仅适用于电池的生产设计过程。模型法一般从电池内部工作机理出发,建立能够反映电池性能退化规律的物理模型,从而预估电池的SOH[4-5],但由于电池内部的电化学反应过于复杂,内部衰退反应的参数同样难以测量,使得这种方法对电池SOH 的评估难度较大。数据驱动方法是目前应用最广泛的方法,如人工神经网络[6],支持向量机[7]等算法。该方法由于自身的简洁性,已逐渐成为锂电池SOH 研究领域的热点。其不需要关注电池的衰退机理,只需通过电池的相关测试数据建立与电池健康状态的响应关系,从而达到预估电池SOH 的目的。但存在需要大量的数据样本进行训练,且用于SOH 估算的效果不太理想等不足。针对此,文中基于数据驱动的方法建立了支持小样本数据且估算效果更好的算法模型。

支持向量机具有对样本数据依赖性低且稳定性好等优点,被广泛应用于性能退化数据分析的估算问题上,最小二乘支持向量机(least squares support vector machine,LSSVM)算法在支持向量机的基础上,变更了损失函数,提升了求解速度。同时,灰狼优化(grey wolf optimization,GWO)算法是一种新的智能群体算法,在求解精度和速度方面均有很好的表现,让其对LSSVM 算法进行优化将达到更好的效果。

综上所述,文中选用基于数据驱动的方法,建立了GWO-LSSVM 模型来估算电池SOH,并运用灰色关联度分析法来筛选数据驱动模型的输入特征参数。通过对18650 型钴酸锂电池做充放电循环实验,采用构建的算法对其进行SOH 估算,并将估算结果与基于网格搜索法(grind search,GS)的LSSVM 算法及基于粒子群优化算法(particle swarm optimization,PSO)寻优的LSSVM算法进行对比。

1 基于数据驱动的估算模型框架

对电池进行SOH 估算时,一般采用基于容量的SOH 定义[8],即

式中:C0为初始测得的放电容量;Ci为当前测得的放电容量。所以,电池当前的放电容量就可以用来表示电池的SOH。

在锂离子电池使用过程中去直接测量其当前放电容量是难以实现的,但是可以测量到其他特征参数,如:充放电时间、充放电电压等。通过对这些特征参数进行筛选,并将结果作为估算模型的输入特征参数就可以估算到电池的当前放电容量,其过程如图1 所示。

图1 基于数据驱动的估算模型框架Fig.1 Framework of data-driven estimating model

1.1 输入特征参数选取

水下航行器中的电池管理系统(battery management system,BMS)在电池充放电过程中会采集到大量的相关特征参数,筛选出与电池当前放电容量关联度高的特征参数是准确估算SOH 的基础。文中将通过灰色关联度分析法对这些参数进行筛选,选出与当前放电容量关联度最高的数据作为模型的输入样本。

灰色关联度分析是灰色数学中的一种分析方法,用来研究事物之间相互关联、相互作用的程度,确定影响事物的本质因素,使各种影响因素之间“灰色”的关系变得更加清晰[9]。

运用灰色关联度的具体步骤如下。

1) 确定母序列与子序列

母序列即为指标的参照对比项,子序列就是需要与母序列确定关联度大小的因素序列。

2) 归一化

用每个因素的值除以初值,从而使每个因素都能统一到近似的范围内,减少数据的绝对数值差异。

3) 计算灰色关联度系数

式中:x0(k)表 示当前放电容量;ρ表示控制灰色关联度系数的参数,一般取0.5;xi(k)表示第i个特征参数的第k个值。

4) 确定输入特征参数

计算出各个因素的关联度系数均值,并根据关联度系数均值和实际应用中数据获取的难易程度来选择输入特征参数。

1.2 GWO-LSSVM 模型

1.2.1 LSSVM 算法

在锂电池SOH 估算过程中,将筛选好的特征参数作为LSSVM 的输入数据集,当前放电容量作为其输出数据集,即可对SOH 进行准确的估算。LSSVM 是支持向量机的一种拓展方式,它将支持向量机的不等式约束改为等式约束,从而方便了拉格朗日乘子的求解,简化了计算过程,提高了计算精度。由文献[10]可知,LSSVM 模型的准确度主要依赖于核参数σ和正规化参数c的选择,所以对这2 个参数的寻优尤为重要。相比其他算法而言,GWO 算法有结构简单,精度高等优点,文中选择用该算法对σ和c进行寻优。

1.2.2 GWO 算法

GWO 算法是近几年提出的一种群智能优化算法[11],该算法受灰狼群体内领导层级和狩猎机制的启发而开发,将灰狼在头领的带领下进行捕食过程视为寻优计算,将狼群与猎物距离的不断更新视为最优解的迭代过程,对猎物好坏的选择过程判断即为避免算法陷入局部最优的过程,包围狩猎的过程即为求出最优解的过程。

1.2.3 GWO-LSSVM 估算模型

GWO-LSSVM 算法结合GWO 算法的高鲁棒性和LSSVM 算法的低复杂度,通过GWO 算法对LSSVM 算法中的超参数寻优,以达到更好的估算效果。图2 为GWO-LSSVM 估算模型流程图。

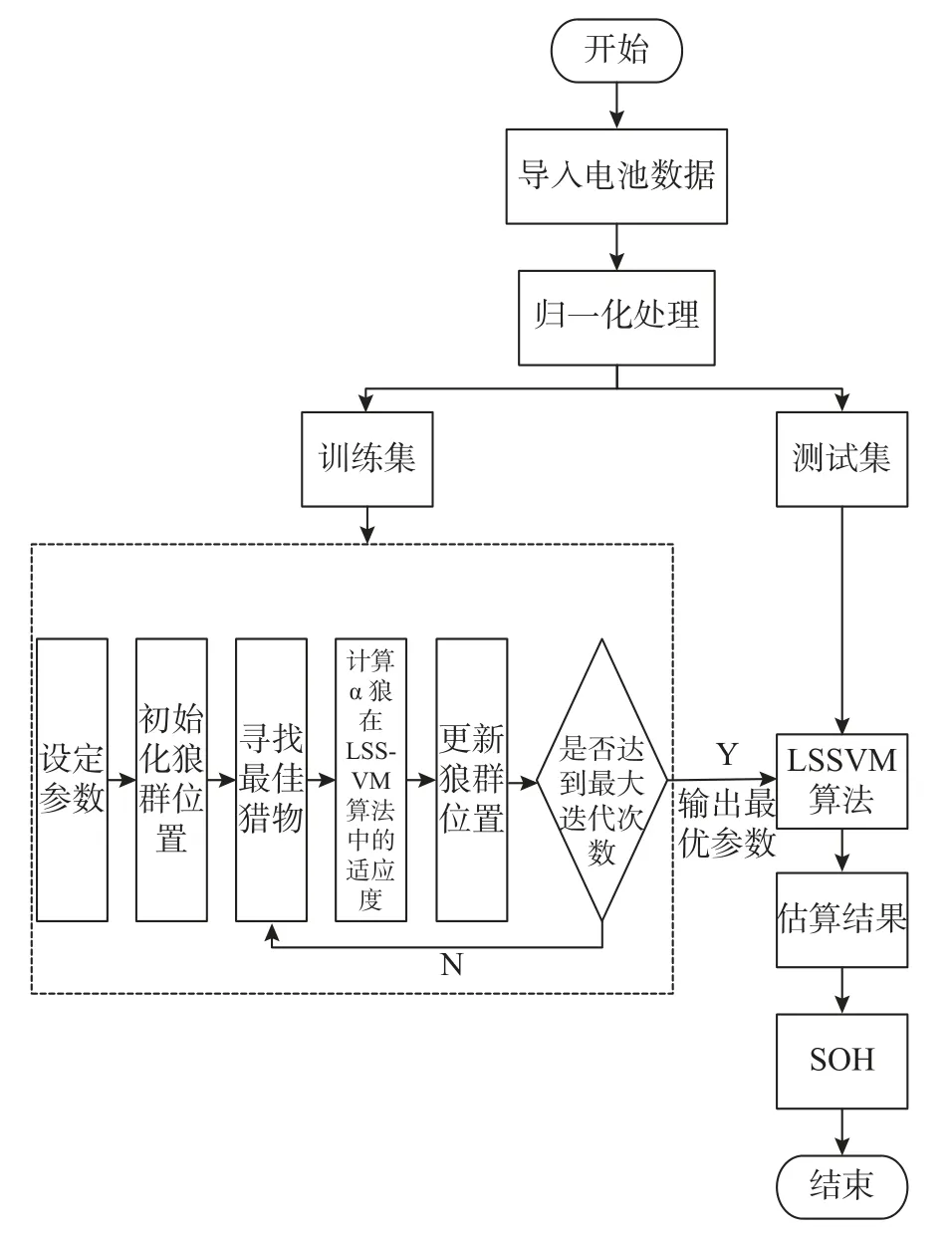
图2 GWO-LSSVM 估算模型流程图Fig.2 Flow chart of GWO-LSSVM estimating model

1) 导入数据:将灰色关联度分析法筛选出的电池特征参数作为模型的输入样本,电池放电容量作为模型的输出样本。

2) 对导入的数据做归一化处理,使其范围控制在(-1,1),则

式中:y为归一化后的数值;x为归一化前的数值;ymax=1;ymin=-1。

3) 确定训练集和测试集:分别选取电池数据中前30%,60%,90%的样本数据作为算法的训练集样本,电池数据中剩余部分作为算法的测试集样本,用来验证算法的精度。

4) 设置参数:将LSSVM 中参数σ和c的范围设置为(10-4,108),种群规模设置为20,种群维数设置为2,最大迭代次数设置为100。

5) 初始化狼群的位置,进行适应度计算并迭代寻优,根据其迭代次数是否达到最大来决定是否输出,达到即输出当前值,否则将进入下一次循环。

6) 将GWO 算法中寻找的最优解σ和c代入LSSVM 模型中,对电池的容量进行估算。

7) 得到估算结果后,根据式(1)将放电容量转化为SOH。

1.2.4 模型评价方法

确定估算模型之后,对其精度的检验必不可少。为了验证上文构建的GWO-LSSVM 估算模型是否适用于电池SOH 的模拟估算,选用平均绝对误差(mean absolute error,MAE)和均方根误差(root mean square error,RMSE)来检验算法的精度,计算公式分别为

式中:ya(i)为 实际值;yf(i)为估算值。

2 算例

2.1 充放电循环实验

如图3 所示,选用蓝电测试系统对2 种不同容量的18650 型钴酸锂电池进行充放电循环实验,为使实验效果尽可能地接近电池应用时的温度场景,没有控制温度这一变量,而是让电池在昼夜不同的温度下进行充放电实验。充放电循环制度流程如图4 所示。ICR18650 锂电池额定电压为3.60 V,内阻不高于30 mΩ,高度为65.0±0.15 mm,直径为18.30±0.10 mm,额定容量分别为2.55 Ah 和2.75 Ah,正极材料是LiCoO2,负极材料为石墨。

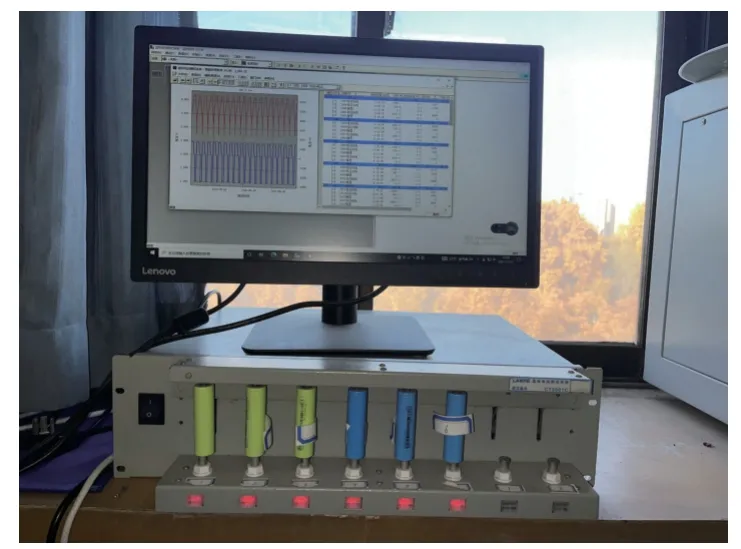
图3 充放电循环实验现场Fig.3 Charge/discharge cycle test site

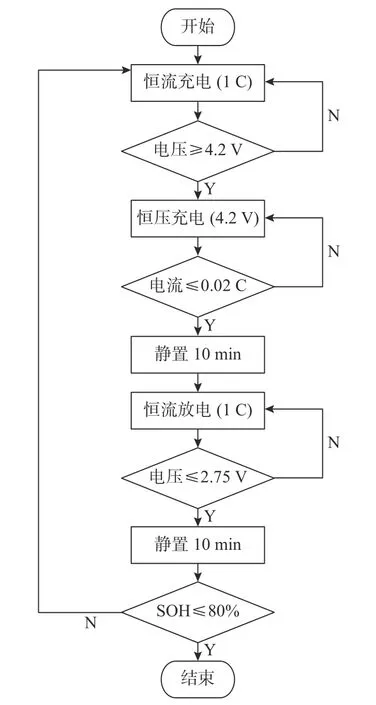
图4 电池充放电循环制度流程图Fig.4 Flow chart of battery charge/discharge cycle system

当锂离子电池的SOH 小于80%时即认为电池失效,通过整理电池放电容量数据,得到如图5所示的曲线,可以看出:随着实验循环次数的增加,电池的放电容量逐渐减小。

图5 电池放电容量衰减曲线Fig.5 Curves of battery discharge capacity attenuation

2.2 输入特征参数选取

在实际应用时,电池放电时的工况大多不同,而充电模式大体相同,所以选择将充电阶段的相关特征参数与放电容量进行灰色关联度分析。以第1 组电池为例,充电时间、恒流充电时间、恒压充电时间、等压段充电时间以及充电30 min 时的端电压都会随着循环次数的增加而发生相应变化,其变化曲线如图6 所示。

将图6 所示参数作为灰色关联度的子序列,放电容量作为母序列来进行灰色关联度分析,其结果如表1 所示。

表1 各个参数与容量的关联度均值Table 1 Mean value of relational grade between capacity and each factor

图6 特征参数变化曲线Fig.6 Curves of characteristic parameters

由表中数据可知,恒流充电时间与放电容量的关联度最高,故选择恒流充电时间作为输入特征参数。

2.3 估算结果

将恒流充电时间作为估算模型的输入特征参数,放电容量作为估算模型的输出特征参数,通过上文构建的GWO-LSSVM 算法对2 组电池进行估算,训练集样本比例分别为总样本数的30%,60%和90%。

1) 第1 组电池数据估算

经GWO 算法寻优得到的超参数如表2 所示。

表2 第1 组电池的超参数寻优结果Table 2 Optimization results of hyper-parameter of batteries from group 1

不同训练集样本的估算结果与真实值结果对比如图7 所示。不同训练集样本的估算结果精度对比如表3 所示。

从图7 和表3 可以看出,用第1 组电池数据进行估算,当训练样本为90%,60%和30%时,估算结果符合真实值的变化波动且误差偏差都较小。可初步认定GWO-LSSVM 算法在任何训练样本数据时,可以用于估算电池SOH,为进一步验证该算法是否使用于其他电池,对第2 组数据进行估算。

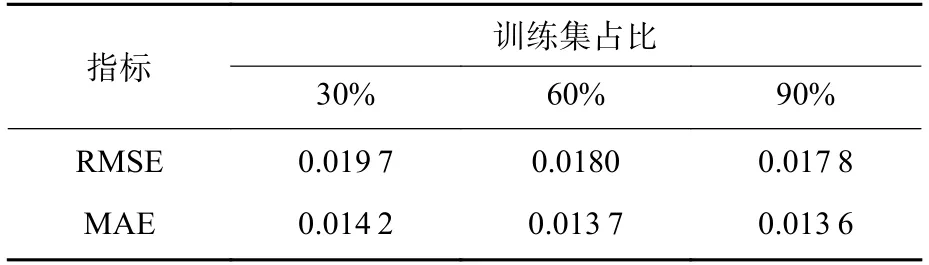
表3 第1 组电池的估算精度对比Table 3 Comparison of estimation accuracy for batteries from group 1

图7 第1 组电池的估算结果与真实值对比Fig.7 Comparison between estimated results and actual values of batteries from group 1

2) 第2 组电池数据估算

经GWO 算法估算得到的超参数如表4 所示。

表4 第2 组电池的超参数寻优结果Table 4 Optimization results of hyperparameter of batteries from group 2

不同训练集样本的估算结果与真实值对比图如图8 所示。

不同训练集样本估算结果精度对比见表5。

从图8 和表5 可以看出,用第2 组电池数据进行估算,当训练样本为60%和90%时,GWOLSSVM 算法的估算结果接近真实值,当训练样本为30%时,估算结果符合真实值的变化波动,估算误差比训练样本为60%和90%时的估算误差都大,但是其RMSE 和MAE 都在2%以内,可以认定GWO-LSSVM 算法适合用于估算电池SOH。

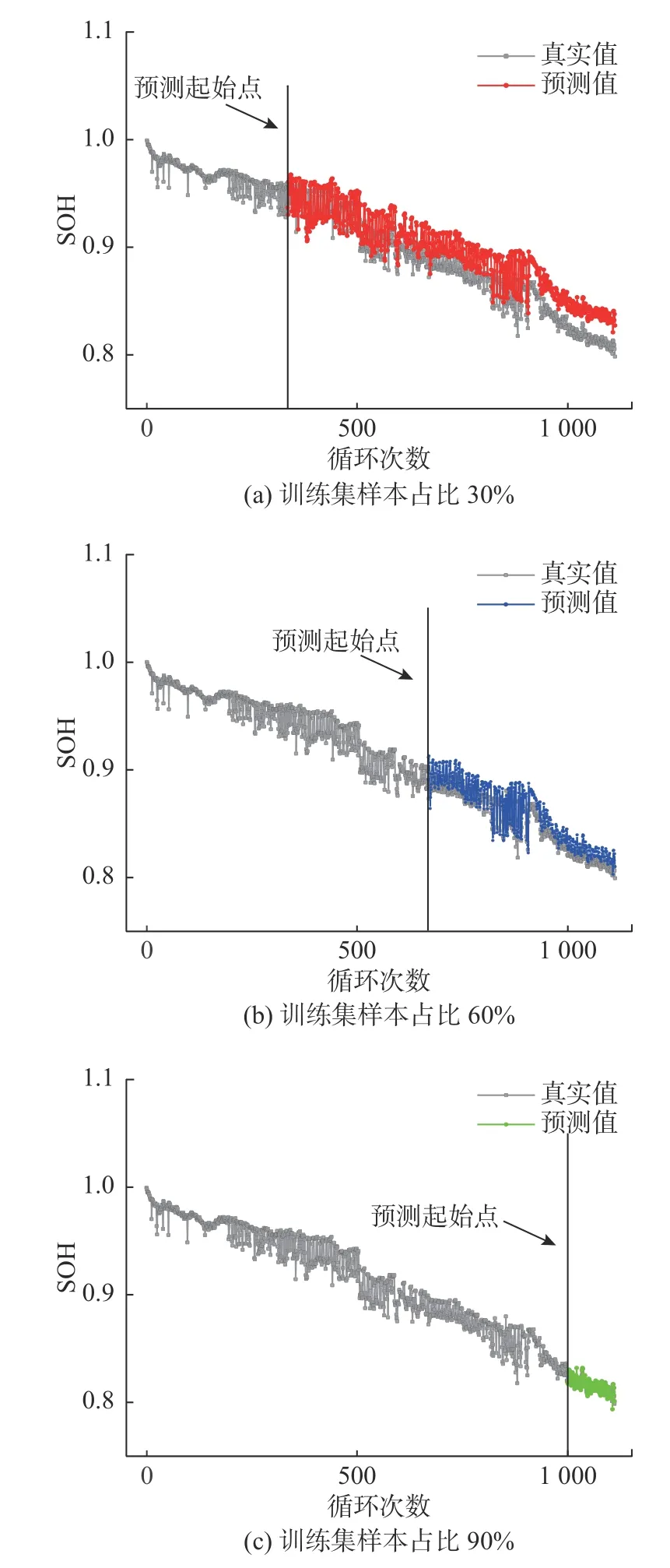
图8 第2 组电池的估算结果与真实值对比Fig.8 Comparison between estimated results and actual values of batteries from group 2

表5 第2 组电池的估算精度对比Table 5 Comparison of estimation accuracy for batteries from group 2

为验证GWO-LSSVM 算法的优劣性,选用GS-LSSVM 算法与PSO-LSSVM 算法分别对2 组电池进行估算,其对比结果如图9～图11 所示。GS 是LSSVM 超参数寻优中使用最广泛的一种方法,其首先确定参数的取值范围,然后以固定的步长沿不同方向划分网格,通过遍历网格来寻找最优解。PSO 算法是一种基于群体的智能优化算法,因其复杂度低、搜索能力强,且效率高而被广泛应用于参数寻优。

图9 不同算法在训练样本为30%时的估算结果对比Fig.9 Comparison of estimated results by different algorithms when the training sample proportion is 30%

从图9 可以看出:当训练样本为30%时,用GS-LSSVM 算法估算的效果都不佳,而PSO-LSSVM算法和GWO-LSSVM 算法的估算结果都与真实值有相同的变化波动。

从图10 可以看出:当训练样本为60%时,用GS-LSSVM 算法估算的结果在前期与真实值有相同的变化波动,但到了估算后期,估算值与真实值偏差较大,而PSO-LSSVM 算法和GWO-LSSVM算法的估算结果都与真实值有相同的变化波动且都接近真实值。

图10 不同算法在训练样本为60%时的估算结果对比Fig.10 Comparison of estimated results by different algorithms when the training sample proportion is 60%

从图11 的估算结果可以看出:当训练样本为90%时,用GS-LSSVM 算法估算的结果与真实值有相同的变化波动,但应用在第2 组电池时偏差太大,证明该算法不太稳定,普适性差。而PSOLSSVM 算法和GWO-LSSVM 算法的估算结果都与真实值有相同的变化波动且都很接近真实值。

图11 不同算法在训练样本为90%时的估算结果对比Fig.11 Comparison of estimated results of different algorithms when the training sample proportion is 90%

综上可以认定:GS-LSSVM 算法不适合用于电池SOH 估算,为进一步验证PSO-LSSVM 算法与GWO-LSSVM 算法估算效果的准确性,用RMSE和MAE 等指标对其进行对比。表6 列出了2 组电池及不同循环次数下估算结果精度。

分析表6 得出如下结论:

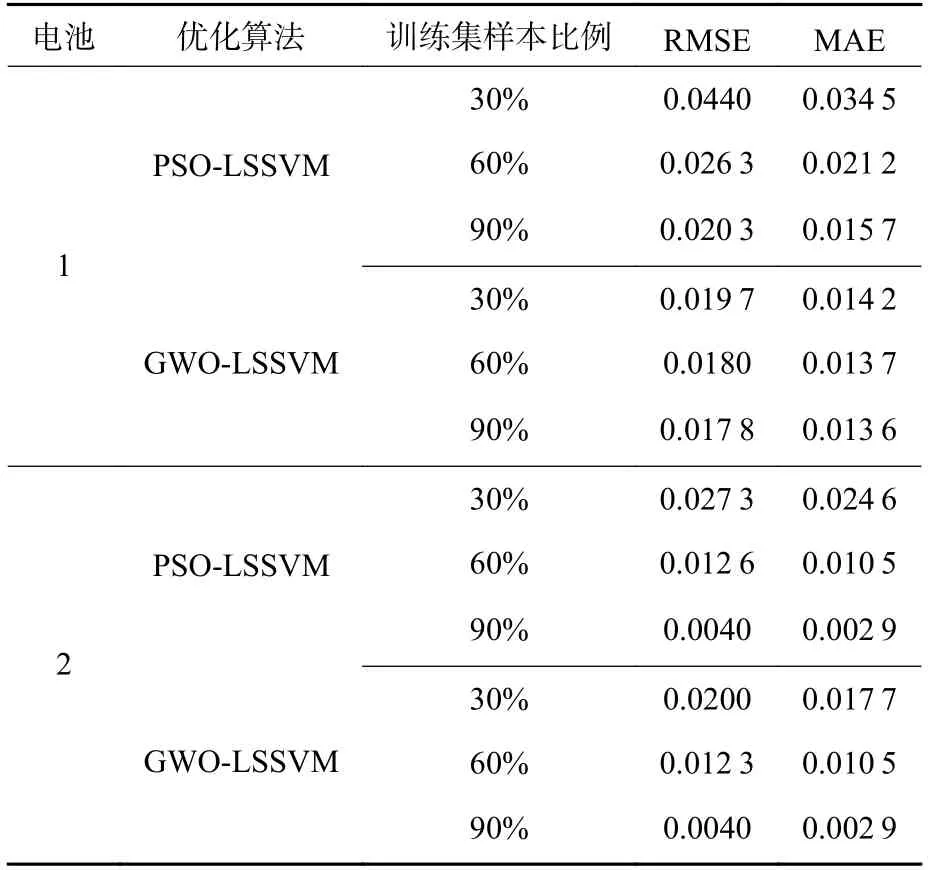
表6 2 组电池在不同算法不同训练集样本下的估算性能指标对比Table 6 Comparison of estimation performance specifications of different algorithms for the two groups of batteries with different proportions of training set samples

1) 将2 种算法应用到第1 组电池,当训练样本为30%时,GWO-LSSVM 算法的误差均小于PSOLSSVM 算法;当训练样本为60%时,GWO-LSSVM算法的均方根误差小于PSO-LSSVM 算法,平均绝对误差相同;当训练样本为90%时,GWO-LSSVM算法与PSO-LSSVM 的误差相同。

2) 将2 种算法应用到第2 组电池时,在训练样本不同的情况下,GWO-LSSVM 算法的误差均小于PSO-LSSVM 算法。

综上所述,可以认定PSO-LSSVM 算法在大样本情况下可以进行电池SOH 估计,但效果不如GWO-LSSVM 算法,而GWO-LSSVM 算法对于不同组电池及不同数量的训练集样本,都可以达到较高的精度,所以认为GWO-LSSVM 算法更适合用于电池SOH 估算。

3 结束语

电池SOH 的准确估算对电池使用的安全性尤为重要,目前应用于电池SOH 估算的算法需要用大量数据样本来进行估算且估算效果不佳,针对这一问题,文中通过灰色关联度分析算法对电池充放电循环实验数据进行分析筛选,选出恒流充电时间作为输入特征参数,同时结合GWO 算法和LSSVM 算法的优点构建出GWO-LSSVM 模型,在不同比例的训练集样本下对不同电池的SOH 进行估算,并将估算结果与GS-LSSVM 算法、PSOLSSVM 算法的估算结果进行对比。结果表明,GWO-LSSVM 算法应用于不同电池时的估算精度最高,且在小样本数据下有很好的估算效果。为提高电池SOH 评估的准确性,还需开展以下工作:1) 选用不同类型的电池进行研究;2) 设计更为复杂的实验工况进行实验验证;3) 将特征法或模型法与数据驱动的方法结合来对电池进行建模。