燃料电池客车系统建模与能量管理策略
袁 结,杨继斌,徐晓惠,陈 鑫,彭忆强,邓鹏毅
(西华大学汽车与交通学院,四川 成都 610039)
全球范围内环境污染和资源匮乏的问题制约着以化石燃料为能源的传统汽车的发展,因此燃料电池汽车作为新能源汽车的重要组成部分受到了更多的关注。燃料电池汽车凭借自身的高效、可靠和环境友好等优点,被寄希望于成为未来最理想的清洁能源汽车[1-2]。
能量管理是混合动力系统的核心,常见的能量管理策略总体可分为基于规则的控制和基于优化的控制两大类[3-6]。基于规则的能量管理策略包括开关控制策略、功率跟随控制策略和模糊控制策略[7]。文献[4]针对燃料电池混合动力汽车搭建了MATLAB/Simulink 与GT-Suite 联合仿真平台,以NEDC 工况作为测试工况,对不同的规则式能量管理策略进行研究,对比分析了不同能量管理规则对整车经济性的影响。文献[8]基于ADVISOR 搭建了燃料电池客车仿真模型,并制定模糊规则能量控制策略,结果表明整车经济性和燃料电池寿命得到提高。宋光辉等[9]基于Simulink与AVL CRUISE软件搭建增程式电动汽车联合仿真平台,研究了不同的功率跟随策略对整车经济性的影响。文献[10]搭建燃料电池电动汽车仿真平台,提出并构建一种用于扩展控制器的开关功率跟随控制策略,研究了跟随控制策略的模糊算法,仿真结果表明功率跟随模糊算法能提高燃料电池增程商用车动力系统的功率性能。因此,基于规则的能量管理策略具有技术难度低、计算量小和鲁棒性强等优点,被广泛地应用于混合动力汽车。基于优化的控制策略主要包括遗传算法[11]、动态规划算法[12]、模型预测控制[13]和等效消耗最小原则[14]。基于优化的能量管理策略计算量大、计算复杂且计算结果并不一定满足最优解,实车应用困难。
综上所述,本文针对燃料电池混合动力客车规则式能量管理策略开展研究,基于MATLAB/Simulink 搭建整车前向仿真模型,建立不同的控制规则,研究不同的规则式控制策略对燃料电池混合动力汽车整车经济性的影响。
1 燃料电池电动客车混合动力系统
燃料电池/动力电池双动力源混合动力客车系统结构图如图1 所示。在工作中燃料电池作为主要能源提供输出功率,动力电池作为辅助能源提供峰值功率和回收制动能量。关键零部件包括燃料电池、动力电池和电机等。

图1 混合动力系统结构图
整车模型是基于MATLAB/Simulink 搭建燃料电池电动客车前向仿真的数学模型,主要包括工况模型、驾驶员模型、能量管理策略、燃料电池系统模型、动力电池模型、传动系统模型和车辆纵向动力学模型。
2 整车系统建模
2.1 燃料电池系统模型
为了分析燃料电池在汽车行驶过程中的输出特性,需要搭建能真实反映燃料电池极化特性的数学模型。基于MATLAB/Simulink 仿真软件建立质子交换膜燃料电池(proton exchange membrane fuel cell,PEMFC)半经验动态数学模型[15]。模型的输入为负载电流Ifc,输出为燃料电池实际输出功率Pfc,具体PEMFC 系统基本参数见表1。在燃料电池的电化学反应过程中造成输出电压损耗的主要是欧姆过电压、活化过电压和浓度过电压,可以由式(1)表示。
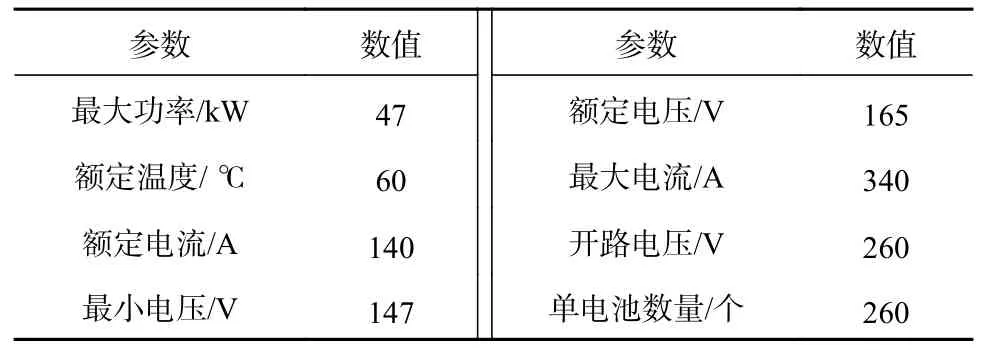
表1 PEMFC 基本参数
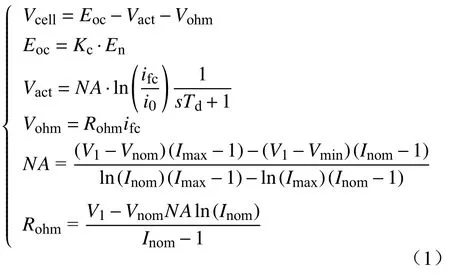
式中:En为能斯特电压,V;Vact为活化过电压,V;Vohm为欧姆过电压,V;Kc为电压常数;ifc为电堆电流,A;i0为交流电流,A;Rohm为电堆内阻,Ω;Vcell为单片燃料电池输出电压,V;s为传递函数符号;Td为电堆响应时间,s;N为电池数量;A为塔菲尔斜率;V1为电流为1 A 时的电压,V;Vnom为燃料电池额定电压,V;Vmin为燃料电池最小电压,V;Imax为燃料电池最大电流,A;Inom为燃料电池额定电流,A。燃料电池系统输出电压与输出功率由式(2)—(3)表示:

式(2)中,n为单电池数量。
PEMFC 系统模型仿真结果与实验数据对比特性曲线如图2 所示,图中蓝色散点与红色散点分别表示PEMFC 系统输出电压和输出功率的试验数据,蓝色曲线和红色曲线分别表示PEMFC 系统输出电压和功率的仿真曲线。从图2 可以看出,搭建的系统模型能较好地反应燃料电池实际的电压与功率输出,证明了PEMFC 系统模型的可靠性。
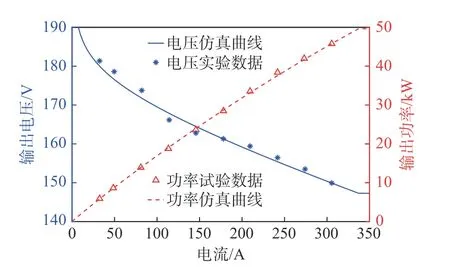
图2 燃料电池系统极化特性曲线
2.2 动力电池模型
当车辆行驶过程中,遇到爬坡或加速时需要动力源提供较高的功率,此时燃料电池不足以单独提供功率,需要辅助能源与燃料电池一起提供功率输出。当车辆需要制动时,为了实现能源的最大利用,需要辅助能源回收制动能量,所以本文选择动力电池作为辅助能源提供峰值功率和回收制动能量。
本文根据参考文献[16]中应用的模型,通过电池放电曲线的3 个节点计算出电池所需的模型参数。放电过程中电池的端电压Vbatt可通过式(4)给出,充电过程中电池的端电压Vbatt可通过式(5)给出。


公式(4)—(5)中的3 个参数E0、K和A0可通过放电曲线3 个节点计算,如图3 所示。从图中取出3 个节点分别为(0,Vfuel)、(Qexp,Vexp)和(Qnom,Vnom),3 个点对应的坐标为(0,3.5)、(5.76,3.24)和(228,3.01)。将坐标代入公式(4)可计算出E0、K和A0的值,即可得到动力电池充放电曲线参数。

图3 动力电池放电曲线
采用安时积分法计算电池SOC。

式中,Q0表示电池初始容量。电池模型仿真得到放电曲线如图4 所示。

图4 动力电池放电容量仿真结果
2.3 电机模型
电机模型采用的是理论模型和电机效率MAP 图的静态模型,用式(7)—(11)描述。

式(7)—(11)中:Tmax_dis表示电机处于驱动状态下的最大转矩,N·m;Tmax_char表示电机处于回收制动状态下的最大转矩,N·m;ωm表示电机转速,根据车速估算得到,r/min;Treq表示电机需求转矩,N·m;j表示传动系统传动比,取j=6.14;va表示当前时刻车速,km/h;rm表示车轮半径,取rm=0.435;P表示混合动力源模型的输出功率,kW。电机效率MAP 图如图5 所示。

图5 电机效率MAP 图
2.4 车辆纵向动力学模型
本文的研究对象为成都客车股份有限公司开发的某款燃料电池客车,具体整车参数如表2 所示。

表2 整车参数
模型中仅考虑车辆行驶过程中的空气阻力、滚动阻力、坡道阻力和加速阻力。车辆的纵向驱动力平衡方程式如下:
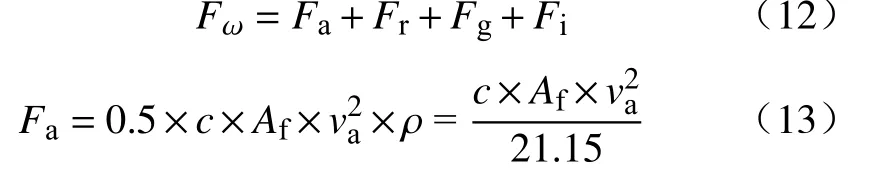
式(12)—(13)中:Fa为空气阻力,N;Fr为滚动阻力,N;Fg为坡道阻力,N;Fi为加速阻力,N;c为空气阻力系数;Af为迎风面积,m2;ρ为空气密度,kg/m3;v为当前车速,m/s。整理可得
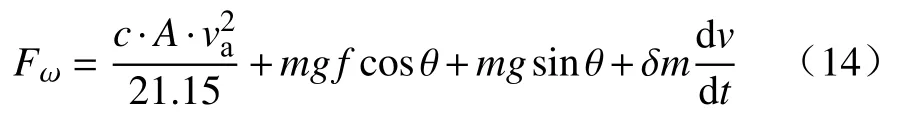
式中:m为 整车整备质量,kg;f为滚动阻力系数;θ为道路坡度角,rad;δ为车辆旋转质量换算系数;g为重力加速度,m/s2。
2.5 驾驶员模型
驾驶员模型采用最基本的PID 驾驶员模型,通过将需求速度与车辆实时速度之间的差值模拟为驾驶员踩踏加速踏板和制动踏板的动作,从而调节车辆速度,可用式(15)—(16)描述。
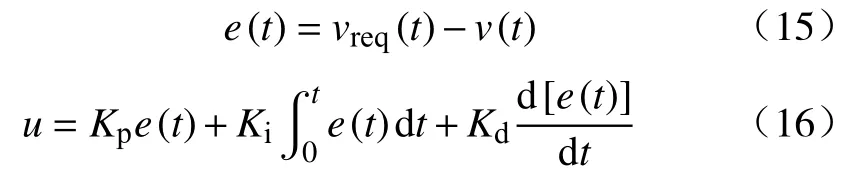
式(15)—(16)中:e(t)表示t时刻车辆需求速度与实际速度之间的差值;vreq(t)表示需求车速;v(t)表示实际车速;u∈[-1,1],当u<0时表示车辆处于制动状态,当u>0时表示车辆处于加速状态;Kp、Ki、Kd分别表示PID 环节的比例、积分和微分的比例系数。
2.6 能量管理策略
能量管理策略(energy management strategy,EMS)控制着燃料电池和动力电池的功率输出,将车辆行驶的需求功率更合理地分配给混合动力源,直接影响着整车的经济性。本文提出4 种规则式能量管理策略,基于Simulink/Stateflow 对能量控制策略进行建模,通过仿真结果对比分析不同规则对经济性的影响。在规则制定时尽量保证动力电池SOC 处于0.2~0.8 区间[8],其中规则一和规则二为功率跟随控制策略,规则三和规则四为开关控制策略。
功率跟随控制策略是使燃料电池作为主要能源输出,动力电池作为辅助能源,根据当前驾驶员需求功率、动力电池荷电状态、发动机的转速状态和当前车速选择合适的工作模式。
开关控制策略是根据实车运行数据分析总结得到。当动力电池SOC 值大于80%时,动力电池作为主要能源输出,当动力电池SOC 值小于80%时,燃料电池作为主要能源输出,根据当前驾驶员需求功率、动力电池荷电状态、发动机的转速状态和当前车速选择合适的工作模式。
规则一:优先燃料电池功率输出,动力电池作为辅助能源提供峰值功率和回收再生制动能量,车辆运行期间燃料电池不给动力电池充电。
规则二:优先燃料电池功率输出,动力电池作为辅助能源和回收再生制动能量,当动力电池SOC<80%时,燃料电池可以给动力电池充电。
规则三:当电池SOC≥80%时,优先电池功率输出,否则燃料电池优先输出,期间燃料电池不给动力电池充电,当电池SOC≤95%时,动力电池可回收再生制动能量。
规则四:当电池SOC≥80%时,优先电池功率输出,否则燃料电池优先输出,燃料电池可给动力电池充电,当电池SOC≤95%时,动力电池可回收再生制动能量。
其中规则一的控制逻辑描述如图6 所示。
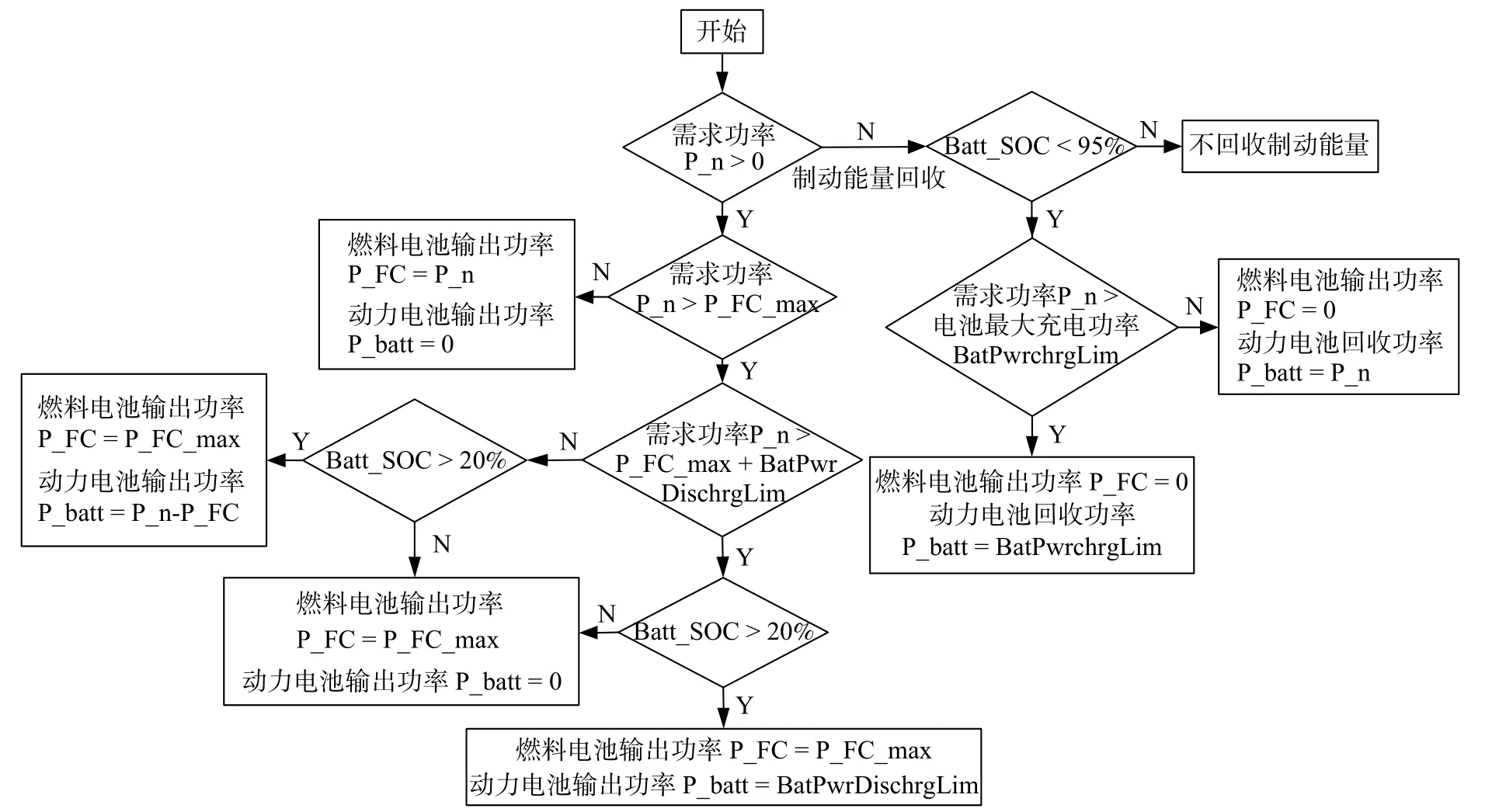
图6 规则一控制逻辑
3 模型验证与结果分析
在MATLAB/Simulink 平台上搭建燃料电池电动客车系统模型,如图7 所示,通过制定的4 种规则式能量管理策略验证搭建车辆模型的有效性。使用中国普通客车行驶工况(CHTC-C)进行仿真,仿真结果如图8 所示。由图可以看出4 种策略仿真得到的速度曲线完全重合,所以4 种策略均能满足工况运行需求。

图7 燃料电池电动客车系统结构图
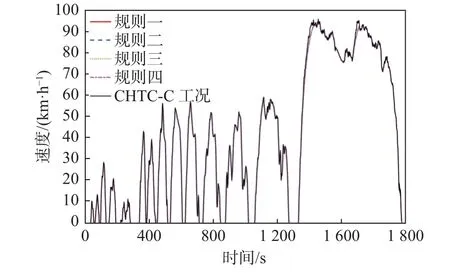
图8 车速仿真曲线
通过仿真可以得到4 种规则对应的仿真运行对比数据如表3 所示,包括运行里程、最高速度、平均速度、最大加速度和最大减速度。
从图8 和表3 中的运行数据可以看出,提出的4 种规则均能满足CHTC-C 工况的速度需求,能合理地分配车辆行驶需求功率,表明制定的规则有效。
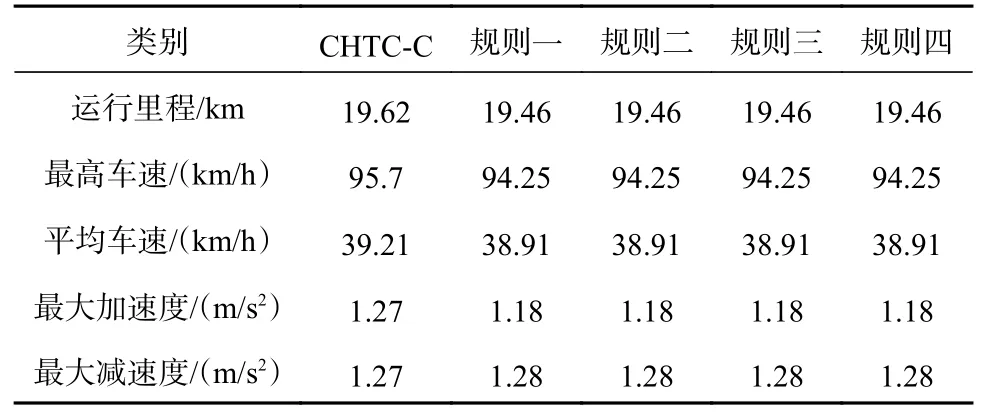
表3 运行对比数据
为了能更准确地得到4 种规则对经济性的影响,本文将5 个连续CHTC-C 工况组合成组合工况,分别把4 种规则代入整车模型进行经济性验证,得到氢气消耗量对比曲线如图9 所示,动力电池SOC 变化曲线如图10 所示。
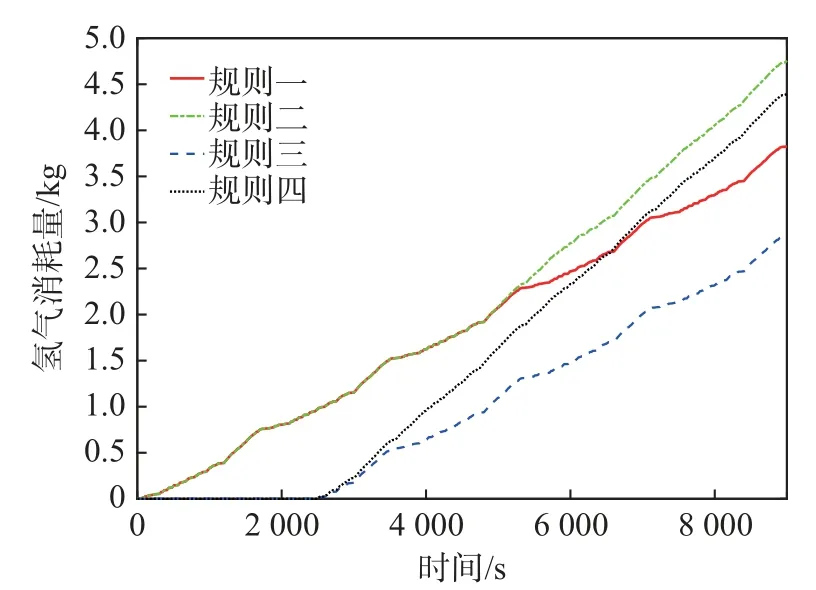
图9 不同规则下氢气消耗量对比
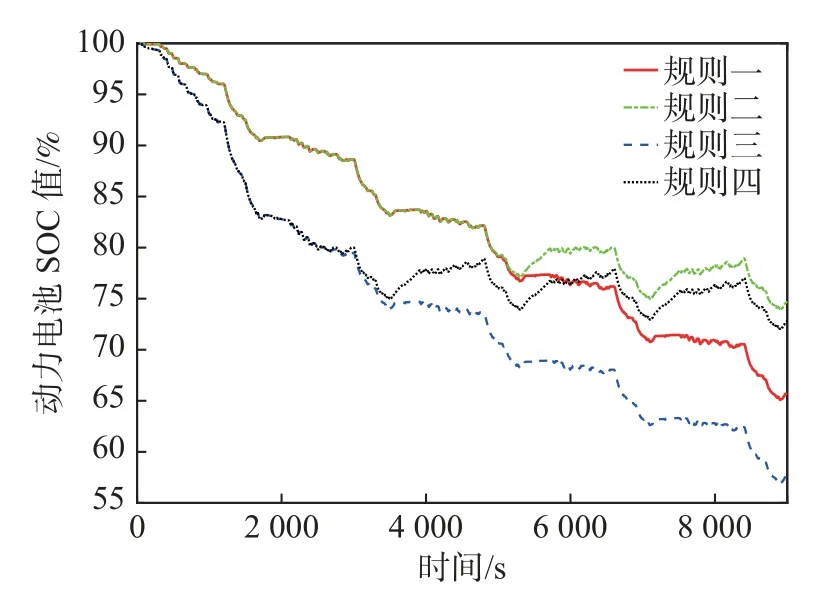
图10 不同规则下动力电池SOC 变化曲线
从图10 可以看出:在对5 个CHTC-C 的组合工况进行仿真时,基于功率跟随式控制策略的规则一和规则二在动力电池SOC≥80%时同步下降;当动力电池SOC<80%时,规则二可在燃料电池输出功率大于需求功率时给动力电池充电;基于开关控制策略的规则三和规则四中,动力电池为主要能源输出,两种策略运行结果显示在动力电池SOC≥80%时,SOC 值同步下降,在动力电池SOC<80%时,规则四可在燃料电池输出功率大于需求功率时给动力电池充电。
为了能更直观地对比经济性验证结果,使用公式(17)—(18)将电池电量消耗量折算为燃料电池氢气消耗量。
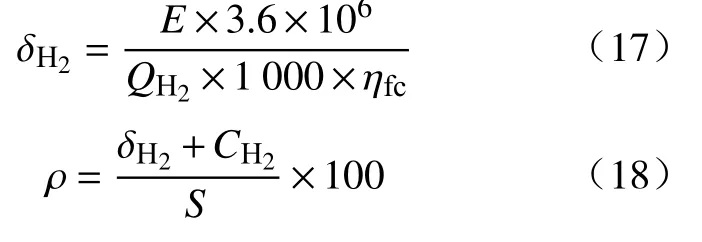
式(17)—(18)中:E为电池容量,kW·h;为氢气低热值,取120×103J/g;ηfc为燃料电池平均效率,取ηfc=0.45;为电池等效氢气量,kg;表示燃料电池氢气消耗量,kg;S表示行驶里程,km。将仿真数据代入公式(18)计算得出4 种规则的每百公里等效氢气消耗量如表4 所示,其中每百公里等效氢气消耗量最低的是规则三,为6.447 kg。

表4 4 种规则的每百公里等效氢耗
4 结论
本文以燃料电池电动客车为研究对象,基于MATLAB/Simulink 平台搭建整车前向仿真模型,以CHTC-C 工况作为研究工况,对搭建的模型进行经济性仿真测试,主要结论如下。
1)基于MATLAB/Simulink 平台搭建整车前向数学仿真模型,通过各系统仿真结果表明所搭建数学模型的有效性。
2)基于Stateflow 建立4 种规则式能量管理策略,通过对比车速仿真曲线、运行里程、最高车速、平均车速、最大加速度和最小加速度,结果表明所搭建策略在满足CHTC-C 工况运行要求的基础上,能有效地判断当前车辆需求功率,并合理分配给燃料电池和动力电池。
3)使用5 个连续中国普通客车行驶工况(CHTC-C)验证能量管理策略对经济性的影响,将动力电池的电量消耗折算为氢气消耗,得到每百公里等效氢气消耗量,结果表明规则三每百公里等效氢耗最低,为6.447 kg。

