基于DE-PSO 算法的反时限过流保护定值整定优化
高 佳,董上义,彭章刚
(国网四川省电力公司内江供电公司,四川 内江 641000)
保护装置的定值优化是微机继电保护领域的一个重要研究课题。对定值进行优化计算是高效发挥保护装置性能的关键。反时限过流保护的动作时间随着短路电流的增大而减少,具有一定的自适应性,因而受到用户青睐,并得到大量应用。为使反时限过流保护在满足灵敏性和选择性的前提下,达到继电器预先设定的最佳动作时间,制定有效的定值优化方案变得尤为重要[1]。目前针对反时限过流保护定值优化的研究主要在定值整定优化模型的建立、实际工况下继电保护装置的约束条件等方面[2]。保护定值优化模型是一个带有多个变量和复杂约束的非线性优化问题[3]。常规的数学方法难以快速求得这类非线性优化问题的最优解。群智能算法以其结构简单、求解速度快的特点,成为解决最优化问题的有效工具。狼群算法、蜂群算法、鱼群算法等一系列拟生算法相继被提出来,并用于处理工程中遇到的实际问题[4]。这些群智能算法用于处理问题的类型不同,收获的效果优劣不一。因此,找到适合的优化算法用于处理定值整定优化是本文研究的重点。文献[5]针对配网系统中保护间的协调问题,建立了反时限过流保护定值优化的非线性模型,提出一种改进的SOS 算法用于求解优化模型,算例结果表明,改进算法对提高保护的速动性效果良好。文献[6]分析了反时限过流保护与定时限保护之间的定值整定配合方式,采用K-PSO 算法用于反时限过流保护整定计算与定值优化。文献[7]为了提高系统的安全运行,以CCT 权重的方法修正优化目标函数,利用粒子群算法优化整定模型,算例结果验证了经过修正后的整定模型能缩短严重故障时的动作时间。文献[8]建立的反时限过电流保护定值优化模型考虑了新能源发电接入对目标函数的影响,在建立约束条件时考虑了保护装置的固有特性,简化了保护之间的配合关系,仿真结果验证了模型的适用性。文献[9]为了处理发生大短路电流造成模型计算无解的情况,将配网主保护与后备保护的总动作时间最小作为优化目标,计及装置实际工作下的约束条件,建立了配网反时限过电流保护定值优化模型,采用权重系数改善算法性能,仿真算例结果验证了策略的正确性。
本文以反时限过流保护动作时间最短为优化目标,结合继电器实际工况需要满足的灵敏性、选择性以及自身的性能要求等约束,建立了反时限过电流保护定值整定优化模型;针对粒子群算法容易陷入局部最优解的缺陷,提出一种基于PSO 和DE 的混合算法作为优化模型的求解方法;将混合算法与相关算法分别用于反时限过流保护定值整定,以验证本文的差分粒子群混合算法(DEPOS 算法)求解反时限过流保护定值整定问题具有更优的性能。
1 反时限过流保护定值整定优化模型
1.1 目标函数
反时限过电流保护的动作时间随着故障电流的升高而降低,可以依据流过线路的故障电流调整动作时间,具有一定的自适应性[10]。合理的整定反时限过电流保护动作时间,能够提高继电保护的速动性。反时限过电流保护的优化整定,就是要求在满足各项约束条件的前提下,实现各个继电器动作时间值的总体最小。其目标函数可以表示为

式中:Tl·i表示反时限继电器i在线路l处的动作时间;N为线路的总条数;K为继电器的总个数。
本文的优化模型采用常规反时限特性,以继电器整定系数TDS 和启动电流Iop为优化变量,减少继电器总的动作时间值T。
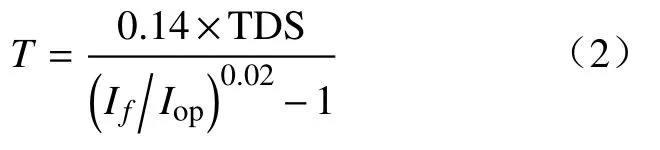
式中:TDS 为继电器的整定系数;If为流过继电器的短路电流。
将式(2)代入式(1),可以得到反时限过流保护定值整定优化的目标函数,为

1.2 约束条件
1)为保证继电器能够躲过最大负荷电流,同时在最小故障电流时准确动作,继电器应具有一定的灵敏度,即

式中:Iop为继电器的启动电流;Il·max为线路最大负荷电流;Il·min为线路最小故障电流。
2)为了保证主保护和后备保护之间的选择性要求,需要设计主、后备间的时间级差,即

式中:Tj·k为继电器j作为后备保护在故障点k处的动作时间;Ti·k为继电器i作为主保护在故障点k处的动作时间。
3)继电器时间整定系数的范围为

式中:TDSi·min、TDSi·max分别为最小时间整定系数和最大时间整定系数。
4)继电器动作时间的范围为
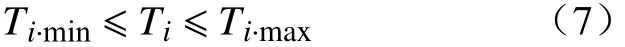
式中:Ti·min、Ii·max分别为最小动作时间和最大动作时间。
2 差分粒子群混合算法
2.1 PSO 算法
粒子群优化(particle swarm optimization,PSO)算法是受到鸟类群体行为的启发而被提出的[11-12]。空间的可能解被描述为一个无质量、无体积的粒子,每个粒子在解空间不停的搜寻,记录自身在搜索过程中经历的最佳位置,同时粒子在可行域的位置和速度不仅受到自身经验的影响还受到群体最优位置的引导,粒子通过种群间个体的合作与竞争来求解优化问题。假设在一个D维的目标搜索区域内,群体中的粒子个数为N,第i个粒子的向量可以表示为Xi=(xi1,xi2,···,xiD),i=1,2,···,N。群体中粒子的速度可以表示为Vi=(vi1,vi2,···,viD),i=1,2,···,N。第i个粒子的最优位置称为个体最优位置Pbest=(pi1,pi2,···,piD),i=1,2,···,N。群体搜索到的最优位置记为全局最优位置Pg。其速度和位置更新公式可以表示为:

式中:vij(t+1)为下一次迭代的粒子速度;xij(t+1)为下一次迭代的粒子位置;w为惯性系数,表示对上一次飞行速度的继承程度;c1和c2为学习因子。
2.2 DE 算法
差分进化算法(differential evolution algorithm,DE)是一种高效的全局优化算法[13],包含较少的控制参数,结构简单、收敛速度快,对于大多数非线性、多目标优化问题,具有较好的可靠性和适用性。
随机生成符合均匀概率分布的NP 个参数向量,作为每一代的初始种群,即

式中:NP 为种群数量;G为进化代数。
1)变异操作。随机在每一代初始种群中选择3 个互不相同的个体,变异向量由式(11)产生。

式中:r1、r2、r3互不相同,F为变异算子,其值在0~ 2 间。
2)交叉操作。为了丰富种群的多样性,将目标向量与变异向量进行二项式交叉,生成交叉种群。
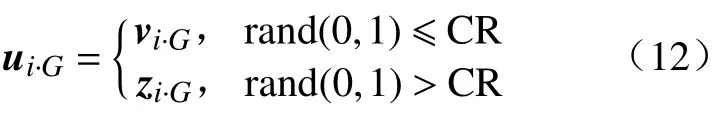
式中:rand(0,1)为随机产生的0~ 1 的数;交叉概率CR 为[0,1] 区间的一个常数。
3)选择操作。将试验向量ui·G与目标向量zi·G进行一对一的选择,具有更好适应度值的向量保留到下一代。选择操作表达式为
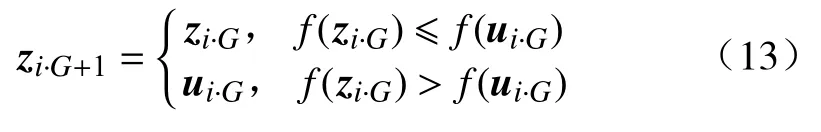
式中f(·)为最优适应度数。
2.3 基于PSO 和DE 的混合算法
随着迭代进行,PSO 算法的结构缺点逐渐显露出来,由于前期飞行速度过快,粒子快速地向局部最优解靠拢,造成粒子在后期迭代中种群多样性逐渐丧失。DE 算法的变异和交叉步骤增强了种群的差异性。但变异和交叉操作的实施动力来源于个体向量间的差异化,在迭代后期,个体向量间差异信息逐渐消失,造成后期搜索过程中收敛速度放慢。将PSO 和DE 相混合,能够增强种群多样性,提高个体跳出局部最优解的能力。2 种算法复杂程度低、编程容易实现,混合处理不会增加迭代过程中的计算量。
在混合算法的初始结构中将DE 和PSO 分为2 个并行迭代的子种群,每迭代一次,找出粒子种群的最优适应度值gbest和差分子种群的最优适应度值xbest。粒子群算法速度公式的第3 部分表示粒子向全局种群最优个体靠近的能力。为了增强粒子向2 个子种群中最优个体学习的能力,每迭代一次,对2 个子种群的最优适应度值进行判断,如果差分种群中的最优适应度值小于粒子种群最优适应度值,则将速度更新式(8)的第3 部分的最优位置Pg替换为差分种群中的位置最优个体Xg,用于指导粒子向全局种群的最优个体靠近。混合算法的流程如图1 所示,混合算法中粒子的速度更新公式为:
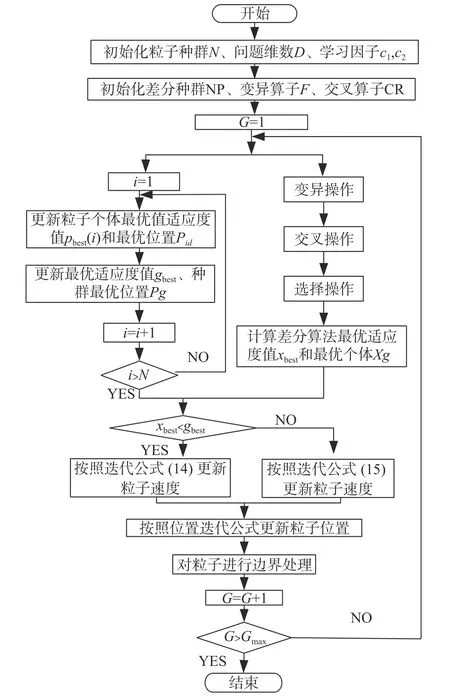
图1 粒子群差分进化混合算法流程
如果xbest<gbest,则
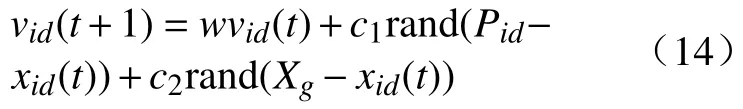
如果xbest≥gbest,则

2.4 基准测试函数
在智能算法,如神经网络算法、免疫算法、SA 算法等中,通常采用具有欺骗性的基准函数来测试算法的性能。常用的基准函数的表达式如表1所示。本文采用表1 中4 个基准测试函数对A-PSO算法(自适应粒子群算法)、A-DE 算法(自适应差分简化算法)、SA 算法(模拟退火算法)、DE-PSO算法(本文的粒子群差分混合算法)进行测试。测试中分别执行20 次后取均值,迭代搜索到的全局最优值如表2 所示。图2 示出基准测试函数的收敛特性情况。为了更好地观察迭代过程,将适应度值采用对数处理。由表2、图2 可知,采用DEPSO 优化的基准测试函数具有更佳的性能。

图2 基准测试函数的收敛曲线

表1 测试函数
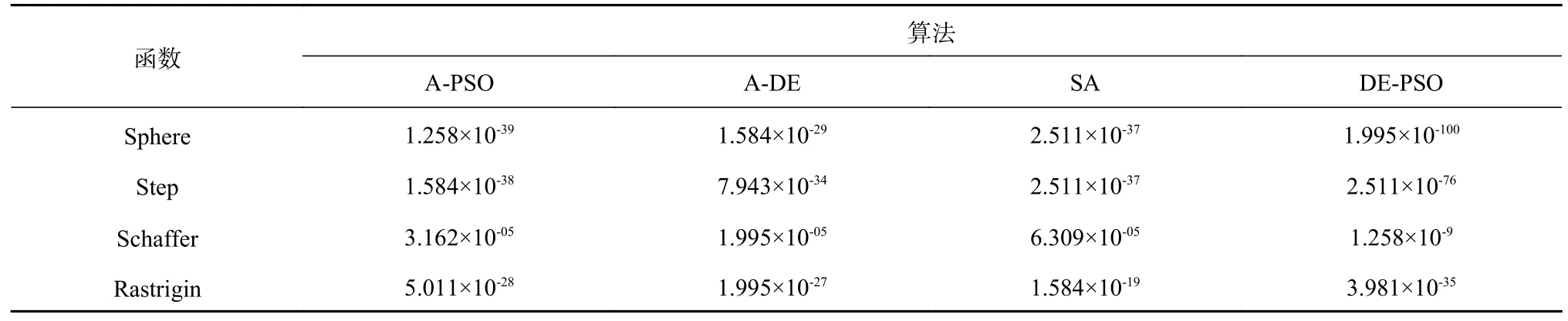
表2 基准测试函数的迭代结果
3 算例分析
为了验证本文的DE-PSO 算法对反时限过流保护定值整定优化的适用性及可行性,构建了如图3 所示的简易电网系统,包含3 个交流电源、9 条线路、3 条重要负载。系统配置了反时限继电器R1—R21。电网系统参数如表3 所示。

表3 电网系统参数

图3 简易的电网系统
将反时限继电器的整定系数TDS、启动电流Iop作为决策变量,网络中故障总体持续时间作为优化目标,建立反时限过流保护定值整定优化模型,分别采用DE-PSO 算法、A-PSO 算法、A-DE算法进行求解,比较3 种算法的寻优结果,以检验DE-PSO 算法的适用性和可靠性。A-PSO 算法、ADE 算法和DE-PSO 算法的参数设置表4 所示。

表4 相关算法的参数设置
将故障设置在线路BC 中间位置,故障类型为最严重的三相短路故障,采用Simulink 搭建仿真模型,计算出各线路的故障电流,如表5 所示。

表5 线路BC 三相短路时流过各线路的短路电流
以上述网络结构为研究对象,分别设置3 组实验:第1 组采用A-PSO 算法求解反时限过电流保护定值整定优化模型;第2 组采用A-DE 算法求解模型;第3 组采用DE-PSO 算法求解模型。通过比较3 种算法对微网经济运行优化结果,检验DEPSO 算法是否具有更佳的寻优结果。
1)第1 组仿真结果。采用A-PSO 算法作为求解算法,对整定系数TDS、继电器的启动电流Iop以及总动作整定时间的求解结果如表6 所示。

表6 A-PSO 算法的求解结果
2)第2 组仿真结果。采用A-DE 算法作为求解算法,对整定系数TDS、继电器的启动电流Iop以及总动作时间的求解结果如表7 所示。

表7 A-DE 算法的求解结果
3)第3 组仿真结果。采用DE-PSO 算法作为求解算法,对整定系数TDS、继电器的启动电流Iop以及总动作时间的求解结果如表8 所示。
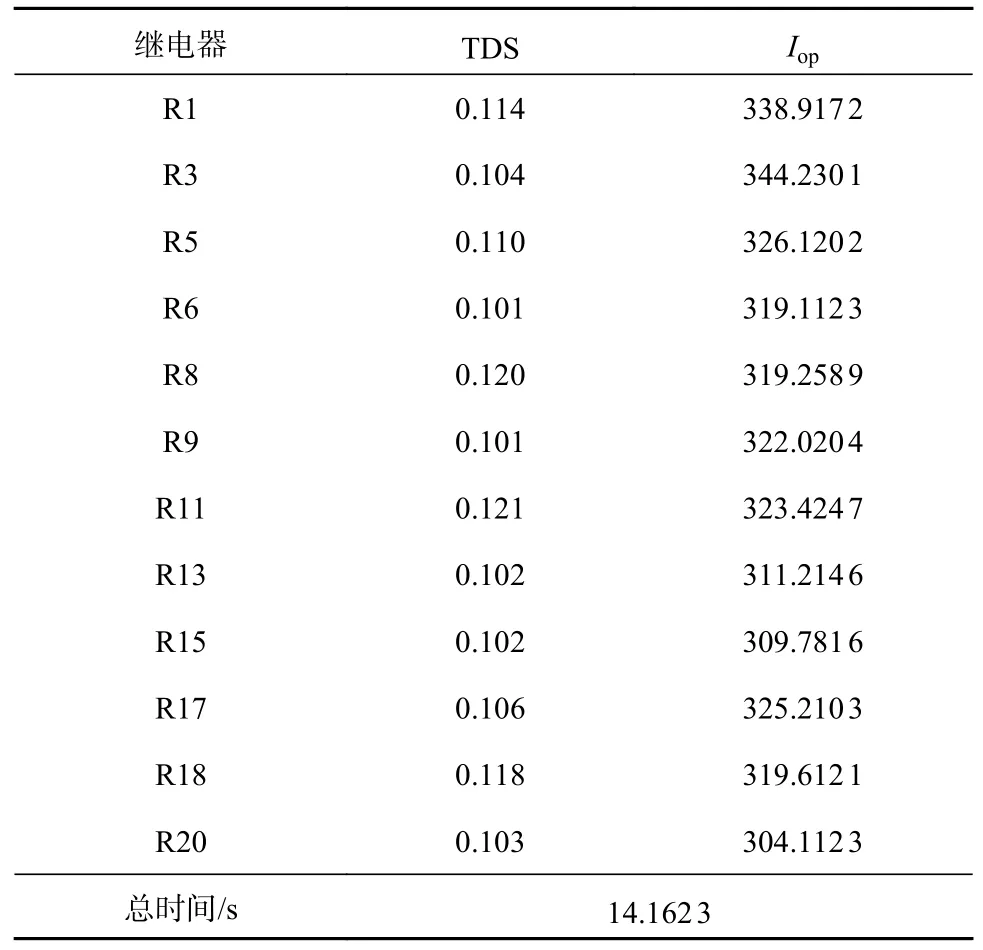
表8 DE-PSO 算法的求解结果
从3 组仿真结果中可以看出,整定系数TDS、继电器的启动电流Iop均能满足约束条件。基于A-PSO 算法、A-DE 算法、DE-PSO 算法的总动作整定时间分别为17.962 7、18.564 2、14.162 3 s。与A-PSO 算法、A-DE 算法的优化结果相比,采用DE-PSO 算法求解反时限过流保护定值整定模型能够寻找到更合理的整定系数TDS、启动电流Iop,同时,DE-PSO 算法能够跳出局部最优解,搜索到更短的反时间继电器的动作整定时间,保证了动作的速动性。
4 结论
1)为了增加迭代过程中的种群多样性,避免个体陷入局部最优解,将DE 算法与PSO 算法相结合,提出一种混合算法,并采用4 个带有多个局部最优位置的基准函数测试该算法的性能,其结果验证了混合算法的适用性和可靠性。
2)建立了反时限过流保护定值整定优化模型,将电网系统总的动作时间最小作为优化目标,在满足时间级差、时间整定系数、继电器最小动作时间等约束的情况下,采用A-PSO 算法、A-DE 算法、DE-PSO 算法分别求解模型。其仿真实验结果表明,DE-PSO 算法能搜索到更优的反时间继电器的动作整定时间,能充分保障继电器动作的速动性。

