考虑多目标优化模型的风电场储能容量配置方案

陈晓光，杨秀媛，王镇林，王浩扬

（北京信息科技大学自动化学院，北京市 海淀区 100192）

0 引言

2021年1—11 月，全国发电装机容量约23.2亿kW，同比增长9.0%，其中，风电装机容量约3.0亿kW，同比增长29%。风力发电具有随机性、波动性较大等特点，这给风电并网带来很多问题，如系统的稳定性、电能质量、系统发电计划和调度等[1-5]。储能系统拥有快速存储和及时释放电能的双向吞吐功率能力，这种能力具有灵活、快速的特点，且过程中不需要风电机组的控制[6-8]。在实际工程中，受地理位置、技术和经济等多方面的制约，储能系统无法无限满足电力系统的需求[9-11]。储能系统成本与功能存在相互制约关系，所以在储能系统配置过程中，考虑运行功能性的同时引入经济效益分析更合理。

关于储能系统优化配置，研究者做了大量工作，并取得了一定成果[12-16]。储能系统优化配置为高维非线性优化问题，传统方法的求解难度较高，储能系统配置模型的搭建以及根据模型选取合适的智能算法至关重要[17-19]。当前研究中储能系统功率和容量的配置主要采用模型求解法[20-21]，即基于对研究问题的需求不同，建立不同的数学模型(目标函数和约束条件)，同时又根据目标函数个数分为单目标模型、多目标模型。

文献[22]建立了单目标经济模型，以运行成本、惩罚成本和固有成本3部分费用现值最小作为目标函数；文献[23]中建立了全寿命周期的单目标经济模型，完善了全寿命周期模型目标函数，加入了报废处理成本，并对不同配置方案进行了经济性评估和灵敏度分析。以上两者虽然对储能系统进行了经济分析，但经济组成部分忽略了配置储能系统后的效益分析。文献[24]为了平抑风电波动，利用概率数理统计计算出最优的混合储能容量配置，虽然有很强的理论支持，但过于侧重储能的功能型效果，弱化了储能成本对储能推广的影响，无法兼顾经济性和功能性。文献[25]提出一种光热-抽水蓄能-电池复合储能系统容量多目标优化模型，以混合储能系统效益最大和等效负荷方差最小作为目标函数，利用粒子群算法进行求解；文献[26]顶层模型以年综合成本费用年值最小为目标函数，底层模型以日惩罚成本最小为目标函数，利用粒子群算法对双层模型进行迭代求解。以上两者都考虑了功能性和经济性目标，但其所建立模型维度较高，计算复杂，利用传统的粒子群算法进行求解，可能会陷入局部最优。

基于以上分析，现阶段储能配置存在以下问题：一是在经济性分析上过于单一，经济模型中的组成部分划分不清晰，大多数研究仅考虑了投资成本和运维成本2部分，此外，效益模型仍不完善，忽略了储能系统投入使用后的直接收益和间接收益；二是不同储能容量对功能性和经济性的相关性研究多侧重于其中一方面；三是现有研究涉及的智能算法存在求解精度低、同一化等缺陷[27-31]。因此，建立一种考虑多目标优化的储能配置模型，完善模型中成本和效益的经济组成部分，并同时将功能性指标和经济性指标作为目标函数进行求解计算具有实际意义。

本文利用小波包分解将风电原始信号分频，得到混合储能系统的补偿功率，基于全寿命周期成本模型，完善其组成部分，建立了经济-应用多目标优化模型，利用改进概率变异粒子群优化(probabilistic mutation particle swarm optimization，PMPSO)算法求解模型的容量配置，并且引入熵权概念对Pareto解集进行归一化处理，得到最优储能配置方案，最后通过与多种配置方案进行对比分析，验证了求解得出的配置方案兼顾经济性和功能性。

1 基于小波包分解算法的功率分配

1.1 自适应小波包分解算法

风电功率可以通过小波包分解为不同频率的分量。低频分量变化平缓，波动性较小，其功率幅值较高；次高频分量和高频分量波动性强，其功率幅值小，基本上在零值左右波动。因此，风电场可以根据并网波动率的要求，选择合适的小波包分解层数n，将分解后的低频分量作为并网功率，次高频分量和高频分量则可以通过不同的储能装置来进行平抑。

分解层数n的选择：小波包分解层数n越大，并网目标功率曲线越平滑，所需配置的储能容量越大；n越小，低频并网信号波动率越大。因此，采用小波包分解风电功率，计算每个分界层数下低频分量的功率波动是否满足现行国家标准规定的风电场低频分量功率波动的最大限值。若满足并网要求，则停止循环，此时n为需要的分解层数；否则，继续加深分解层数，进而确定小波包最优分解层数[32-33]。

小波包算法由小波包分解和重构2个部分组成。分解过程如下：

式中：S2nn，0(t)、S2n+1n，1(t)分别为第n层小波包分解的低频分解系数和高频分解系数；an、bn分别为分解的低通滤波系数和高通滤波系数；Sn-1，0(t)为第n-1层小波包的重构信号。

重构过程如下：

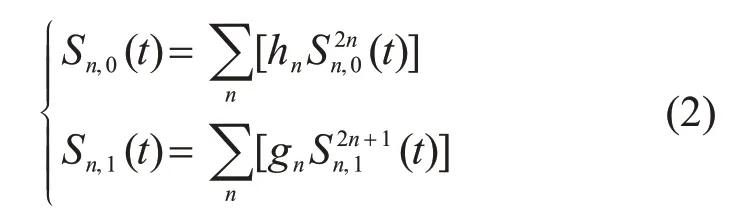
式中：Sn，0(t)、Sn，1(t)分别为小波包重构的低频信号和高频信号；hn、gn分别为重构的低通滤波系数和高通滤波系数。

经过n层小波包分解后，原始信号被分解成2n个频段，每个频段的带宽为f0=fs/2n+1，其中fs为采样频率。第m个小波包频段为[mfs/2n+1，(m+1)fs/2n+1]。

1.2 混合储能系统功率分配

小波包分解后的低频分量P(n，0)作为并网目标功率，其余高频分量P(n，1)～P(n，2n-1)则为风电功率的波动分量，由混合储能装置来平抑，即

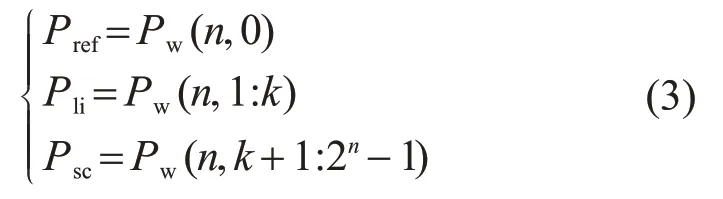
式中：Pref为并网功率；Pli、Psc分别为锂离子电池、超级电容补偿功率，其值大于零时表示充电，小于零时表示放电；Pw(·)为各频段重构后对应功率；1:k、k+1:2n-1表示频带区间范围，其中k为高频分段数。

2 混合储能优化配置模型

本文基于全寿命周期成本，利用费用年值法[34]对储能系统整个生命周期内产生的所有费用建立经济性模型，以净收益最大、波动量最小和弃风量最小为目标函数，对储能系统容量进行优化配置。

2.1 优化配置模型

模型主要对项目周期T年、基准折现率为i0的储能系统初期购置阶段、运行阶段和报废处理阶段的成本与收益进行分析。需要指出的是，对于混合储能系统，锂离子电池和超级电容的计算方式相同，因此本文只列举锂离子电池的计算公式。

1）初期购置阶段

初期购置成本主要由初始投资资金与辅助设备资金构成，由储能系统的额定功率和额定容量决定，可表示为

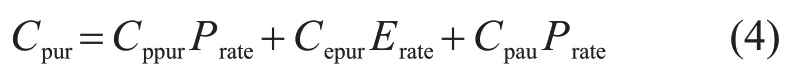
式中：Cpur为初期购置成本；Cppur为单位功率投资成本；Cepur为单位容量投资成本；Cpau为单位功率辅助成本；Prate为储能额定功率。

2）运行阶段

运行阶段成本主要由运行维护成本、置换成本和惩罚成本构成。运行维护成本Com主要由固定维护成本和可变维护成本2部分构成，如式(5)所示，其中，固定维护成本与储能额定功率Prate有关，与日常运行状态无关；可变维护成本与年充放电量Wess有关。

式中：Cpom为单位功率运维成本；Ceom为单位电量运维成本；Preffact为风电实际并网功率；Pw为原始风功率；Δt为采样时间；N为一年内的采样点个数。考虑到原始数据长度的局限性，这里Wess代表项目周期的年均充放电量。

置换成本表示为

式中：Cpex为单位功率置换成本；nex为置换次数，nex=T/Ln，Ln为储能等效循环寿命，由雨流计数法折算得出。

惩罚成本由缺电惩罚成本和弃风惩罚成本组成。其中，缺电惩罚成本表示为

式中：αlack为单位能量缺电惩罚系数；Elack为年缺电量，表示为

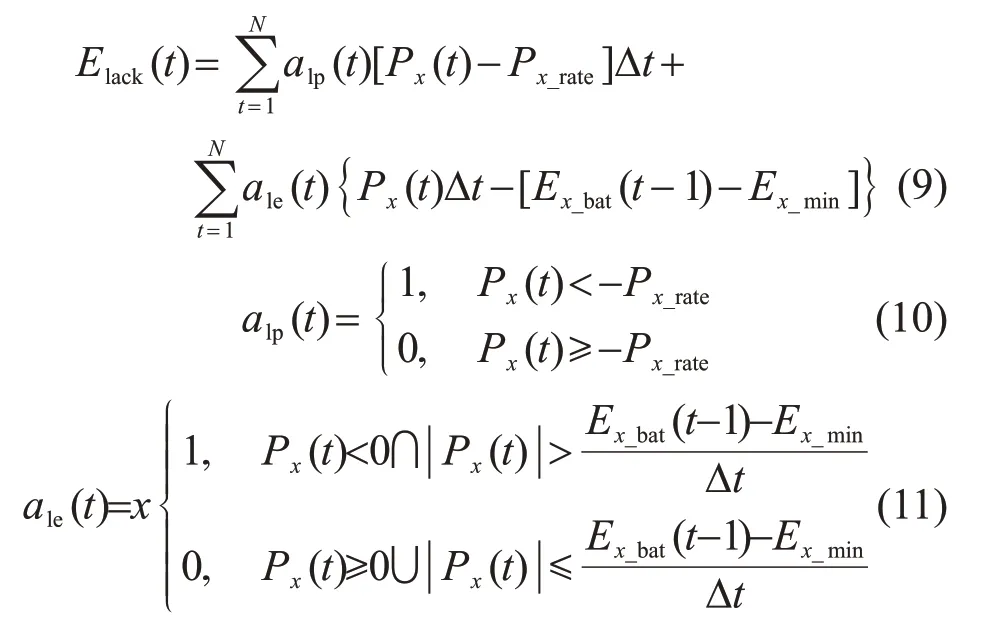
式中：x为不同储能介质；Px为x储能系统的补偿功率；Ex_bat为x储能系统的补偿值；Px_rate为x储能系统的额定功率值；Ex_min为x储能系统的安全容量最小值；alp、ale为缺电布尔值，其值为1时表示缺电。考虑到原始数据长度的局限性，这里Elack代表项目周期的年均缺电电量。

弃风惩罚成本表示为

式中：αab为单位能量弃风惩罚系数；Eab为年弃风量，表示为

式中：Ex_max为x储能系统的安全容量最大值；abp、abe为弃风布尔值，其值为1时表示弃风。考虑到原始数据长度的局限性，这里Eab代表项目周期的年均弃风电量。

3）报废处理阶段

该阶段成本由报废处理成本和回收残值构成。其中，报废处理成本表示为

式中：Cpsc为单位功率报废成本；Cesc为单位容量报废成本。

回收残值表示为

式中δres为回收残值率。

综上，储能系统成本为

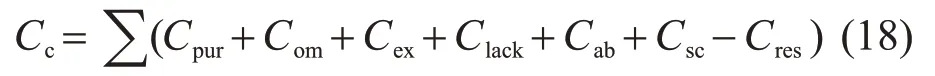
式中求和表示2种储能成本费用之和。

储能系统收益Iin包括风电场配置储能系统后的多发电量收益Imul、财政补贴的收益Isub和缓建并网通道的效益Ipass，表示如下：

式中：αmul为售电价；Eess为风电场配置储能系统后多发电量；αsub为补贴电价；kpass为并网通道的单位功率造价；Pb为混合储能系统补偿功率。

因此，储能系统的净效益现值为Inet=Iin-Cc，目标函数为

为表征储能系统平抑波动的功能效果，建立了波动量指标，即以并网风功率的波动量平方和为目标函数：

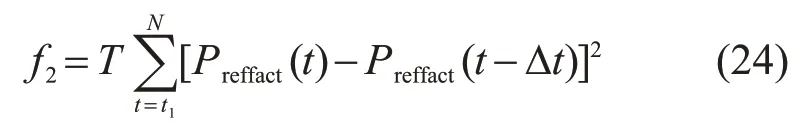
为表征储能系统减小弃风的功能效果，建立了弃风量指标，即以年平均弃风量为目标函数：

综上，储能系统优化配置模型为

储能系统有以下约束：

①额定功率约束。任意时刻下不同介质补偿值不能超过其额定功率值，即

②额定容量约束。任意时刻下不同储能介质的储能容量不能大于其额定容量，即

式中Px_c、Px_d分别为x储能系统的充、放电功率。

③荷电状态(state of charge，SOC)约束。

式中Sx_min、Sx_max分别为x储能系统的SOC最小值和最大值。

2.2 改进粒子群算法

传统粒子群算法存在易丢部分解、陷入局部最优解等缺陷。针对这些问题，基于自适应权重粒子群优化(adaptive weighted particle swarm optimization，AWPSO)算法，引入网格质量和非支配排序遗传算法(non-dominated sorting geneticalgorithm，NSGA-II)[35]和PMPSO算法中的变异、精英库操作，对变异概率进行局部非均匀动态更新，提出一种改进PMPSO算法，并与文献[31]中自适应量子粒子群优化(adaptive quantum particle swarm optimization，AQPSO)算法进行比较。

2.2.1 AQPSO算法

相对于传统的粒子群优化(particle swarm optimization，PSO)算法，量子粒子群优化(quantum particle swarm optimization，QPSO)算法不再关注粒子的移动速度，只考虑粒子位置。在QPSO算法中，粒子位置的更新方程为：

式中：xid为第i个粒子位置，其中d为粒子维度；φid、uid为服从[0,1]上均匀分布的随机数；pid=(pi1，pi2，…，pid)为第i个粒子迭代计算的吸引因子；Lid为粒子在某一相对点位置的概率；Pid为个体历史最优；Pgd为全局最优点；E为单位矩阵。

式中：ρ为收缩扩张系数；mb为当前粒子的个体平均最优点；m为种群粒子数。

从参数自适应以及最优权重分配方面对QPSO算法进行改进，加入自适应中心权重思想，构成归一化权重向量：

式中：fid、fidb分别为当前位置的适应度数值和最优粒子适应度数值；wid为中心权重系数，即每个粒子对平均粒子最优的权值，以提高全局搜索能力。

改进收缩扩张系数的制定规则：

式中：ρte、ρ0分别为收缩扩张系数的末值与初值；gen、genmax分别为当前迭代次数和最大迭代次数。

2.2.2 PMPSO算法

AWPSO算法速度与位置更新方程如下：

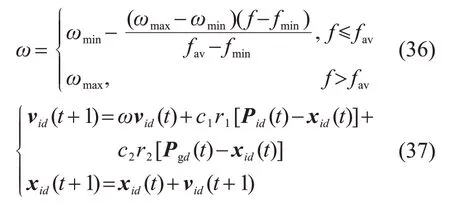
式中：ωmax、ωmin分别为非负数的惯性权重ω可取的最大值和最小值；f为微粒当前的目标函数值；fav、fmin分别为当前空间中微粒的平均目标值和最小目标值；c1和c2为非负数的学习因子；r1和r2为服从[0,1]上均匀分布的伪随机数；vid为微粒速度，取值范围为[-vmax，vmax]，其中vmax为微粒最大速度，是常数，根据工程需求自行设定。

动态更新权重，使其在飞行寻优中避免局部最优点，但忽略了初始化粒子时导致的分布不均匀问题，也没有改善粒子群算法普遍容易丢失个别解的缺点。针对以上问题，引入网格质量和非支配排序遗传算法中的变异、精英库操作，网格质量用来表示粒子在飞行过程中某局域的搜索质量水平，某一区域粒子越多，网格质量就越低，说明该区域已经搜索较为完全，无需继续寻优，可通过变异操作对未开发的区域进行精确查找。对PMPSO引入局部非均匀操作，动态更新变异概率，基本原理如图1所示，将种群均匀分成m等份，对m等份进行不同变异操作：第1部分不变异；第2部分到第m-1部分为定概率的均匀变异；第m部分为不均匀变异。由于随着迭代次数的增加，寻优范围应更精细，变异的粒子数不应过多，因此概率随迭代次数动态变化，表示如下：

图1 概率变异示意图Fig.1 Schematic diagram of probability variation

式中：Pper_mut为第gen代的变异概率；nvar为变量个数。

PMPSO算法具体步骤如下：

1）赋值相关算法参数，对种群以及粒子进行初始化，并将初始适应度存入精英库。

2）初始化个体最优Pbest及全局最优Gbest，并存入精英库，记录粒子具体信息。

3）定义网络计算拥挤度，计算网格质量Q；

4）开始主循环，利用网格质量更新选择个体最优Pbest，若空间不够，则可以进行缩减。

5）对粒子进行飞行寻优操作，更新粒子速度、位置及权重，计算适应度函数值。

6）对种群进行概率变异操作，同时核验边界。

7）根据支配关系，比较粒子新位置和局部最优位置的优劣，更新每个粒子的局部最优Pbest与全局最优Gbest，并存入精英库。

8）更新网格，计算网格质量，同时更新精英库。

9）判断是否达到最大迭代次数或满足设定的条件，若不满足，则跳转至步骤4）；否则，结束程序并输出存档中的最优解集。

2.3 多目标优化结果处理

本文提出的风电场储能优化配置模型基于智能算法得出的Pareto解集基于优劣解距离(technique for order preference by similarity to ideal solution，TOPSIS)法进行改进，对解集中每个解的优劣程度进行评判，得出综合满意度最高的熵权最优解。具体步骤如下：

1）对目标函数进行归一化处理，将波动量、成本、总收益和弃风量作为影响因子引入。

式中：δi，q、fi，q分别为第i个解在第q个目标上归一化后的值与实际值；fi，max、fi，min分别为第i个目标的最大、最小值。

2）求各影响因子的权重。

式中：Wq为第q个影响因子的信息熵；np为Pareto前沿解的个数；τq为第q个影响因子的权重；y为影响因子的个数。

3）计算综合满意度。

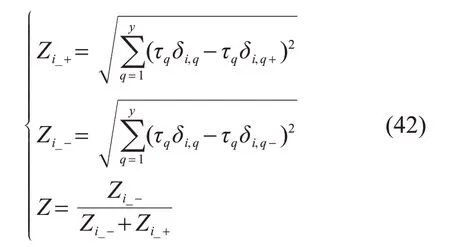
式中：Zi_+、Zi_-分别为个体i的正、负理想尺度；δi，q+、δi，q-分别为归一化后个体i对应的最大、最小值；Z为熵权拟合度，其值越接近1，说明影响因子综合满意度越高。

4）取熵权拟合度最高值对应的熵权最优储能容量配置方案。

本文提出的储能优化配置流程如图2所示。

图2 储能优化配置流程图Fig.2 Flow chart of energy storage optimization allocation

3 算例分析和仿真验证

3.1 评价参数

为了进一步量化储能系统效果，可以用以下参数衡量：

1）波动量裕度χ。

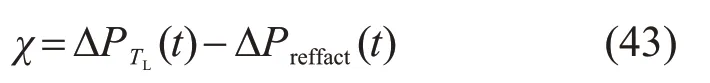
式中：ΔPTL(t)为时间尺度为TL时允许的最大波动量，TL一般取1 min或10 min；ΔPreffact为经运行策略实际并网的最大波动量。

2）储能系统因额定容量限制而无法按预补偿值工作的百分数ε。ε值越小，说明储能系统输出功率分配越合理。

式中：Tbat为储能系统补偿工作时间；al(t)为缺电决策变量，其值为1时，表示储能系统因容量限制而无法继续放电的缺电状态；aab(t)为充电决策变量，其值为1时，表示储能系统因容量限制而无法继续充电的状态。

3）储能等效循环寿命Ln。对于功率型储能，其循环使用次数可达10万次，与充放电深度(depth of discharge，DOD)关系不明显，且使用寿命远高于能量型储能，因此本文着重考虑能量型储能。

采用雨流计数法计算DODx(表示储能系统充放电深度为x)，电池第x次循环的等效循环系数为

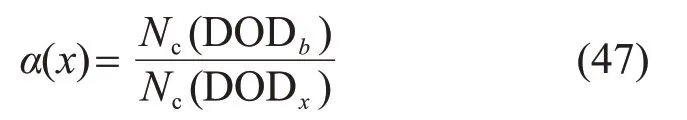
式中：DODb为基准放电深度，b=1；Nc(DODb)、Nc(DODx)为对应的循环使用次数。

电池工作1个工作周期Y内，DODx对应的循环个数为mx，共有Ncd个放电深度。则在周期Y内电池消耗的寿命为

Yy为采样数据时间长度，本文取1 a，则电池的运行年限Ln为

3.2 算例仿真

3.2.1 仿真数据准备

由1.1节方法确定小波包分解层数n：采用db6小波对风电功率进行2层分解后，低频分量功率波动最大值为7.68 MW，因此2层分解不满足要求；对风电功率进行3层分解后，低频分量功率波动最大值为3.15 MW，满足风电并网要求，最终确定小波包分解层次为3层。再对原始信号进行FFT变换，得出其幅频特性曲线，发现当频率大于1.54 mHz时，幅值接近于0，说明能量很小，因此可将该频率作为锂离子电池和超级电容的界限。

算例数据为某风电场一年的历史数据，额定功率为50 MW，优化模型相关参数见表1、2；改进PMPSO相关参数，种群规模设为200，迭代次数设为100次，个体、群体自信度均为1.5，初始变异概率为0.5。

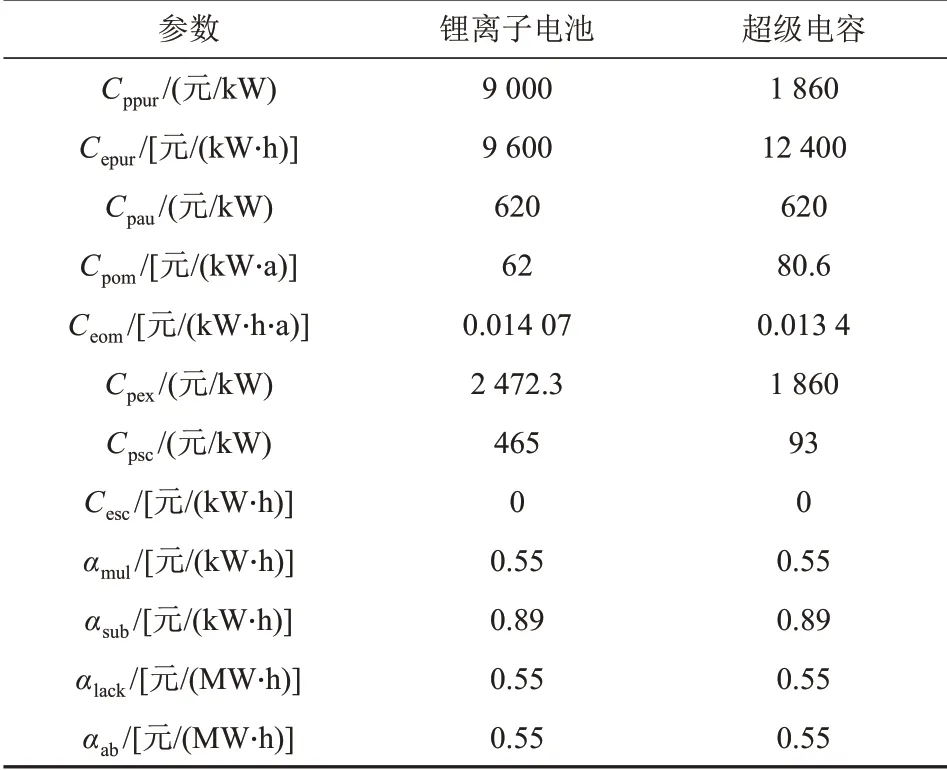
表1 储能经济参数Tab.1 Energy storage economic parameters

表2 相关技术参数Tab.2 Relevant technical parameters

3.2.2 熵权最优配置方案的验证

利用改进PMPSO算法求解风电场储能配置模型得到的Pareto解集如图3所示，该图表征了3个目标函数f1、f2、f3随自变量(额定功率和额定容量)变化的趋势，同时也直观地展示了3个目标函数之间的变化关系。此外，根据Pareto前沿解的个数均匀取出7个解进行定量分析，结果如表3所示。

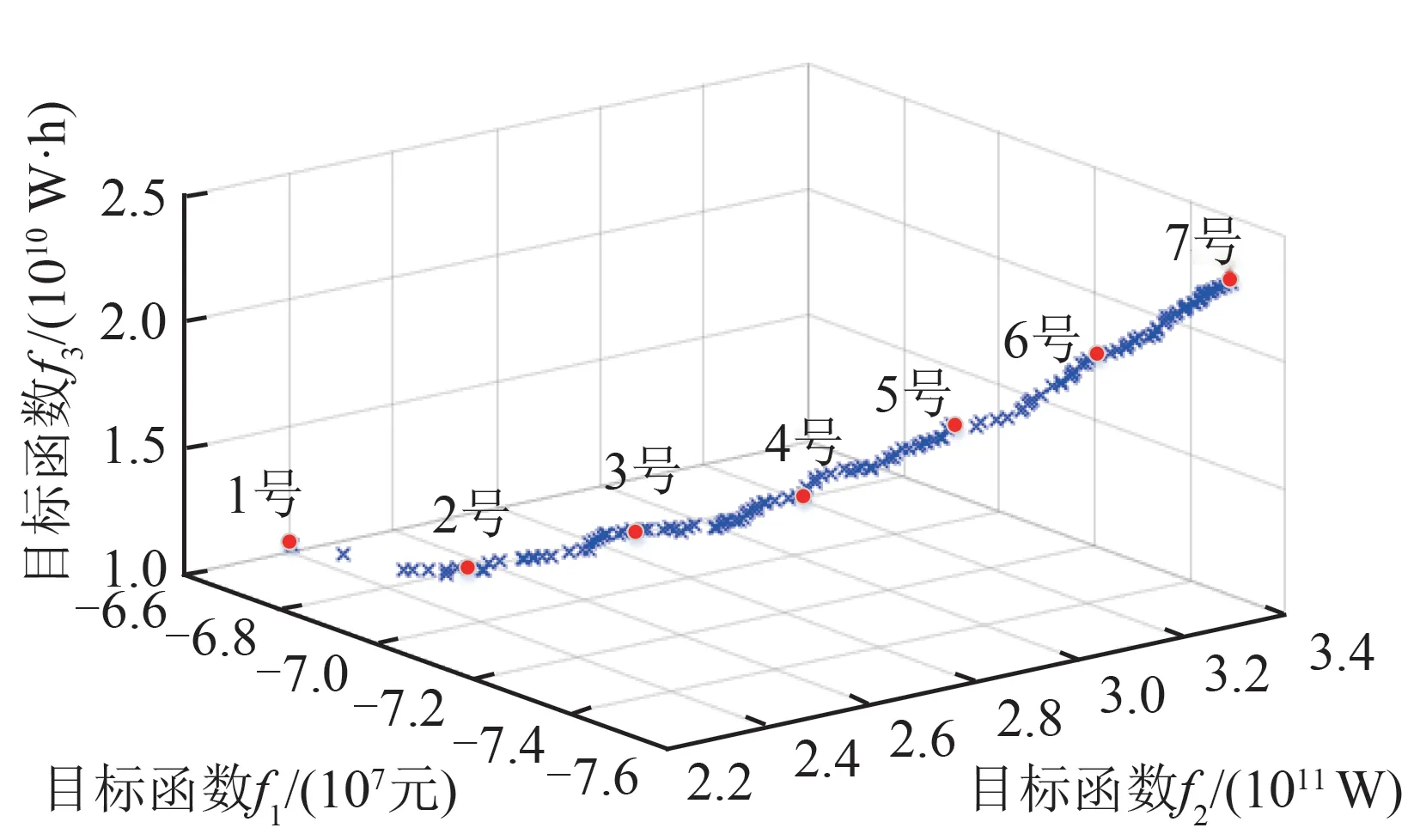
图3 改进PMPSO算法的Pareto解集Fig.3 Pareto solution set of improved PMPSO algorithm

多目标优化侧重探究解的多样性，通过表3可以得到，1—7号方案储能容量逐渐减少，由1号配置方案的10.089 MW/14.991 MW·h到7号配置方案的5.003 MW/7.559 MW·h。Pareto典型配置方案目标函数值如图4所示，不同方案成本和总收益曲线如图5所示。

表3 改进PMPSO Pareto部分解集Tab.3 Partial solution set of improved PMPSO Pareto

图5 不同方案成本和总收益曲线Fig.5 Cost and total benefit curves of different schemes

结合图4、5可知，随着容量的减少，成本和总收益均减小，目标函数f1减小(即净收益增大)，说明储能成本对储能系统净收益影响更大，对应的波动指标(目标函数f2)、弃风指标(目标函数f3)均逐步上升，即平抑效果变差、弃风量增大。1号方案净收益最小，波动指标和弃风指标均最低，是偏向功能性的风电场储能配置方案；7号方案净收益最大，波动指标和弃风指标均最高，是偏向经济性的风电场储能配置方案。

图4 Pareto典型配置方案目标函数值Fig.4 Objective function values of Pareto typical allocation schemes

为了得到兼顾功能性与经济性的配置方案，利用2.3节的方法求得熵权最优方案，定义为8号方案(7.613 MW/11.329 MW·h)，1、7、8号方案的容量配置和评价参数分别如表4、5所示。图6、7分别为3种配置方案下风电日运行曲线和储能系统功率，图6中并网功率上方的黄色阴影面积为弃风量。

图6 1、7、8号方案日运行曲线Fig.6 Daily operation curves of scheme 1,7,8

结合表4、5可以得出，随着配置比例的增加，黄色阴影面积依次减小，说明弃风量逐渐减少，同时因功率和容量限制而不能工作的情况在减少，8号方案的成本、总收益、净收益、波动指标和弃风指标均处于1号、7号方案之间。相较于7号方案，8号方案的成本增加了2%，净收益减小了2.7%，弃风量下降了34%，最大波动量下降了近50%，运行年限由9.52 a提升到10.32 a，说明8号方案用较小的成本增量换取了较大的功能效果。相较于8号方案，1号方案的成本增加了6.4%，远高于8号相较于7号的成本增幅，但弃风量下降了30%，近似于8号相较于7号的弃风量降幅，运行年限相似，说明1号方案虽然有较大的成本增量，但波动量和弃风量指标并未大幅度减少，因此配置不同比例的储能系统弃风量差异不大时，无需配置更大容量的储能系统去进行平抑，可以通过降低波动量裕度使成本下降。此外，3种方案的熵权拟合度中8号方案最大，其值为0.995，从而验证了熵权最优方案是兼顾功能性和经济性的最优配置。

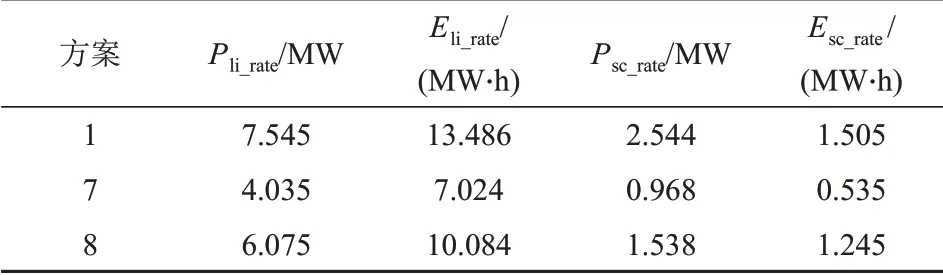
表4 1、7、8号方案的容量配置Tab.4 Capacity configuration of scheme 1,7,8

表5 1、7、8号方案的评价参数Tab.5 Evaluation parameters of scheme 1,7,8

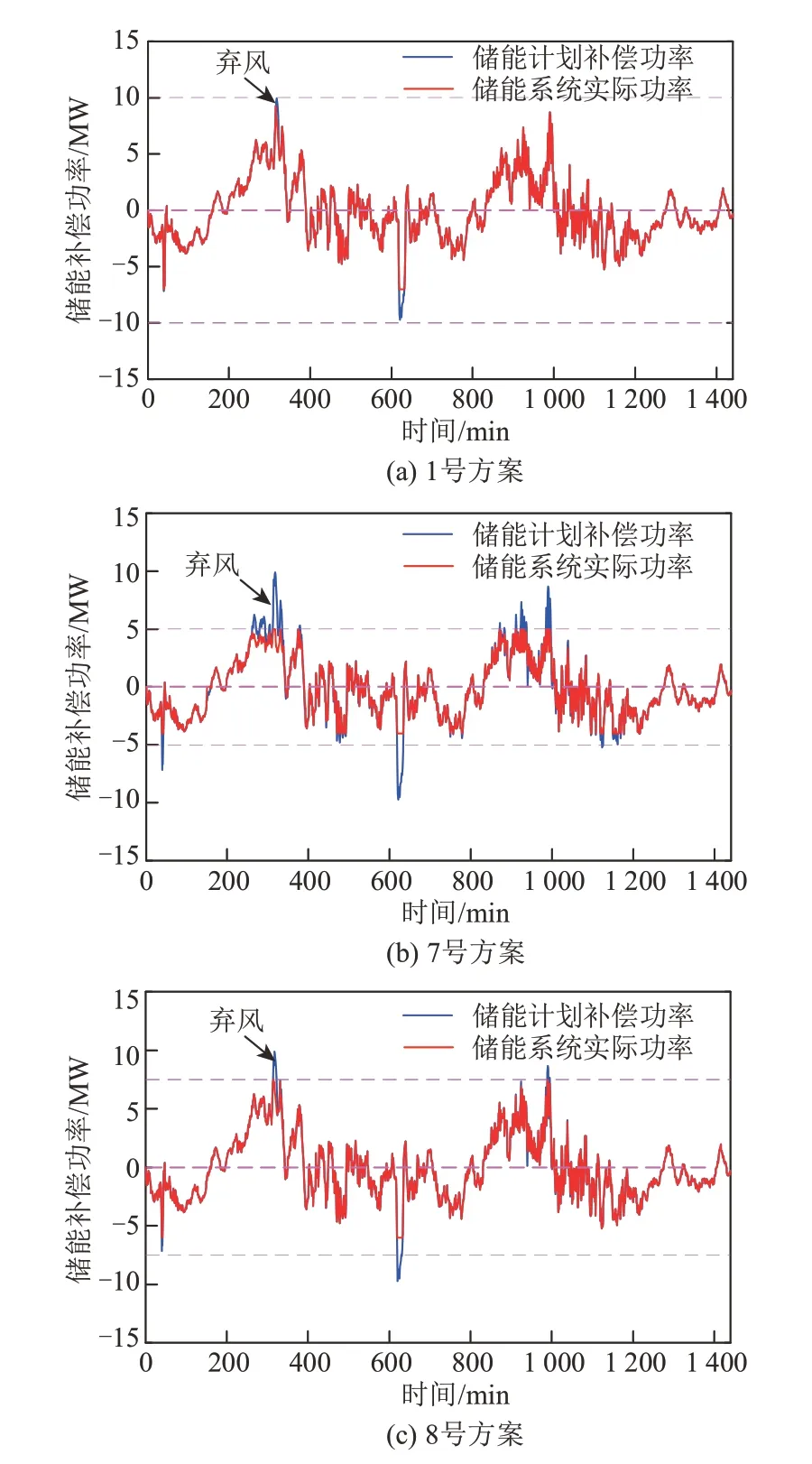
图7 1、7、8号方案储能系统功率Fig.7 Energy storage system power of scheme 1,7,8

3.2.3不同算法的熵权最优配置方案对比

由于文献[31]已经验证AQPSO算法寻优能力远大于AWPSO算法，因此该算例只对AQPSO算法和改进PMPSO算法进行对比分析。通过上文分析可知，波动指标和弃风指标具有相同的变化趋势，因此为了直观展示不同目标函数之间的关系，取目标函数f1为纵坐标、目标函数f2为横坐标的二维图进行分析，结果如图8所示。

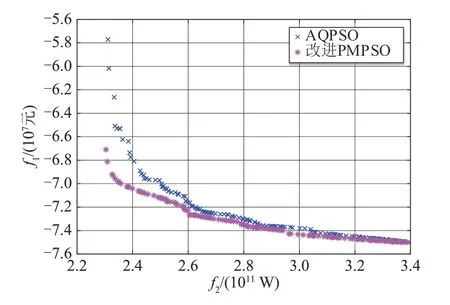
图8 不同算法Pareto最优解集Fig.8 Pareto optimal solution sets of different algorithms

多目标优化不仅关注解的多样性，还关注解的收敛性。将AQPSO算法得到的熵权最优方案定义为9号方案。结合图8可知，由于AQPSO算法寻优能力比改进PMPSO算法弱，AQPSO算法寻优过程中，在目标函数f2=2.4×1011W附近陷入局部最优，导致求得的储能配置方案容量比改进PMPSO算法求得的容量大，如表6所示。8、9号方案的评价参数如表7所示，图9为8、9号方案风功率和储能补偿功率日运行图。

表7 8、9号方案的评价参数Tab.7 Evaluation parameters of scheme 8,9

结合表6、7和图9可以看出，2种方案因功率和容量限制而导致无法工作的比例均较小，在最大波动量、波动指标、弃风指标和运行年限多个参数值上相差不大，9号方案成本增加了15%，而8号方案在经济性占优的情况下，与9号方案的波动指标、弃风指标接近，并且储能配置容量减少了18%，说明了本文算法求得的配置方案的有效性和优越性。

表6 8、9号方案的容量配置Tab.6 Capacity configuration of scheme 8,9

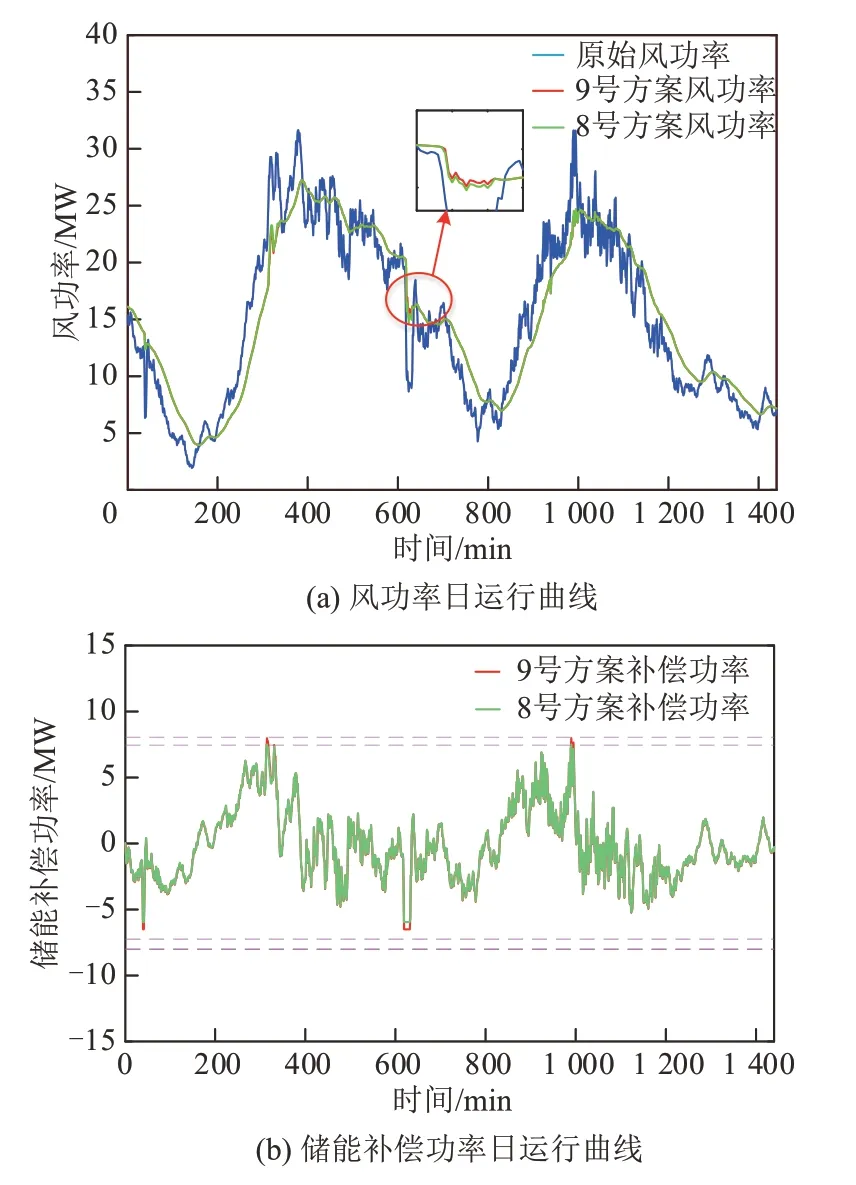
图9 8、9号方案风功率和储能补偿功率日运行图Fig.9 Daily operation diagram of wind power and energy storage compensation power of scheme 8,9

4 结论

1）基于全周期寿命成本模型，建立了净收益最大-波动量小-弃风量小的多目标储能配置模型，引入熵权概念对Pareto配置方案解集进行熵权拟合度评估，得出的熵权最优配置方案相较于单目标配置方案能够平衡功能性和经济性需求。

2）与AQPSO算法相比，改进PMPSO算法在高维问题求解方面有更好的寻优能力和求解速度，求解得到的熵权最优配置方案波动量裕度减小了6%，保证了波动量满足要求、弃风量较小的同时，配置容量减小了18%，净收益提高了4.6%，表明该方法有效可行。

以上所得储能系统补偿功率和配置方案均是基于风电场的历史数据，后续将围绕风功率精确预测及储能配置影响因素的灵敏度开展研究。