7075 铝合金铣削参数多目标优化

齐 萌

（开封技师学院，河南 开封 475000）

0 引言

7075 航空铝合金由于具有优异的机械性能，被广泛应用于高端制造业中［1］。然而，在对其进行加工的过程中，通常不能同时兼顾加工质量和加工效率。特别是当工艺参数优化程度较低时， 一定程度上会降低加工效率，同时恶化了工件的表面质量。 比如，进给量过大致使工件表面出现严重的隆起和凹坑，主轴转速较小容易产生积屑瘤等不良现象。因此，合理选择加工工艺参数是保证铝合金精密件高质量、高效率加工的重要前提。

长期以来， 许多学者在参数优化方面进行了研究。 施志辉等采用计算简洁的直接求导法得出最优区间，但该方法由于要求目标函数必须连续可导，所以实用性较低［2］。 Wang J 等运用神经网络算法对参数优化区间进行了合理的分割， 但对于离散度大的样本，应用该方法容易陷入局部最优解［3］。王剑彬等利用粒子群法快速确定参数的最优区间， 但由于人工干预多，推理速度缓慢［4－5］。 张颂等运用遗传算法得到了较优的工艺参数，但该方法计算较为耗时［6］。Yan 等运用响应曲面法和灰色关联度进行工艺参数建模，但该方法计算较为烦琐［7］。Kant 等采用关联柔度法寻求参数最优解， 但其结果的可靠性还需进一步提升［8］。 邓朝晖等在考虑信噪比因子的基础上采用组合权重灰色关联分析法对其参数进行求解，但该方法的人为权重较高［9］。

为了获得7075 铝合金铣削表面粗糙度与工艺参数的内在映射规律，笔者采用方法灵活、运算简单的多目标线性规划法建立数学模型， 根据实际需求设定目标函数的最优解和期望值［10］。与此同时，结合铣削试验， 利用超景深工具显微镜观察工件微观形貌，分析切削速度、侧吃刀量、主轴转速和背吃刀量等参数对7075 航空铝合金表面质量的内在映射规律，运用非线性回归分析方法，以最小表面粗糙度和最大材料去除率为目标函数， 建立铣削加工多目标优化的数学模型。 采用多目标线性规划法寻找最优解，并通过试验对最优解进行验证，最终为实际加工提供可靠的理论依据。

1 实验装置及方案设计

1.1 试验方案

本试验采用VDL－800 四轴加工中心机床，刀具为Φ20 三刃高速钢铣刀。试验材料为7075 铝合金，构件长100 mm、宽100 mm、高50 mm。 材料去除率通过切削时间和材料去除量确定。

1.2 试验设计及结果

为了充分体现工艺参数对7075 铝合金铣削表面粗糙度Ra和金属材料去除率RMR的影响，以铣削表面粗糙度和加工效率为试验指标，以主轴转速n、切削速度vf、 背吃刀量ap和侧吃刀量ae为影响因素，采用正交试验法设计试验，其试验参数和结果分别如表1 和表2 所示。

表1 试验参数Tab.1 Parameters of experiments

2 工艺参数对表面质量的影响

2.1 工艺参数对表面粗糙度的影响

根据表2 可知， 表面粗糙度随着加工效率的增大而逐渐被恶化。 采用单因素分析法进一步对工艺参数与表面粗糙度的内在影响规律进行研究， 结果如图1 所示。

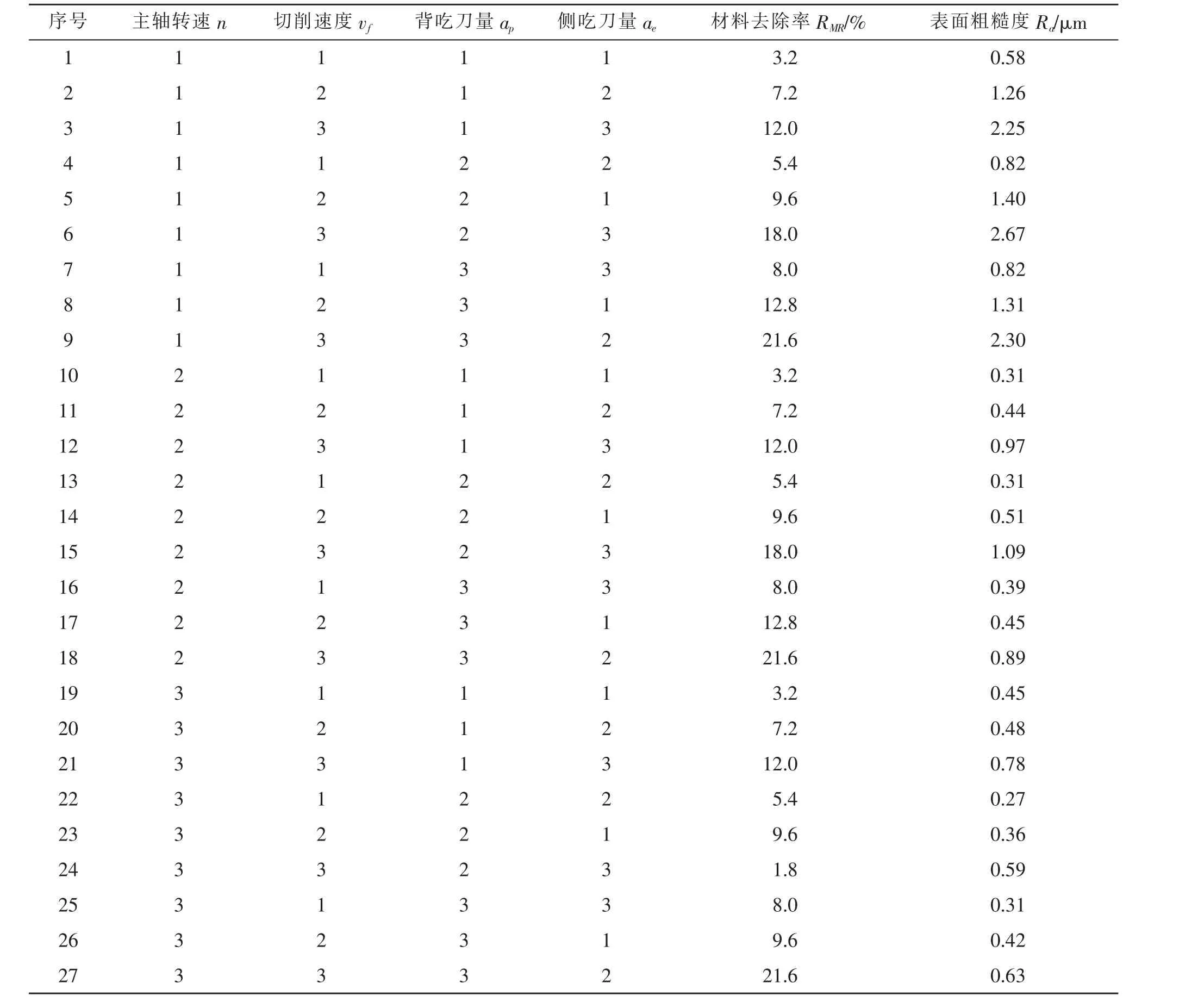
表2 试验结果Tab.2 Results of experiments

由图1 可得，当切削速度为400 r／min、背吃刀量为4 mm、侧吃刀量为9 mm 时，表面粗糙度随着主轴转速的增大呈恶化趋势； 当主轴转速为2 000 r／min、侧吃刀量为9 mm 时，随着切削速度和背吃刀量增大，表面粗糙度均被恶化，并且切削速度最为显著。特别是，当主轴转速小于1 500 r／min、切削速度大于400 mm／min 时，表面粗糙度均高于1.5 μm，严重恶化了工件的表面质量。这是由于7075 铝合金具有良好的塑性，在转速较低的切削过程中，挤压加工特性显著，增加了切屑与刀具的摩擦，从而产生“粘刀”现象。 再者，低转速切削对抑制积屑瘤的产生并不显著，使得切削瘤反复繁衍与湮灭，致使工件表面出现凸凹不平现象。 因此，适当提高主轴转速，可增强工件与刀具的切削分离特性，从而遏制“粘刀”现象的产生。 与此同时，在图1 给定的铣削参数内，随着切削速度的增加，表面粗糙度呈现增大趋势，然而随着主轴转速的提高， 切削速度对表面粗糙度增大的趋势逐渐减小。这又表明：表面粗糙度受主轴转速的抑制作用比切削进给速度更为显著。另一方面，增大切削速度可以提升材料去除率， 但是增大切削速度的同时，单位长度下切削波纹周期增加，峰谷效应越发不均衡。侧吃刀量对表面粗糙度影响不明显。其原因在于，增大侧吃刀量，虽然实际的侧面切削深度被增大， 但是切削刀刃单位长度上的切屑并未发生变化。 因此， 在实际加工中建议选择较高的主轴转速、较低的切削速度和背吃刀量，以及刀具寿命允许范围内的大侧吃刀量来兼顾表面粗糙度和加工效率。

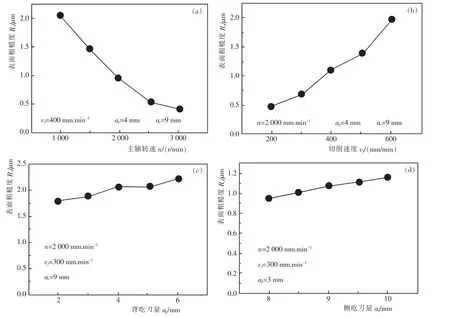
图1 工艺参数对表面粗糙度的影响Fig.1 Effect of process parameters on surface roughness

2.2 工艺参数对表面形貌的影响

由图1 分析可得，在其他加工参数不变时，切削速度对7075 铝合金铣削表面粗糙度影响最为显著。因此，选择了主轴转速为2 000 r／min、背吃刀量为4 mm、 侧吃刀量为9 mm 时， 切削速度分别为200 mm／min、300 mm／min、400 mm／min、500 mm／min、600 mm／min 时的表面形貌进行比较研究，得出了不同主轴转速下，7075 铝合金工件表面微观形貌的变化规律，如图2 所示。

由图2 可知，当主轴转速为2 000 r／min、背吃刀量为4 mm、侧吃刀量为9 mm 时，随着切削速度的增大，表面波纹度增大，且具有一定的周期性。 其原因在于当增大切削速度时， 相邻两刀痕重叠面积减小，虽然加工效率得到了大幅度提高，但是材料残留高度增大，沟壑宽度增加，峰谷效应明显。 特别是当切削速度大于500 mm／min 时， 由于刀具高速挤压材料，摩擦加剧，产生较大的摩擦热，刀具前角和后角磨损加剧。在这种情况下，一方面前角的减小使得刀具变钝，材料的撕裂现象加剧；另一方面，后角的减小加剧了刀具对已加工表面的摩擦， 形成压痕凹槽，对表面粗糙度造成一定的影响。

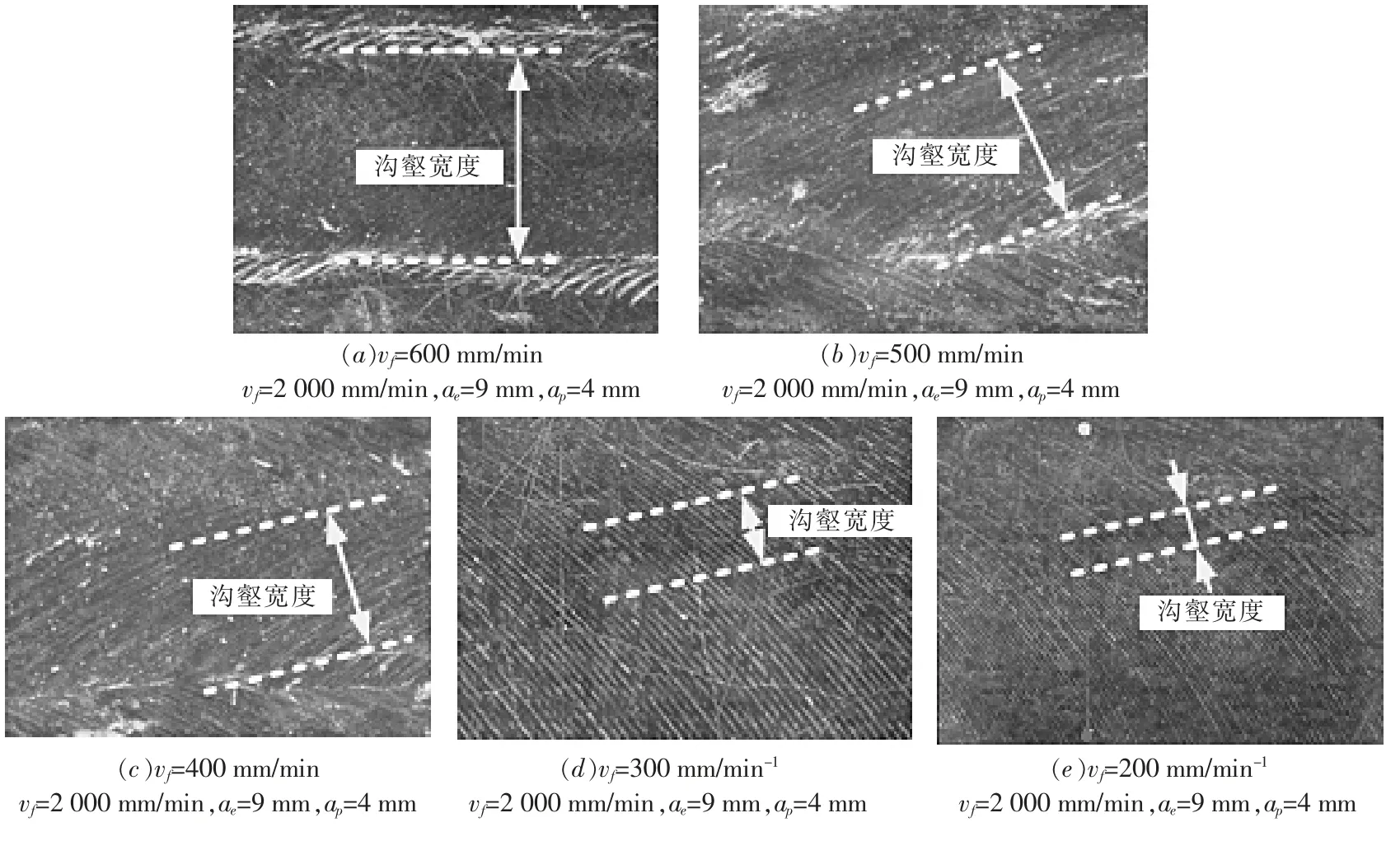
图2 不同切削速度下工件表面形貌Fig.2 Surface topography of workpiece at different cutting speeds

3 表面粗糙度预测模型的建立

衡量加工表面特性的重要指标为表面粗糙度，而切削用量的选择直接影响表面粗糙度。目前，工艺参数的确定通常是利用机械手册进行寻求， 或是技术工人凭着经验确定， 但是该方法与实际加工存在一定的差异。 因此，建立表面粗糙度预测模型，对表面粗糙度进行预测显得尤为重要。

对上述模型进行显著性检验可得：拟合度R2＝0.829 7，显著性检验F＝26.797 7＞0，说明模型拟合效果良好。为了进一步对预测模型的可靠度进行验证，笔者将试验样本作为验证数据点带入预测模型进行计算， 并将试验结果与预测值进行比对， 如图3 所示。

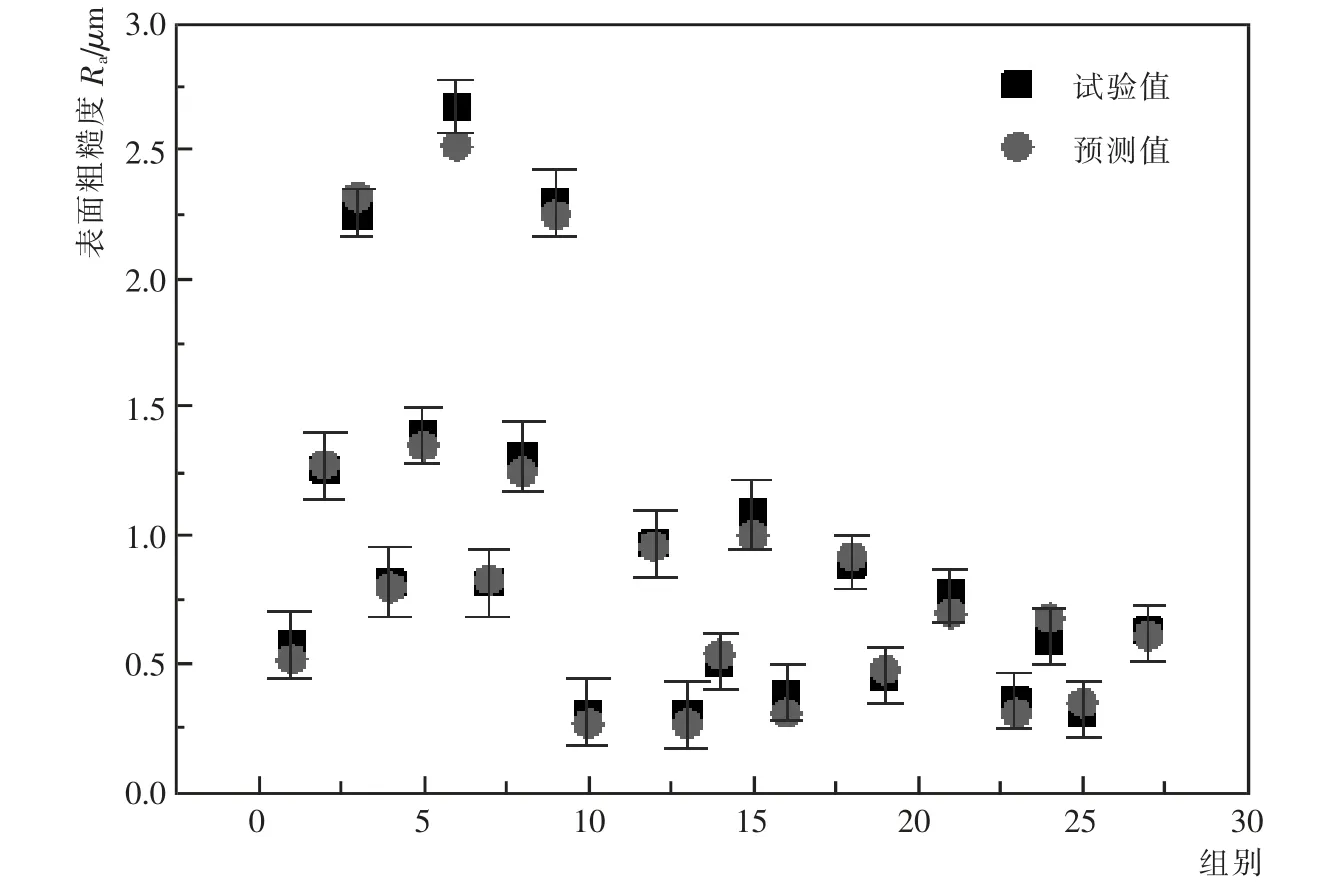
图3 预测模型的验证Fig.3 Validation of prediction models

由图3 可知， 预测模型输出值与表面粗糙度试验值最大误差分别为8.9%和8%。相对于试验结果，预测模型输出可靠， 即预测模型具有较高的预测精度， 从而为可控的表面粗糙度研究提供了一定的参考。进一步分析可得，在低速切削时的模型预测精度低于高速切削时的模型预测精度， 这是由于在高速切削状态下， 刀具与材料的粘连效应和材料的挤压撕裂效应被弱化。

4 工艺参数多目标优化

4.1 建立优化目标函数

本文所建立的多目标线性规划模型是以低表面粗糙度和高加工效率为指标建立的优化目标函数，具体如式（3）所示［12］。 最小表面粗糙度函数如式（4）所示。

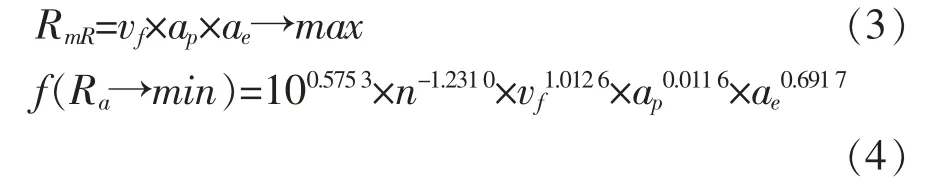
将式（4）进行线性化处 理，令X1＝lgvf，X2＝lgap，X3＝lgae，X4＝lgn，则式（3）转化为式（5）。 表面粗糙度模型转化为式（6）。

4.2 分析方法

多目标线性规划法由于模型简单，通用性较强，计算方便，摒弃了传统强化方法过于强调最优化，而在实际问题解决中其最优解很可能不存在的问题，它将优化问题和约束问题融为一体， 将性能指标与优化过程有机结合起来， 强调了满意而不是最优的思想，将多个目标函数进行线性约束［10］，可得式（8），约束条件如式（9）所示。

然后，求φ［Z（X）］的最小值，并将它的最优解X*作为上述模型的解。

4.3 求解

4.4 工艺参数最优解的验证

选择工艺参数n＝3 000 r／min，vf＝317 mm／s，ap＝4 mm，ae＝10 mm，预先加工出精毛坯试件，同时进行6 组试验，用表面粗糙度仪测得表面粗糙度（如表3所示）。

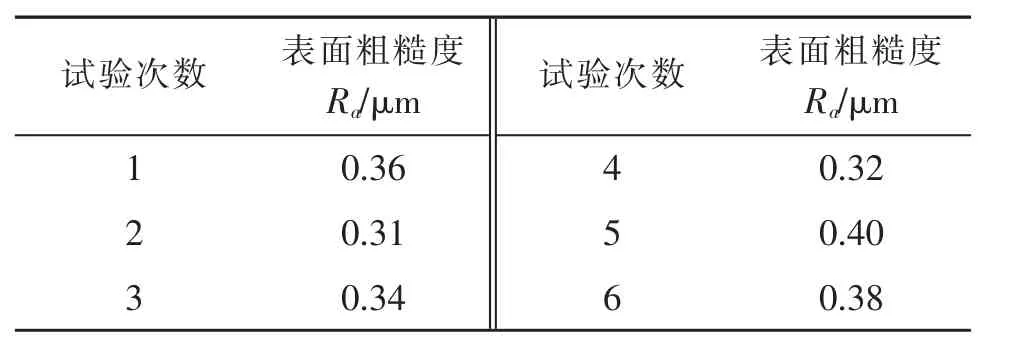
表3 试验数据Tab.3 Test data

由表3 可得， 表面粗糙度最小值为0.3 μm，最大值为0.4 μm，平均值为0.35 mm，最大值相对最优理论值的相对误差为17.6%， 最小值相对于最优解的相对误差为－11.7%，平均值相对于最优理论解的相对误差为2.9%。 这说明，最优解的理论值和试验值具有很好的一致性， 表面粗糙度模型具有较高的预测和指导作用。

5 结语

综上所述，根据显著性分析，本文采用回归分析方法建立的表面粗糙度预测模型在给定的参数范围内能满足使用要求。 利用多目标线性规划法求解多目标优化模型的最优解，得出Xmin＝［320，4，10，3000］T。此时，Ra＝0.34 μm，RmR＝12.8 cm3／s。经试验验证，该理论解正确。