基于PR状态方程的天然气水合物生成温度计算

王承坤

(中海石油(中国)有限公司天津分公司，天津 300450)

1 理论部分

1.1 状态方程

PR方程由Ding-YU Peng和D.B.Robinson在1976年提出，广泛应用于烃类气体相态的计算，PR方程的一般形式为：

(1)

令A=aP/(RT)2，B=bP/RT，V=ZRT/P，则上式写成压缩因子 Z 表示的三次方程形式为：

Z3-(1-B)Z2+(A-3B2-2B)Z-(AB-B2-B3)=0

(2)

式中，b=0.0778RTc/Pc；a是温度的函数，a=acα。

ac=0.45724(RTc)2/Pc

(3)

m=0.37464+1.54226ω-0.26992ω2

(4)

式中，P为体系的压力，MPa；T为体系的温度，K；V为组分的摩尔体积，cm3/mol；Z为压缩因子；R为理想气体常数，8.314 J/(mol·K)；Pc为组分临界压力，MPa；Tc为组分临界临界温度，K；均可由资料查出；压缩因子Z值得求解时可用迭代法求解。

在计算混合流体热力学参数时，本文采用范德华混合规则：

(5)

(6)

式中，xi、xj为各组分的摩尔分数，kij为二元交互作用参数，本文kij数据取自文献[1]。

由PR方程计算逸度的公式为：

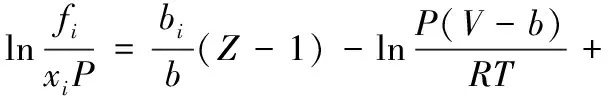
(7)

式中，fi为i组分逸度，xi为i组分摩尔分数。

1.2 相平衡计算

对于以单相存在的天然气系统，可直接用PR状态方程计算各组分热力学参数，对于系统为气液两相时，就要通过两相闪蒸计算各组分的热力学参数，本文采用郭天民等[2]介绍的方法，其步骤为：

(1)输入天然气组分和系统压力。

(2)用威尔逊公式赋予平衡常数K的初值：

Ki=Pci[5.373(1+ωi)(1-Tci/T)]/P

(4)当所有组分均满足循环收敛精度后，计算出达到气液平衡条件时各组分的逸度。

1.3 天然气水合物生成模型

Vander waals和Platteeuw在1959年提出了简单的天然气水合物生成模型[3]，认为对有水合物生成的体系，水在水合物相(H相)与在富水相(W相)中的化学位μ相等，即：

μH=μW

(8)

计算天然气水合物生成温度时，以完全空的水合物相的化学位为基础，分别计算出其与水合物相和富水相的化学位差，当ΔμH=ΔμW时，水在两相中的化学位亦相等。

1.3.1 水合物相的计算

根据Vander waals和Platteeuw的的理论，计算空水合物晶格和填充晶格相态的化学位差ΔμH为：

(9)

式中：θjm为m类孔隙被j组分分子所占据的分率；R是气体常数，取值为8.314 J/mol·K；T为体系温度，K;γm是m型孔穴的特性常数，与水合物结构相关，数值见文献[3]：

(10)

式中：fj(T,P)为j组分在气相中的逸度，由PR状态方程计算，kPa;Nc为形成水合物的天然气组分数；Cjm为j组分在m型孔穴中的朗缪尔气体吸附常数，1/kPa。

杜亚和、郭天民在1988年通过改进朗缪尔常数的计算方法，形成了Du-Guo88模型，该模型采用下式计算Cjm：

(11)

对于I型和II型水合物，公式中的常数Ajm、Bjm、Djm取值见文献[3]。

1.3.2 富水相的计算

Parrish和Prausnitz提出了Δuw的计算式，Holder等[4]改进后形成如下表达式:

(12)

式中，右边第一项表示标准态(T=273.15 K，P=0)下水的化学位偏差；后面三项分别表示温度、压力和浓度的校正；xw为富水液相中水的摩尔分率，由于天然气组分大多难容于水，xw取1。

(13)

(14)

2 计算步骤

下面给出在计算机上的实现步骤，若已知系统压力，求水合物形成温度时，利用VB语言编制程序，用Du-Guo88模型进行计算的流程如下：

(1)首先假设一种水合物结构类型；

(2)给定天然气干基组分及体系压力；

(3)对水合物生成温度赋初始值；

(4)进行相平衡计算，用PR状态方程计算气相fj；

(5)按式(11)计算朗缪尔吸附常数Cjm；

(6)按式(9)计算ΔμH；

(7)按式(12)计算ΔμW；

(8)计算|Δμw-μH|<10-4是否成立，如果成立就显示计算所得的温度值，否则调整温度值，重新进行步骤(4)～(9)，直到满足精度要求则停止；

(9)指定另一种水合物类型，计算生成温度，将两次所得温度值进行比较，其中较高者即为水合物的生成温度。

3 实例计算

为验证计算的准确性，利用Visual Basic程序将上述提到的方法涉及的复杂计算公式软件化，实现快速计算。

图1 软件运行界面Fig.1 Software running interface

本文采取文献中4组天然气体系对模型进行验证：

No.1，No.2天然气水合物数据来自文献[5]，数据取自广州天然气水合物研究中心相平衡研究所；No.3，No.4数据来自文献[6]，分别为北海某气田和平湖气田的天然气水合物数据。

表1 计算结果相对误差Table 1 Relative error of results

续表1

通过对本文提到的计算方法进行编程，将上述4种天然气组分进行生成温度计算，与文献中的值进行比较，考察结果如表1所示。

平均相对误差计算公式：

式中：Np为水合物数据点的数目；Texp，Tcal分别表示文献中水合物形成温度值和本文方法计算的水合物形成温度。

从以上数据可以看出，采用本文方法计算水合物生成温度，所得数据与文献值较为吻合，平均相对误差小于0.63%。

4 结 论

(1)本文在天然气水合物生成温度计算时考虑流体相态变化，采用PR状态方程计算相平衡来描述流体相态变化，更符合天然气在集采过程中发生相变的实际情况，避免了计算偏差。

(2)采用本文的方法进行天然气水合物生成温度计算所得数据与文献值相比平均误差较小，证明了本文计算方法是可行的，完全可以满足工程应用。

(3)利用计算机编程将本文提到的复杂计算方法软件化，可实现快速计算，在现场应用上取得了良好效果。