参考作物蒸发蒸腾量计算方法在甘肃省不同区域的适用性分析
郑健,鲍婷婷,杨赟,陈娅
▪作物水肥高效利用▪
参考作物蒸发蒸腾量计算方法在甘肃省不同区域的适用性分析
郑健1,2,3,鲍婷婷1,2,杨赟4,陈娅1,2
(1.兰州理工大学 能源与动力工程学院,兰州 730050;2.甘肃省生物质能与太阳能互补供能系统重点实验室,兰州 730050;3.西北低碳城镇支撑技术协同创新中心,兰州 730050;4.临夏回族自治州水利科学研究院,甘肃 临夏 731100)
【目的】分析参考作物蒸发蒸腾量计算方法在甘肃省不同区域的适用性。【方法】把甘肃省划分为4个区域(I区,河西干旱区;Ⅱ区,陇中北部半干旱区;Ⅲ区,陇中南部半湿润区;Ⅳ区,陇南-甘南湿润区),在此基础上,采用甘肃省26个国家气象站点1980—2019的气象资料,并以FAO-56 Penman Monteith(P-M)法作为计算0的标准方法,同时选用Hargreaves-Samani(Har)法、FAO-24 Penman(24PM)法、FAO 1948 Penman(48PM)法、Makkink(Mak)法、Priestley-Taylor(PT)法5种简化方法计算甘肃省各个站点的0,对5种简化方法在4个分区的适用性进行分析。【结果】5种简化方法在甘肃省不同分区的计算精度存在明显差异,Har法和Mak法分别与P-M法的相关系数更接近1,拟合曲线的拟合程度更好,表现出了较高的计算精度,适用性较好,但Har法在高海拔地区计算精度明显下降;48PM法和24PM法比P-M法计算结果偏大,计算精度居中;PT法计算精度整体较低。不同计算方法在各区的适用性顺序为,I区:Mak法>Har法>48PM法>24PM法>PT法;Ⅱ区、Ⅲ区、Ⅳ区:Har法>Mak法>48PM法>24PM法>PT法。【结论】当气象资料出现缺失时,推荐在I区选用Mak法,在Ⅱ区、Ⅲ区和Ⅳ区选用Har法。
参考作物蒸发蒸腾量(0);简化计算方法;适用性分析;甘肃省
0 引言
【研究意义】作物需水量的准确计算是发展农业高效节水的关键,尤其在干旱缺水的中国西北地区,对作物需水量进行生产管理变得尤为重要,而参考作物蒸发蒸腾量(0)就是估算作物需水量的一个重要参数。0主要受气象因子的影响,适用局限性小,是有效利用、合理分配水资源,优化区域种植结构和制定区域农业节水灌溉的一个重要依据[1]。
【研究进展】1998年FAO推荐的FAO-56 Penman Monteith(P-M)法是一种能精确计算0的标准方法,在相关领域比较成熟,但同时所需要的气象资料也比较全面[2-3]。针对上述实际问题,国内外众多学者对0的不同计算方法进行了大量的研究,提出了受温度因素影响较大的Hargreaves-Samani(Har)法[4];受辐射因素影响较大的Makkink(Mak)法[5]、Priestley-Taylor(PT)法[6];还有FAO 1948 Penman(48PM)法[7]、FAO-24 Penman(24PM)法[8]等多种简化计算方法。国外学者Fotios等[9]、Tabaari[10]、Valipour[11]和国内学者李晨等[12]、王延珺等[13]、杨浩亮等[14]在不同研究区域应用简化的0方法计算分析时,均发现不同研究区域适宜的简化计算方法存在差异,利用简化方法计算0虽然对某些缺少气象资料地区非常有利,但由于地形地势、自然环境等条件的不同,同一方法在不同地区的计算精度仍然存在较大的差异性。
【切入点】甘肃省地处我国西北内陆地区,东西横跨1 600多km,地理位置独特,气候类型复杂多样,因此不同分区0的计算数值差异性比较大,但目前对不同区域0计算方法适宜性的研究还较少。
【拟解决的关键性问题】基于此,本文在郑健等[1]把甘肃省划分为河西干旱区(I区)、陇中北部半干旱区(Ⅱ区)、陇中南部半湿润区(Ⅲ区)、陇南-甘南湿润区(Ⅳ区)4个区域的基础上(具体分区依据见图1和参考文献[3]),利用Har法、24PM法、PT法、48PM法、Mak法5种简化方法和P-M法分别计算甘肃省各分区的0值,并以P-M法为标准对其他5种简化方法计算结果的适用性和相关性进行分析。获得甘肃省各分区0计算精度最高的方法,以期为甘肃省农田节约用水和水资源优化调度提供有力参考。
1 材料与方法
1.1 研究区域概况及数据来源
甘肃省地域辽阔,地理位置特殊,东西南北分别与陕西、新疆和蒙古人民共和国、四川、内蒙古和宁夏相接。是一个跨越多种地形与地貌的狭长省份,这就使甘肃省具有多种多样的地势地貌与气候类型[15]。图1为甘肃省26个国家级气象站点和各分区分布图。
气象数据来源于中国气象科学数据共享服务网,选用全省气象观测数据比较完备的气象站点,并对各个站点内缺测数据科学地进行插补,由于本文所选用的气象站点数据比较完备,不存在较长序列数据的缺测,因此本文只需对较短序列缺测数据进行插补,插补方法如下[16]:①若缺测序列≤5 d,则采用线性插值方法插补;②5 d<缺测序列≤30 d,则用同一日值的多年平均值补齐。最后整理得到甘肃省26个国家级气象站点1980—2019年的气象数据,包括降水量、气温(平均气温mean、日最高气温max、日最低温min)、日照时间、平均相对湿度、日平均风速和海拔高度等逐日气象资料。
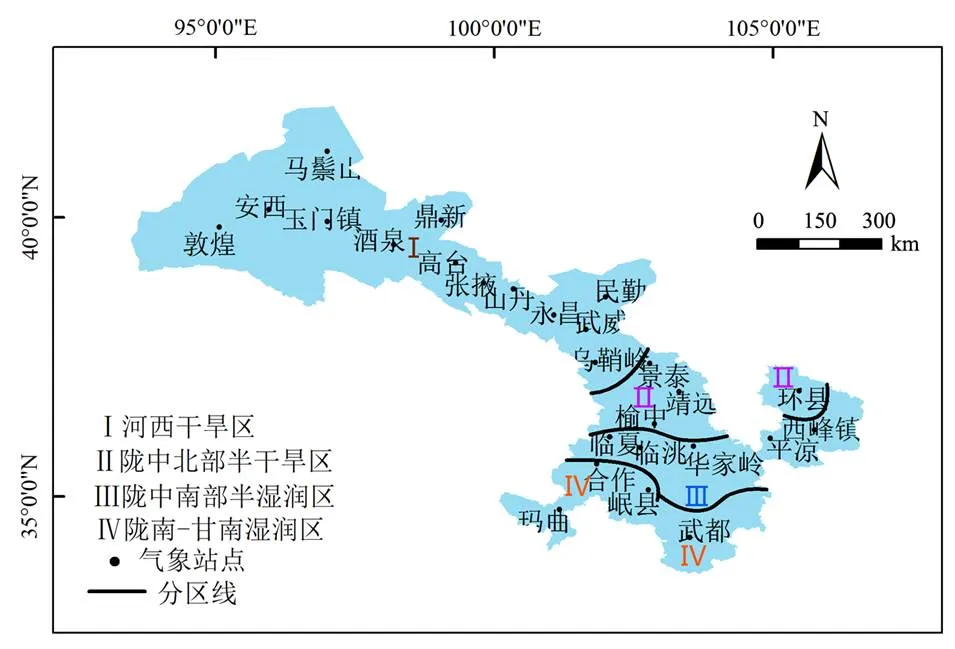
图1 甘肃省气象站点和分区分布
1.2 研究方法
1.2.10计算方法
本文所选用的6种计算方法已在相关领域得到广泛的运用,计算结果可靠有效,其具体计算式见表1。

表1 ET0计算方法
注 表中∆、、、s、a、s等参数可参考文献[24]。
1.2.2 数据分析方法
反距离权重空间插值法(Inverse Distance Weighted,简称IDW)是一种比较圆滑、确切的内插值法,本文选用某区域内未采样点周围观测点的数据对该点的数据进行插值,从而获得高精度未采样点数据的估计值[25]。评价指标选用平均相对误差。利用ArcGIS 10.4软件进行空间插值,Matlab R2012b软件分析评价指标。平均相对误差[26]()和变异系数[27]()计算式为:

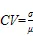
式中:M为各简化方法的0计算值;E为标准方法P-M法的0计算值;为各简化方法的0计算值的标准差;为各简化方法的0平均值。
2 结果与分析
2.1 不同方法计算ET0年平均值的比较
采用P-M法和Har法、24PM法、48PM法、Mak法、PT法5种简化方法分别计算逐年0,详见图2。由图2可知,6种计算方法的年0平均值趋势线基本一致,24PM法、48PM法、PT法、Mak法计算的0最小值与P-M法一样都出现在1989年,计算值分别为1 202.952、1 105.065、1 549.743、826.667、931.402 mm/a;24PM法、48PM法计算的0最大值与P-M法一样,都出现在2016年,计算值分别为1 281.174、1 420.383 mm/a。24PM法、48PM法和PT法年平均计算结果相较P-M法明显偏大,Har法和Mak法年平均计算结果相较P-M法明显偏小。PT法标准差相较于其他各简化方法最大,为53.429 mm/a,表明计算结果较不稳定,其余各简化方法标准差小于43.369 mm/a,表明计算结果相对稳定。通过上述分析可知5种简化方法与P-M法变化趋势整体上基本相同,但数值差异明显,尤其是PT法年均0值比P-M法年均0值增大了66.39%,且计算结果最不稳定,说明2种计算方法之间差异最大;Har法计算的年均值与P-M法比较接近,略小于P-M法,说明2种方法之间差异最小。
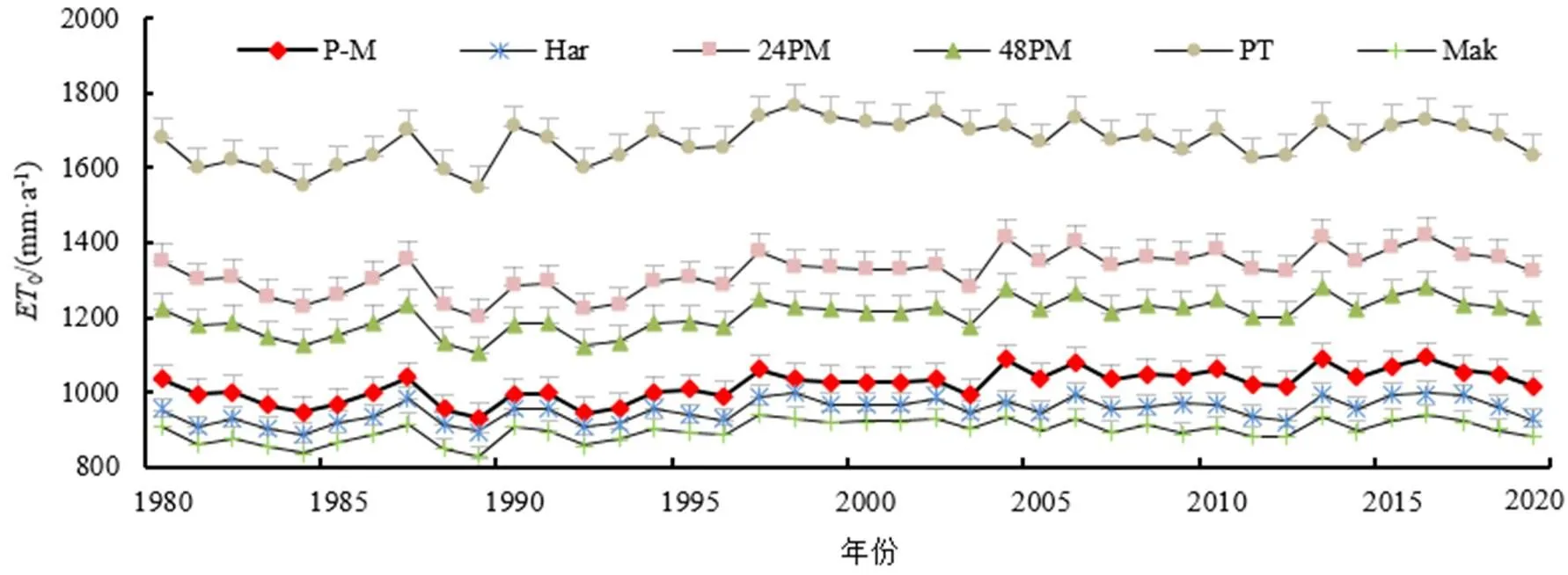
图2 甘肃省ET0标准算法(P-M)与各简化算法年平均值对比
2.2 不同方法计算ET0月平均值的比较
采用P-M法和Har法、24PM法、48PM法、Mak法、PT法5种简化方法分别计算逐月0,并求出各月的平均值。图3为P-M法与其他5种简化方法的0月平均值对比图,图4为P-M法与其他5种简化方法的0月平均相对误差图。由图3可以看出,6种方法的计算结果在年内的变化趋势基本相同,都呈开口向下的抛物线形式。在I区、Ⅲ区,除24PM法外,其余简化方法与P-M法计算的0最大值都出现在7月,而24PM法在6月就已经出现了最大值;Ⅱ区,除Mak法外,其余简化方法与P-M法计算的0最大值也出现在7月,而Mak法在5月已经出现了最大值;Ⅳ区,与P-M法一样0最大值出现在7月的有Har法、24PM法和48PM法,但Mak法和PT法在8月出现了最大值;4个分区1、12月0值都比较小。进一步分析图4可知,4个分区各简化方法与P-M法的相对误差变化趋势基本一致,48 PM法和Mak法在各分区的变化趋势和24PM法在I区、Ⅱ区和Ⅲ区的变化趋势一样,都是先减少后增大,Har法和PT法在4个分区的变化趋势基本上都是先增大后减小。在I区,相对误差最接近0的是Mak法,6—7月0值小于P-M法,其他月份0值大于P-M法,相对误差在-7.24%~11.84%之间;在Ⅱ区、Ⅲ区和Ⅳ区相对误差最接近0的都是Har法,Ⅱ区,4—10月0值大于P-M法,其他月份0值小于P-M法,相对误差在-26.00%~8.98%之间;Ⅲ区,7—9月0值大于P-M法,其他月份0值小于P-M法,相对误差在-19.88%~2.74%之间;Ⅳ区,4—10月0值大于P-M法,其他月份0值小于P-M法,相对误差在-11.52%~10.05%之间。4个分区内表现居中的都是24PM法和48PM法,0值均大于P-M法,24PM法在4个分区的相对误差分别在27.68%~43.09%、22.09%~32.53%、22.36%~45.11%、16.61%~21.48%之间;48PM法在4个分区的相对误差分别在12.96%~27.47%、16.72%~25.74%、14.03%~33.23%、14.79%~23.62%之间。4个分区内表现最不好的都是PT法,相对误差在23.73%~98.43%之间。因此,5种简化方法在I区适用性最好的是Mak法,在Ⅱ区、Ⅲ区和Ⅳ适用性最好的是Har法;24PM法和48PM法在各区适用性居中,而在各区适用性最不好的都是PT法。
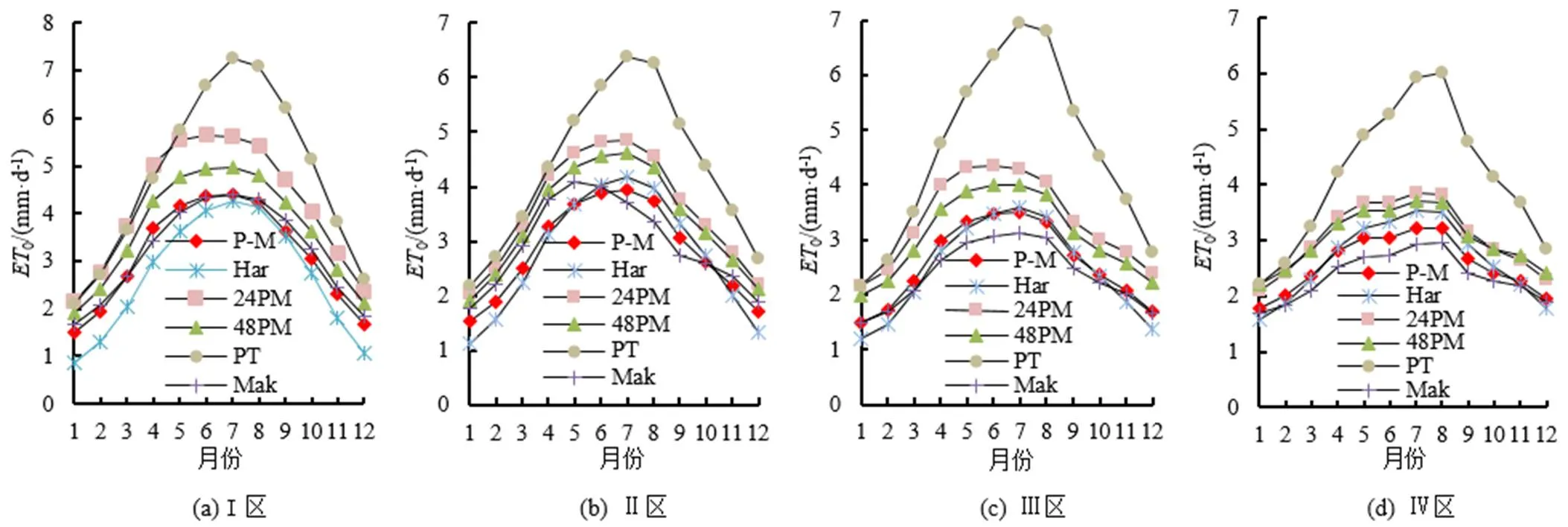
图3 甘肃省不同区域ET0标准算法(P-M)与各简化算法月平均值对比

图4 甘肃省不同区域ET0标准算法(P-M)与各简化算法月平均相对误差对比
2.3 5种简化方法计算精度空间分析
应用ArcGIS 10.4软件对26个气象站点5种简化算法与P-M法0年均值、0日均值变异系数、0日均值平均相对误差进行反距离权重插值,得到P-M法与其他5种0简化算法在甘肃省的0年均值空间分布图(图5)、0日均值变异系数空间分布图(图6)、0日均值平均相对误差空间分布图(图7),对各分区0的稳定性和误差分布进行分析。由图5可知,P-M法、24PM法、48PM法和Mak法的0计算值在甘肃省的总体特征为自西北向东南逐渐减小,即依次为I区、Ⅱ区、Ⅲ区、Ⅳ区,0最大值分别为1 313.24、1 821.46、1 496.61、1 016.84 mm/a,最小值分别为866.07、1 083.67、1 022.86、776.28 mm/a;在甘肃省的马鬃山、乌鞘岭和华家岭Har法的0计算值相对较小,分别为875.562、604.99、662.89 mm/a;PT法的0计算值在甘肃省整体偏大,最大值为2 576.00 mm/a,最小值为2 064.51 mm/a。由图6可知,Mak法在I区的变异系数相对较小,在15.25%~22.68%之间,Har法在Ⅱ区、Ⅲ区、Ⅳ区的变异系数相对较小,在15.75%~28.81%之间,表明I区Mak法、Ⅱ区、Ⅲ区、Ⅳ区Har法计算结果比较稳定;24PM法和48PM法的变异系数在甘肃省的玛曲较小,分别为10.94%、11.70%,而在甘肃省其余各地24PM法和48PM法的变异系数都比较大,表明计算结果不稳定;PT法的变异系数在4个分区都比较大,在31.24%~57.73%之间,表明计算结果极不稳定。由图7可知,与P-M法相比,Har法除在马鬃山、乌鞘岭和华家岭等地区相对误差稍大外,在甘肃省大部分地区相对误差都比较小,尤其在Ⅱ区和Ⅳ区,分别在8.93%~15.95%之间和5.41%~7.49%之间,表明计算结果良好,采用Har法计算0时主要考虑气温因素的影响,马鬃山、乌鞘岭和华家岭受地理位置等多种因素的影响,导致温差较大,这就使其利用Har法计算的结果相对误差偏大;48PM法除在乌鞘岭、华家岭和靖远等地区相对误差比较大外,其余地区整体相对误差都比较小,在8.41%~28.44%之间,尤其Ⅳ区的计算结果比较稳定,在18.29%~18.65%之间,这可能是48PM法和P-M法采用了相同的空气动力学项;24PM法和PT法在整个甘肃省的相对误差都比较大,分别在14.16%~44.69%和17.64%~93.32%之间,尤其在I区,24PM法的相对误差更大,在31.13%~44.69%之间,这可能是该方法中风速函数的原因,Ⅱ区、Ⅲ区和Ⅳ区PT法的相对误差偏大,处于59.69%~93.32%之间,这可能是PT法只考虑了太阳辐射这一影响因素的原因。Mak法相较于24PM法和PT法表现较好,特别是在I区和Ⅳ区,在2.41%~24.58 %之间。由以上分析可知,Har法在整个甘肃误差普遍较小,表明计算结果良好,而PT法在整个甘肃误差都是最大的,表明适用性最差。
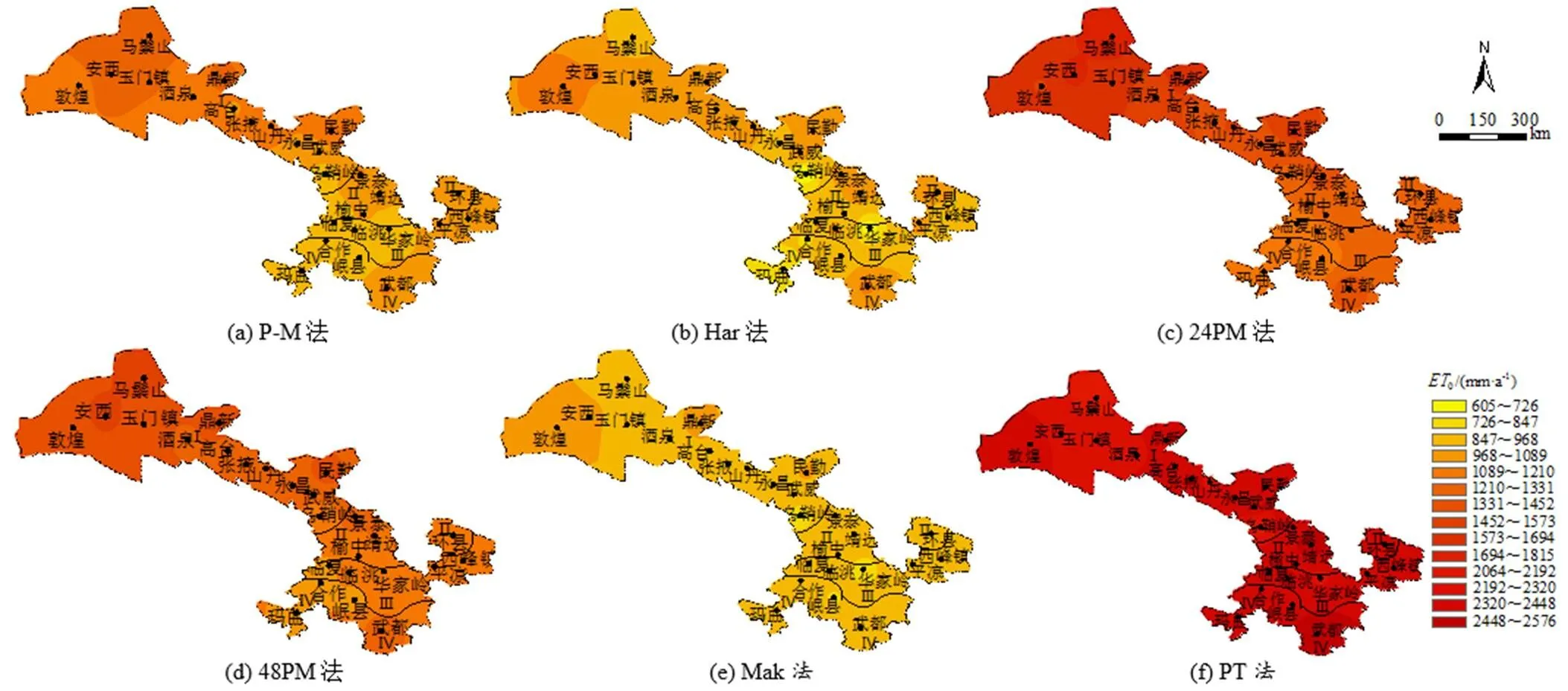
图5 1980—2019年甘肃省ET0空间分布

图6 甘肃省5种简化算法ET0变异系数空间分布

图7 甘肃省ET0标准算法结果(P-M)与5种简化算法的相对误差空间分布
2.4 ET0不同计算方法结果偏差分析
将P-M法计算的1980—2019年的逐月0作为标准结果,其他5种简化的方法分别与该方法进行拟合,得到拟合曲线趋势线斜率和相关系数2,如表2所示。I区,Har法、24PM法、48PM法、Mak法与P-M法的曲线拟合程度都比较好,决定系数2在0.931~0.997之间,但与P-M法拟合曲线的趋势线斜率最接近1的是Mak法,为0.866,Har法、24PM法、48PM法与P-M法拟合曲线的趋势线斜率偏大,处于1.217~1.362之间,表明计算结果比标准法的计算结果偏大,因此Mak法在I区的计算精度相对最高;Ⅱ区、Ⅲ区、Ⅳ区,Har法、24PM法、48PM法、Mak法与P-M法曲线拟合程度同样都比较好,决定系数2在0.937~0.998之间,但24PM法、48PM法与P-M法拟合曲线的趋势线斜率偏大,处于1.196~1.383之间,表明计算结果比标准法计算结果偏大,Mak法与P-M法拟合曲线的趋势线斜率偏小,处于0.737~0.836之间,表明计算结果比标准法计算结果偏小,与P-M法拟合曲线的趋势线斜率最接近1的是Har法,表明计算精度相对最高;PT法与P-M法曲线拟合程度在各区都最差,决定系数2处于0.898~0.905之间,与P-M法拟合曲线的趋势线斜率在各区也最大,处于1.557~2.298之间,表明计算结果偏大。因此,Mak法在I区适用性相对更好,Har法在Ⅱ区、Ⅲ区、Ⅳ区适用性相对更好。

表2 甘肃省各分区不同简化方法ET0计算结果与标准法(P-M)法拟合结果
注 表中为趋势线斜率,2为相关系数。
3 讨论
国内外学者对参考作物蒸发蒸腾量在不同区域的适用性已经做了大量的研究,发现不同区域最适宜的0计算方法各不相同,李晨等[12]在用6种0计算方法对四川省参考作物蒸发蒸腾量的适用性研究中发现,PT法计算结果更接近P-M法,在四川省计算精度最高,48PM计算精度最差;孙庆宇等[2]用6种0计算方法对海河流域参考作物蒸发蒸腾量的适用性研究中发现,24PM法计算结果更接近P-M法,计算精度普遍较高。甘肃省南北纬度跨越了10°,且河西干旱区纬度高于甘肃省其他地区,平均海拔在3 000 m左右,且昼夜温差大,温度法中的Har法对气温变化比较敏感,受到了极不稳定的气温这一影响因素[8],这可能是Har法计算结果在甘肃省I区的计算精度较差的原因;PT法在各区计算精度都最差,其主要原因初步分析是PT法中的被当作了常数,其实∂在不同研究背景下的取值各不相同,只是许多学者把它当作了一个经验值,这就使得用PT法计算的结果出现了较大的误差;Mak法是在不考虑土壤热通量的前提下把PT法计算式中的净辐射换成了太阳辐射总结出的式子,但本文中Mak法式中所用到的修正系数为0.61,实际上就是净辐射与太阳辐射的比值,这个比值并不是固定不变的,它是随着季节而变化的,这是Mak法在甘肃省Ⅱ区、Ⅲ区和Ⅳ区产生误差的主要原因,同时PT法中的系数∂是利用海面和湿润陆面的资料得出的经验值,而Mak法中的系数0.16是净辐射与太阳辐射的比值,且由于PT法考虑了土壤热通量这一因素的影响,而Mak法不考虑,这可能就是PT法在甘肃省的模拟效果最差,而Mak法的模拟效果相对较好的原因[28];综合类法中的48PM法和24PM法计算结果在空间上随地势自东南向西北逐渐增大,受地形影响明显,这是因为48PM法和24PM法是把P-M法中的空气动力学项用修正后的日照时间,日平均风速来代替,使其无法克服地形等因素的影响,导致最后计算结果普遍偏大[12]。范文波等[4]在对玛纳斯河流域参考作物蒸发蒸腾量的研究中发现,对Har法公式中的常数采用贝叶斯方法进行修正后,得出修正后的Har法明显要比未修正的Har法计算精度高。因此,根据研究区域的实际情况对各简化方法进行修正改进,在一定程度上可以提高0的计算精度。
本研究涉及的区域跨度大,地形地貌,海拔等条件也相差比较大,为了减少误差,所选取的0计算方法是众多学者在研究中被证明比较可靠、有参考价值的方法,但计算0的其他简化方法还有很多,本文并未全部引用,且在研究甘肃省参考作物的蒸发蒸腾量时对0计算公式的修正改进方面还未涉及,所以在选取0计算方法上还存在一定的局限性;同时本文各分区所选取的气象站点相对比较少,可能对计算结果有一定的影响。上述所存在的问题与不足本团队将在后续工作中继续探讨。
4 结论
1)各分区P-M法和各简化方法的0值随年际的变化都呈上升趋势,各分区内24PM法、48PM法和PT法的0平均值显著大于P-M法,而Har法、Mak法与P-M法的0平均值没有显著差异。
2)各分区计算精度普遍较高的是Har法和Mak法,体现出了较好的适用性;48PM法和24PM法计算结果尤其是在Ⅲ区和Ⅳ区偏大;PT法计算结果在全省都偏大,不建议采用。
3)各分区简化方法与P-M法计算结果拟合程度最不好的是PT法,其余简化方法与P-M法计算结果拟合程度相对来说比较好。
4)各简化方法在I区适用性顺序为:Mak法>Har法>48PM法>24PM法>PT法;在Ⅱ区、Ⅲ区和Ⅳ区的适用性顺序为:Har法>Mak法>48PM法>24PM法>PT法;推荐在I区选用Mak法,在Ⅱ区、Ⅲ区和Ⅳ区选用Har法。
[1] 郑健, 马静, 王燕, 等. 基于气候分区的甘肃省参考作物蒸发蒸腾量时空分布特征[J]. 水资源与水工程学报, 2020, 31(1): 240-247.
ZHENG Jian, MA Jing, WANG Yan, et al. Temporal-spatial distribution characteristics of reference crop evapotranspiration in Gansu based on climatic zones[J]. Journal of Water Resources and Water Engineering, 2020, 31(1): 240-247.
[2] 孙庆宇, 佟玲, 张宝忠, 等. 参考作物蒸发蒸腾量计算方法在海河流域的适用性[J]. 农业工程学报, 2010, 26(11): 68-72.
SUN Qingyu, TONG Ling, ZHANG Baozhong, et al. Comparison of methods for calculating reference crop evapotranspiration in Haihe River basin of China[J]. Transactions of the Chinese Society of Agricultural Engineering, 2010, 26(11): 68-72.
[3] 马静. 基于气候分区的甘肃省参考作物蒸发蒸腾量分析与预测[D]. 兰州: 兰州理工大学, 2021.
MA Jing. Analysis and prediction of reference crop evapotranspiration in Gansu Province Based on climatic regionalization[D]. Lanzhou: Lanzhou University of Technology, 2021.
[4] 范文波, 吴普特, 韩志全, 等. 玛纳斯河流域0影响因子分析及对Hargreaves法的修正[J]. 农业工程学报, 2012, 28(8): 19-24.
FAN Wenbo, WU Pute, HAN Zhiquan, et al. Influencing factors analysis of reference crop evapotranspiration and modification of Hargreaves method in Manas river basin[J]. Transactions of the Chinese Society of Agricultural Engineering, 2012, 28(8): 19-24.
[5] 李志. 参考作物蒸散简易估算方法在黄土高原的适用性[J]. 农业工程学报, 2012, 28(6): 106-111.
LI Zhi. Applicability of simple estimating method for reference crop evapotranspiration in Loess Plateau[J]. Transactions of the Chinese Society of Agricultural Engineering, 2012, 28(6): 106-111.
[6] PRIESTLEY C H B, TAYLOR R J. On the assessment of surface heat flux and evaporation using large scale parameters[J]. Monthly Weather Review, 1972, 100(2): 81-92.
[7] PATHAK HILOR, LI CHUNY, WASSMANN REINER. Greenhouse gas emissions from Indian rice fields: calibration and upscaling using the DNDC model[J]. Biogeosciences, 2005, 2(2): 113-123.
[8] 高蓉, 吴雷, 顾世祥, 等. 云南立体气候条件下参考作物腾发量计算方法的适用性研究[J]. 灌溉排水学报, 2020, 39(7): 91-99.
GAO Rong, WU Lei, GU Shixiang, et al. Sduty on adaptation of reference crop evapotranspiration calculation methods under stereo climatic conditions in Yunnan Province[J]. Journal of Irrigation and Drainage, 2020, 39(7): 91-99.
[9] FOTIOS XYSTRAKIS P D, MATZARAKIS ANDRES. Evaluation of 13 empirical reference potential evapotranspiration equations on the island of crete in southern greece[J]. Canadian Metallurgical Quarterly, 2011, 137(4): 211-222.
[10] TABAARI HOSSEIN. Evaluation of reference crop evapotranspiration equations in various climates[J]. Water Resources Management, 2010, 24(10): 2 311-2 337.
[11] VALIPOUR MOHAMMAD. Use of average data of 181 synoptic stations for estimation of reference crop evapotranspiration by temperature-based methods[J]. Water Resources Management, 2014, 28(12): 4 237-4 255.
[12] 李晨, 崔宁博, 冯禹, 等. 四川省不同区域参考作物蒸散量计算方法的适用性评价[J]. 农业工程学报, 2016, 32(4): 127-134.
LI Chen, CUI Ningbo, FENG Yu, et al. Adaptation evaluation for reference evapotranspiration methods in different regions of Sichuan[J]. Transactions of the Chinese Society of Agricultural Engineering, 2016, 32(4): 127-134.
[13] 王延珺, 张海涛, 杜军凯, 等. 简化参考作物蒸发蒸腾量计算方法在都江堰灌区的应用[J]. 水电能源科学, 2021, 39(11): 166-169, 47.
WANG Yanjun, ZHANG Haitao, DU Junkai, et al. Study on applicability of simplified calculation method of reference crop evapotranspiration in Dujiangyan area[J]. Water Resources and Power, 2021, 39(11): 166-169, 47.
[14] 杨浩亮, 张文贤, 次吉拉姆, 等. 不同0计算方法在西藏林芝的适用性研究[J]. 高原农业, 2019, 3(5): 544-550.
YANG Haoliang, ZHANG Wenxian, CIJI lamu, et al. Applicability of different0calculation methods in Linzhi, Tibet[J]. Journal of Plateau Agriculture, 2019, 3(5): 544-550.
[15] 温克刚, 董安祥. 中国气象灾害大典·甘肃卷[M]. 北京: 气象出版社, 2005.
WEN Kegang, DONG Anxiang.China Meteorological Disaster ceremony·Gansu volume[M]. Beijing: China Meteorological Press, 2005.
[16] 李亮, PICH LINVOLAK, 蔡焕杰. 基于标准化降水蒸散指数的甘肃省干旱时空特征分析[J]. 干旱地区农业研究, 2019, 37(3): 256-266.
LI Liang, PICH LINVOLAK, CAI Huanjie. Analysis of spatio-temporal distribution of drought characteristics based onin Gansu Province[J]. Agricultural Research in the Arid Areas, 2019, 37(3): 256-266.
[17] PERERA KUSHAN C, WESTER ANDRE W, NAWARATHNA BANDARA, et al. Comparison of hourly and daily reference crop evapotranspiration equations across seasons and climate zones in Australia[J]. Agricultural Water Management, 2015, 148(31): 84-96.
[18] HARGREAVES GEORGR H, SAMANI ZOHRAB A. Reference crop evapotranspiration from temperature[J]. Applied Engineering in Agriculture, 1985, 1(2): 96-99.
[19] 尹春艳, 陈小兵, 刘虎, 等. 黄河三角洲参考作物腾发量计算方法适宜性研究[J]. 灌溉排水学报, 2017, 36(6): 36-41.
YIN Chunyan, CHEN Xiaobing, LIU Hu, et al. Comparison of different methods for calculating evapotranspiration of crops in the Yellow River Delta[J].Journal of Irrigation and Drainage, 2017, 36(6): 36-41.
[20] 彭世彰, 徐俊增. 参考作物蒸发蒸腾量计算方法的应用比较[J]. 灌溉排水学报, 2004, 23(6): 5-9.
PENG Shizhang, XU Junzeng. Comparison of reference crop evapotranspiration computing methods[J]. Journal of Irrigation and Drainage, 2004, 23(6): 5-9.
[21] 高凌智, 李彬, 史海滨, 等. 鄂尔多斯高原不同0计算方法的适用性比较: 以鄂托克旗为例[J]. 北方农业学报, 2019, 47(1): 114-119.
GAO Lingzhi, LI Bin, SHI Haibin, et al. Comparison of the applicability of0determined with different calculation methods in the Ordos Plateau: Taking the Etuoke Banner as an example[J]. Journal of Northern Agriculture, 2019, 47(1): 114-119.
[22] 张育斌, 胡杨, 朱新国, 等. 宁波地区参考作物蒸散量计算模型研究[J]. 农业与技术, 2017, 37(3): 1-4.
ZHANG Yubin, HU Yang, ZHU Xinguo, et al.Study on calculation model of reference crop evapotranspiration in Ningbo[J].Agriculture and Technology, 2017, 37(3): 1-4.
[23] MAKKINK G F. Testing the Penman Formula by means of lysimeters[J]. Jinst Water Engineers, 1957, 11(3): 277-288.
[24] ALLEN RICHARD G. Crop Evapotranspiration-Guidelines for computing crop water requirements[M]. Rome: FAO Irrigation and Drainage Publications No.56, 1998.
[25] 樊子德, 李佳霖, 邓敏. 顾及多因素影响的自适应反距离加权插值方法[J]. 武汉大学学报(信息科学版), 2016, 41(6): 842-847.
FAN Zide, LI Jialin, DENG Min. An adaptive inverse-distance weighting spatial interpolation method with the consideration of multiple factors[J]. Geomatics and Information Science of Wuhan University, 2016, 41(6): 842-847.
[26] 强小嫚, 蔡焕杰, 孙景生, 等. 陕西关中地区0计算公式的适用性评价[J]. 农业工程学报, 2012, 28(20): 121-127.
QIANG Xiaoman, CAI Huanjie, SUN Jingsheng, et al. Adaptability evaluation for reference evapotranspiration (0) formulas in Guanzhong Region of Shaanxi[J]. Transactions of the Chinese Society of Agricultural Engineering, 2012, 28(20): 121-127.
[27] LORENZO CARLOS JOSE, YABOR LOURDES, MEDINA NORMA, et al. Coefficient of variation can identify the most important effects of experimental treatments[J]. Notulae Botanicae Horti Agrobotanici Cluj-Napoca, 2015, 43(1): 83-98.
[28] 李玉霖, 崔建垣, 张铜会. 参考作物蒸散量计算方法的比较研究[J]. 中国沙漠, 2002, 22(4): 372-376.
LI Yulin, CUI Jianyuan, ZHANG Tonghui. Comparative study on calculation methods of reference evapotranspiration[J]. Journal of Desert Research, 2002, 22(4): 372-376.
Reference Evapotranspiration in Gansu Province Calculated Using Different Methods
ZHENG Jian1,2,3, BAO Tingting1,2, YANG Yun4, CHEN Ya1,2
(1. College of Energy and Power Engineering, Lanzhou University of Technology, Lanzhou 730050, China; 2. Key Laboratory of the System of Biomass Energy and Solar Energy Complementary Energy Supply System in Gansu, Lanzhou 730050, China; 3. Collaborative Innovation Center of Key Technology for Northwest Low Carbon Urbanization, Lanzhou 730050, China; 4. Water Conservancy Research Institute of Linxia Hui Autonomous Prefecture, Linxia 731100, China)
【Objective】Reference evapotranspiration (0) measures the potential water loss from soils in terrestrial systems. It varies with a multitude of factors and can be calculated by different methods. In this paper, we compared0calculated by five methods for regions with incomplete meteorological data across Gansu province in northwestern China. 【Method】We divided the province into four regions: arid area in Hexi (Region I), semi-arid area in northern Longzhong (Region II),semi-humid area in southern Longzhong (Region III), and humid area in Longnan and Gannan (Region IV).The reference evapotranspiration in each region was calculated using the Hargreaves-Samani (Har), the FAO-24 Penman (24PM), the FAO 1948 Penman (48PM), the Makkink (Mak), and the Priestley Taylor (PT) methods, respectively. For each method, we calculated the daily0based on data measured from 1980 to 2019 from 26 meteorological stations across the province. The accuracy and robustness of each method for each region was tested against that estimated using the FAO-56 penman Monteith (P-M) method. 【Result】0calculated from different methods varied, though the variation depended on region. The results calculated from the Har and Mak methods were correlated with that from the P-M method with the correlation coefficients close to unity, despite that the Har method was less accurate for high altitude regions. The results estimated by the 48PM and 24PM methods were both greater than the0calculated by P-M method. The accuracy of the five simplified methods for estimating0was ranked in the order of Mak > Har >48PM > 24PM > PT for Region I, and Har >Mak> 48PM > 24PM >PT for other three regions.【Conclusion】For regions that are lack of meteorological data, the Mak method was the best alternative for estimating0in Region I, while the Har method worked better for other regions in Gansu province.
reference crop evapotranspiration(0); calculation methods; applicability analysis; Gansu Province
郑健, 鲍婷婷, 杨赟, 等. 参考作物蒸发蒸腾量计算方法在甘肃省不同区域的适用性分析[J]. 灌溉排水学报, 2022, 41(10): 1-9.
ZHENG Jian, BAO Tingting, YANG Yun, et al. Reference Evapotranspiration in Gansu Province Calculated Using Different Methods[J]. Journal of Irrigation and Drainage, 2022, 41(10): 1-9.
S161.4
A
10.13522/j.cnki.ggps.2022183
1672 - 3317(2022)10 - 0001 - 09
2022-04-07
国家自然科学基金项目(51969012);甘肃省教育厅产业支撑计划项目(2021CYZC-27,2021CYZC-33);兰州理工大学红柳一流学科建设项目(0807J1)
郑健(1981-),男,甘肃会宁人。教授,博士生导师,博士,主要从事水资源高效利用与转化方面的研究。E-mail: zhj16822@126.com
责任编辑:白芳芳

