r 型网格自适应在间断Galerkin 有限元激波捕捉中的应用

龚小权 吴晓军 唐静 李明 张健

(中国空气动力研究与发展中心 计算空气动力研究所, 绵阳 621000)

间断Galerkin(discontinuous Galerkin,DG)有限元[1-2]方法作为一种适用于非结构网格的高精度方法,具有计算精度高,计算模板紧致,适合处理复杂外形及边界、初值问题,并行能力强,自适应计算方便等优点。

与其他高精度格式类似,DG 方法在模拟包含强间断流场时存在收敛性和鲁棒性差的问题。目前,大部分学者通过添加人工黏性[3-4]或限制器[5-6]来抑制激波附近的震荡。 人工黏性方法作为一种先验方法,在控制方程中添加代表黏性的二阶导数项,该项数值与计算网格、模拟问题相关,具有一定经验性,其对数值解的干扰没有统一的评估标准。 限制器作为一种后验方法,通过限制或重构多项式高阶自由度抑制数值震荡,其存在残差收敛滞止、结果收敛性差的问题。 目前,DG 方法的激波捕捉技术已成为其发展的瓶颈之一,国内外在限制器方面开展了大量研究,包括Barth-Jespersen 限制器[7]、Venkatakrishnan[8]限制器,以及Shu 等[9]按照WENO 重构思想在三角形网格上提出的HWENO 限制器。

激波前后密度、压力变化大,在数值模拟前由于无法预测激波位置,初始网格一般为均匀分布网格,激波附近网格分辨率不足进一步加剧DG方法在模拟强间断问题时的收敛性和鲁棒性问题。 基于以上原因,基于网格自适应和限制器技术开展DG 方法的间断流场数值模拟是重要研究方向,能够提高计算精度,改善激波模拟分辨率。

耦合流动特征、动态调整网格单元分布的r型、h 型网格自适应技术能够改善气动特性计算精度,提高复杂流动模拟精度[10-11],其在误差修正[12]、网格无关性[13]、验证与确认[14]、非定常流动模拟[15]等方面都开展了应用研究。 Karen等[16]在数值模拟飞行器再入过程中采用基于网格点温度的r 型网格点移动方法,引入网格点周围单元的最小内切圆半径及基于雷诺数的网格点目标长度作为控制参数。 从结果看到,该方法实现了r 型网格自适应,在强激波附近聚集2 ～3 层网格。 吴泽艳[17]、孙强[18]等将h 型网格自适应方法应用在二维DG 的激波捕捉方法中,采用HWENO 限制器捕捉激波,有效实现了激波区域的网格自适应加密。 王利和周伟江[19]基于伴随方法开展了网格自适应技术的二维DG 方法研究,提高了计算精度。 Woopen[20]、Fidkowski[21-22]等在DG 方法上建立了基于伴随方法发展网格自适应技术,并将其用于阻力预测,取得了较好的效果。 r 型网格自适应方法[23-24]作为一种激波捕捉和误差估计方法,通过移动网格点使网格聚集在流动变化剧烈区域,实现对流动特征区域网格加密,改善网格分辨率,提高流场模拟精度和气动特性求解精度。 r 型网格自适应的最大优点是网格单元的连接关系和网格的空间拓扑结构在自适应迭代过程中始终保持不变,流场解算器在运行过程中不需要调整网格数据结构,不必考虑并行动态负载平衡问题。

本文针对DG 方法在数值模拟强间断方面存在的计算收敛性差、鲁棒性低的问题,建立了一种基于网格点压力和网格点相对位移变化为控制参数的r 型网格自适应方法及Venkatakrishnan 限制器来提高DG 方法模拟强间断流场的能力。 重点介绍了r 型网格自适应独特的网格点移动驱动策略;Venkatakrishnan 限制器考虑了DG 方法高斯数值积分的特殊性。 首先,给出了DG 方法,包括控制方程、空间离散、时间离散和Venkatakrishnan限制器;其次,介绍了r 型网格自适应方法,详细给出了网格移动策略;再次,采用NACA0012 翼型跨声速绕流验证DG 方法及限制器;然后,数值模拟了并列NACA0012 翼型超声速流动,验证了二维流动下本文r 型网格自适应和限制器技术;最后,模拟了三维双半球-圆柱流动干扰流动,验证了基于r 型网格自适应的DG 方法在激波捕捉方面的能力。

1 间断Galerkin 有限元方法

1.1 控制方程

1.2 DG 方法空间离散

空间离散前,整个求解区域Ω被划分为互不重叠的非结构单元Ωk,对于三维问题,Ωk包括三棱柱、四面体、六面体和金字塔。

将方程(1)两端乘以测试函数ϕj(x,y,z),再在单元内积分,并使用分部积分方法得到DG 的弱形式。

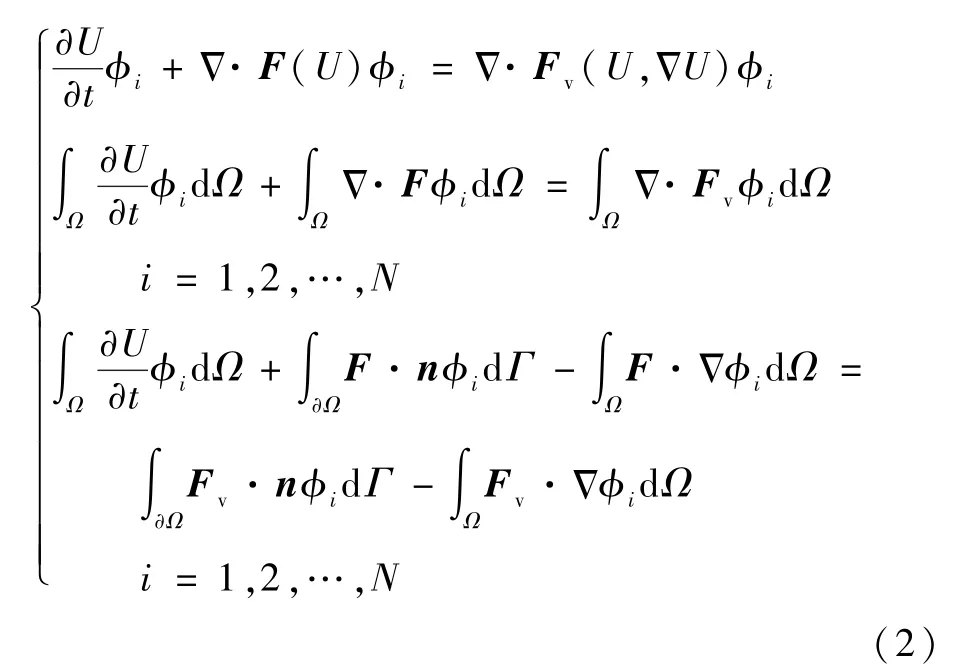
式中:n为单元边界面的外法向;∂Ω为单元Ω的边界;Γ为单元Ω的边界∂Ω的微分符号。

假设变量在单元内具有以下多项式分布:

1.3 DG 方法时间离散

对方程(4)采用一阶欧拉后差:

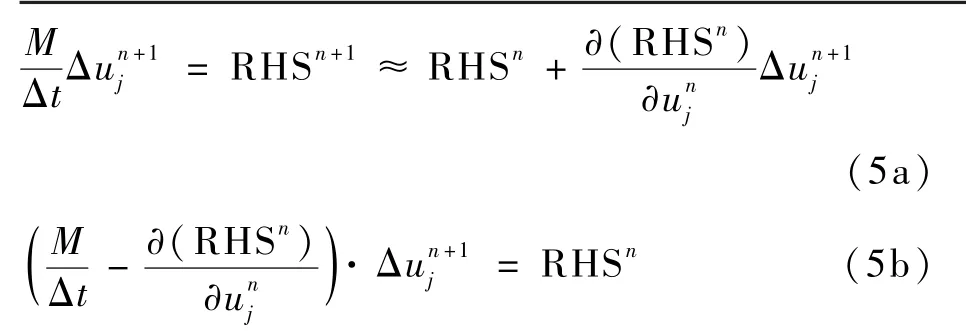
本文采用LU-SGS 隐式离散[25]求解该线性系统,求解过程中引入局部时间步长、变CFL 数等加速收敛技术。

1.4 Venkatakrishnan 限制器

为保证计算鲁棒性,在间断区域及网格质量较差区域,采用限制器来抑制震荡DG 方法的限制器可能带来计算精度降低、残值收敛滞止问题。DG 方法作为一种内自由度方法,具有模板紧致特性,这要求限制过程也能保持紧致特性。 有限体积的斜率类限制器通过改进后能用于DG 方法,其核心思想是:限制单元变量梯度,使单元任何一点变量值不超过相邻单元的最值,防止出现“过冲”现象。 Barth 和Jespersen[7]建立了非结构网格中常用的一类Barth-Jespersen 限制器,该限制器在计算限制因子过程中引入不可微函数带来残值收敛性问题。 Venkatakrishnan[8]通过近似min(1,y) 函数避免不可微过程,建立了Venkatakrishnan 限 制 器。 Venkatakrishnan 限 制 器 由于其较好的残值收敛性、鲁棒性和计算精度而得到了广泛应用。 本文参考有限体积法中这类限制器的构造原理,得到适合DG 方法的斜率限制器。

判断当前单元所有边界面的高斯积分点变量值是否满足以下条件:

积分点限制因子αj具体形式如下:

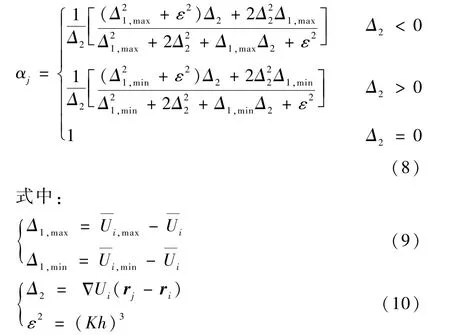
其中:K为量级为1 的自由可调参数,其大小影响残值收敛性,值越小代表限制越大;h为单元的参考长度。

韩国的风水说主要应用于墓地、部落等的选址以及都城、寺刹、住宅等建造方面。 就墓地而言，中国道教风水学说传入朝鲜半岛后，古代朝鲜人民也认为如果把祖先葬在藏风纳气的风水宝地上，这种“佳吉气”就会感应到子孙后代身上，让子孙繁衍昌盛； 如果祖先所葬之地没有“气”，则会出现天壤之别的情形。

2 r 型网格自适应方法

r 型网格自适应方法通过移动网格点使网格聚集在流动变化剧烈的区域,实现流动特征区域网格加密,改善网格分辨率,进而提高流场模拟精度。 网格自适应技术主要包括误差估计、网格加密/稀疏、表面网格投影、空间体网格匹配及并行实现。

本文r 型网格自适应方法在自适应过程中限制表面网格点移动,因此不考虑表面网格投影。r 型网格自适应在自适应过程中网格单元的连接关系和网格空间拓扑结构保持不变,也不考虑并行问题。 本文重点介绍r 型网格自适应网格点移动策略。

Karen 等[16]采用温度作为网格点移动控制变量适合高超声速流动,对于一般的跨声速或超声速流动基于压力变化可能更具有普适性。 从文献[16]算例看到,基于单一的温度作为控制参数,网格自适应区域的网格聚集数较少,经过100 次自适应迭代后,只有2 ～3 排网格点移动,激波附近网格点移动信息向其周围网格点传递不明显。

本文r 型网格自适应网格点移动的驱动力由网格点的流场变量值确定,以归一化网格点的变量差及网格点相对位移量这2 类参数作为网格点移动的权函数。 针对激波问题,本文以压力P作为网格点移动控制变量。 网格点移动的计算流场如图1 所示。

图1 r 型网格自适应网格点移动位移计算流程Fig.1 Calculation process of grid point displacement in r-grid adaptive

以图2 为例具体说明网格点移动控制过程。

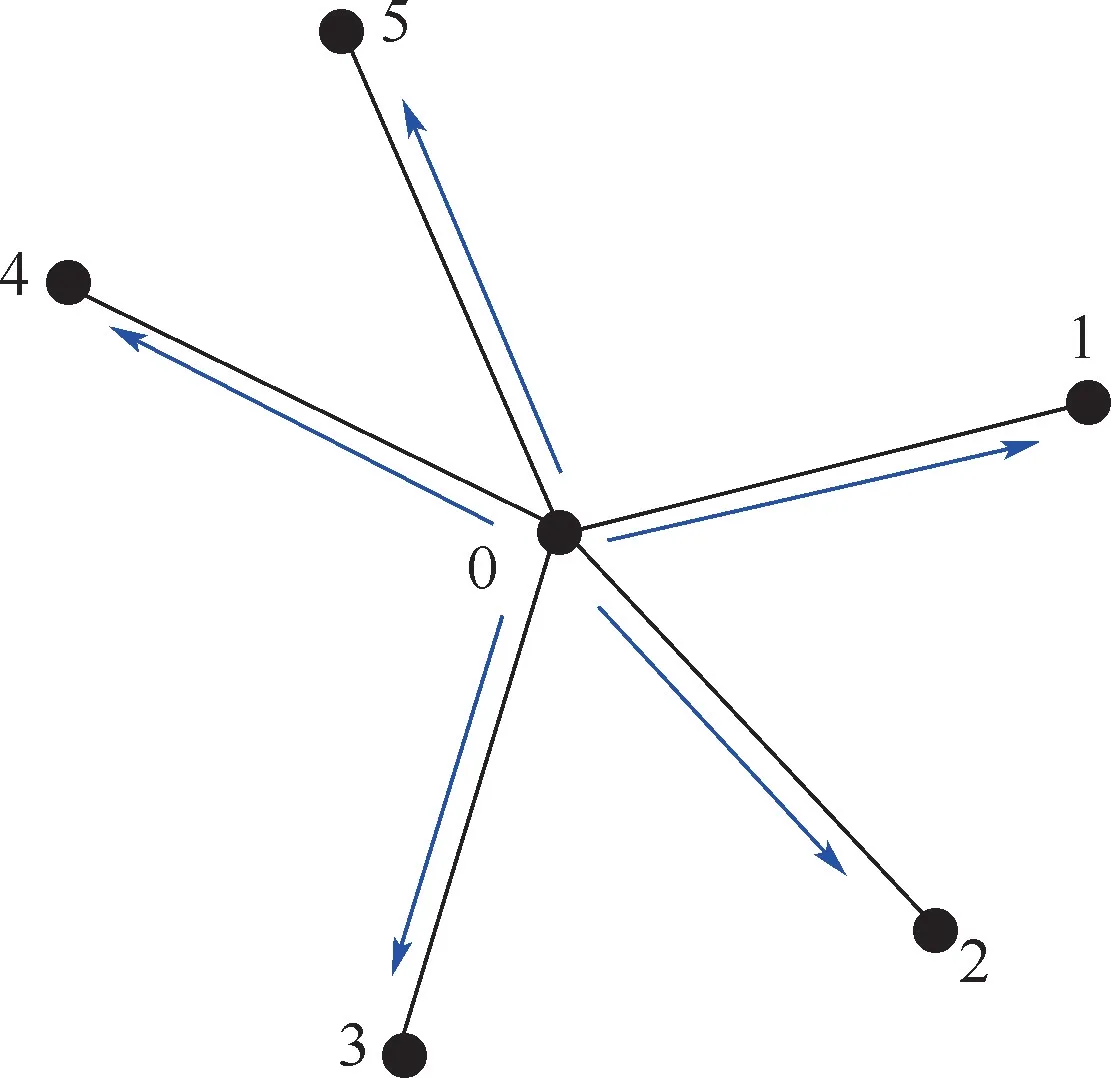
图2 网格点分布示意图Fig.2 Distribution diagram of grid points

1) 采用距离权计算网格点0 及周围网格点1、2、3、4、5 的压力。

7) 限制特殊点的位移,如对称面上网格点y方向位移为零(对称面在y=0 平面)。

8) 移动网格后检查网格质量,如果出现负体积,则修改移动量Δr0,Δ˜r0=C·Δr0,C为限制系数,本文取0.5,并再次检查网格质量,如果出现负体积,再按Δ˜r0=C·Δr0减小移动量,直到体积正常。

3 数值算例

本文所有算例都在中国空气动力研究与发展中心的计算机群上完成。 首先,采用NACA0012翼型验证本文DG 方法和Venkatakrishnan 限制器;然后,采用典型超声速二维及三维流动算例展示r 型网格自适应方法在DG 方法的激波捕捉技术中的应用能力。 算例表明,本文限制器方法具有较好的鲁棒性,能够处理各向异性网格及网格尺度急剧变化的网格。

3.1 DG 方法及其限制器验证

图3 NACA0012 翼型计算网格Fig.3 Computational grid of NACA0012 airfoil

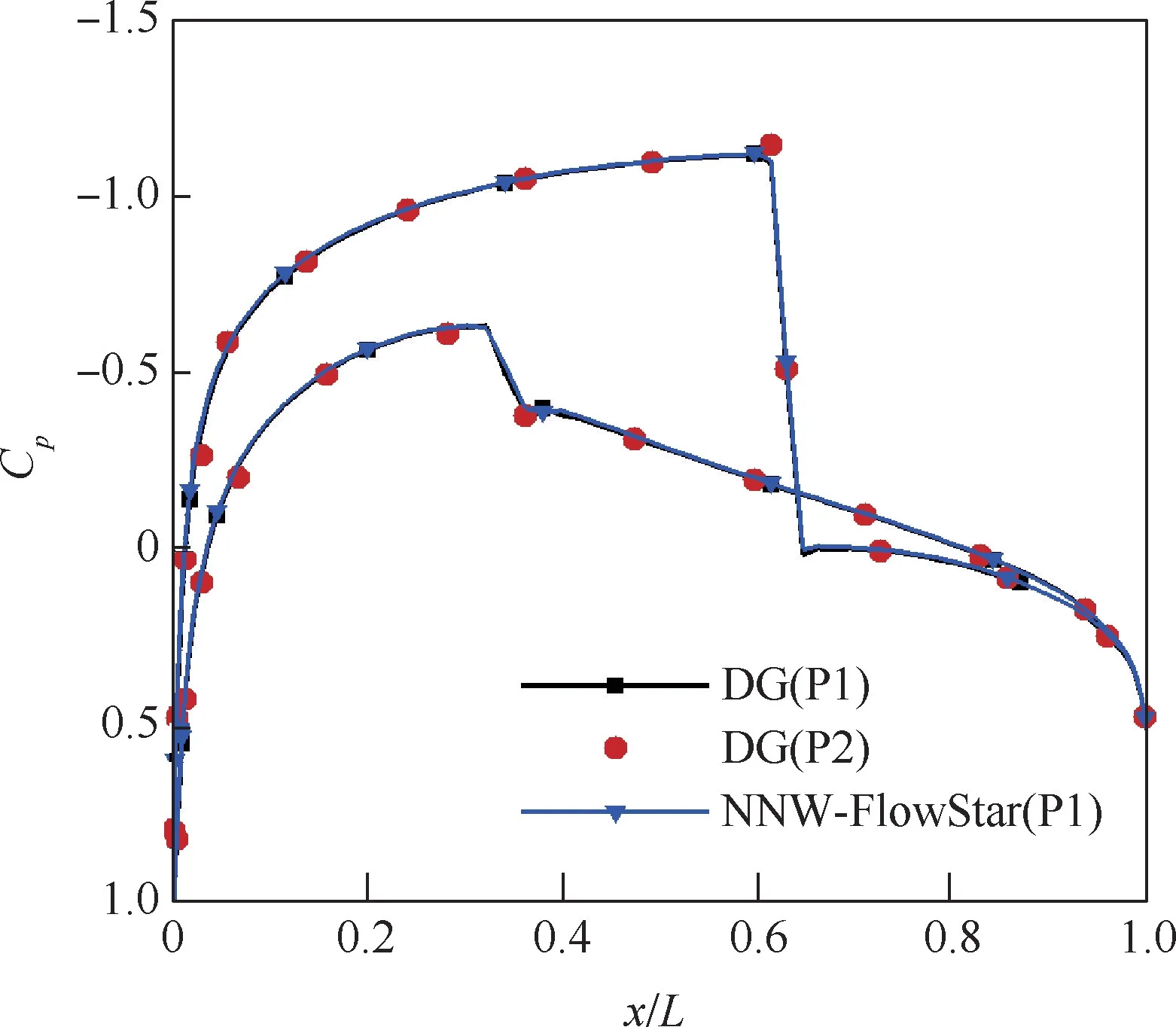
图4 不同方法压力分布比较Fig.4 Comparison of pressure distribution between different methods

3.2 并列两段NACA0012 翼型超声速绕流

本节数值模拟了2 个并列放置的NACA0012翼型的超声速绕流。 计算的初始网格如图5 所示,远场为30 倍弦长,共25 982 个三棱柱单元,展向拉伸一排网格。 其中一个翼型相对另外一个翼型上移和后移0. 5 m,计算来流马赫数Ma=2.0,来流迎角0°,来流静压P=26 500 Pa,来流静温T=223.25 K,自适应迭代11 次,在自适应迭代中保持翼型表面网格点不移动。

翼型错位放置,翼型间产生复杂的激波干扰,上部翼型的脱体激波在下部翼型的上表面产生反射激波后反射到上部翼型的下表面。 图5 ～图9分别给出了初始网格、第1 次自适应、第3 次自适应、第5 次自适应、第11 次自适应后的网格分布及压力系数空间分布。 可以看到,初始网格和自适应后的网格都捕捉到脱体激波及翼型间的反射激波;r 型网格自适应方法准确判别到流场剧烈变化区域,并将网格沿着激波方向各向异性自适应聚合,自适应后的激波捕捉更清晰和锐利;随着自适应迭代次数的增加,激波附近的网格逐步被自适应加密,网格更紧密聚合于激波处,约有4 ～5排网格,捕捉激波的网格宽度更小,拉伸比更大。自适应方法同样也准确识别翼型之间的反射激波,并沿激波方向进行了自适应加密。

图7 NACA0012 翼型第3 次自适应后计算网格及流场Fig.7 Computational grid and flowfield of NACA0012 airfoil after third r-adaptation

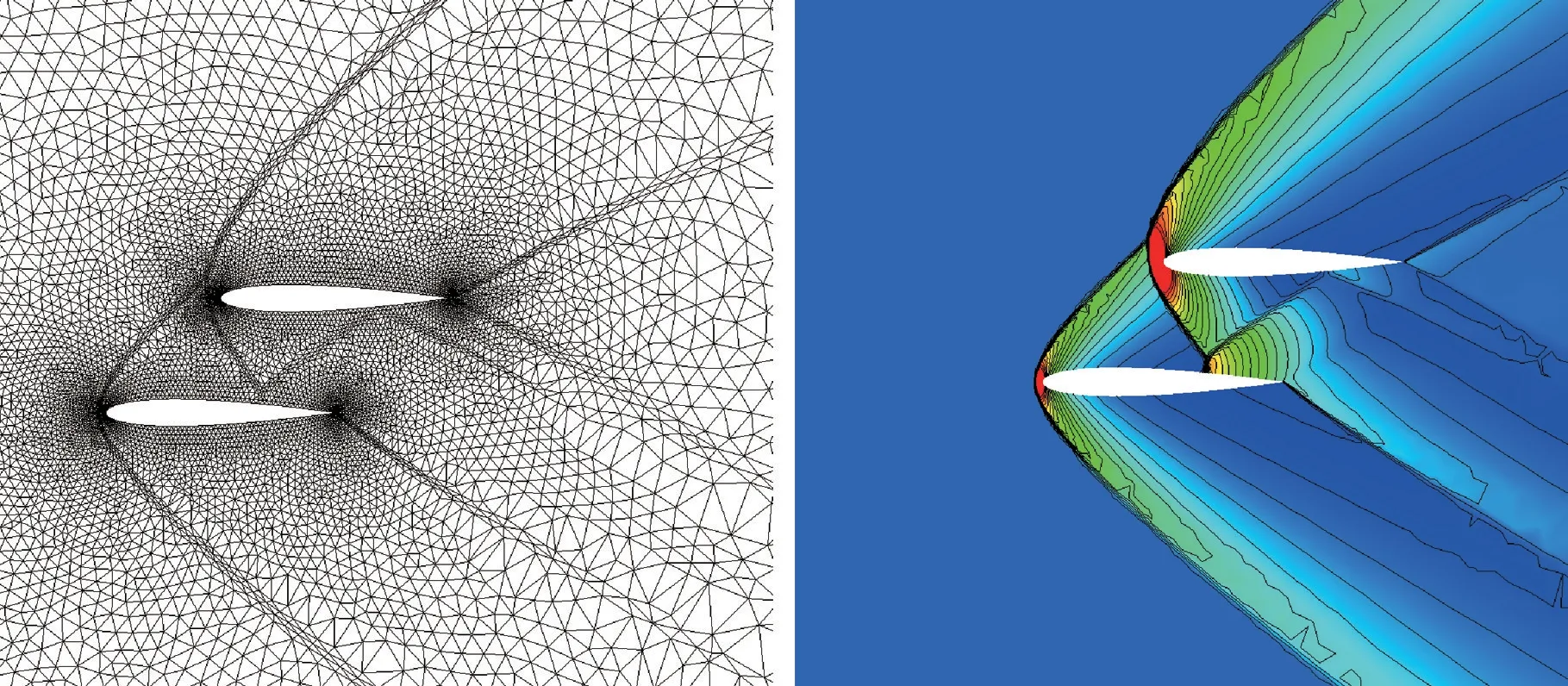
图8 NACA0012 翼型第5 次自适应后计算网格及流场Fig.8 Computational grid and flowfield of NACA0012 airfoil after fifth r-adaptation

图9 NACA0012 翼型第11 次自适应后计算网格及流场Fig.9 Computational grid and flowfield of NACA0012 airfoil after eleventh r-adaptation

图10 给出了第11 次网格自适应后翼型脱体激波附近网格放大图。 自适应后,激波附近网格拉伸比变大,网格尺寸剧烈变化,网格质量变差,本文的Venkatakrishnan 限制器能够很好处理该类网格,保证DG 方法计算的鲁棒性。 图11 给出了空间截面位置,图12 和图13 分别给出了空间截面z=0. 25 m 和z=0. 068 m 处的压力分布。可以看到,自适应前后DG 方法都能够捕捉激波,随着r 型网格自适应迭代,网格逐步向激波位置聚集,DG 方法捕捉激波更加清晰,主要表现在跨过激波前后压力峰值更大,激波宽度更窄,激波更锐利。 从图12 看到,在自适应迭代11 次后,数值模拟的激波变化已经很小。

图10 自适应网格局部放大图Fig.10 Local enlarged view of adaptation grid

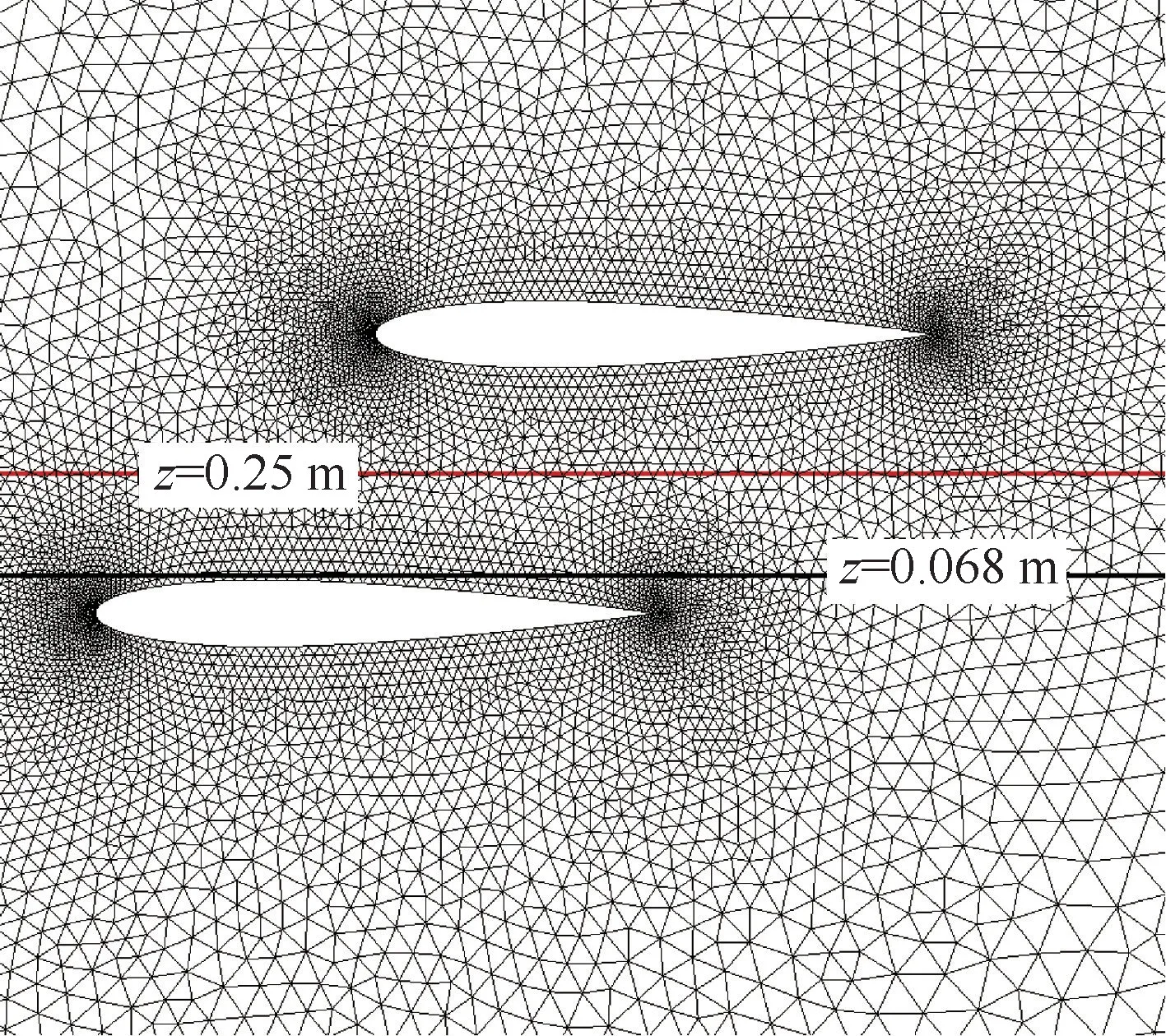
图11 空间截面位置Fig.11 Space section position

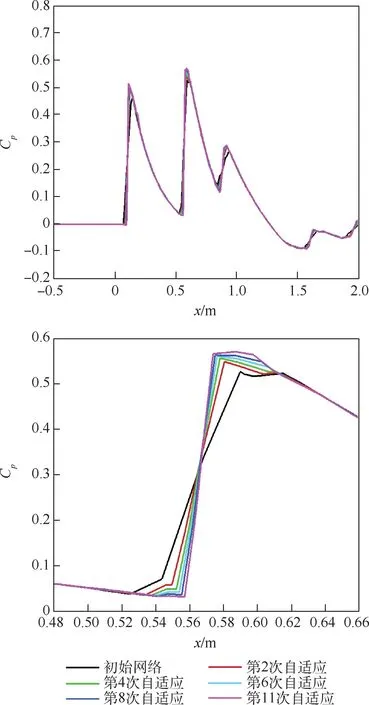
图12 z =0.25 m 处压力分布及激波处局部放大图Fig.12 Pressure distribution at section z =0.25 m and local enlarged view of shock wave

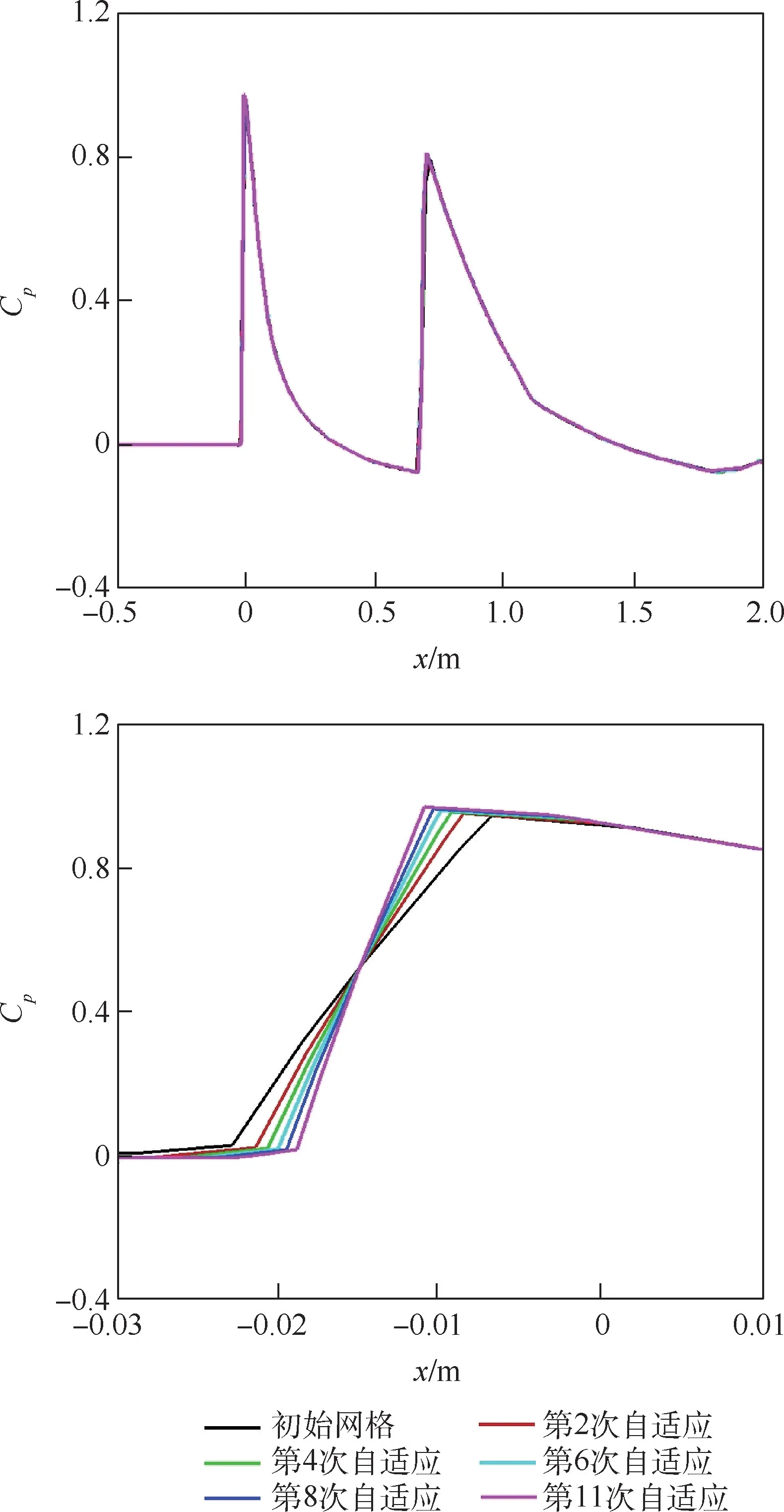
图13 z =0.068 m 处压力分布及激波处局部放大图Fig.13 Pressure distribution at section z =0.068 m and local enlarged view of shock wave

图14 展示了自适应计算过程中翼型阻力系数CD随计算步数变化曲线。 阻力系数在每次网格自适应后只需较小计算步就收敛,随着自适应迭代增加,阻力系数增加量逐渐减小。

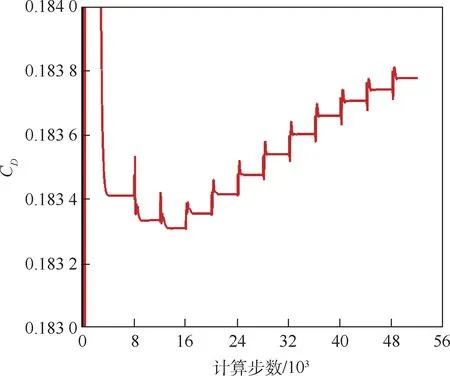
图14 自适应过程阻力系数随计算步数变化曲线Fig.14 Curve of drag coefficient varying with iteration steps in adaptive process

图15 给出了阻力系数和Venkatakrishnan 限制器系数平均值随自适应迭代步变化曲线。 阻力系数随网格自适应迭代逐步增大,斜率逐步减小,限制系数平均值及其斜率随网格自适应迭代步数都逐步减小。 网格自适应步数越大,网格拉伸比越大,网格分布呈现更加不均匀性,因此限制系数会逐渐减小。 但由于网格主要在激波附近发生移动,而数值模拟激波时计算自身就要降阶,此处的网格移动对计算精度影响很小,算例验证了本文r 网格自适应方法、DG 方法及Venkatakrishnan 限制器的鲁棒性。

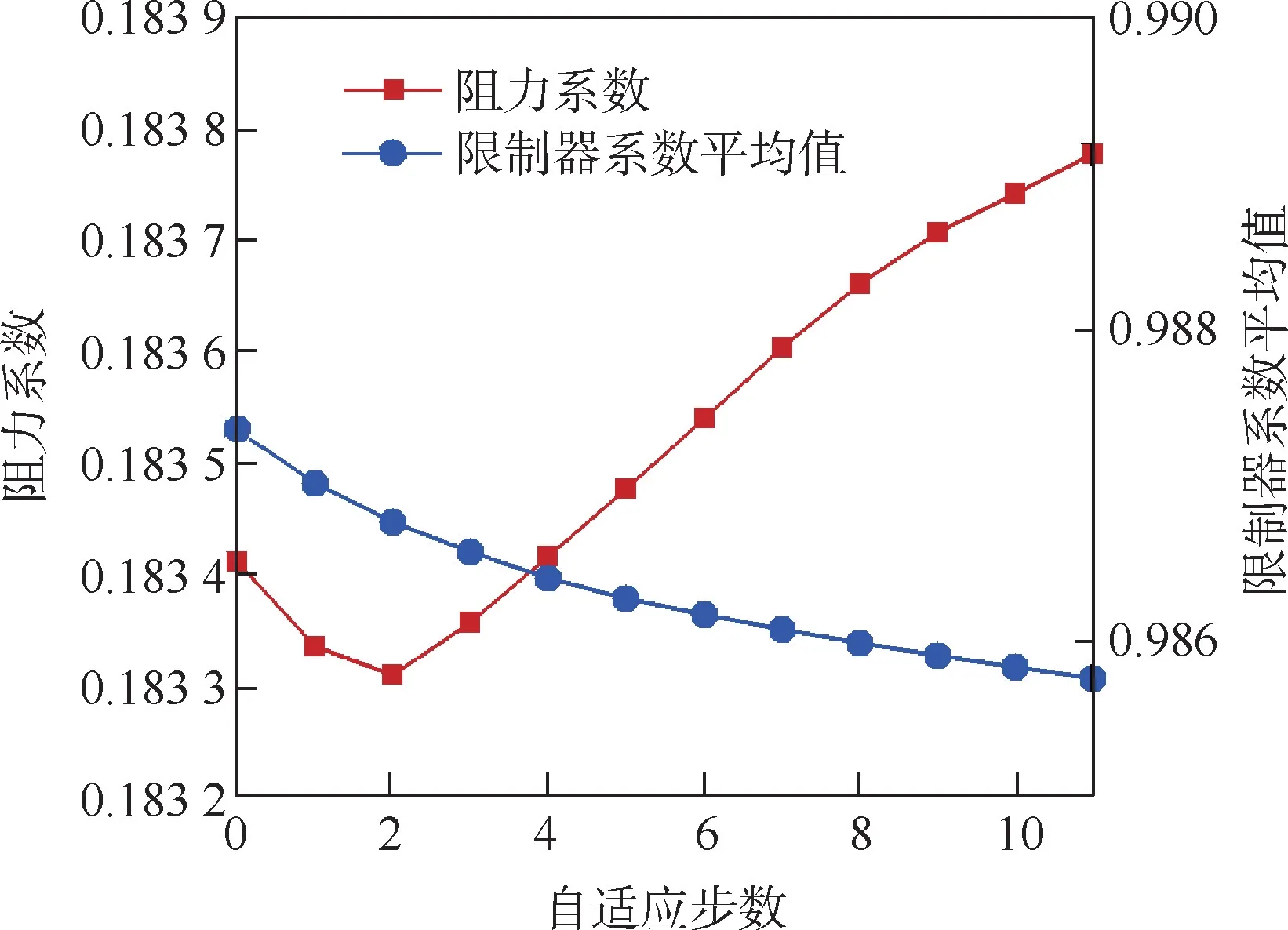
图15 阻力系数及限制器系数平均值随自适应步数变化Fig.15 Resistance and average value of limitation coefficients with adaptive steps

3.3 三维双半球-圆柱流动干扰模拟

为进一步验证本文DG 方法的限制器及网格自适应技术,本节计算了三维双半球-圆柱流动干扰模拟算例。 计算网格如图16 所示,共527 612 个四面体单元。 计算来流马赫数Ma=2.0,来流迎角0°,来流静压P= 26 500 Pa,来流静温T=223.25 K,自适应迭代4 次。 图16 ～图18 给出了双半球-圆柱对称面及表面初始网格和流场、第2次自适应后的网格及流场、第4 次自适应后的网格及流场。 随着自适应迭代步的增加,网格逐步向激波附近聚集,用于捕捉激波的网格的宽度减小,拉伸比增大,激波分辨率增高。

图16 三维双半球-圆柱初始计算网格及流场Fig.16 Initial computational grid and flowfield of 3D double hemispherical cylinder

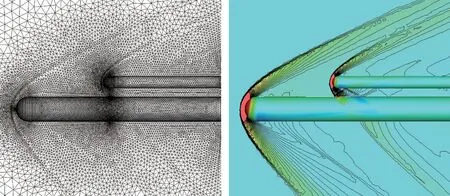
图17 双半球-圆柱第2 次自适应计算网格及流场Fig.17 Computational grid and flowfield of double hemispherical cylinder after second r-adaptation

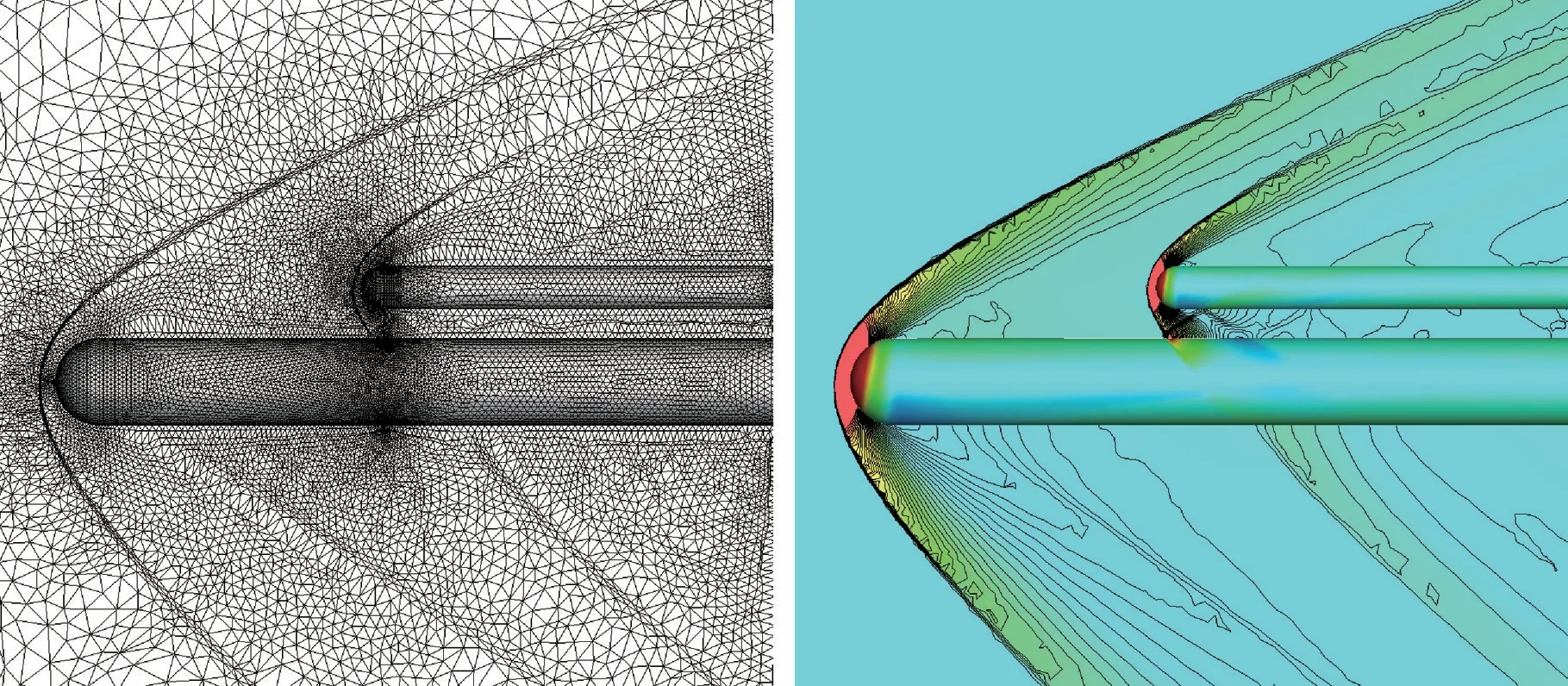
图18 双半球-圆柱第4 次自适应计算网格及流场Fig.18 Computational grid and flowfield of double hemispherical cylinder after fourth r-adaptation

图19 ～图21 给出了x=0.22 m 处的初始网格及流场、第2 次自适应后的网格及流场、第4 次自适应后的网格及流场。 从图21 看到,r 型网格自适应后空间网格向激波附近聚集,来自上部圆柱的脱体激波打到下部圆柱,其激波分辨率提高。

图19 双半球-圆柱初始x =0.22 m 处空间网格及流场Fig.19 Spatial grid and flowfield at x =0.22 m section of double hemispherial cylinder

图22 给出了自适应前后对称面上z=0.04 m截面压力分布。 自适应后激波宽度减小,激波前后压力峰值更大。 图23 和图24 分别给出了自适应前后下部圆柱和上部圆柱y=0 截面表面压力分布。 自适应后影响上下圆柱压力分布,由于本文的r 型网格自适应未移动表面网格,影响量较小。 图25 给出了x=0.22 m 截面处下部圆柱的表面压力分布。 上部圆柱的脱体激波在此处打到下部圆柱,看到自适应前后该处的压力有明显变化,自适应后的表面压力更低。

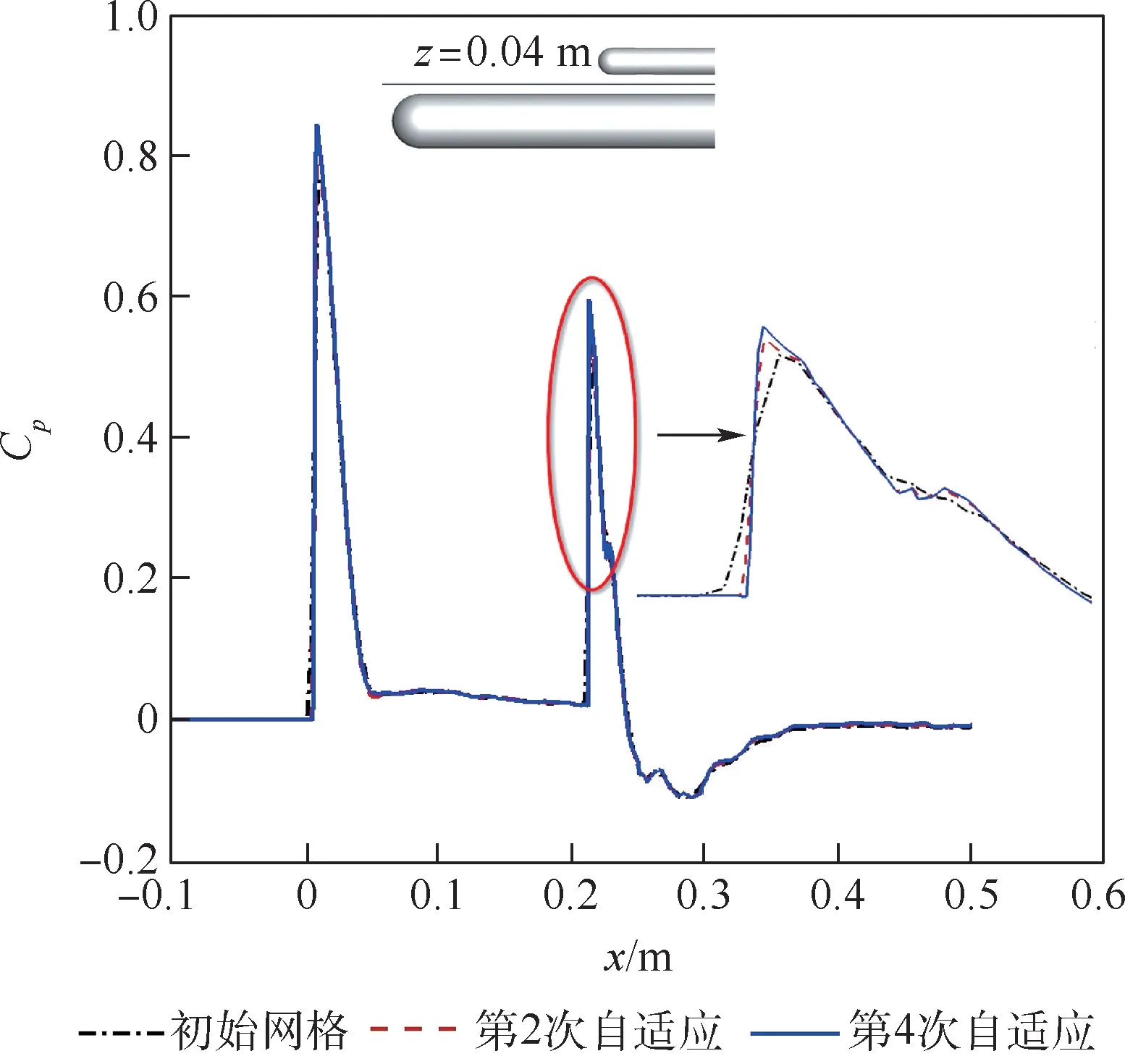
图22 自适应前后对称面z =0.04 m 截面压力分布Fig.22 Pressure distribution at z =0.04 m section of symmetry plane before and after adaptation

图23 自适应前后下部圆柱y =0 截面表面压力分布Fig.23 Surface pressure distribution of lower cylinder at y =0 section before and after adaptation

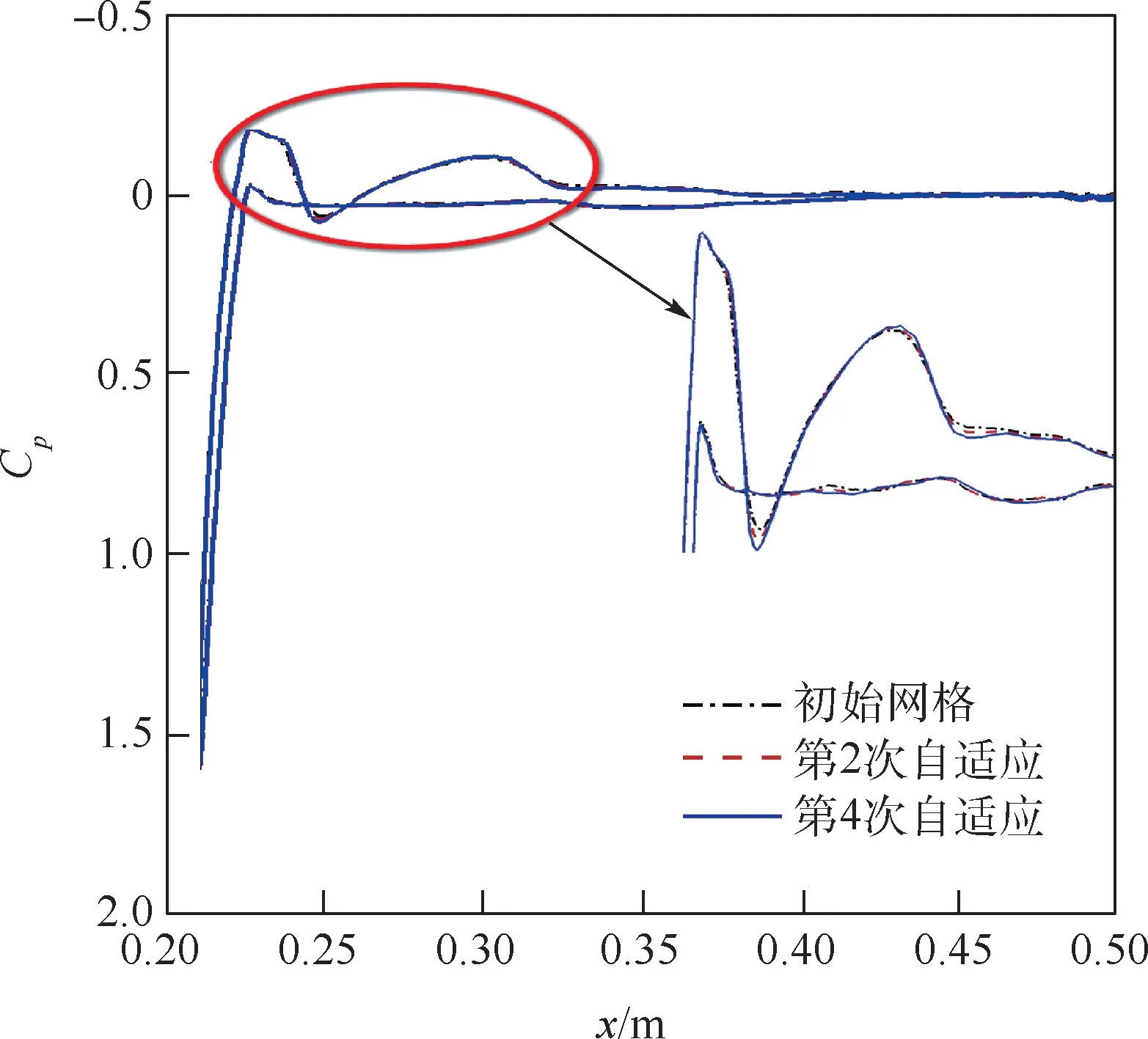
图24 自适应前后上部圆柱y =0 截面表面压力分布Fig.24 Surface pressure distribution of upper cylinder at y =0 section before and after adaptation

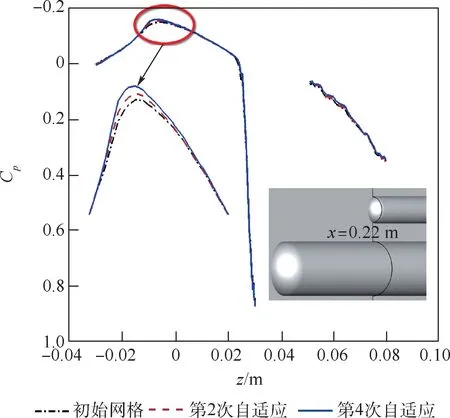
图25 自适应前后下部圆柱x =0.22 m 截面表面压力分布Fig.25 Surface pressure distribution of lower cylinder at x =0.22 m section before and after adaptotion

4 结 论

本文针对DG 方法在模拟强间断流场面临的问题,发展了Venkatakrishnan 限制器和r 型网格自适应方法,通过二维及三维算例分析不同自适应迭代步后的表面和空间压力分布,展示了本文方法在激波精细捕捉方面的能力,并能得到如下结论:

1) r 型网格自适应方法具备根据流场特征开展网格自适应能力,能够沿着激波方向实现网格的各向异性自适应移动加密,具有较好的鲁棒性,保证网格不出现负体积。

2) DG 方法及Venkatakrishnan 限制器针对超声速问题具有较好的激波捕捉能力,能够鲁棒处理各向异性非结构网格、针对自适应后的相邻网格尺寸差异很大的网格具有较高的计算鲁棒性。

3) 通过在DG 方法上发展r 型网格自适应方法能够明显改善数值模拟强激波能力,提高激波分辨率,进一步提高计算精度。