融合曲率特征的椎体几何形态统计模型构建方法
惠宇, 武君胜, 唐继勇, 张靖, 黄伟
(1.韩山师范学院, 广东 潮州 521041; 2.粤北人民医院, 广东 韶关 510525;3.重庆电子工程职业学院 人工智能与大数据学院, 重庆 401331; 4.西华师范学院 计算机学院, 四川 南充 637002;5.西北工业大学 软件学院, 陕西 西安 710072)
脊椎的三维几何形态统计模型[1]是一类通过分析脊椎脊柱几何形状以此来描述其主要形变参数模型的统称。人体脊椎具有一定的复杂性,若想准确定义和定位椎体的几何结构较难以实现;而更为突出的是,目前在我国,对于不同年龄段的脊椎几何统计模型的数据样本统计较少,从而导致医生们在脊椎疾病的诊疗以及手术过程中,无法实现准确的定位及其配准。
目前,国内外在三维统计模型研究领域尚处于探索阶段,Cootes等[1]建立了2D+3D AAM模型,从而依据该模型特征得到人脸的三维特征;Xiao等[2]构建了基于三维特征点定位的人体颅骨统计模型;Romdhani等[3]提出利用PCA算法建立不同场景下的人脸主动形状统计模型;Christoudias[4]利用相关的线性及非线性算法对人脸统计模型进行建模,从而取得了不错的效果。但现有研究仅仅实现了人体一部分部位诸如颅骨的统计建模,对人体脊椎特别是关于腰骶段等力学分析重点部位的三维几何形态统计模型研究,还有待进一步提高。
为了帮助医生能够快速建立起更为精确的脊椎以及脊柱的三维几何形态统计模型,本文应用统计学的方法和规律,对于人体腰椎进行三维重建,然后基于融合曲率特征的特征点自适应识别和定位;由此可以得到模型的几何形态矩阵;进而运用ICP(interative closest point)[5]迭代算法,对样本矩阵进行对齐及配准;在完成这些工作的基础上,应用主成分分析(principal component analysis,PCA)[6]算法进行大量反复的训练和学习,最终形成较为准确的椎骨几何形态统计模型样本库。
利用本文方法得到的样本库模型可以用来统计某一区域的人体脊柱形态变化以及科学度量,后续得到的点云网格模型也可以通过有限元分析软件进行相关的生物力学分析实验。
1 几何形态椎体统计模型的建立
1.1 特征点定义
在三维图像学中,特征点是具有一定标识意义的相对关键位置三维坐标点,可表征点云内局部的邻域关系,具有特异性和稳定性等特点。就目前来说,国内外还没有权威方法实现对于脊椎特征点的定义和标注。文献[7-8]提出的标记分类定义法可以实现人体脊椎特征点的定位简单抽象化,根据他对特征点的定义,并参考在国际上颅脑特征点标注标准MPEG-4[9](moving picture experts group),将特征点分为2类:第一类是对基本特征的刻画,比如人体器官特征点的描述;另一类是对细节的刻画,比如人脸以及脊椎特征等,由此得到了腰椎的69个三维特征点。图1标记了人体脊椎腰骶段从右侧面观察时的特征点,图2则标记了俯视人体脊椎腰骶段时所得出的特征点。

图1 脊椎腰骶段的右侧面 图2 脊椎腰骶段的上面 观察特征点标注图[10] 观察特征点标注图[10]
1.2 椎体三维模型构建
本文采用MC(marching cube)面绘制算法基于真实的人体脊椎CT影像数据完成人体腰骶段模型的三维重构[11]。图像显示及增强技术采用开源的VTK(visualization toolkit)视觉化工具函式库进行渲染,VTK库包采用流水线模式进行组件迭代式开发,实现MC面绘制的流程如图3所示。
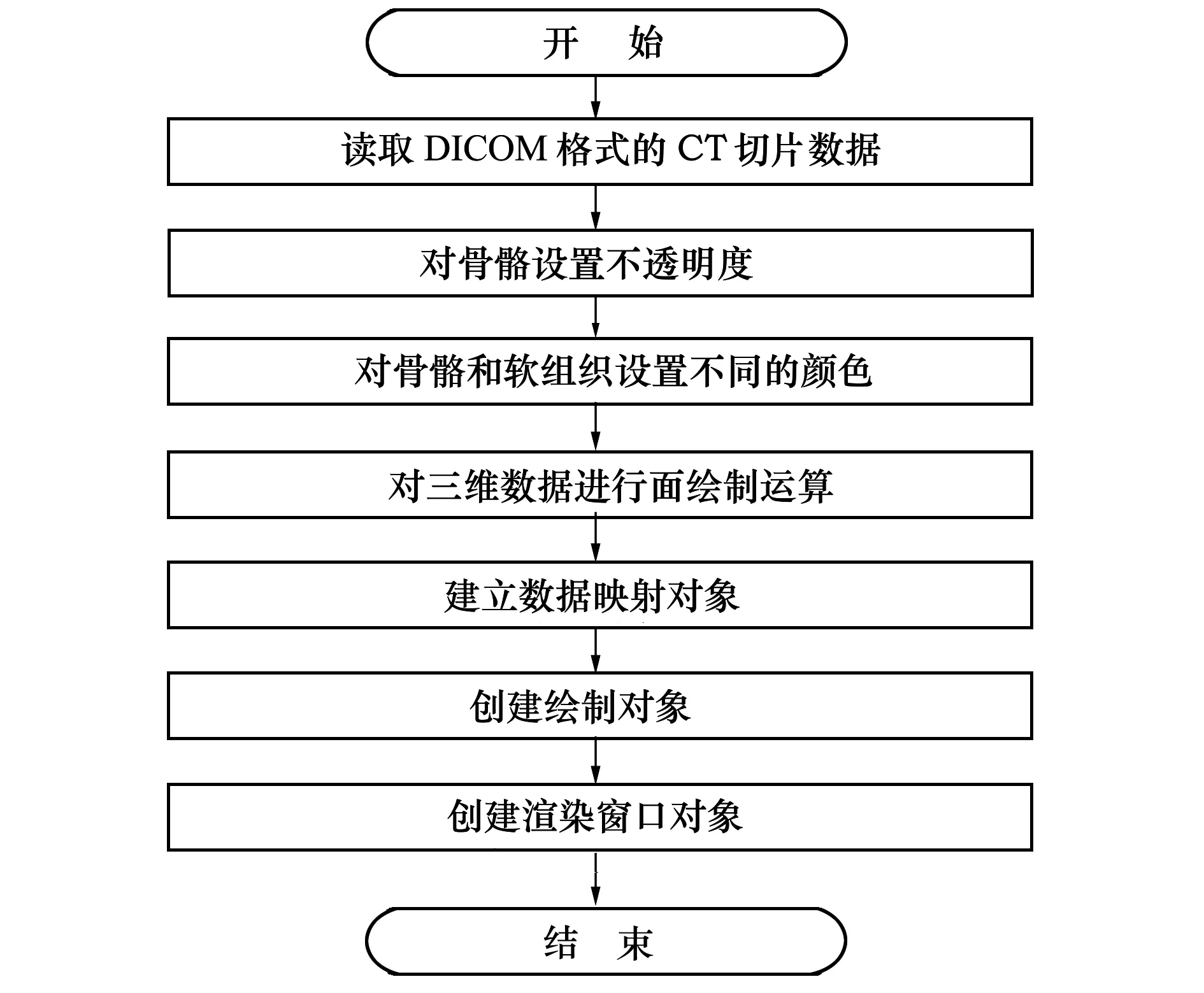
图3 人体脊椎三维重建面绘制的流程[6]
相比于使用传统的光线投射法进行绘制的结果,MC算法的绘制速度快,能够满足对模型进行实时观察的性能要求,使用MC算法进行人体腰椎骨L4段面绘制的结果如图4所示。

图4 人体腰椎骨L4段三维重建后的模型示意图[6]
1.3 融合曲率特征的椎体三维模型特征点标注方法

对于任意点云P={p1,p2,p3,…,pn},穿过其中任意一点pi法线的平面称为该点的法平面。交叉曲面上的点存在无穷多个正交曲率,并且每个点存在一个最大的曲率,那么存在一条曲线上的点满足使得该曲线上的点为交叉曲面上每个点的曲率最大,曲率最大值为kmax,另垂直于最大曲率曲面的曲率最小值为kmin,记作点pi的主曲率k1和k2,从而获得pi的平均曲率,它能表示出这一曲面与周围空间的嵌入关系与形态,公式如(1)式所示。
(1)
点的平均曲率是指该点的极大曲率值和极小曲率值之和的平均值。推导出任意曲面上某一点pi的平均曲率Hk如(2)式所示
(2)
在(2)式中,n是法向量,A是包含点pi在内的无限小区域的邻域面积,diam(A)是该区域的具体直径,相应的梯度用表示。
把(2)式的数据进行离散化,即可得到(3)式

(3)
式中,AM如(4)式所示
式中:αij和βij是两相对角;pj-pi是它们分别所在的三角形的公共边,如图5所示。

图5 相对角示意图[11]
平均曲率Hk可以直观呈现某点pi所在的局部表面的弯曲程度。Hk越大,则意味着该点局部曲面起伏越大,相对于点云中的其他点,该点的几何特征愈加明显。为了提高特征点提取速度,需要将点云中冗余的特征点剔除。通过比较邻域内所有点的平均曲率均值与候选点的平均曲率之间的大小来决定保留或去除该候选点,保留下的点将进入特征点候选几何,平均曲率均值计算公式如(5)式所示
(5)
式中,n是指点云的个数。
基于三维建模分析软件的特征点标记图像如图6~7所示,本文采用融合曲率特征的椎体三维模型特征点标注方法,对所有样本进行了特征点标注,并将每一个样本标定得到的形状矩阵保存起来,形成样本的形状矩阵集合[12],如(6)式所示
{i=1,2,…,n}
(6)

图6 人体腰椎骨L4段右侧 图7 人体腰椎骨L4段上侧面 面观察特征点标记图像 观察特征点标记图像
2 几何形态椎体统计模型的对齐和配准
2.1 基于ICP方法的对齐和配准过程
由于不同模型样本具有自身形状的差异性,基于此,在对样本进行统计建模时会造成结果的偏差。为了提高不同样本之间的相似可比性,需要对训练集中的样本特征形状矩阵进行对齐和配准。就是对模型样本矩阵之间进行相关的旋转或者平移操作,从而使得不同样本间在同一个坐标系中,具有一定的可比性,其过程如图8所示。

图8 样本模型的对齐配准流程图
通过采用快速主成分分析法,标定出m个脊椎样本,可以通过矩阵来表示脊椎形状如(7)式所示
(j=1,2,…,m)(i=1,2,…,n)
(7)
首先第一步在m个脊椎样本训练集中挑选一个大小适中、位置适合的样本Mq(1≤q≤m)作为模型样本,然后剩余的m-1个样本中的任一样本Mp(1≤p≤m;p≠q)作为待配准样本。
通过优化的平移向量和U与旋转矩阵R,将2个样本配准起来,这样2个样本将更具可比性,如(8)式所示
(8)
设3个旋转角度θx,θy,θz分别表示围绕X,Y,Z坐标轴的连续旋转角度。则有旋转矩阵R,如(9)式所示[13]
(9)
在医学上,因为ICP[6]配准方法精度较高,且映射关系在配准前并不需要知道,所以在骨科配准过程中,是较为常见的配准方法。
稀疏矩阵的特点是参数优化过程中计算效率较高。相比较原始模型信息,本文得到的标定采样点集矩阵更倾向于稀疏矩阵。因此本文采用ICP配准方法进行模型的对齐和配准。
ICP的基本思想是寻找与模型样本最佳匹配的待配准样本,即通过矩阵的旋转或者平移变换运算,再应用最小二乘法的迭代思想,使其范围逐步变小,逐渐计算出2个形状矩阵对应点之间的最短距离。
首先为了方便描述,令Q=Mq,p=Mp,则有:
模型样本Q中三维点集为
(10)
待配准样本P中三维点集为
(11)
1) 初始化迭代次数k=0;

5) 计算R×Pk与Qk之间的重心偏差从而获得平移向量U;
6) 进行第k次迭代并进行配准,点集为
(12)
7) 计算点集间的距离
(13)
迭代过程结束的条件:dk+1小于初始距离精度τ或k大于循环次数的最大值。不然重新进入下一轮计算,即进行下一次迭代算法,直至迭代终止的条件满足而终止。
对于ICP的每次迭代操作,使得点集Pk与Qk之间相对应点的距离慢慢变小,使得目标点集M与参考点集P之间越来越接近。直至最后获得与模型样本距离最为相近的匹配样本,如(14)式所示
(14)
2.2 统计模型配准实验结果以及误差分析
本配准实验在Matlab R2013b中进行,选取了30组20~40岁的正常成年男子L4段椎体模型作为样本,对每组样本中69组不同类型的特征采样点进行标注,从而得到不同样本的标注图像及数据集合,对不同样本间图像进行配准实验。
最终配准结果良好,误差较低,从而为后续构建三维统计模型奠定了强大的数据基础[14]。选取样本集合中某例图像样本作为配准实验演示,拾取3个具有代表性的特征点进行配准,配准前的特征点点云阵列如图9所示,配准后的特征点点云阵列如图10所示,由特征点扩张而形成的模型样本点矩阵集则如图11所示。

图9 配准前的特征点点云阵列

图10 配准后的特征点点云阵列

图11 模型样本点矩阵集合
3 建立几何形态椎体统计模型
3.1 基于PCA方法的统计训练
在对集合中所有的样本数据做完配准和对齐后,能够生成m个配准后的样本矩阵。由于每个椎体样本的矩阵维数为3×n,为了实现数据的降维,可以通过使用PCA方法对样本集合进行反复多次训练和学习,进而能够快速准确地获得脊椎样本的平均统计模型。对m个配准后样本进行建模的流程如下:
1) 由三维点集M计算获得一维形状向量X
Xj={x1,y1,z1,…,xi,yi,zi,…,xn,yn,zn}
(j=1,2,…,m)(i=1,2,…,n)
(15)
2) 计算m个样本的平均模型
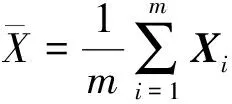
(16)
3) 计算每个样本相对于平均样本X的偏移量dXi
(17)
4) 计算样本几何的散布矩阵S
(18)
5) 计算散布矩阵S的特征值λ、特征向量Φ
SΦk=lkΦk
(19)
式中,λk含义为S的第k个特征值,λk≥λk+1。
并且,Φk含义为形状矩阵变化的应用模式,并且存在(20)式的关系:
(20)
由上述式子可以看出λk和Φk呈正相关关系,λk值越大,Φk体现的矩阵变化模式更为明显。
为了降低矩阵的数据维数,可以使用主成分分析法,对协方差矩阵S的前t个特征值进行降序排列,并结合其对应的特征向量近似地表达出样本的变化情况。
设λT为λk的总和,则有
(21)
公式λk/λT表示模式k对整体模式变化的贡献率,若要得到前t个模式对整体模式的累积贡献率,则用∑λk/λT来表示,其中t需满足(22)式
(22)
式中,用α来表示解释度,α表示当把数据降维后,即计算出的模型能够反应出数据集变化的比例。通常,α的取值都不会小于85%。这样在降维的过程中,即使椎体模型的维度不断下降,却仍然可以表示大多数模型对应的几何形状信息,不会产生较大的偏差[15-16]。
6) 从(19)式的散布矩阵S中取前面t个特征值b(大小为t×1)和其对应的特征向量,共同形成特征矩阵Ψ(大小为3n×t),这样就能得到该椎体集合样本的模型,过程如(23)式所示,其中矩阵X可以表示出训练样本集中的不同形状:
(24)
3.2 统计训练实验结果的验证
对前述30组样本特征集合进行上述统计训练,得到相应的统计训练结果。其统计模型特征值和累计表示度如图12所示, 在对特征值进行降序排序后,可以看出,要使α解析度的值大于85%,只需要选择前28个特征值就可以完成。
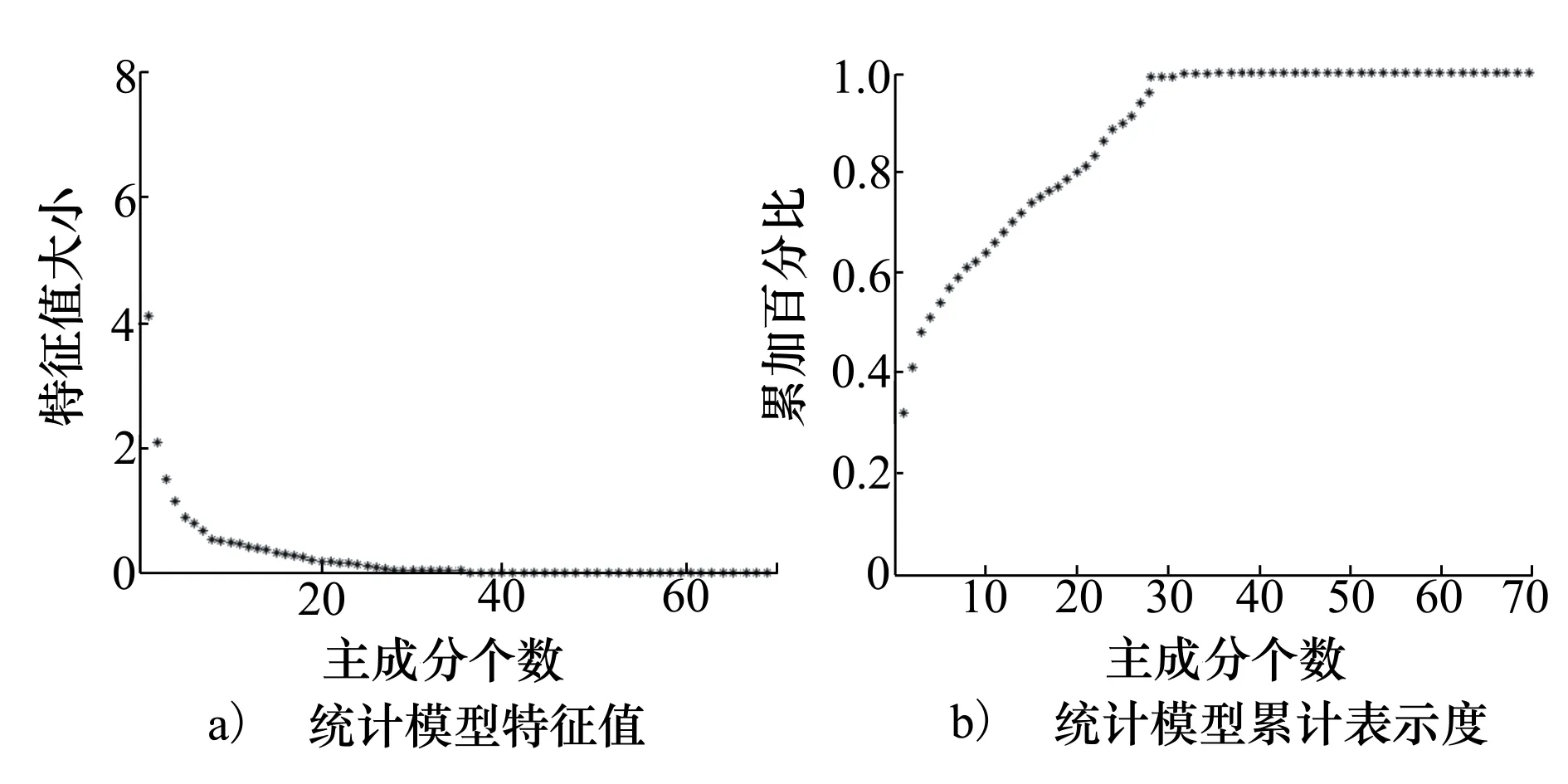
图12 统计模型特征值和累计表示度
4 建立几何形态统计有限元模型

根据上述得到的参数,就能够创建以几何形态为支撑的三维脊椎统计模型,该模型可作为模型样本添加到脊椎的统计样本库中。生成的腰椎L4段几何形态统计模型如图13所示。
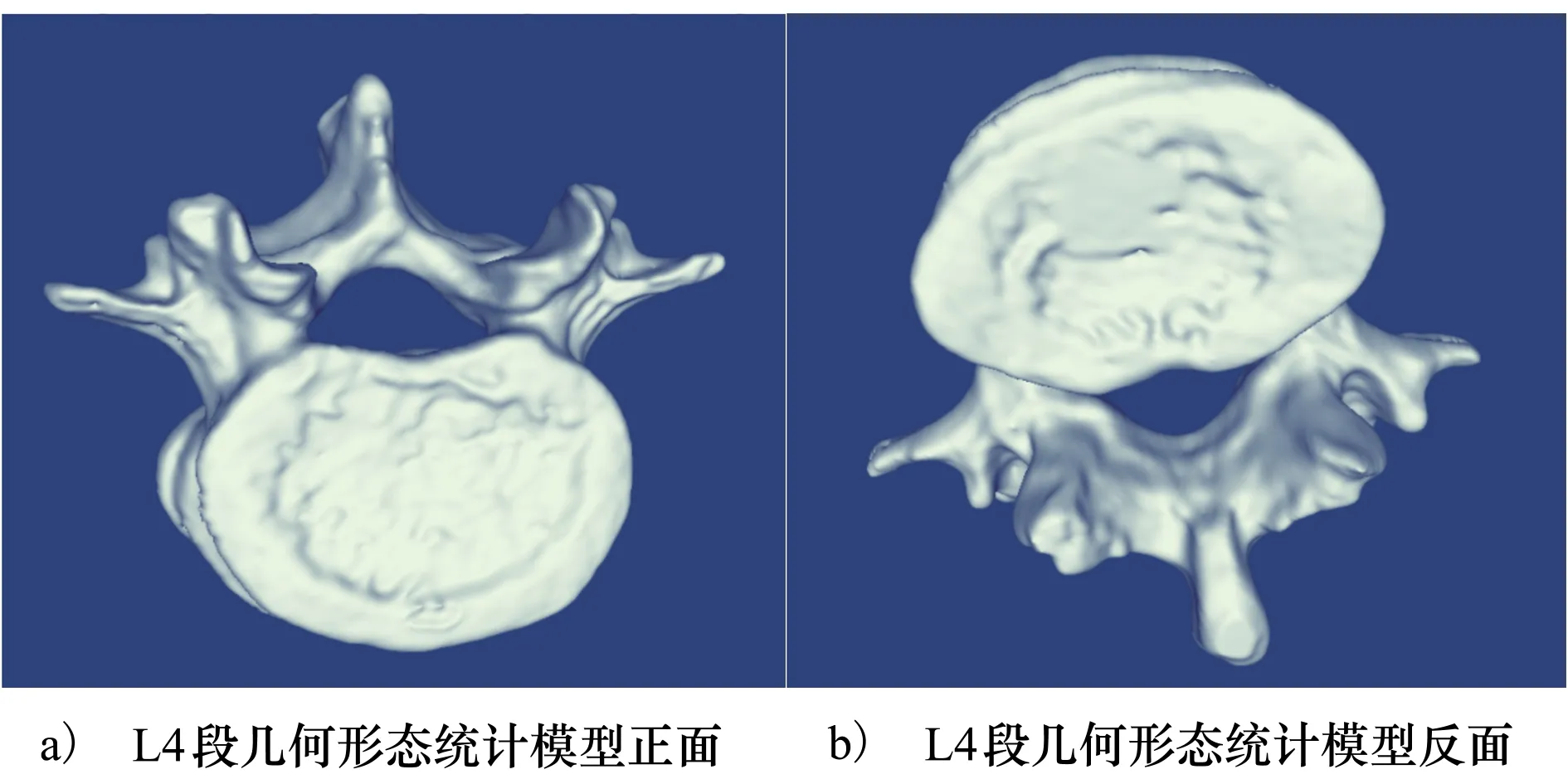
图13 腰椎L4节几何形态统计模型图
5 结 论
本文针对缺乏在不同年龄段中脊椎几何统计模型的数据样本等问题,着手研究并建立了基于融合曲率特征的椎体几何形态统计模型构建方法,从而有助于构建本地区的椎体模型样本数据库;此外,后续得到的点云网格模型也可以通过有限元分析软件进行相关的生物力学分析实验,从而对脊椎方面的病变研究工作提供科学的度量数据。

