基于组合优化算法的翼身融合水下滑翔机优化研究

凌宏杰, 王志东, 张贝, 张代雨, 安帅

(江苏科技大学 船舶与海洋工程学院, 江苏 镇江 212003)

传统的水下滑翔机布局，机身与机翼单独成型，连接处阻力较大，滑翔机机翼窄小，导致升力面面积较小，即使装载较大机翼，升阻比也很难突破5，限制了滑翔效率。美国科研团队采用翼身融合的布局，研发出一代Xray和二代Zray翼身融合水下滑翔机。开启了翼身融合布局应用于水下滑翔机领域的先河。为追求更优异的水动力性能，提升滑翔机的滑翔效率，水下滑翔机的高升阻比优化技术成为研究热点。

水下滑翔机的升阻比优化问题分为2个阶段，首先是参数化建模，将BWBUG的外形定义为参数的形式，指定参数变化区间，生成优化变种模型。其次是优化，通过选定优化方法、约束条件，基于指定的目标函数，进行外形优化。为了解决优化效率和优化精确度的矛盾，代理模型优化方法逐渐应用于水下滑翔机优化设计中。国内西北工业大学和天津大学Yang等[1-2]基于代理模型高维参数化优化方法在水下滑翔机水动力优化方面开展大量研究工作，取得较为丰硕的成果。张代雨等[3]采用NURBS曲线绘制水下滑翔机的参数化模型，充分考虑翼型剖面的放置位置和旋转角度，使用代理模型的方法，对一款翼身融合水下滑翔机升阻比进行优化，优化后的滑翔机升阻比提升18.98%。谷海涛等[4]利用CATIA参数化程序建立传统型滑翔机的参数模型，并基于代理模型进行水下滑翔机机翼优化，使升阻比提升6.76%。孙春亚等[5-6]分别对类椭圆型滑翔机、仿生蝠鲼型滑翔机采用代理模型进行外形优化，使得升阻比分别提升了10.5%,9.1%。李天博等[7]采用CST描形参数化方法，对一款联翼式水下滑翔机基于代理模型进行升阻比优化，使得升阻比分别增加了18.42%。同时，张宁、李成山、叶鹏程等[8-11]采用CST方法建立翼身融合水下滑翔机的参数化模型，以升阻比为优化目标，基于代理模型进行优化研究，使得升阻比分别增加了3.3%，9.35%，4.43%和10%。王新晶、吴序毛等[12-13]采用自由变形(FFD)方法进行几何参数化，使用代理模型的优化框架，分别对Spray的水翼及一款翼身融合滑翔机基于升阻比优化，优化后的升阻比提升了90%，15.53%。

目前国内外很多学者采用代理模型方法开展BWBUG优化设计，该方法在优化参数维度上具有优势，但代理模型的优化和水动力求解是分离的，代理模型的更新需要依据水动力求解数据作为样本点，需手动加载至代理模型中，继续执行代理模型的寻优过程，导致代理模型优化效率较低、耗时长。

组合优化算法为采用不同种优化方法生成不同数量的样本，将所生成样本进行组合，在组合样本中进行目标寻优，充分发挥不同优化算法的优势，规避其缺点，提高可行域内寻优的准确性及计算效率。本文采用正交算法Sobol和遗传算法NSGA-Ⅱ组合优化算法。正交Sobol Method[14]是半随机序列，基于低偏差序列的直升机易损性计算方法。该序列是一种稳定性和覆盖性都非常好的随机序列，与局部法相比Sobol方法参数变动范围可扩展到整个参数定义域；NSGA-Ⅱ[15]是最具影响力的多目标优化算法之一，有3个突出特点：①为了提高算法的收敛速度，采用快速非优势排序；②通过定义拥挤距离，有效避免了共享参数选择的困难；③采用精英策略，保证下一代种群优于上一代种群。

为了进一步挖掘水下滑翔机升阻比特性，引入翼身融合布局，结合Xray设计经验完成滑翔机初始外形设计，基于黏性流体理论，完成BWBUG初始外形水动力预报与分析。基于NURBS曲线绘制BWBUG的精细参数化模型，采用组合优化算法开展高升阻比的BWBUG水动力外形优化，优化过程中直接耦合调用水动力求解软件，提高优化效率。

1 初始外形设计及水动力性能评估

1.1 BWBUG初始外形及网格划分

本文所研究的翼身融合水下滑翔机(BWBUG)布局如图1所示，质量130 kg，依靠浮力调节系统定量调节净浮力大小驱动沉浮，俯仰调节系统负责调节滑翔机俯仰姿态，两者配合，完成水下滑翔机滑翔运动, 左右舷软油囊负责横滚姿态调节和应急处理任务。其水动力外形采用航空领域的翼身融合布局，机身机翼高度融合，结合美国一代翼身融合滑翔机Xray设计经验，充分考虑内部装载需求，完成BWBUG的初始模型设计。该BWBUG是以重心坐标为原心，坐标系如图1所示。其中，X轴正方向指向艏部，Y轴正方向指向左舷，Z轴正方向为垂直机身向上的方向。该BWBUG的机身外形的主尺度参数如表1所示。

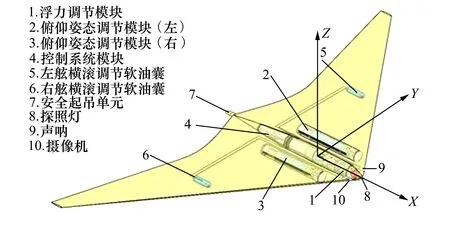
图1 BWBUG总体布局及坐标系定义

表1 BWBUG外形主尺度表

该BWBUG的网格划分，采用滑移网格法，提升网格生成效率、网格质量及边界层y+的一致性。其中：

1) 外域采用矩形域：为了避免外域对水动力求解的影响，矩形域设定为[-12Loa,16Loa]×[-8Loa,8Loa]×[-9Loa,9Loa](Loa为BWBUG的特征长度)；

2) 内域为球域，圆心为BWBUG的坐标原点，BWBUG展向尺寸较大，且为避免滑移网格交界面对翼尖处的流场影响，球域半径设定为3Loa。

采用八叉树算法，生成非结构化网格。以网格正交性为基础，并通过加密准则，调整滑翔机迎流区和尾流区网格密度。经网格收敛性验证，最终确定外域网格量为180万，内域网格量320万。BWBUG网格划分见图2。

图2 网格划分

1.2 网格收敛性验证

计算域生成不同数量网格模型集包含300万,400万,500万和600万，共计4套网格，网格差异主要在本体周围网格区域。选取速度v=0.5 m/s，攻角α=6°工况，采用4套网格计算本体阻力和升力值，从图3中可以看出，当网格数大于500万时，阻力R和升力L计算结果具有一致性，满足网格无关性要求。为提高计算效率，本文滑翔机水动力计算选取网格数为500万。

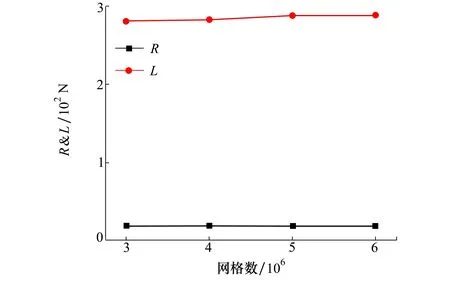
图3 网格数收敛性验证

1.3 计算工况与计算方法

1.3.1 计算工况

为探明翼身融合滑翔机在不同流态下水动力特性，在层流、转捩和湍流3种状态中选取了4个滑翔速度，如表2所示。本文滑翔机的设计航速为v=0.5 m/s。

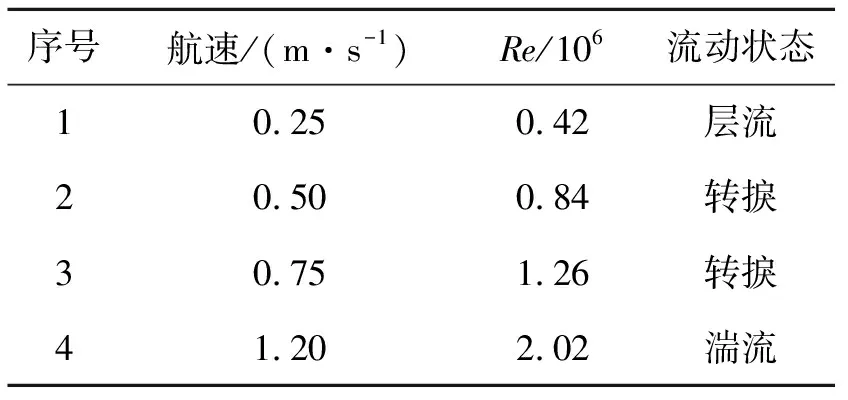
表2 滑翔速度及所处流态

为保证BWBUG在上浮和下潜滑翔模式下具有相同的水动力性能，剖面翼型选取NACA0012对称翼，该翼型不同雷诺数下失速攻角选取0°≤α≤12°，Δα=2°，α=6°附近增加7°攻角，共计32个工况。

1.3.2 计算方法

基于黏性流体理论，开展约束模式下BWBUG水动力数值预报。选择单相流模型，模拟15℃海水，湍流模型为k-ω(SST-Menter)模型，BWBUG本体表面采用标准壁面函数，上下边界为指定压力条件，两侧面为速度远场条件，前后边界为速度入口和出口，详见图4。

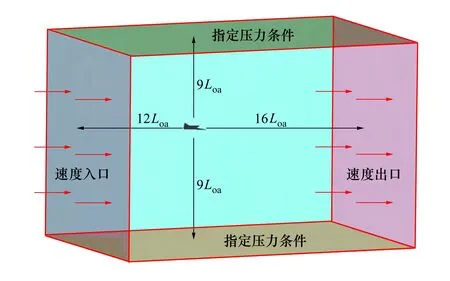
图4 计算域及边界条件

1.3.3 计算方法率定

考虑到BWBUG有关实物试验的公布数据极少。上海交通大学的“海鸥”号主体为鱼雷型，水平侧增加了一对滑翔翼，相较于翼身融合流线构型，滑翔机表面流体压力梯度较鱼雷型小，本文数值方法在鱼雷型水下滑翔机得到验证，表明该数值方法可适用于翼身融合滑翔机。

取 “海鸥”号水下滑翔机在0°攻角，速度为0.2,0.3,0.4,0.5 m/s下的拖曳试验工况，采用本文所建立的数值方法进行模拟。从图5可以看出，数值计算结果与试验对比误差小于2.5%，表明本文所建立的数值计算方法是可靠的[16]。

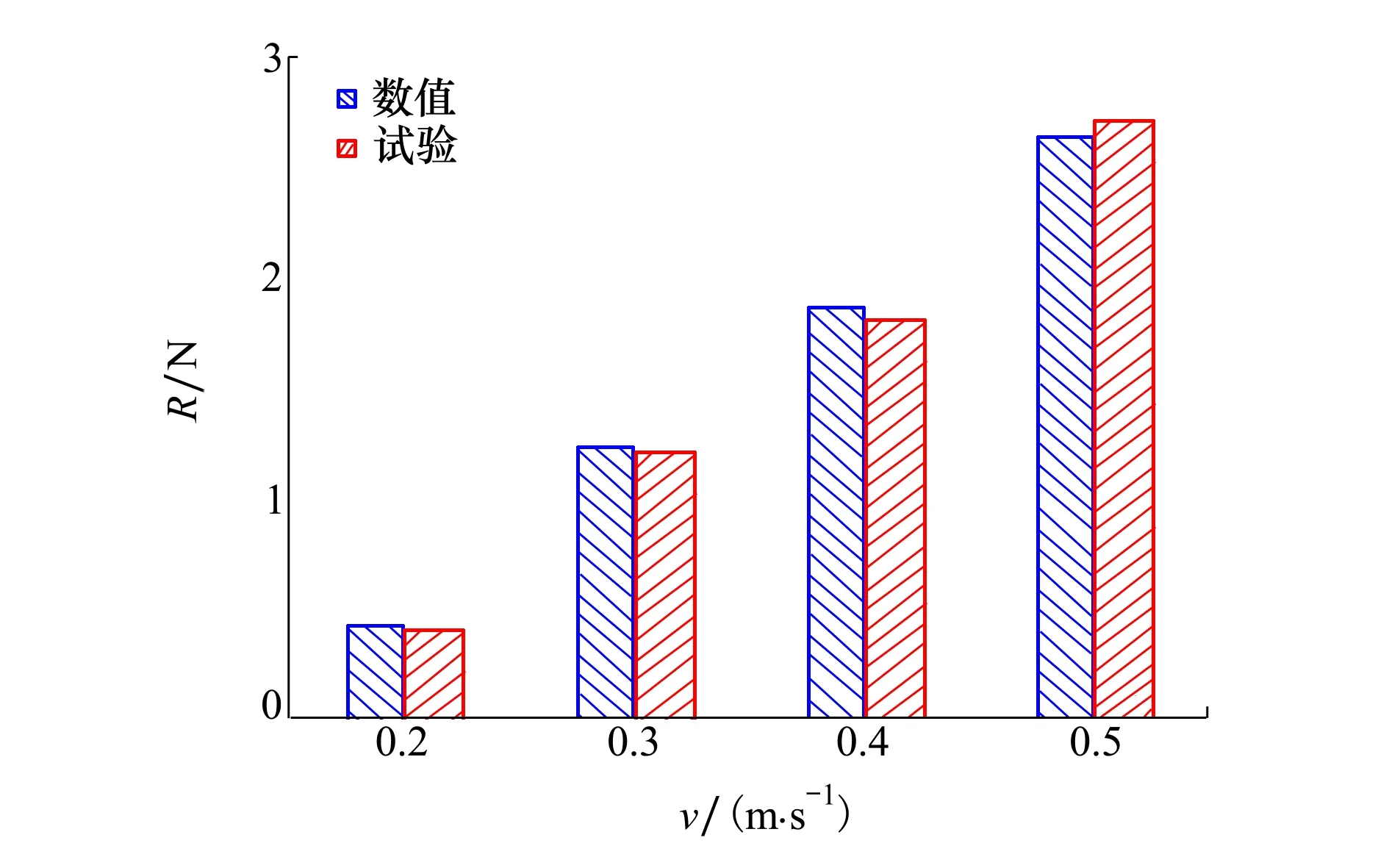
图5 “海鸥”号阻力对比

1.4 初始模型升阻比结果分析

采用本文所建立的数值方法完成不同流态下滑翔机不同攻角的水动力计算，从图6可以看出：当滑翔机设计航速v=0.5 m/s时，BWBUG最高升阻比L/R为15.32，最优滑翔攻角α=6°。

图6 初始模型升阻比图

2 参数化建模与优化方法

2.1 优化与黏流软件接口处理方法

建立BWBUG参数化模型，确定优化方案及参变量设计，编写与黏流软件的接口程序，实现优化程序与黏流软件耦合调用，如图7所示。其优化变种模型的计算方法，依托于初始BWBUG模型数值模拟时录制的可读写、可执行python程序，在设定批处理、并行计算及存储信息后即可运行优化进程，大大提升了优化效率。在优化进程中，可以实时监测优化结果信息，便于及时发现问题并修正。

图7 优化与黏流软件耦合调用流程图

2.2 滑翔机的参数化建模

平面外形是指BWBUG俯视图轮廓线。BWBUG平面外形前缘线AB采用直线程序驱动，后缘线采用NURBS曲线创建，通过设定融合点权重值保证机身与机翼光滑过渡，见图8。BWBUG定义9个平面参数见表3。翼身融合的水下滑翔机参数化模型如图9所示。

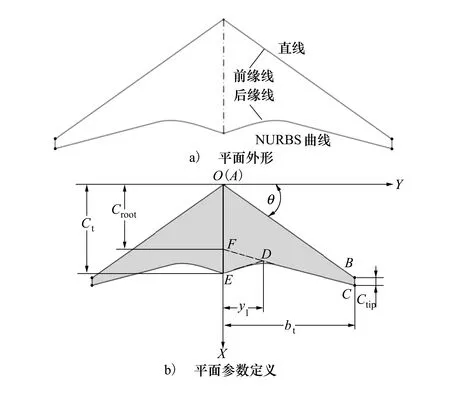
图8 平面外形及参数定义

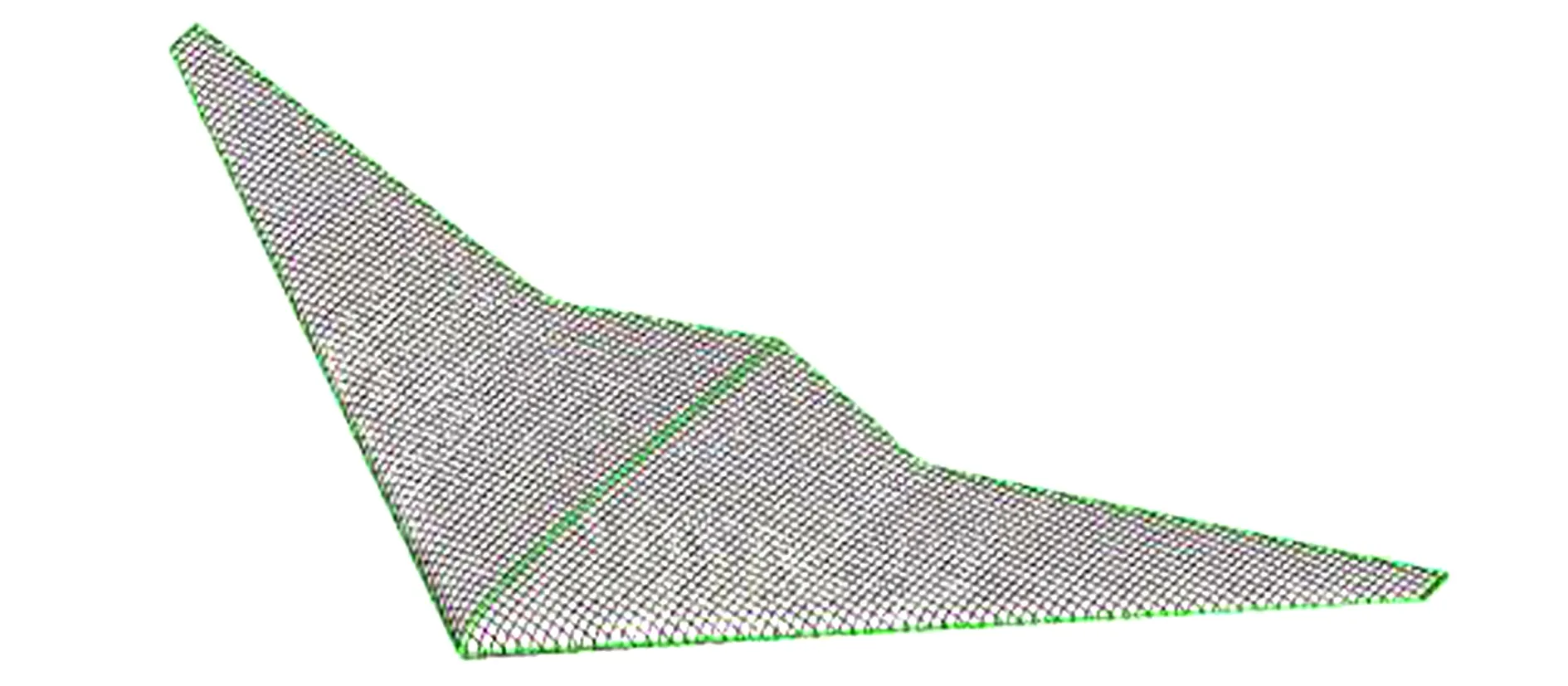
图9 参数化模型

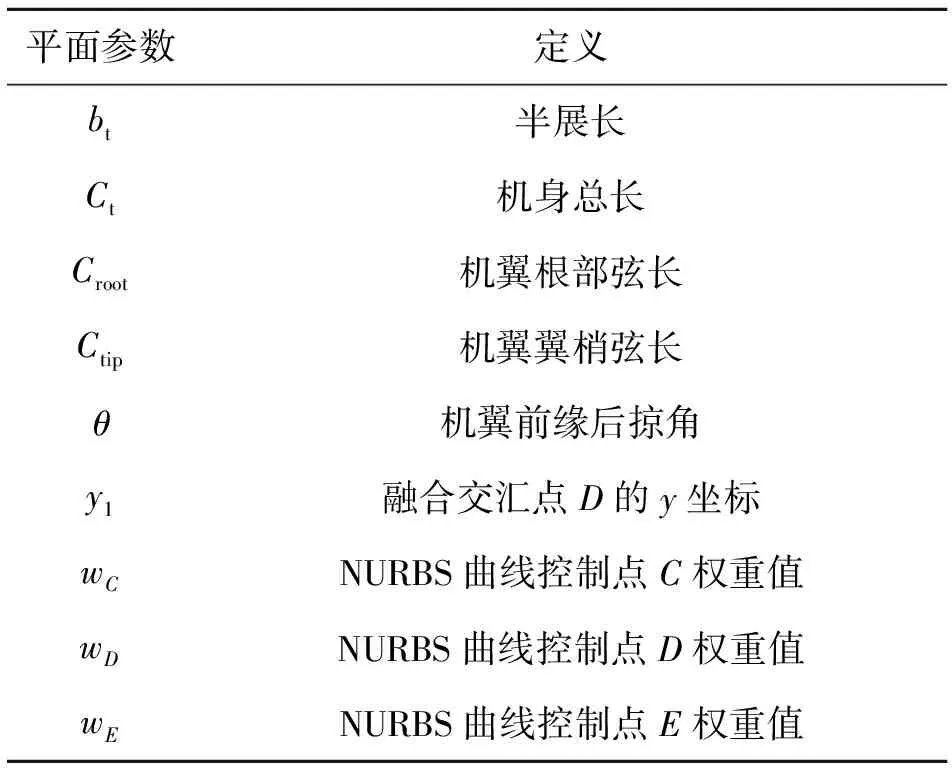
表3 BWBUG平面参数定义

2.3 翼身融合的水下滑翔机模型优化

2.3.1 组合优化算法策略

优化是参数模型的延伸，为了提高优化结果的精度和效率，本文采用组合优化算法[17]，首先使用正交算法Sobol，变量个数为6个，在设计变量区间内给定样本量为64个；然后使用NSGA-II算法生成30个优化模型，进行高升阻比搜索。进化代数为10，交叉概率设定为0.9，变异概率0.2[18]。

2.3.2 设计变量

优化变量选择时，考虑到变种数目约为2N(N为变量数)，所以必须合理控制变量的个数。避免选择过多的优化变量，导致生成变种的数目呈指数倍增加，使得水动力计算的耗时太长。选取6个设计变量：①翼身尾端融合控制点展向相对坐标n1=y1/bt控制滑翔机翼与身尾部融合位置；②展弦比RA=bt/ct控制滑翔机长宽比例；③根梢比RT=Ctip/Croot控制滑翔机翼型根部与梢部比例；④翼根相对弦长CR=Croot/Ct控制翼根与身的比例；⑤正切值tanθ控制翼前缘后掠角；⑥攻角α。调整前5个设计变量即可得到新的翼身融合滑翔机构型，通过第6个变量寻找最大升阻比对应的攻角。

2.3.3 优化目标

本文选取航速v=0.5 m/s下升阻比最大为优化目标。将相同工况下升力和阻力比值作为计算函数，由于优化算法采用最小值寻优，因此将计算函数取负值作为目标函数。

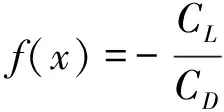
(1)

式中，CL和CD分别为BWBUG的升力系数和阻力系数。

2.3.4 约束条件

滑翔机优化变量取值范围作为约束条件，为了防止出现不切实际的外形，增设强制约束条件。由于BWBUG内部需装载功能舱室及填充浮体材料，应保证一定舱容。滑翔机内部有效空间位于中纵剖面，将中纵剖面的横截面积作为约束条件；滑翔机要满足设备搭载空间，将滑翔机内部容积大于初始仓容作为约束条件。

S′>S

(2)

V′>V

(3)

式中：S′和S为优化后滑翔机的中心横截面积和初始外形中心横截面积;V′和V为优化后BWBUG内部容积和初始内部容积。

3 计算结果与分析

3.1 外形及设计变量对比

表4给出了BWBUG优化前后设计变量取值。可以看出：

1) 设计变量优化后量值均在取值范围内；

2) 优化后的模型，机身中纵剖面长度有所增加，增加有效装载空间；

3) 展弦比及前缘后掠角有所减小，根稍比有所增大；翼尖尺寸减小，有效缓和了翼尖的流场。

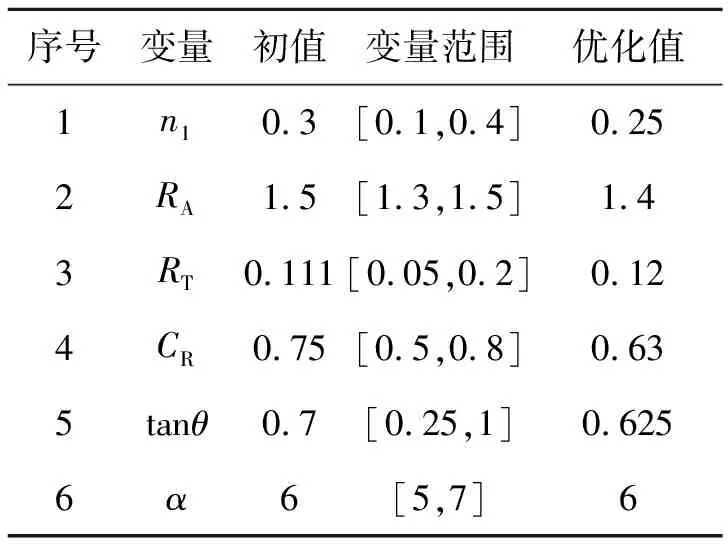
表4 设计变量对比

3.2 水动力性能分析

图10给出了α=6°,v=0.5 m/s上浮优化前后BWBUG表面压力云图，可知：优化前后的模型压力分布规律具有一致性，优化后的BWBUG相较于初始模型，中纵剖面更加丰满，使得滑翔机表面流速变化减缓，层流段长度变长，有助于减小BWBUG黏压阻力。

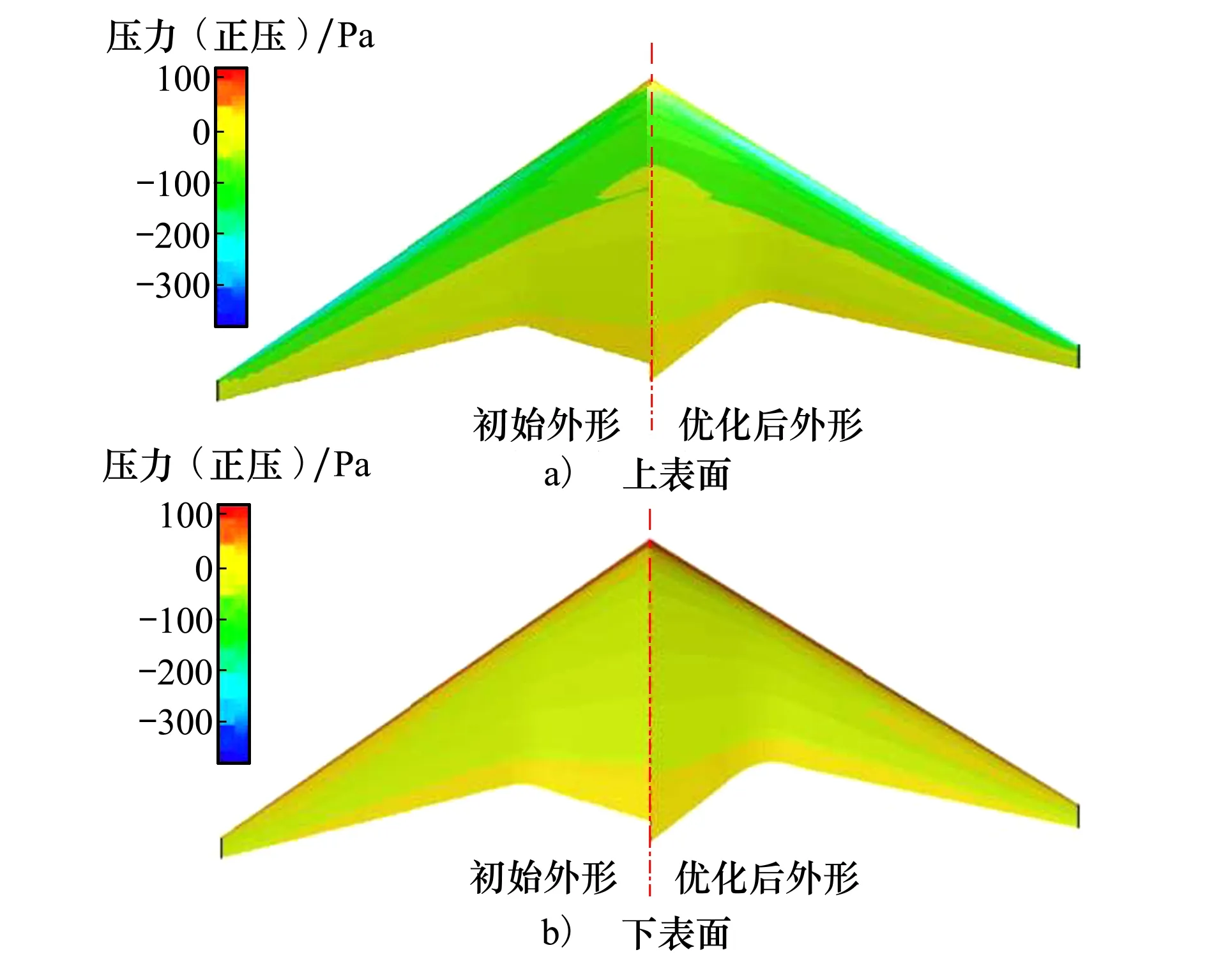
图10 优化前后表面压力对比

图11给出了优化前后BWBUG中纵剖面压力分布对比图，可以看出：优化后外形在艏部的压力波动明显小于初始外形；优化后外形在0.5Loa至尾部区域的下表面压力值大于初始外形，据伯努利方程可知该区域滑翔机表面的流体运动速度有所降低；因此，优化后滑翔机外形的黏压阻力和摩擦阻力均有所降低。

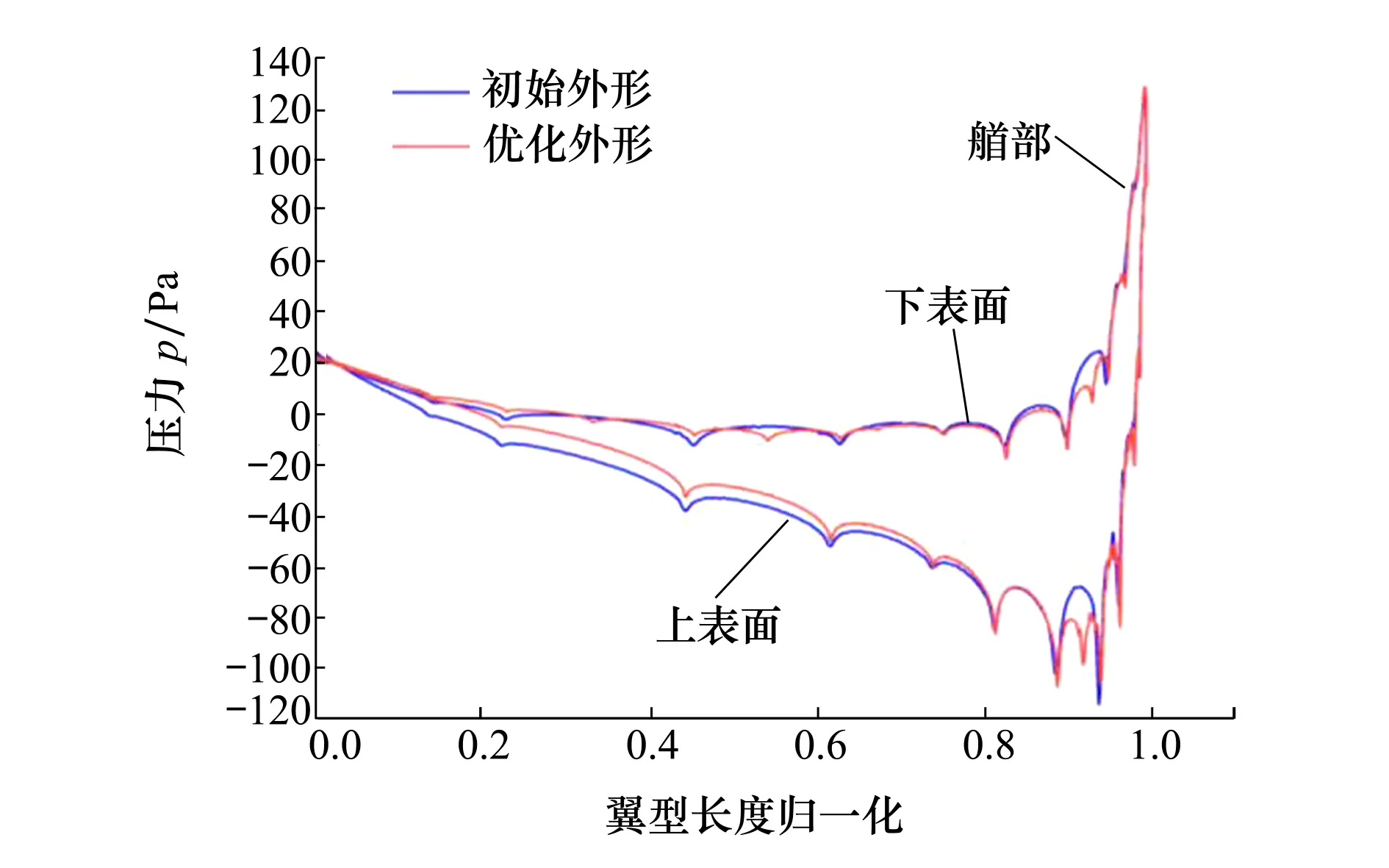
图11 中纵剖面压力分布图

图12给出了优化前后BWBUG外形沿翼展方向的归一化升力分布。由理论知：升力沿着翼展方向呈椭圆分布规律时，诱导阻力最小[3]。从图中可以看出，优化后外形的升力分布更接近椭圆分布，优化后外形诱导阻力小于初始外形。

图12 沿翼展方向位置升力分布图

由于BWBUG优化过程中，并未考虑滑翔机的稳定性，本文引用文献[4]中提出的水动力性能加权公式

(4)

式中：L,R和Mθ分别为滑翔机在α攻角下受到的升力、阻力和俯仰力矩；ω1和ω2为加权系数，因为BWBUG滑翔效率和运动稳定性2个要素同等重要。因此选取加权系数为ω1=0.5,ω2=0.5。根据(4)式计算出滑翔机外形优化前后水动力性能,如表5所示，从表5可以看出，优化后外形的升力系数提高了0.58%，阻力系数降低了10.22%，最大升阻比提高了12.01%，最佳升阻比对应最优攻角为6°，优化后模型的加权值提高了11.99%。以上数据表明，优化后的BWBUG流体动力性能具有显著提高。

文献[3]基于代理模型高维参数化方法，控制12个变量优化后翼身融合水下滑翔机的升阻比为17.46，本文采用组合优化方法控制6个变量优化后的升阻比为17.16，文献[3]所生成的样本数量远大于本文，但结果相当。

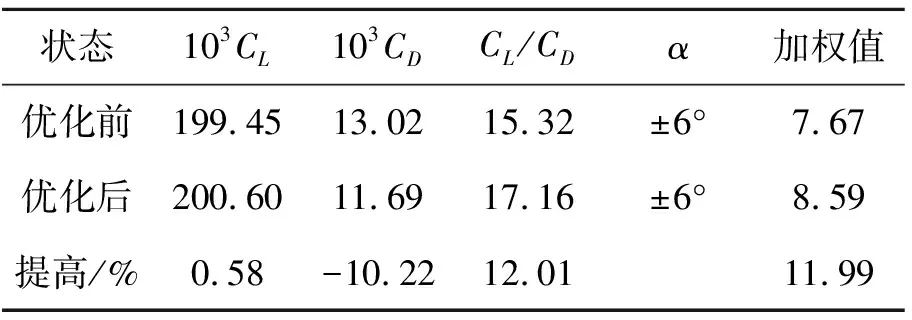
表5 优化结果

4 结 论

本文将先进的翼身融合布局引入滑翔机外形设计完成了滑翔机初始外形设计，采用NURBS曲线绘制BWBUG的精细参数化模型，采用组合优化算法，直接耦合调用黏流软件，完成了翼身融合滑翔机高升阻比的优化设计，给出了优化的滑翔机参数与构型，对比水动力性能指标优化后BWBUG均有显著提升，表明本文所建立的优化方法在滑翔机水动力优化领域具有一定的适用性。