基于深度强化学习的端到端无人机避障决策

张云燕, 魏瑶, 刘昊, 杨尧

(1.西北工业大学 电子信息学院, 陕西 西安 710072; 2.西北工业大学 航天学院, 陕西 西安 710072;3.西北工业大学 无人系统技术研究院, 陕西 西安 710072)

小型多旋翼无人机因为其体积小、动作灵活、适宜在复杂环境下完成机动，从而广泛应用于各种军用以及民用领域。科学技术的发展，也使得针对无人机的导航指导与控制技术得到了更大提升。然而，在陌生环境中实时进行自主导航却是极具挑战性的问题。在结构不能确定、光线条件多变的未知三维环境中，实现自主规避障碍物仍然是亟待解决的问题[1]。

传统的无人机避障算法[2-6]需要构建离线三维地图，在全局地图的基础上以障碍点为约束，采用路径搜索算法计算出最优路径。有的避障算法[7-8]虽然避免了繁杂的地图构建工作，但是需要手动调整大量的参数且机器人在避障的过程中不能利用避障经验进行自我迭代。随着机器学习的发展，研究人员将有监督学习引入无人机的避障之中，将避障看作是一个基于监督学习[9]的分类问题，但需要对每个样本标签进行标注，这样无疑费时费力。在无人机避障过程中，如何能够充分利用无人机三维空间信息，避免环境构建工作，简化算法模型，提升无人机自主避障能力以及无人机避障效率，最终实现无人机更加安全高效地到达指定目的地仍然是目前需要解决的问题。

随着机器学习的发展，强化学习[10]被科研人员应用于无人机的控制之中。强化学习主要通过与外界交互来优化自身的行为，它比传统机器学习更具优势：①训练前不需要对数据进行标注处理，能更有效地解决环境中存在的特殊情况；②可把整个系统作为一个整体，实现端到端输入输出，从而使其中的一些模块具有更强的鲁棒性；③强化学习与其他机器学习方法相比较更容易学习到一系列行为。 因此，使用强化学习算法的优势在于不依赖于传统非机器学习所需要的离线地图，以及监督学习所需要的人工标注的数据集，通过深度学习模型学习输入数据和输出动作的映射关系，使智能体具备处理高维连续空间下的决策问题的能力，避免复杂离线地图构建工作。

基于此，本文以三维环境下无人机避障问题为研究对象，研究了在含有建筑、树木、车辆等静态障碍物的陌生环境下，通过实时感知周围环境信息实现端到端的避障决策控制。本文的主要贡献在于：根据无人机探测能力、场景复杂度和障碍物的几何特性等因素，设计了 3DVFH[11]算法，利用无人机的探测视场角来约束速度范围，在三维环境内直接进行无人机路径规划，避免三维空间信息的缺失问题；针对3DVFH算法中速度控制不连续和速度方向选择受限的问题设计了DDPG[12]网络处理连续状态空间并输出连续控制变量。其中状态空间仅为深度图像数据和位置信息，易迁移至实际场景中，并且根据深度图像数据和无人机通过窗口定义价值函数提升算法收敛率，避免算法产生冗余陷入局部最优；最后，分别在仿真环境及实际环境中对2组避障算法进行测试。测试结果表明2组避障算法均可实现避障功能，并且DDPG算法优化了飞行轨迹，缩短了飞行距离，提高飞行的安全性，具有一定的应用价值。

1 算法原理

1.1 基于3DVFH的无人机避障

3DVFH算法由Vanneste等于2014年提出，该算法将二维向量场直方图应用于无人机三维飞行场景之中。算法假设无人机探测范围是以无人机中心为球心，直径为du的球面，以方位角α和俯仰角β作为横纵坐标，单位角δ为间隔，将球体内的障碍物信息转换为二值化的二维极坐标直方图，如图1所示，二值化结果用于判断区域能否通过。算法以与目标点夹角、最小避障角度以及与当前速度夹角作为权重，最终确定无人机避障方向。

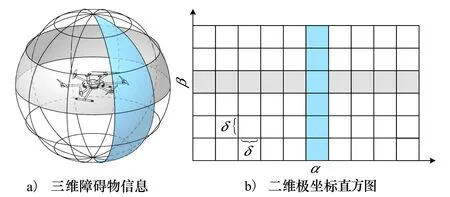
图1 二维极坐标直方图转换

3DVFH算法以栅格化的形式将无人机周围空间的障碍物信息进行降维处理，适合在复杂场景中应用，算法实现较为简单。但在实际应用中存在以下2个问题：

1) 根据3DVFH的原理和步骤可以看出，算法以建立在无人机中心的三维极坐标系为基础，输出下一步的运动方向，由当前运动姿态转换到该运动方向的线速度、角速度等这类动态信息均无法给出，速度连续性较差，会导致轨迹不够平滑，且难以进行轨迹优化。

2) 3DVFH使用了障碍物栅格相对无人机中心的方位来直接限定运动方向，使用了障碍物栅格距无人机中心的距离计算权重，间接反映距离对运动的影响程度。但由于极坐标直方图的二值化过程受阈值影响极大，会损失完整的距离信息。这导致阈值难以调参，使得无人机难以接近靠近障碍物的位置，因为这些方向被提前排除。减小直方图通过窗口可以在一定程度缓解该问题，但同时也会降低无人机避障安全性。

1.2 基于DDPG的无人机避障

为了解决1.1节中3DVFH算法使得无人机速度连续性差、避障轨迹不平滑问题，引入基于无人机视觉输入的、具有连续动作输出的深度强化学习方法来优化无人机避障轨迹，提高避障安全性。无人机的避障决策问题可以认为是在连续动作空间中的控制问题。DDPG采用了DQN(deep q-network深度Q网络)的思想和基于行动者-评论家[13](Actor-Critic)的算法结构，可以用来处理连续动作空间中的决策训练问题，其基于深度学习的部分使深度强化学习中的网络参数通过深度神经网络进行拟合与泛化，其策略梯度算法可以使智能体在连续的动作空间里依照学习结果选择合适的机动策略，并以确定性来避免策略梯度随机选择动作策略。

传统的DQN强化学习算法，尽管解决了高维的环境观察空间问题，却只能处理离散和低维的动作空间。因为它依赖于寻找使动作值函数最大化的动作，在连续值的情况下，需要在每一步进行迭代优化，从而导致离散动作数量爆炸。在连续的动作场景下，即需要智能体(无人机)的动作进行连续变化时，DDPG采用 Actor-Critic网络结构，并在Actor网络最后的输出层加入tanh激活层使得动作输出限制在[-1,1]之间，并根据需要进行缩放，保证输出为一个具体的浮点数，从而对智能体进行连续动作控制。在确定性策略的情况下没有概率的影响，当神经网络的参数固定下来的情况下，对于输入的同一个状态，必然只会输出同样的动作。

因此，本文将深度确定性策略梯度强化学习算法应用于无人机避障决策过程，以提高无人机动作连续性，平滑运动轨迹，实现避障决策优化。

1.2.1 DDPG算法原理

本文中，将无人机的观察信息即当前时刻无人机得到的深度图片以及无人机与目标之间的距离共同组合成为该时刻的状态信息st输入至神经网络。Actor网络根据无人机此时状态向无人机提供相应的动作at，无人机执行该动作与环境进行交互并根据此时得到的下一个状态s′获得奖励。无人机的目标便是通过学习最优策略π:S→A，来最大化累积折扣奖励Rt。

(1)

式中：rt为当前时刻无人机做出动作at与环境交互后得到的奖励值;γ为折扣因子。

DDPG采用具有连续动作空间的Actor-Critic网络结构，网络部分由Actor网络μ(s|θμ)、Actor网络对应的Actor目标网络μ′(s|θμ′)、Critic网络Q(s,a|θQ)、Critic网络对应的Critic目标网络Q′(s,a|θQ′)，其中θμ,θμ′,θQ,θQ′分别为对应网络的网络参数。

Critic网络根据当前状态动作来逼近计算动作极值函数，其更新方式与DQN相似，通过最小化损失函数学习最优动作价值函数。如公式(2)所示，为Critic网络的损失函数计算方法

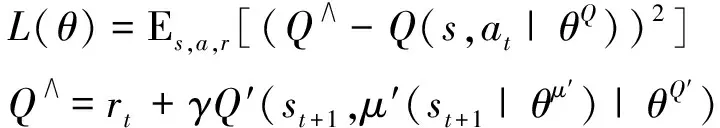
(2)

Actor网络确定性地将状态st映射到动作at,即基于当前环境状态给出无人机确定性动作策略。Actor网络依赖于Critic网络所给出的Q值估计，通过梯度上升对其网络参数θμ′进行更新。

为了避免自举算法过高估计价值函数，DDPG采用软目标更新策略，利用Actor目标网络μ′(s|θμ′)和Critic目标网络Q′(s,a|θQ′)来计算目标价值。Actor目标网络、Critic目标网络的更新方式为如公式(4)所示，其中τ为滑动平均系数，其取值通常小于1。

(4)

1.2.2 网络结构设计

DDPG所采用的Actor-Critic结构如图2所示，2个网络的交互过程为：智能体感知得到所处环境的状态信息，Actor网络根据此时的状态信息通过策略梯度计算出动作策略，智能体执行动作通过环境得到奖励以及下一个状态信息，该过程是与环境的一次完整交互过程。Critic网络根据奖励值计算当前状态、下一状态的动作价值函数并根据ΔTD error(ΔTD error为Critic网络所估计当前状态Q值与目标Q址网线所估计下一状态Q值之差)进行更新，然后行动者网络沿着最大化Critic网络计算的Q值方向进行更新。该网络结构能够在单步更新参数的同时控制连续变量，并借鉴了DQN算法的经验回放(experience replay)机制，从经验回放池中随机采样，打乱状态之间的相关性，加快收敛速度，提高数据利用率。

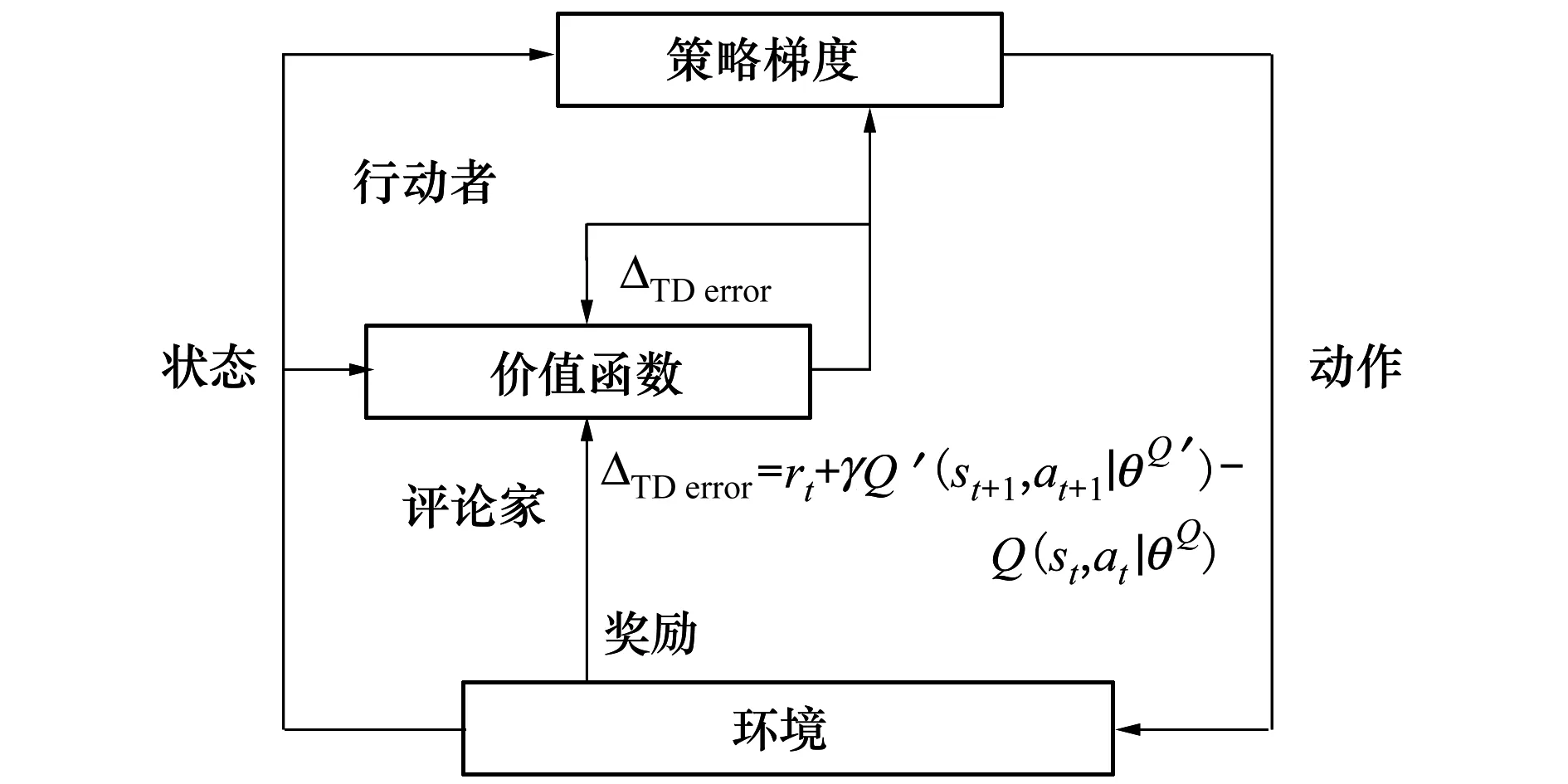
图2 Actor-Critic架构

本文采用的Actor和Critic网络具体结构如图3所示。Actor网络通过输入此时无人机状态信息 ，从而给出无人机基于该状态的动作 。其中Actor网络由2个全连接层搭建形成，每层神经元个数分别为300,600。各隐藏层间使用ReLU激活函数，输出层使用tanh激活函数规范无人机速度和旋转角速度，输出范围为(-1,1)从而保证输出的无人机动作为一个连续变化值。Actor目标网络结构与此相同。

Critic网络分为两部分，分别为对状态信息的处理以及对动作信息进行处理，输出为该时刻无人机的状态动作价值函数Q(st,at)，用来评价无人机基于此时状态给出动作的好坏。Q(st,at)动作价值函数越高表明在在该状态下Actor网络所选取的动作越好。其中状态信息st经过2个全连接层后得到特征，与动作at通过一个隐藏层后得到的特征逐级相加，通过最后的全连接层输出Q值。

整个DDPG算法网络结构如图4所示，DDPG算法包括4个网络，分别是Actor网络、Actor目标网络、Critic网络、Critic目标网络。其中Actor具体网络结构、Critic网络结构如图3a)～3b)所示，Actor目标网络、Critic目标网络分别与Actor网络、Critic网络结构保持一致，但网络参数由超参数τ和Actor网络、Critic网络参数共同实现更新。

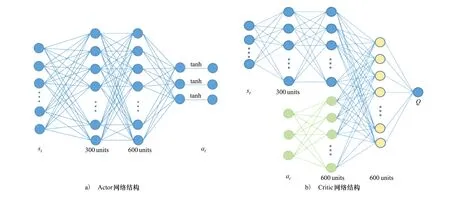
图3 Actor-Critic结构图

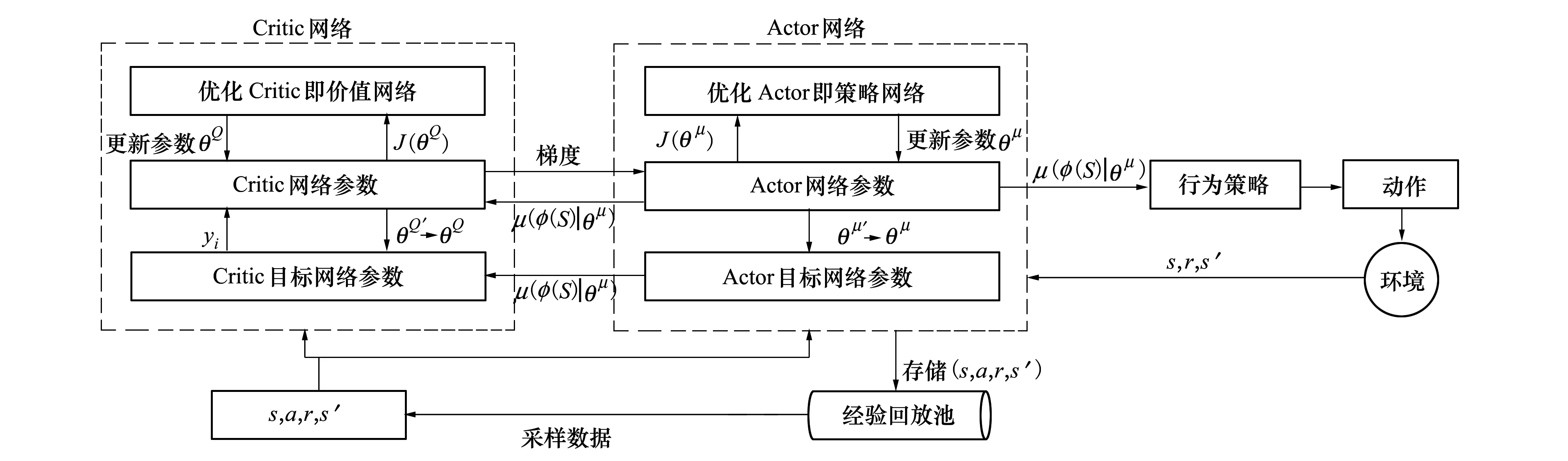
图4 DDPG算法结构图

·Actor网络：基于目前的状态s选择合适的动作a，更新策略网络参数θμ，从而生成与环境相关的(s′,r)；

·Actor目标网络：基于从经验池中抽取的下一个状态s′，选择下一个合适的动作a′并保证其为最优，θμ′则每隔一段时间从θμ更新；

·Critic网络：负责价值网络参数θQ的迭代更新，负责计算当前Q值Q(s,a|θQ)。对于第i次迭代，目标Q值Q∧=r+rQ′(s′,a′|θQ′)；

·Critic目标网络：负责计算目标Q值中的Q′(s′,a′|θQ′)部分。网络参数θQ′定期从θQ复制。

1.2.3 DDPG算法设计

1) 图像预处理

本文选用深度摄像机成像分辨率为640×480，FOV约为80°×60°，取特征向量大小为16×16，去除图像边缘八像素宽度以定位图像中心，并将深度图像缩放处理，最终得到39×29分辨率的处理后图像(如图 5所示)，其单个像素对应2°×2°的视场角。为保留距无人机最近的障碍物信息，每个像素点灰度取缩小前对应区域内的最小值。

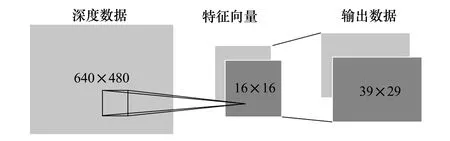
图5 深度图像处理示意图

深度摄像机的有效探测范围为10 m，取7 m为避障响应距离，该距离对应灰度值约为178。图像二值化过程与3DVFH算法一致，对于处理后图像，灰度值低于178的像素点Hb=1，高于178的像素点Hb=0。

对于通过窗口的确定，根据本文所选无人机尺寸和深度探测范围，选择距无人机中心7 m，宽×高为2 m×1 m的区域作为通过窗口范围，根据视场角换算并缩小处理，得到像素大小约为9×5的区域，如图6所示。

图6 图像处理结果

2) 状态空间建模

状态空间S中包含了环境中智能体的属性和信息, 并以此为依据来选取要执行的动作。为了实现无人机的避障，需要获取的信息分别为：无人机采集得到深度图像二值化结果Hb(i,j)、与目标点的距离Dt{dx,dy,dz}和碰撞标记Scol，具体内容见表1。

表1 状态空间表

3) 动作空间设计

DDPG算法可以处理动作连续情况下的决策问题，此处选择无人机的2个状态：速度v(m/s)以及偏航角速度ωz(rad/s)作为主要动作，以避免利用位置信息需要全局定位的问题，具体内容见表2。在此，把速度和角速度进行映射处理，再进行计算，使它们的值更适用于神经网络。

表2 动作空间表

4) 奖励函数设计

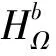
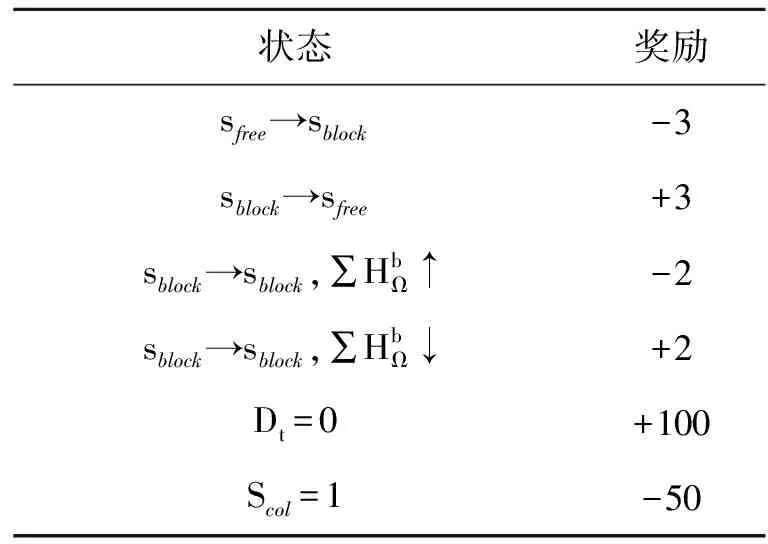
表3 奖励函数表

1.2.4 算法实现步骤

算法实现步骤如下：

输入：Actor网络、Actor目标网络、Critic网络、Critic目标网络参数(θμ，θμ′,θQ,θQ ′),折扣因子γ、软更新系数τ、批量梯度下降的样本数m、目标网络参数更新频率C、最大迭代次数T、随机噪声函数N。

输出：最优Actor网络参数θμ，Critic网络参数θQ。

步骤1 随机初始化θμ,θQ′=θQ,θQ,θμ′=θμ。清空经验回放集合D；

步骤2 对i从1到T，循环执行以下步骤：

①初始化S为当前状态序列的第一个状态，得到其特征向量φ(S)。

②在Actor网络基于状态S得到动作A=μ(φ(S)|θμ)+N。

③执行动作A，得到新状态S′，奖励R，终止状态标志is-end。

④将五元组{φ(S),A,R,φ(S′),is-end}存入经验回放集合D。

⑤令S=S′。

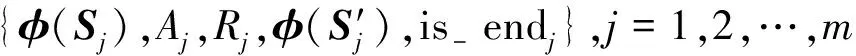
⑦更新Critic网络参数θQ。

⑧更新Actor网络参数θμ。

⑨若T%C=1(表明此时C能够被T整除，网络按照该频率更新Critic目标网络和Actor目标网络参数)，更新Critic目标网络和Actor目标网络参数。

⑩若S′为终止状态，本轮循环结束，否则转到步骤②继续训练。

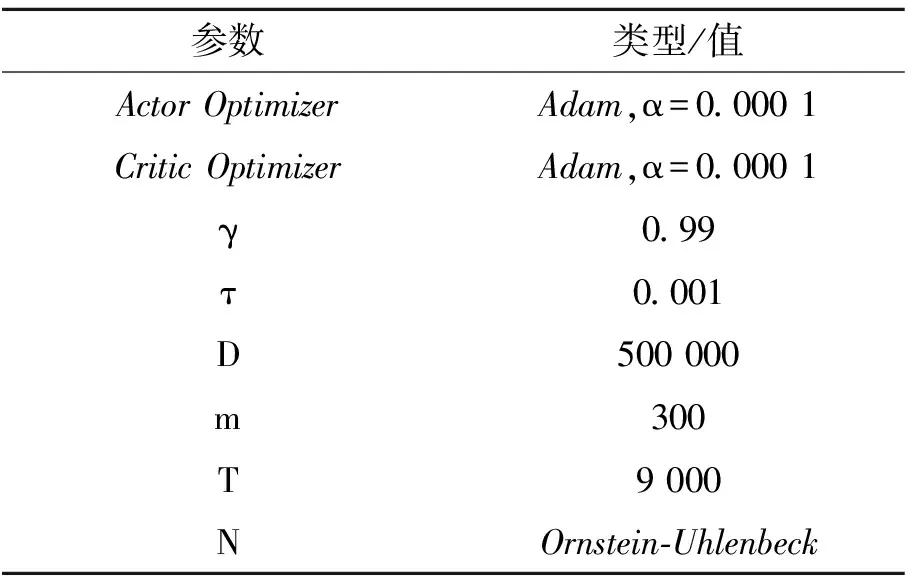
表4 参数配置表

2 仿真及实验研究

2.1 仿真实验场景

微软公司开源了一个用于无人机模拟测试的高仿真软件AirSim[14]。该软件依赖于虚幻引擎可以提供逼真的测试场景，并模拟其动力传感(如图7所示)。AirSim支持开源和跨平台开发，因此本文选用AirSim作为仿真系统的基础，开展无人机避障算法研究。

图7 AirSim仿真效果图

仿真场景试验在仿真计算机中完成,计算机软件配置：Window10CUDA10.1,tensorflow2.3.0,Python3.7。

仿真场景的复杂度较高，俯视图方向能较为直观地展现无人机飞行轨迹(图8为本次仿真场景左透视图)。同时为保留障碍物高度信息，本文对仿真场景俯视图进行深度化处理，令障碍物高度对应障碍物投影的灰度值，灰度值越低，表示障碍物越高，效果如图9b)所示。同时，为提升DDPG算法训练速度，将仿真场景约束为图9a)所示的100m×100m范围内，当无人机飞出该范围视为发生碰撞。

图8 仿真场景左透视图

图9 俯视图处理效果

2.2 仿真场景测试

DDPG的算法实验过程如图10所示，当无人机获取的深度图像信息为图10b)时，经由算法处理得到的二值化极性直方图为图10c)，根据当前速度方向对应的通过窗口区域进行奖励函数区域计算。对于图10c)的二值化结果，若当前速度指向正前方，则当前深度图像代表状态的奖励由图10d)的红框区域确定，此时，无人机处于sfree状态。

图10 DDPG算法状态奖励计算过程

无人机训练过程如图11所示，其中Cumreward为每一训练回合的累积奖励值，Meanreward为趋势线，表明每十个回合奖励值的平均值拟合曲线。本次训练共计9 000次，从图中可以看出随着训练次数增加，累积奖励和平均奖励都在逐渐增加，并且保持相对稳定。在前2 000次训练过程中，无人机处于探索状态因此其平均奖励均小于0，但随着后期神经网络开始训练，其累积奖励在逐步提升并保持在100左右附近，表明此时无人机已经能够躲避障碍物并且安全到达指定地点。需要注意的是，可能在训练过程中出现无人机无法到达目标点的现象，由于无人机的探索率是随着训练次数递减的，因此，该现象是正常的，并不影响最终无人机躲避障碍物到达指定目标点的能力。并且由于探索阶段无人机只进行探索，其对应的神经网络并不进行梯度更新，此时网络输出的策略动作可能会在相邻的2个控制周期内出现突变。自由探索阶段是为了将更多的训练信息存入经验回放池中，从而保证在后续的网络训练阶段，神经网络可以更快学习得到好的策略。此时的动作突变并不会对无人机的训练产生影响。当神经网络开始训练时，Actor网络会沿着使Critic网络给出更高Q值的方向进行梯度更新。随着网络的训练收敛，策略所输出动作在2个相邻的控制周期中出现突变的可能性会越来越小。在神经网络参数固定情况下，对于输入的同一个状态，必然只会输出同样的动作，在相邻的2个周期内所输出的动作便不会发生异常突变。

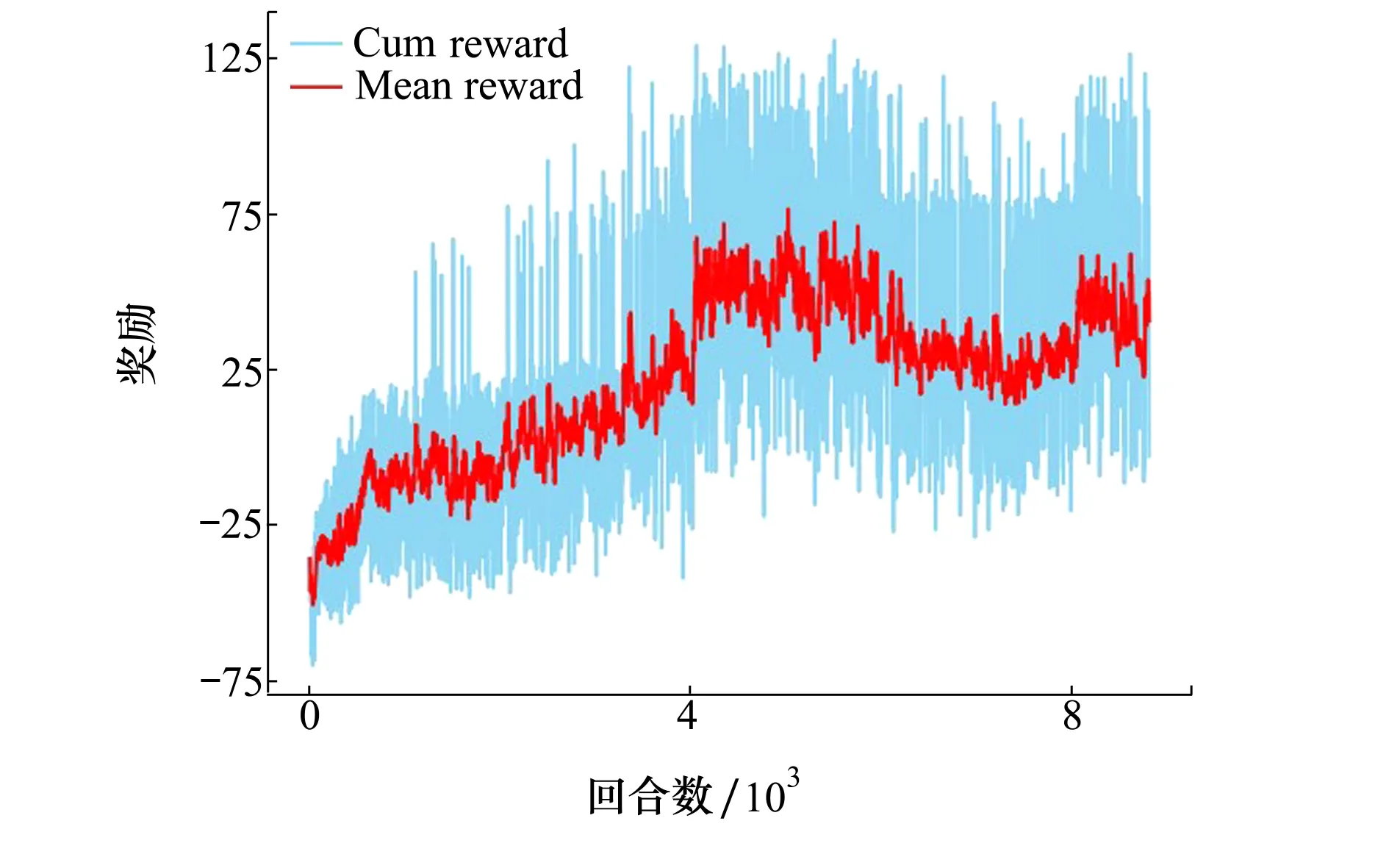
图11 DDPG算法训练过程

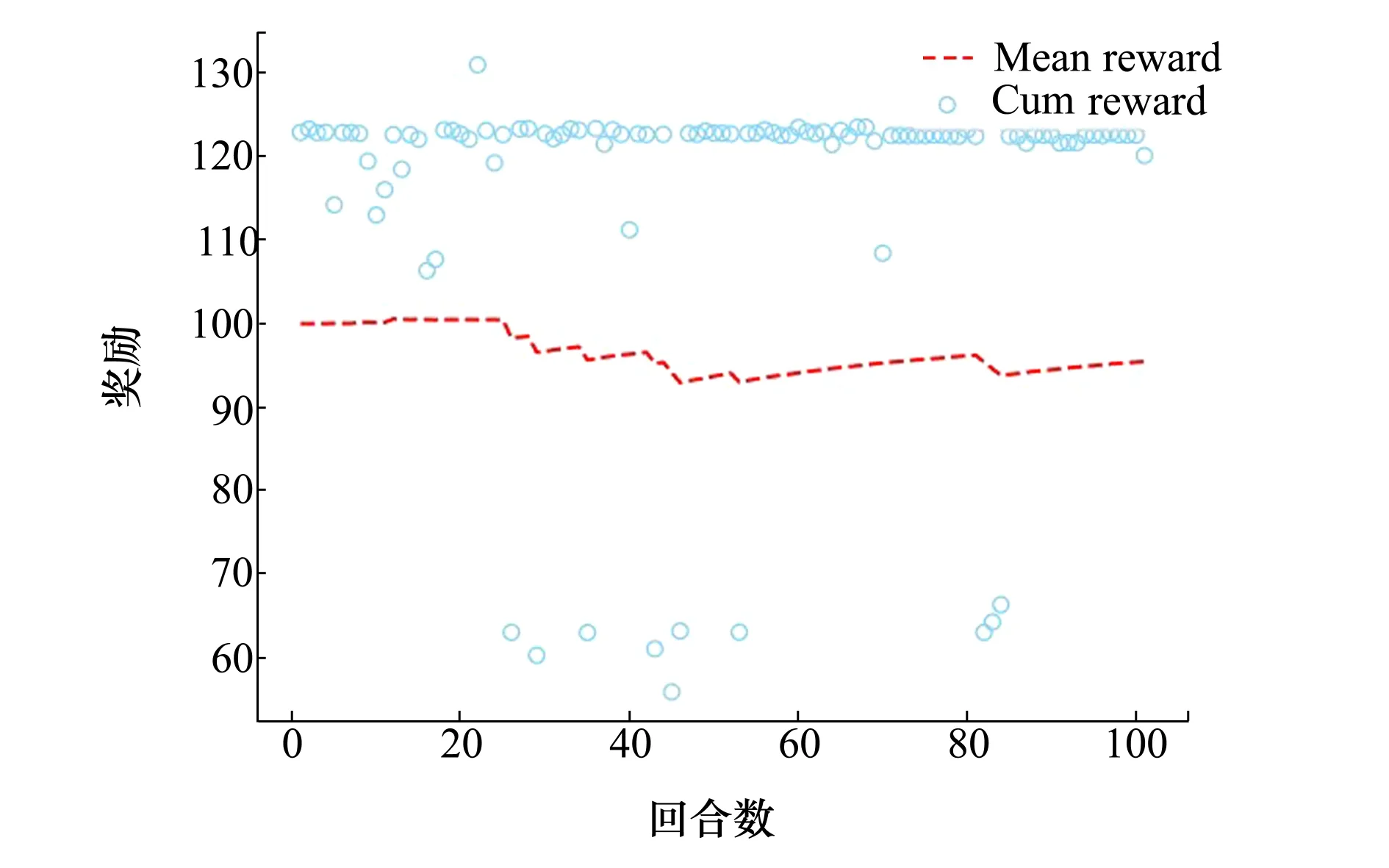
图12 DDPG算法测试结果

为更好地展现所提出的算法性能，首先将训练得到的算法在同样的环境下进行了100次测试，测试结果如图 12所示。由于奖励函数设置为当无人机产生碰撞时奖励值为-50，因此当累积奖励大于0时表明无人机均可以躲避掉障碍物。当无人机的累积奖励值大于100时表明此时无人机能够躲避掉所有障碍物并到达指定位置。综上所述，在100次测试结果中，有90次均为成功，无人机躲避障碍物成功率高达90%，同时本次测试的平均奖励值为95。

在此基础上，将DDPG算法在测试环境中无人机的运动轨迹与基于3DVFH的避障算法在同样的仿真场景中轨迹进行对比，2种算法试验结果的俯视图如图13所示。2种算法起始点与目标点位置设置相同，各试验5次，其中，图13a)为DDPG算法9 000次迭代后效果。对比结果明显展现出DDPG算法飞行轨迹的平滑度高于3DVFH算法，这同时缩短了飞行距离，提高了避障效率。

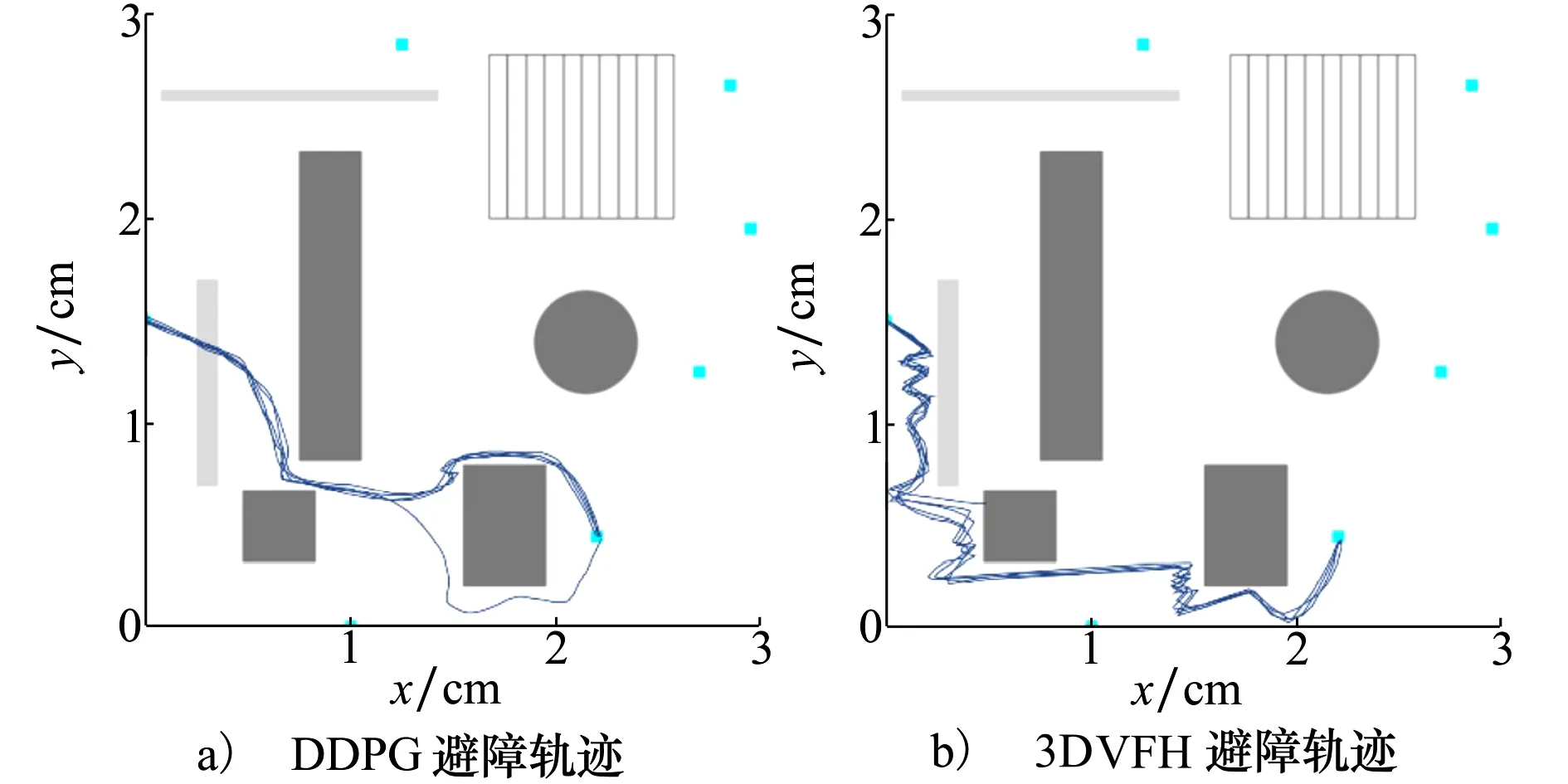
图13 仿真结果对比

2.3 真实场景测试

针对无人机避障需求，本文确定以“大疆M600pro六旋翼无人机+RealSenseD435i深度摄像机+妙算Manifold2机载计算机”组合成完整硬件系统进行试验测试。其中试验无人机和深度摄像机如分别图14～15所示。

图14 试验所用无人机 图15 Intel D435i 深度摄像头

在真实场景试验前，为了保证测试效果，提高试验安全性，需完成以下几个步骤：首先，测试无人机飞控在Onboard模式下的坐标系及飞行速度误差，以修正算法的控制效果，提高控制精度，缩小控制效果与仿真场景的差异；其次，确定结合RealSenseD435i深度摄像机实测时的试验保险措施。真实环境往往比仿真环境更为复杂，当传感器发生异常，输出错误的探测信息可能导致无人机发生撞击。应设置紧急悬停功能防止这类事故发生；最后，将避障系统与无人机平台相结合，观察算法在实际飞行中的过程，并进行适当调整，以达到预期效果。

2.3.1 3DVFH算法实际验证

在实测环境中，无人机根据3DVFH算法实现避障的过程如图16所示。由于3DVFH算法对速度控制的不连续性，因此当避开障碍物后，速度的突变会导致无人机产生摆动，表现为图16d)～16e)过程。从图16a)～16f)为发现障碍物、调整前进方向以躲避障碍物并最终避开障碍物的部分过程。

图16 3DVFH算法实际避障过程

2.3.2DDPG算法实际验证

经过实测表明本文所设计算法其网络计算效率满足实时控制要求，避障算法生成避障控制指令的控制周期为55ms。图17为在实测环境中，无人机根据DDPG算法实现避障的过程。在DDPG算法中，无人机避障时所采取的避障策略均来自仿真环境的训练结果。在该算法中，可明显看出当发现障碍物时，无人机会放慢前进速度进行避障，当避开障碍物后继续高速向前飞行。图17a)～17f)为发现障碍物、调整前进方向以躲避障碍物并最终避开障碍物的部分过程。

图17 DDPG算法实际避障过程

2.3.3 试验结果对比

为直观展现2种算法在实测中的效果，试验设置了高空无人机视角拍摄完整飞行过程，2种算法的避障过程如图18所示。试验表明，网络的计算效率满足实际控制要求。其中，蓝色为3DVFH算法飞行轨迹，在避障结束段有明显摆动痕迹；红色为DDPG算法飞行轨迹，整体较为平滑。

图18 高空视角下的无人机避障过程

3 结 论

本文以无人机在未知三维环境中对静态障碍物的智能规避为研究背景，使用六旋翼无人机，在无全局地图信息的条件下，采用深度图像感知方案，对无人机避障硬件平台、无人机避障仿真系统、深度强化学习避障算法和传统无人机避障算法进行了研究。

本文根据无人机探测能力、场景复杂度和障碍物的几何特性等因素，结合无人机探测视场角约束速度范围设计了3DVFH算法，在三维环境直接进行无人机路径规划。针对3DVFH这类传统算法速度连续性差、避障轨迹不平滑问题本文引入深度强化学习中的DDPG算法，建立了基于DDPG算法的端到端决策控制模型。通过训练表明，在进行了4 000个episode后算法收敛,无人机学习得到了避障能力。在此基础上，将训练收敛的DDPG算法模型在仿真环境中进行测试，测试表明无人机躲避障碍物成功率高达90%。

分别将3DVFH算法和DDPG算法避障轨迹在仿真环境和实际环境中进行测试，实践表明3DVFH算法在避障结束阶段有明显摆动痕迹，DDPG算法优化平滑了飞行轨迹，缩短了飞行距离，提高飞行的安全性，具有一定的应用价值。