紧密编队飞行的建模控制与仿真
郑锐平, 史静平, 屈晓波
(1.西北工业大学 自动化学院, 陕西 西安 710129; 2.陕西省飞行控制与仿真技术重点实验室, 陕西 西安 710129)
近距离编队飞行的概念起源于候鸟[1]。研究表明,编队飞行有利于鸟类节省能量,提高飞行耐力[2-4]。自20世纪70年代以来,许多学者和机构一直在研究飞机编队。NASA研究中心在风洞实验中使用了2架F-18C模型[5]。结果表明,与前机相比,后机的阻力降低了25%,油耗降低了18%。大量学者对飞机[6]进行了风洞实验研究。在分析和模拟尾流涡旋运动和衰减[7]方面做了大量的工作。
为了共同防御和集中火力,许多高速军用飞机在执行任务时通常以低速度进行近距离编队飞行。这也有节省燃料的效果,从而增加射程[8]。1998年,美国宇航局兰利研究中心在海洋上空对一架巡航四引擎涡轮螺旋桨飞机进行了一系列测试[9]。2002年,Ray等[10]使用飞行测试技术来评估编队飞行的性能优势。关于尾流模型,2014年Ahmad等[11]对Lamb-Oseen、Burnham-Hallock和Proctor 3种飞机尾流模型的性能进行了评述。
编队飞行的研究主要基于模型分析和风洞实验,难度较大。对于一些小型无人机来说,进行风洞实验显然是不经济的,而随着计算机的快速发展,CFD逐渐成为与风洞实验相辅相成、相互验证的重要设计方法,并在航空领域得到了广泛的应用。本文针对实验室的具体飞翼飞机,进行了双机编队的CFD计算,并使用CFD软件Xflow进行计算分析。通过与可用的实验数据对比[7,9,12-13],验证了计算结果的正确性。了解紧密编队飞行的空气动力学特性,对于确定2架飞机的最佳相对位置、分析长机[14]的尾涡对僚机的气动影响具有重要意义。针对无人机的非线性模型,设计了紧密编队的控制律,使僚机能够相对于长机精确地跟踪到适当的位置。通过数字仿真验证了控制律的准确性。
1 诱导涡空气动力学模型
如图1所示,所研究的无人机为XQ7B。长机与僚机的紧密编队可以用3个相对坐标来表示:纵向距离lx、横向距离ly和垂直距离lz。
建立尾涡数学模型的第一步是诱导尾流风速的计算。长机产生了2个翼尖涡(右和左)[15],这些翼尖涡总是与长机速度方向一致,而在僚机任意点的诱导速度都垂直于各自翼尖涡的涡线[16]。在紧密编队飞行中,纵向距离lx对诱导力和力矩的影响远小于横向距离ly和垂直距离lz[17]。因此,在本文中,忽略了lx对尾涡的影响。

图1 编队飞行示意图
首先建立诱导速度VΓ(d)的模型,通过研究诱导速度的分布来建立编队飞行的涡模型,如公式(1)所示。

(1)
式中:Γd为涡强度;d为测量点到涡线的垂直距离;rc为涡核半径。
在此设置两机的纵向距离大于2倍展长,僚机处于长机的近场尾涡延伸区内,翼尖涡在完成卷起之后相当长的一段时间内旋转速度稳定,设置公式(1)中的β1=0,β2=π,得到公式(2)

(2)
涡核半径用rc表示,d表示该点到涡核的距离[18],涡流强度Γ通过公式(3)计算

(3)
式中:CLL为长机的升力系数;S是机翼面积;b是机翼展长。僚机的机翼总诱导速度为
w(s)=wl(s)+wr(s)
(4)
式中:w表示总诱导速度;wl表示左机翼产生的诱导速度,wr表示右机翼产生的诱导速度。
其中wl和wr分别通过公式(5)和(6)计算

(5)

(6)
最后,可以计算出僚机机翼的平均上洗速度和侧洗速度。无人机的参数如表1所示。

表1 无人机的参数
诱导升力系数如图3~4所示。ΔCL是左右对称的,因此, 对于每个纵向距离ly,就有2个最优的位置。诱导升力系数在ly=-0.125bm,lz=0 m位置处最大。

图2 诱导升力系数(三维视图)

图3 诱导升力系数(俯视图)
2 CFD计算
2.1 CFD软件设置
本文使用的CFD计算软件是Xflow。它是Next Limit Technology开发的新一代计算流体动力学仿真软件。该方法基于无网格、拉格朗日粒子法和大涡模拟技术。通过设置粒子的密度,模拟真实的大气环境,省去了传统CFD软件划分网格的时间,既能真实地分析复杂的几何和运动物体,又大大提高了流体计算的效率和水平。设置简单,操作速度快。
Xflow的基本参数设置及颗粒密度图如表2、图4~5所示。

表2 Xflow参数设置

图4 远场粒子的分布 图5 近场粒子的分布
2.2 计算模型
在本文的编队计算中,长机与僚机采用同一模型,均为飞翼模型。飞翼模型的3个视图如图6所示。
本文中,采用的长机和僚机均为同型号并且飞机的气动特性完全对称,长机左右两侧的诱导速度对称分布,本文中编队时,将僚机放在长机的左侧。为了更好地确定长机与僚机之间的位置关系,首先定义位置坐标的零点,长机的头部定义为x坐标的零点,当长机的左翼翼尖与僚机的右翼翼尖距离为0时,为y坐标的原点,当长机机翼高度与僚机机翼高度相同时,就是z坐标的原点,僚机后退、向左、向上运动时为坐标系的正方向。

图6 飞机的三视图
长机和僚机的迎角相同且同时变化,每次变化2°,变化范围是2°~12°。长机的位置坐标是固定的,坐标是:x=0 m,y=0 m,z=0 m。僚机的位置坐标是x=0.698 m,z=0 m;在每个迎角下,僚机的y坐标从y=-0.174 5 m变化到y=0.349 m,每次变化0.125b。
3 CFD计算结果分析
从计算结果可以看出,飞机编队飞行时的气动特性随两机相对位置变化。
3.1 飞机迎角对编队的影响
僚机和长机的高度保持相同,长机和僚机初始迎角都为0°,两机的迎角每次同时增加2°,然后测量僚机的升力系数,如图7所示,当僚机的右翼尖与长机的左翼尖之间的距离是(-0.25b,-0.125b,0,0.125b,0.25b,0.375b,0.5b)时,能看到僚机的升力系数明显大于单机的升力系数。由图8可知,当飞机迎角为6°时,僚机升阻比最大。由图9可知,当僚机y方向坐标为-0.125b时,长机对僚机的影响最大,俯仰力矩系数提升最明显,从阻力系数变化图10中可以看出,在任何位置和迎角下,僚机的阻力系数均小于单机时的阻力系数,由此可见编队飞行可以有效减少僚机飞行时遇到的阻力。

图7 升力系数 图8 升阻比系数 图9 俯仰力矩系数

图10 阻力系数
3.2 垂直距离对编队的影响
为了研究前后机垂直间距对编队飞行的影响,将前后机的攻角固定为2°。飞机的位置如图11所示。当2架飞机在垂直方向上的距离较大,编队飞行时,僚机没有气动收益。如图12所示,可以看出,当2架飞机在相同高度时,僚机受到的诱导升力最大。当z/b=0.0,y/b=-0.125时,僚机的升阻比最大。这与图2~3的结果一致。
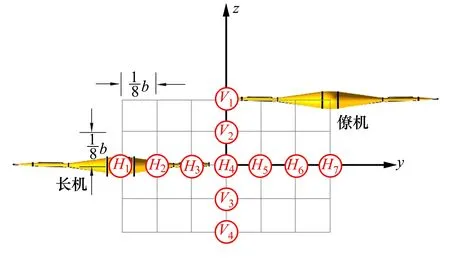
图11 两机垂直间距示意图(正面图)
当僚机的右机翼尖与长机左机翼尖重叠时,长机引起的诱导尾流会减弱僚机机翼引起的下洗作用,从而有利于僚机飞行。

图12 升阻比的增量随z的变化 图13 俯仰力矩系数的增量随z变化 图14 滚动力矩增量随z变化
力矩系数的增量如图13~14所示,这些影响对评估飞机飞行稳定性至关重要。图13显示了在横向和垂直方向上,长机和僚机的相对位置发生变化时,俯仰力矩的增量。图14为滚动力矩的变化情况。
4 编队飞行控制器的设计
本节设计了紧密编队控制器的外回路控制律,在这个模型中,飞行的内环控制器已经设计好并且是稳定的。

图15 紧密编队飞行控制器
如图15所示,本文重点研究了非线性外环控制器的设计。长机的状态量表示为[xl,yl,zl,vl,γl,χl]T,将这些状态量输入给图15中的“规划模块”,代入Δx,Δy,Δz计算出僚机在惯性坐标系中的期望位置和状态量[xd,yd,zd,vd,γd,χd]T。结合紧密编队耦合效应,建立了僚机的动力学模型,紧密编队几何队形参数为Δx=2b,Δy=-0.125b,Δz=0。控制器的目的是使僚机跟踪长机,处于期望的位置,使位置跟踪误差为零。因此,引入以下位置跟踪误差

(7)

(8)
保持公式(8)的稳定,期望的速度V和航迹倾斜角γ在公式(9)中给出

(9)
航向角通过公式(10)计算。

(10)
紧密编队飞行控制器如图16所示,并且在MATLAB′s SIMULINK中进行了仿真验证,其中的增益值为Kx=-0.3,Ky=-0.1,Kz=-0.035。

图16 编队飞行轨迹
如图16~19所示,僚机刚开始远离长机,能够很快地收敛于期望的位置。所设计的控制器能够使僚机快速准确地到达期望位置,并且保持紧密编队队形。

图17 不同时刻飞行器相对位置

图18 无人机由远到近紧密编队轨迹

图19 无人机状态仿真图
5 结 论
本文利用CFD软件对双机编队飞行进行了计算。研究了僚机在长机翼尖涡影响下的气动特性。设计了一种小型飞翼无人机的紧密编队飞行控制系统。设计的编队飞行控制器使僚机能够准确地跟踪长机。因此,研究的紧密编队飞行控制器可以充分利用气动耦合效应引起的减阻效应,这将减少编队的燃料消耗,并加大编队的航程。

