模糊推理下多模型融合的异步测距定位算法

向英杰，魏连锁，谢思雅，马敬云，孙明

模糊推理下多模型融合的异步测距定位算法

向英杰，魏连锁，谢思雅，马敬云，孙明

（齐齐哈尔大学 计算机与控制工程学院，黑龙江 齐齐哈尔 161006）

针对水下节点随着洋流运动具有移动性特性，导致现有水下测距定位算法存在定位精度低、抗干扰能力差等问题．对此，提出一种模糊推理下多模型融合的异步定位算法．首先采用深海拉格朗日洋流模型描述水下节点运动规律，模拟节点运动速度，构建锚节点与待定位节点信息动态交互模型．在此基础上，构建基于信号传播时延（Round-trip Time，RTT）与接收信号强度（Received Signal Strength Indication，RSSI）动态定位模型，再引入波动系数作为调节因子，利用模糊推理规则建立RTT与RSSI相融合的动态定位模型，提出模糊推理下多模型融合的异步测距定位算法．仿真实验表明，改进算法与对比算法相比，考虑了水下节点的移动性，降低了水声信道的不稳定性对定位精度的影响，定位误差降低了25.58%，抗干扰能力显著提高．

水下传感器网络；模糊推理；多模型融合；异步定位

海洋是21世纪最具有探索意义的领域，也是未来世界各国竞争的核心地方[1]，它拥有大量的资源，可以为人类提供生存与发展的新空间．对海洋资源的开发与利用离不开水下无线传感器网络（Underwater Wireless Sensor Networks，UWSNs），UWSNs是由各种各样的传感器节点组成，具有自组织性、可靠性高等特点[2]．人类对海洋资源的探索也是依靠这个网络，在UWSNs基础研究中，水下节点定位起着举足轻重的作用，不但为节点感知数据提供重要的位置信息，也为水下目标跟踪提供位置依据[3]．和地面传感器网络相比，水下节点定位主要面临２方面的挑战[4]：（1）水下传感器节点会随着洋流移动，若定位算法未考虑节点的移动性则会增加定位误差；（2）水下传感器节点间只能通过水声信道进行数据传输，因此，水下传感器节点间的通信时延较大，且受海洋复杂环境的影响，定位的精度和可靠性会降低．

现有UWSNs节点定位算法中，根据距离测量可分为基于免测距定位[5-6]和测距定位[7-11]算法，免测距与测距结合的定位算法[12]，而水下异步定位是测距定位算法研究的热点．Yeredor[13]提出了使用协作节点进行节点定位，该方法解决了异步时钟下精度差的问题，但其鲁棒性较差，复杂度高，容易受海洋复杂环境的影响．Canclini[14]等为了解决上述问题，提出为每个传感器节点选择可行的到达时间差关系，利用几何考虑和总体广义互相关系（GCC）形状的表征，设计了一种复杂度低和鲁棒性强的算法．Carroll[15]等又针对其能量消耗大的问题，提出了按需请求的异步定位算法，但其抗干扰的能力差．孙彦龙[16]基于文献[15]的算法提出了具有抗干扰能力的异步定位算法．该算法变相使用了RTT与RSSI测距技术，消除了节点间时钟异步的影响，但其未考虑节点的移动性对定位误差的影响，且抗干扰能力较差．

因此，本文采用拉格朗日洋流模型描述节点运动规律，模拟节点运动速度，构建锚节点与待定位节点信息动态交互模型，对基于信号传播时延与信号强度2个定位算法进行动态修正，再引入波动系数作为调节因子，利用三角棣属度函数，构建模糊推理下RTT与RSSI融合定位模型，从而设计出一个定位精度高，抗干扰能力强的水下传感器网络异步定位算法．

1 模型构建

1.1 洋流模型

虽然水下环境十分复杂，但水下物体运动并不是完全无规律的，而是呈现出半周期的运动特性，在水下无线传感器网络中，水下传感器节点会随着洋流一起运动，其运动特征在时间与空间上呈现相关性．因此，本文考虑利用洋流模型来描述节点的运动情况．

在文献[17]中提出一种权威的洋流模型，本文用此模型模拟节点的运动态势

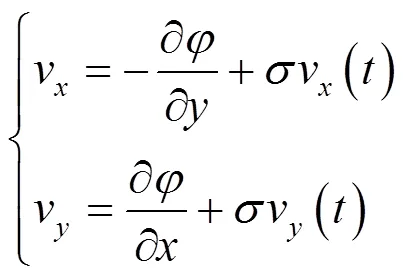
1.2 移动节点位置信息交互过程

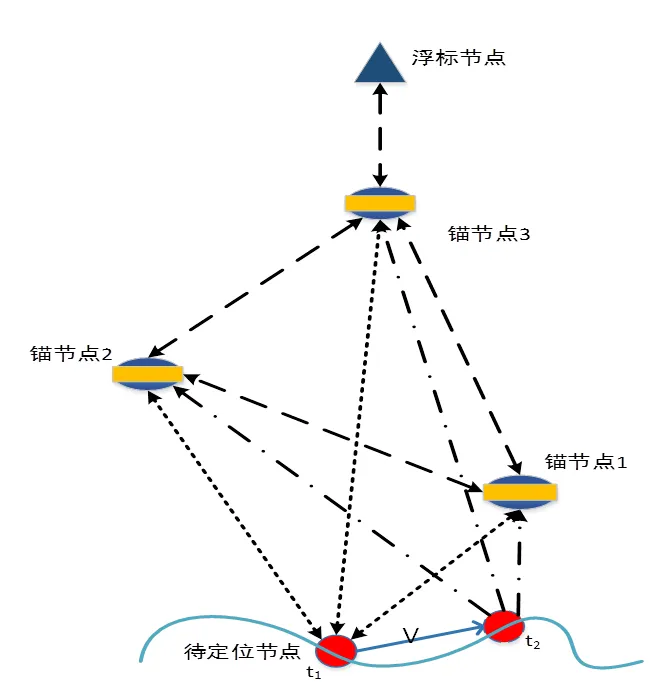
图1 待定位节点位置变化

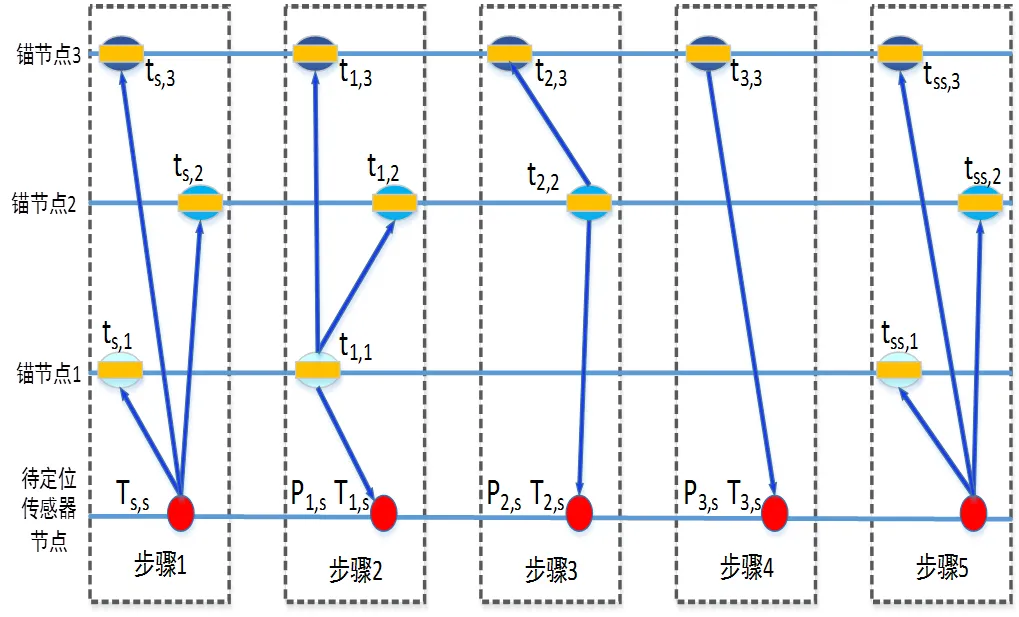
图2 定位过程中的信息交互过程

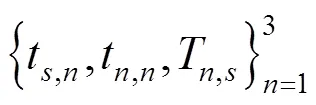
1.3 基于传播时延（RTT）的动态定位模型

基于信号传播时延的定位算法中水下传感器网络节点使用的异步时钟模型为

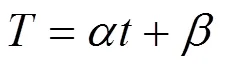
1.4 基于接收信号强度（RSSI）的动态定位模型

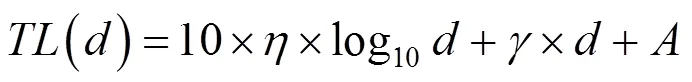
式中：右侧第1项为传播损失，柱面传播时为2，球面传播时为1；右侧第2项为衰减损失；右侧第3项是其他原因引起的传播损耗，如多径传播损耗，这个值可以认为是5～10 dB的一个常数．

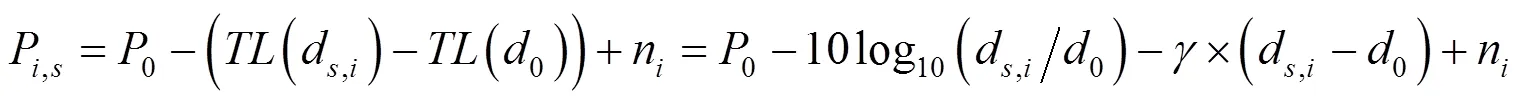
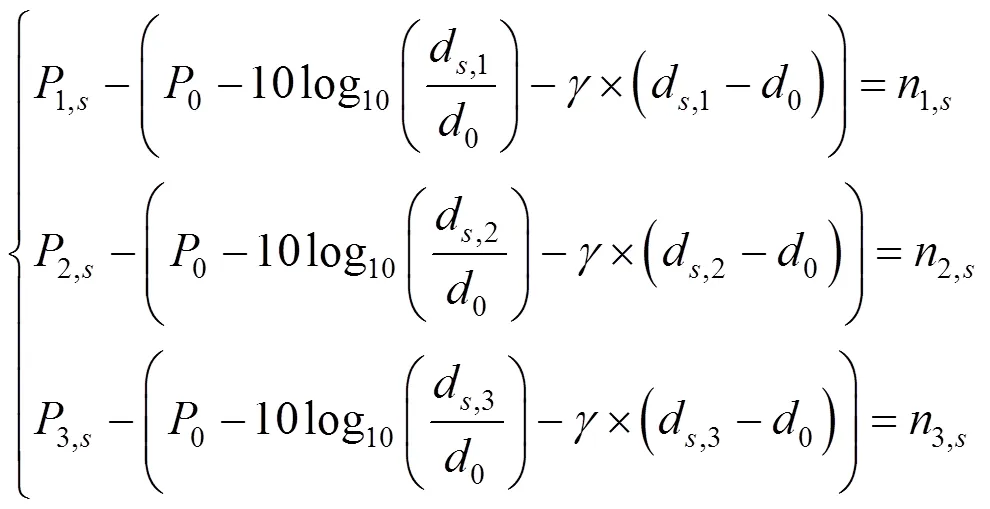
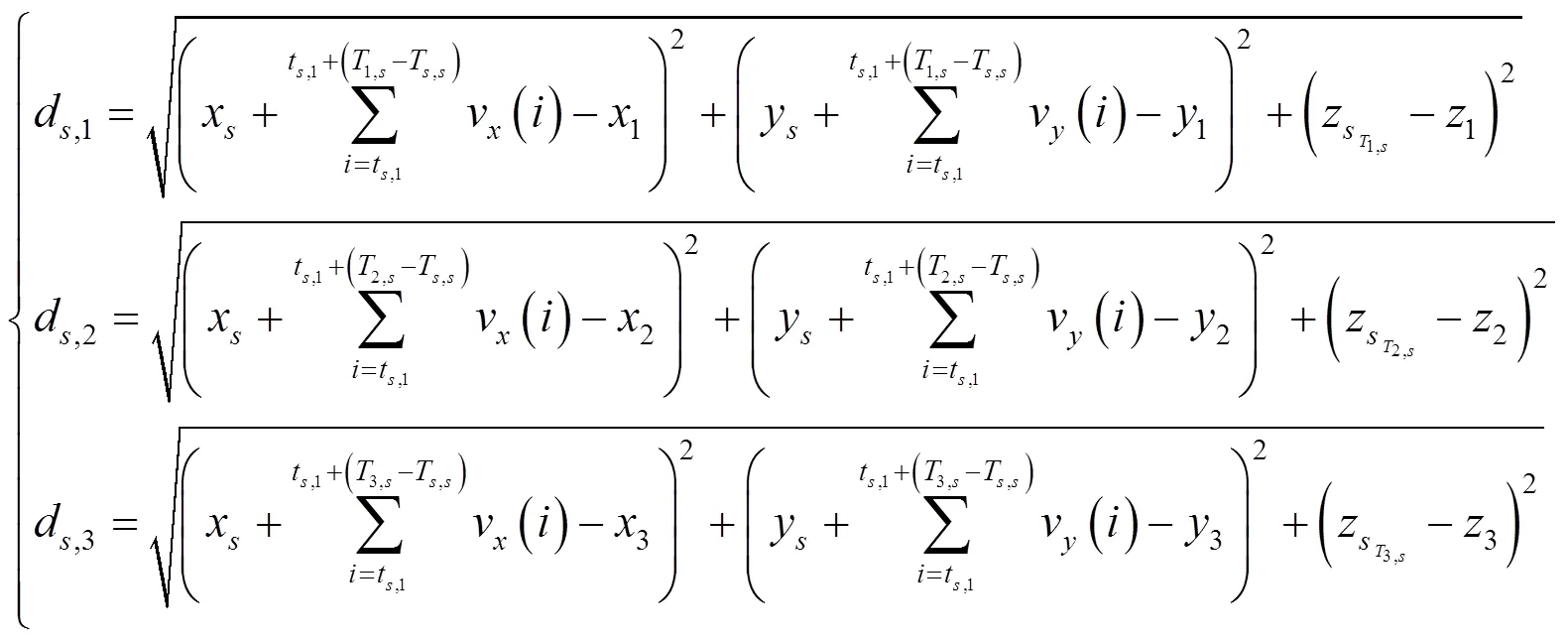
则使所有误差值之和最小的待定位传感器节点位置最优估计函数为

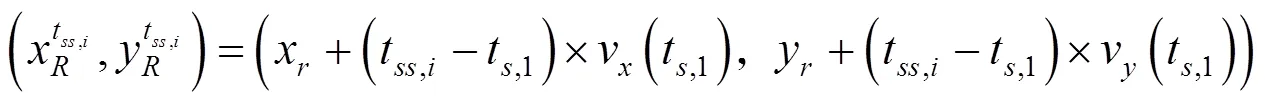
2 模糊推理下TDOA与RSSI融合定位模型

基于信号传播时延与基于接收信号强度的测量方法可分别得到一个估算位置，在一般情况下基于信号传播时延的方法得到的估算位置精度较高，基于接收信号强度的方法得到的估算位置精度较低．但在实际的测量场景中，人为的攻击，环境的强干扰，设备时钟的不稳定都会造成时间测量出现错误[18]，从而造成水下待定位传感器节点使用基于信号传播时延的算法定位结果出现较大误差．由于接收信号强度值的获取方法是对一个时间段内的信号强度进行连续采样后取均值，因此，通过权重系数将２种算法得到的估算位置进行融合就能增强定位算法的鲁棒性．根据洋流模型可知水下传感器节点的速率变化规律，本文提出了一种自适应的权重动态调整算法．

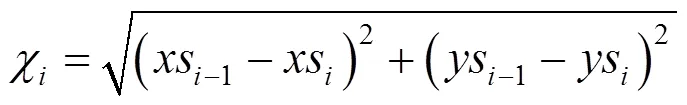
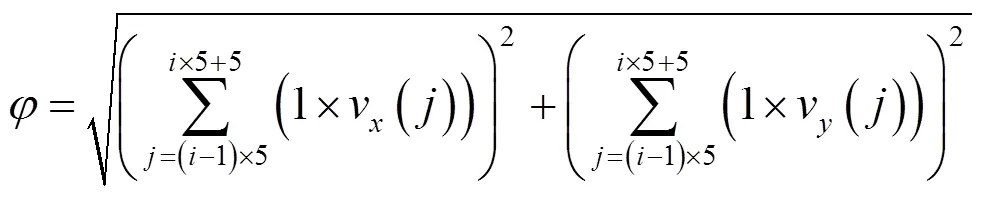
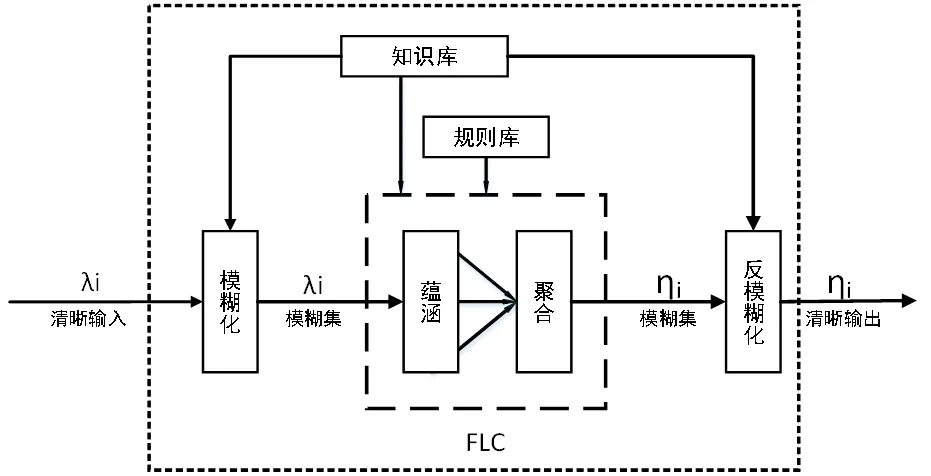
图3 模糊推理下RTT与RSSI融合定位模型

模糊推理下RTT与RSSI融合定位模型见图3．主要包括3个步骤：

（1）模糊化：利用输入棣属度函数将清晰的数字输入转换为模糊集的过程．本文采用三角棣属度函数

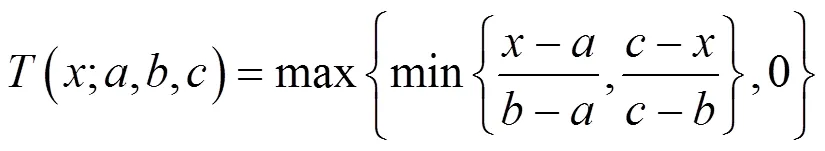
式（16）为其三角函数式，其中：代表三角函数曲线与横坐标的2个交点值；代表曲线顶点的横坐标对应的值．和分别有各自的三角棣属度函数（见图4），这些棣属度函数储存在知识库中．输入与输出的模糊集都使用小小（Small Small，SS），小（Small，S），中（Middle，M），大（Large，L），大大（Large Large，LL）5个语言变量来标记．和的论域均为[0，1]．

（2）模糊推理：在模糊化后，模糊推理使用知识库和规则库将输入模糊集映射到输出模糊集．规则库是基于实验与经验建立的规则表，自适应权重因子调整算法的规则见表1．模糊推理的过程有２步，第１步蕴涵，从规则表中找到与输入的模糊集对应的所有规则；第２步聚合，通过取最大值的方法将所有选择的输出模糊集聚合成一个输出模糊集．

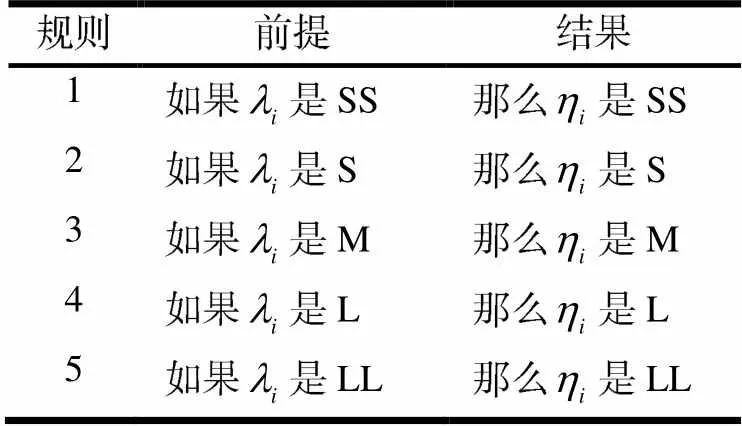
表1 模糊推理规则表

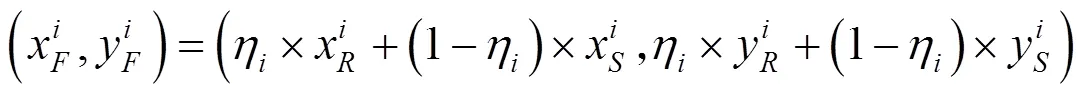
3 模糊推理下多模型融合的异步定位算法

本文提出的模糊推理下多模型融合的异步定位算法（Localization of Multi-Model Fusion under Fuzzy Reasoning，FR-LOMMF）分为3个步骤：

4 仿真分析

4.1 算法时间复杂度分析

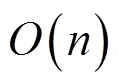
4.2 定位误差分析

截取不同信号传播时延噪声方差下相同10个时间点上的定位数据（见图5），RTT随方差增大定位误差逐渐增大，RSSI误差则相对稳定在4 m上下波动，而ABWF与FR-LOMMF介于2种算法之间，且FR-LOMMF更接近于RTT，误差更小．由此可知，在没有出现时间测量错误的情况下，4种算法都能很好地完成10次定位任务，说明了４种定位算法的有效性，也能直观地展现出４种算法的定位精度．且由于FR-LOMMF每次定位均独立进行，由RTT与RSSI动态融合所得，所以不会出现误差积累，误差不会随时间出现变大现象．

图5 不同信号传播时延噪声方差下的定位误差

4.3 抗干扰性分析

截取相同的10个时间点（见图6），在截取的第3个和第8个时间点上加入了错误的时间测量．RTT在这２处时间点上都出现了大的偏差，也就是如果在出现大偏差时权重值选取不当将存在较大的风险，在图6中，FR-LOMMF展现出了更强的抗干扰能力．

时间测量错误时（见图7），在第3个时间点和第8个时间点RTT分别出现了13 m和17 m的定位误差，而RSSI使用的是一段时间内的信号强度连续采样后的平均值，因此该算法定位表现不受影响．FR-LOMMF在RTT出现较大误差时依然能维持在一个较低的误差范围，相较之下，比ABWF的抗干扰能力有极大的提高．

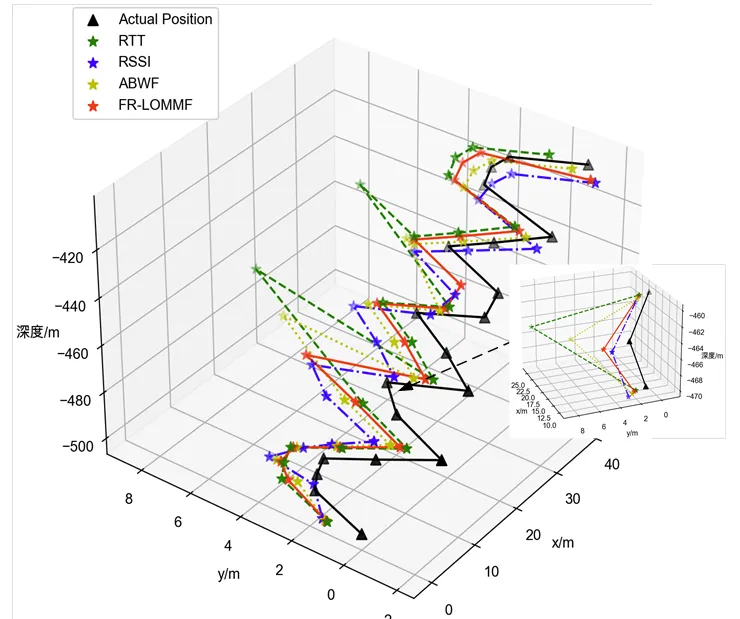
图6 时间测量出现错误４种算法的定位情况

图7 时间测量出现错误的情况下水下节点的定位误差

4.4 定位精度随锚节点密度变化分析

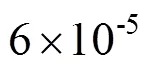
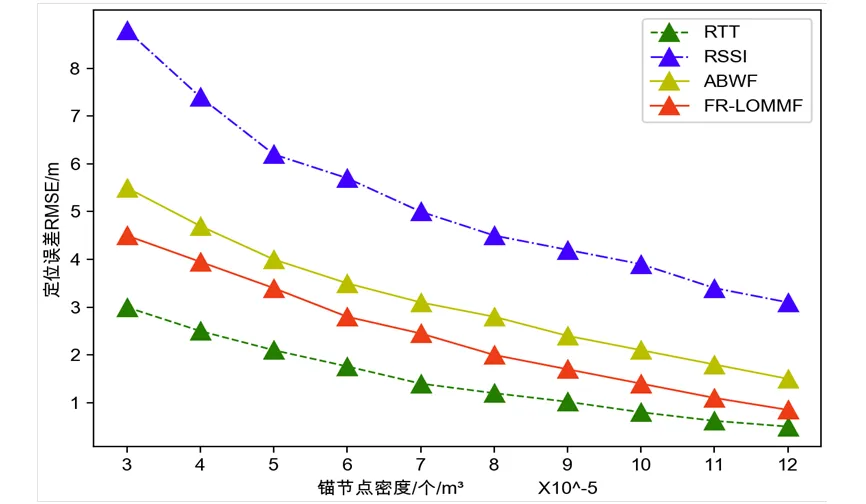
图8 定位精度随锚节点密度变化分析

5 结语

针对现有水下节点异步定位算法未考虑节点的移动性导致定位误差大，抗干扰能力差等问题，在深海拉格朗日洋流模型基础上，利用模糊推理规则，构建了RTT与RSSI融合动态定位模型，进而提出了一种模糊推理下多模型融合的异步测距定位算法（FR-LOMMF）．仿真实验表明，本文提出的算法比传统的算法定位误差更低，且在时间测量出现错误时具有较好的抗干扰能力．

虽然该算法降低了定位误差，提高了抗干扰能力，但由于水下环境复杂，声速和锚节点速度是变化的，本文只考虑了存在误差的情况下如何进行求解，并没有对误差进行建模得到较好的估算．因此，后续的工作将着眼于误差建模研究．

[1] 李晋，姜晓轶．助力海洋强国建设：海洋信息互联互通、深度融合、智慧应用：2018中国海洋信息技术高端论坛会议综述[J]．海洋信息，2018，33（3）：5．

[2] Tuna G．A survey on deployment techniques，localization algorithms，and research challenges for underwater acoustic sensor networks[J]．International Journal of Communication Systems，2017，30（17）：12-13．

[3] ErolKantarci M，Mouftah HT，Oktug S．A survey of architectures and localization techniques for underwater acoustic sensor networks[J]．IEEE Communications Surveys and Tutorials，2011，13（3）：487-502．

[4] Tan H P，DiamantＲ，Seah WKG．A survey of techniques and challenges in underwater localization[J]．Ocean Engineering，2011，38（14）：1663-1676．

[5] HAN G，JIANG J，ZHANG C，et al．A survey on mobile anchor node assisted localization in wireless sensor networks[J]．IEEE Communications Surveys and Tutorials，2016，18（3）：2220-2243．

[6] 王采薇，杜秀娟．水下无线传感器网络节点定位的定点神经网络算法研究[J]．信息技术与信息化，2020（5）：231-233．

[7] Le TK，Ono N．Closed-form and near closed-form solutions for TDOA-based joint source and sensor localization[J]．IEEE Transactions on Signal Processing，2017，65（5）：1207-1221．

[8] HU Y，Leus G．Robust differential received signal strength-based localization[J]．IEEE Transactions on Signal Processing，2017，65（12）：3261-3276．

[9] WANG Y，HO D．Unified near-field and far-field localization for AOA and hybrid AOA-TDOA positionings[J]．IEEE Transactions on Wireless Communications，2017，17（2）：1242-1254．

[10] ZHANG B，WANG H，ZHENG L，et al．Joint synchronization and localization for underwater sensor networks considering stratification effect[J]．IEEE Access，2017，5：26932-26943．

[11] YANG M，Jackson D R，CHEN J，et al．A TDOA localization method for non-line-of-sight scenarios[J]．IEEE Transactions on Wireless Communications，2019，67（4）：2666-2676．

[12] 王鑫，田艺，蒋华，等．基于锚节点移动路径动态规划的定位算法[J]．计算机工程与设计，2020，41（8）：6．

[13] Yeredor A．Cooperative self-localization in asynchronous sensors networks based on TOA from transmission at unknown locations//[C]．InProceedings of IEEE International Conference on Acoustic，Speech and SignalProcessing，Brisbane，QLD，Australia，2015：2844-2848．

[14] Canclini A，Bestagini P，Antonacci F，et al．A robust and low-complexity source localization algorithm for asynchronous distributed microphone networks[J]．IEEE/ACM Transactions onAudio，Speech，and Language Processing，2015，23（10）： 1563-1575．

[15] Carroll P，Mahmood K，Zhou S，et al．On-demand asynchronous localization for underwater sensor networks[J]．IEEE Transac-tions on Signal Processing，2014，62（13）：3337-3348．

[16] 孙彦龙．水下无线传感器网络中节点定位与目标跟踪算法研究[D]．秦皇岛：燕山大学，2019．

[17] Leif E A，Francesco S，Lars I．An iceberg forecast approach based on a statistical ocean current model[J]．Cold Regions Science and Technology，2018：5-9．

[18] WANG Y，MA X，Leus G．Robust time-based localization for asynchronous networks[J]．IEEE Transactions on Signal Processing，2011，59（9）：4397-4410．

Multi-model fusion clock asynchronous range location algorithm based on fuzzy reasoning

XIANG Yingjie，WEI Liansuo，XIE Siya，MA Jingyun，SUN Ming

（School of Computer and Control Engineering，Qiqihar University，Qiqihar 161006，China）

Due to the mobile characteristics of underwater nodes moving with ocean currents，the existing underwater ranging and positioning algorithms have some problems such as low positioning accuracy and poor anti-jamming ability．To solve these problems，proposes an multi-model fusion clock asynchronous range location algorithm based on fuzzy reasoning．Firstly，use the deep sea Lagrange current model to describe the motion law of underwater nodes，simulate the motion speed of nodes．Then，build the dynamic interaction model of anchor nodes and unlocated nodes．On this basis，build a dynamic positioning model based on round-trip time（RTT）and received signal strength indentation（RSSI），and then import the fluctuation coefficient as the regulating factor．Based on fuzzy reasoning rules，the dynamic clock location model of RTT and RSSI fusion is established，and then propose the multi-model fusion clock asynchronous range location algorithm based on fuzzy reasoning．Simulation experiments show，compared with the comparison algorithm，the improved algorithm proposed takes the mobility of underwater nodes into consideration，reduces the influence of the instability of underwater acoustic channel on the positioning accuracy，reduces the positioning error by 25.58% and significantly improves the anti-interference ability．

underwater sensor network；fuzzy reasoning；multi-model fusion；asynchronous positioning

1007-9831（2022）10-0036-08

TP393

A

10.3969/j.issn.1007-9831.2022.10.008

2022-05-17

向英杰（1997-），男，四川南充人，在读硕士研究生，从事水下传感器研究．E-mail：790135337@qq.com

魏连锁（1975-），男，黑龙江齐齐哈尔人，教授，从事水下传感器研究．E-mail：451118227@qq.com