仰角对海上浮式风机系统流体动力性能影响研究
韩长志,陈淑玲,杨 帅,许思乾
(江苏科技大学,江苏 镇江 212003)
从“十二五”到“十四五”,国家风电发展政策逐渐向海上发电倾斜。2020 年,我国海上风电累计装机约900 万千瓦,其中新增装机达到306 万千瓦。随着我国风电技术的日渐成熟,风电的深水化、大功率化已成为必然的发展趋势。为保证风机的运行及降低建造成本,基础的形式也由传统的固定式向漂浮式发展。在水深大于80~100 m 海域,相对于固定式基础,浮式基础无论经济效益还是安全性能,都处于领先地位。但是浮式风机铺设海域的海况更加复杂,更易受到大波浪的影响,从而其稳定性、可靠性和生存能力相对于浅海固定式风机更具挑战性。
近年来,依靠计算流体力学(Computational Fluid Dynamics,CFD)方法,越来越多的学者对浮式风机系统进行耦合数值研究。万德成等[1]基于开源软件OpenFOAM 开发了用于风机气动模拟的nao-FOAM-SJTU 求解器,对浮式风机系统的气—水动力全耦合模型进行了数值分析。TRAN T T 等[2]对DeepCWind 半潜浮式风机平台分别用CFD 方法和势流方法进行研究,分析了不同湍流模型对自由衰减运动的影响,并对时间步长和网格数量进行了收敛性验证。RODDIER D 等[3]采用数值分析和模型试验相结合的方法对风机进行了水动力分析,其中水动力分析采用TIMEFLOAT,伺服弹性计算软件FAST 与TIMEFLOAT 耦合计算平台运动和风力机载荷。为了验证FOWT 动力学仿真程序的准确性,开展了OC3 和OC4 项目,对不同海上结构的模拟响应进行代码比对[4-6]。KOO B J 等[7]开发了自己的代码MLTSIMFAST,以分析OC4 半潜式风力发电机,并将其数值结果与DeepCwind 模型试验结果进行比较。KIM H C 等[8]利用FAST-CHARM3D 时域全耦合动力分析程序,对5 MW OC4 FOWT 在有或无定常、动力风的随机波浪中进行了数值模拟。REN N等[9]使用FLUENT 分析了波浪—风耦合条件下的5 MW 张力平台型风机,并将模拟结果与试验数据进行了验证。ZHANG Y 等[10]使用商业计算流体力学软件STAR-CCM+,对DeepCWind 半潜式浮动平台与美国国家可再生能源实验室(National Renewable Energy Laboratory,NREL) 5MW 风力发电机模型在风浪联合激励环境条件下进行了完全耦合的动态分析。TRAN T T 等[11]使用动态流体相互作用(Dynamic Fluid Body Interaction,DFBI) 方法和风浪激励条件下的重叠网格技术对一个OC4 半潜式FOWT进行建模,发现CFD 结果和FAST 数据之间有很好的整体一致性,两个方法都使用了准静态方法对系泊线进行建模。COULLING A J 等[12]使用DeepCWind半潜浮式平台结合5 MW 风机进行了模型试验,同时将试验结果与FAST 计算结果对比,结果表明FAST 在耦合的浮式风力机动力学上能够获取到许多相关的物理现象。此外,提出了FAST 和试验过程的差距和改进方案,以确保浮动风机系统的精确数值建模。LIANG L 等[13]使用MATLAB 编写了用于海上浮式风力发电机动态模拟的空气—水动力耦合计算代码,其中水动力是基于势流理论模拟,且通过试验方法进行验证。BENITZ M A 等[14]进一步对半潜浮式平台的六自由度体运动进行模拟,并与DeepCwind 项目的试验结果进行全面比较。YU Z Y等[15]使用qaleFoam 混合模型[16-17]计算分析了风机叶片气动载荷、支撑平台水动力特性和尾迹区流场信息的耦合效应。结果表明,该混合模型可以很好地用于FOWT 耦合建模计算。YAN X K 等[18]对带有NREL 5 MW 风机的半潜式DeepCwind 平台设计了相应的系泊系统,然后在AQWA-OrcaFlex-FAST 中建立了完全耦合的空气—水—伺服弹性模型,分析和比较了均匀风和动态风对平台运动、系泊系统的有效张力、叶片变形和塔架受力的影响。此外,为了验证具有冗余设计的系泊系统的可行性和安全性,对系泊系统的影响进行了分析。
本文首先利用计算流体学软件STAR-CCM+对10 MW 风机和OC4-DeepCWind 5 MW 半潜浮式平台分别进行气动力和水动力性能的数值验证。根据计算结果,进一步对OC4-DeepCWind 10 MW 半潜浮式风机系统耦合动力性能开展数值研究,计算了不同叶轮俯仰角对浮式风机系统发电效率及平台运动响应的影响。
1 数值模型
1.1 CFD 数值方法
本文基于CFD 技术研究风浪联合作用下海上浮式风机系统的流体动力性能。在笛卡尔坐标系下,对于连续、不可压缩、非定常流体的连续性方程和N-S 方程如下。

式中,Gk表示由速度梯度引起的湍动能生成项;Gω表示ω 方程生成项;Γk和Γω表示k 和ω 的有效扩散项;Yk和Yω表示由于湍流运动引起的和的耗散项。
自由液面的捕捉采用流体体积法(Volume of Fluid,VOF),该方法引入流体体积分数α,α 表示一个单元格内某种流体所占比例,本次计算中的取值如下[21]。

1.2 网格生成技术
本文使用滑移网格技术和重叠网格技术分别模拟风机旋转和浮式风机系统运动。
重叠网格也称作“嵌套”网格,用于以任意方式相互重叠的多个不同网格的计算区域,因此可以良好处理相互独立网格之间产生的无约束位移运动[21]。任何涉及重叠网格区域的研究都具有封闭整个求解域的背景区域,以及包含域中的体的一个或更多较小区域,如图1 所示。

图1 重叠区域示意图
在重叠网格中,网格单元分组为活动、不活动或受体网格单元。在活动网格单元中,将对离散控制方程进行求解。在不活动网格单元中,不会对任何方程进行求解,但是如果重叠区域在移动,这些网格单元可以变为活动状态。
滑移网格技术具体来说,整个计算区域分为两个子区域。叶片区域周围的网格随叶片移动,并与叶片保持相对静止,而其他区域保持静止状态。它只需要处理局部网格的整体运动和界面的插值。它不涉及网格的变形和重叠网格,从而节省了计算时间和计算机内存[22]。
1.3 动态流体相互作用
使用DFBI 模块模拟刚性物体在流体域中压力和剪切力作用下的运动,并考虑系泊线的恢复力。STAR-CCM+通过计算由于各种影响作用在物体上的合力和力矩,进而求解刚体运动的控制方程,以确定刚体的位置变化。图2 显示了说明DFBI 方法的工作流程图。

图2 DFBI 工作流程
2 建模及数值验证
本节使用STAR-CCM+软件建立数值风洞和数值水池模型,分别对实际尺寸风机和半潜浮式风机系统开展气动性能和水动力性能分析,完成对STAR-CCM+软件数值建模的可靠性验证。
2.1 模型参数
2.1.1 风机参数
本风机叶片源自丹麦科技大学(Technical University of Denmark)设计的DTU 10 MW 风机[23]发电机叶片模型,如图3 所示,风轮直径178 m,叶片数量3 片,符合我们数值耦合研究的尺寸和要求。具体风机参数如表1 所示。

图3 DTU 10 MW 风机模型

表1 风机模型参数
2.1.2 半潜浮式平台参数
本文釆用美国国家可再生能源实验室设计的5 MW OC4-DeepCwind 半潜浮式平台对数值水池进行验证工作[12],采用10 MW OC4-DeepCwind 半潜浮式平台进行半潜浮式风机系统的耦合计算工作。半潜浮式平台各部分结构是通过桁架结构进行刚性连接,风机由中部立柱支撑。按照表2 模型参数建立图4 所示OC4-DeepCwind 半潜浮式平台模型。
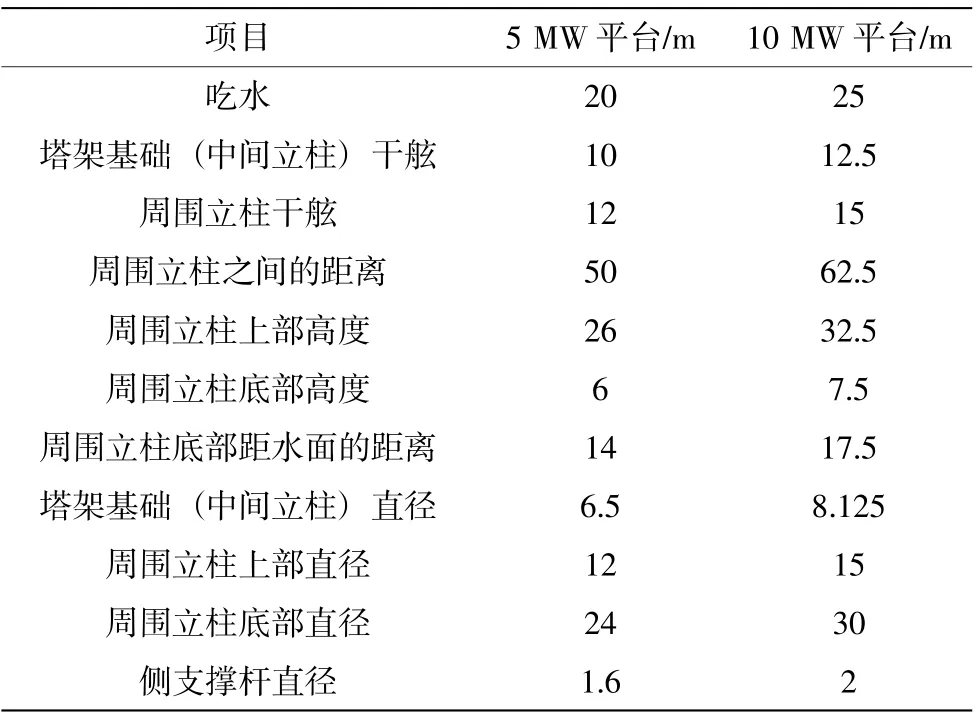
表2 半潜浮式平台模型参数

图4 OC4-DeepCwind 半潜浮式平台
2.2 数值验证
2.2.1 风机气动性能验证
根据网格收敛性验证结果,兼顾到计算效率,最终确定网格总体数量5×106。在叶片表面设定边界层为5 层、增长率为1.3,表面最小网格尺寸为0.008 m,网格如图3 所示。网格运动区域采用滑移网格技术,使用SST k-ω 湍流模型,在速度入口定义恒定的均匀风速。翼型网格划分如图5 所示,风场区域和边界划分如图6 所示。

图5 叶片截面网格

图6 风场区域划分示意图
选取了8 m/s、10 m/s、11 m/s、12 m/s、16 m/s、25 m/s 六组作业风况对风机的推力和功率进行数值验证。在数值模拟时来流风速和叶轮转速要保持匹配关系。表3 所示DTU 10 MW 风机在不同风速下对应的额定转速和仰角。

表3 来流速度和风机转速
图7 所示不同风况下DTU 10 MW 风机推力和功率与CFD 参考值[23]的对比结果。
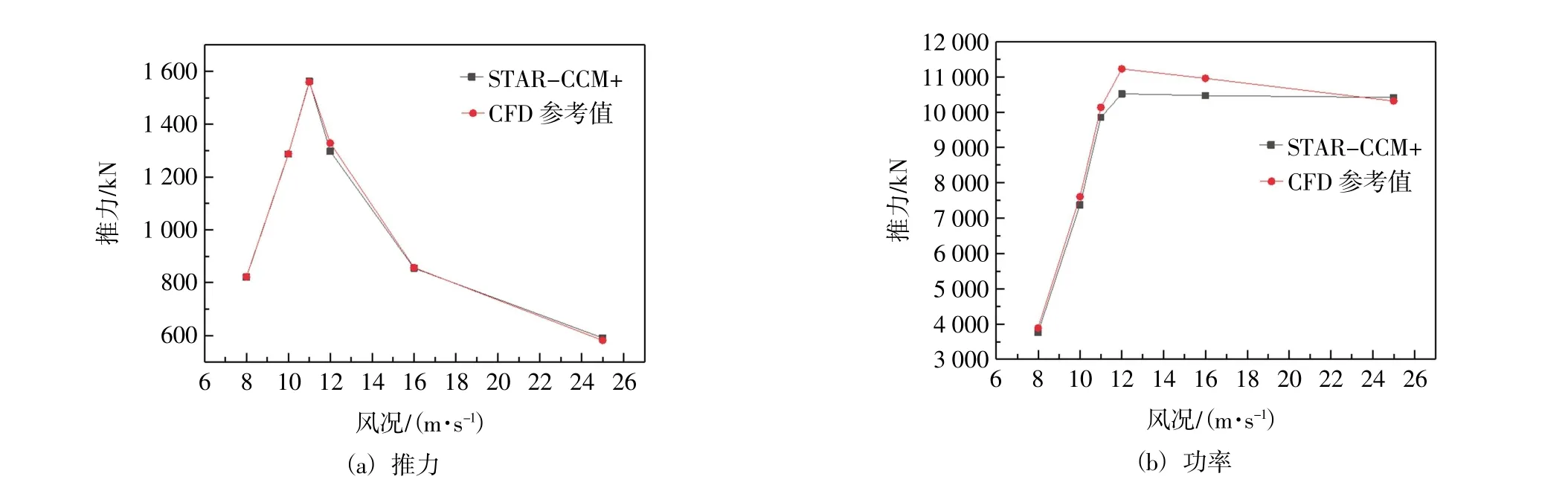
图7 不同工况下风机推力和功率
风机推力结果最大误差不超过3%,功率结果最大误差不超过7%,验证结果满足后续耦合计算要求,同时证明滑移网格技术对风机气动性能研究的可靠性。
2.2.2 自由衰减运动验证
图8 是半潜式平台的网格划分,包括自由液面区域、背景区域和重叠网格区域。考虑到计算效率和准确性的要求,网格总体数量2.8×106,表面最小网格尺寸为0.006 25 m,边界层5 层,增长率1.3[24]。图8 所示的是平台的网格划分结果。

图8 平台截面网格

表4 锚链布置及参数
系泊载荷是依据悬链线方程计算的准静态模型,其中包括由于悬链线质量和拉伸力引起的动态效应,这意味在整个计算过程中锚链和半潜浮式平台完全耦合的。在STAR-CCM+中的Catenary Coupling 模块中可以设置准静态悬链线耦合,在不考虑锚链躺底部分的条件下,悬链线耦合模块等效于浮式风机的系泊锚链的作用[22]。悬链线悬挂在两个端点之间,承受重力场导致的自身重量。在局部笛卡尔坐标系中,悬链线的形状由以下参数方程组给定。

参数值u1和u2表示悬链线端点在参数空间中的位置,表达式给定。


式中,g 为重力加速度;λ0和Leq分别是无力条件下悬链线的单位长度质量和松弛长度;D 为悬链线刚度;α 和β 为积分常数,取决于两个端点的位置和悬链线的总质量。锚链与平台连接示意图如图9 所示。

图9 平台系泊示意图
浮式风机系统的自由衰减能够获得自由运动的固有周期。本节兼顾计算效率的影响,只使用半潜浮式平台部分计算,但模型质量属性设置均与浮式风机系统相同。给平台一个初始的位移,然后释放,使其从初始位置自由移动。在静水条件下,使用SST k-ω 湍流模型分别对平台纵荡、垂荡、纵摇3 个自由度进行数值验证。图10 是半潜浮式平台自由衰减运动的时历曲线,结合下列方程计算出平台固有周期。

式中,t1时间点对应的运动幅值为A1;t2时间点对应的运动幅值为A2;t3时间点对应的运动幅值为A3。将图10 中的数值结果,带入上述方程便可以计算出对应周期T。
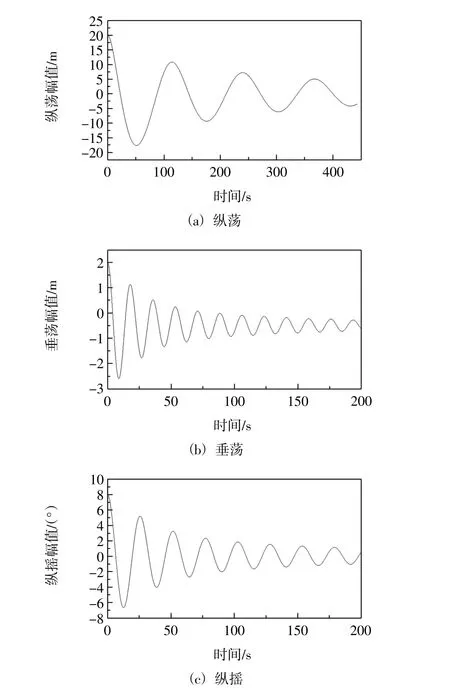
图10 半潜浮式平台运动衰减时历曲线
根据表5 中半潜浮式平台固有周期对比结果,可以看出纵荡的固有周期与试验结果[9]相差较大,这主要是由于准静态的悬链线模型在计算过程中是分段迭代求解,纵荡的位移远大于纵摇和垂荡,准静态模型在迭代求解的过程中会积累较大误差,但是纵荡误差没超过14%;垂荡和纵摇与试验值、FAST 计算结果[9]均小于5%,在误差允许的范围内。

表5 半潜浮式平台固有周期对比
3 半潜浮式风机耦合计算
本节着重考虑风浪联合作用下,浮式风机系统的运动响应。计算过程中并未考虑塔柱对流场的影响,但考虑到了整体系统的质量属性。选定额定计算工况,其风速为11 m/s,波高为3.66 m,波周期为9.7 s,风机叶片的额定转速为8.837 rpm。根据相似理论[25-26],采用1 ∶45 的缩尺模型进行计算。考虑到实际工程应用中,风力机有一个范围在0°至5°的预置仰角,所以本文通过改变风机叶轮俯仰角在0°和5°情况下,在风浪联合条件下对风机系统在水动力和气动力性能进行分析。
3.1 波浪验证
为了确保浮式系统能够准确地在波浪模拟中运动,本节所需的规则波工况是由计算域边界直接输入速度和压力完成的,STAR-CCM+的直接输入造波方法是基于波浪理论的精准方法,在开始数值计算之前对数值造波的准确性进行了验证。采用缩尺工况为周期1.45 s、波高0.081 3 m 的规则波,数值水池后端设有两倍波长消波区域。通过对比数值解和解析解(图11),计算发现其最大误差率仍低于5%,说明数值造波的准确度较高,可以用于后续的数值计算。

图11 波幅时历曲线
3.2 耦合模型网格划分
结合前面章节中网格划分的方案,整体计算域长14 m、宽9 m、高10 m,整个耦合系统中心距离速度入口5 m、速度出口9 m,距离顶部边界3 m、底部边界7 m。在风机叶片和浮式平台周围分别再创建网格加密区域来捕捉附近复杂的不稳定流动。整个网格区域共分成三大部分,即背景区域、风机叶片组成的滑移网格区域,以及浮式风机系统整体组成的重叠网格区域。风和波浪通过在速度入口施加速度和压力值实现。同时在水池前端施加波浪力,尾端施加阻尼消波,降低计算过程中背景波浪的影响。风机系统由DFBI 驱动重叠网格实现自由运动,风机叶片采用滑移网格技术套嵌在重叠内部,通过给定转速驱动叶片旋转。图12 所示耦合区域及边界划分,图13 所示耦合模型的计算流场。

图12 耦合区域及边界

图13 耦合计算的流场
3.3 风机气动力性能研究
本节预设风机叶轮仰角0°和5°两种结构,对风机的推力和扭矩进行了检测,根据扭矩数值结果进一步计算出风机功率,推力和功率结果如图14 所示。

图14 风机推力和功率时历曲线
根据图14,我们可以发现随着角度的增大,其推力和功率也相应下降,5°俯仰角的推力均值为9.45 N,功率均值为3.4 W;0°俯仰角推力均值为10.2 N,功率均值为4.4 W。5°俯仰角相较于0°俯仰角推力减小7.35%,功率减小25%。考虑到风载荷会对风机造成一个初始的纵摇角度,所以风机工作时的俯仰角都需要在设定角度的基础上,再加上纵摇均值角度。由于风机的受风面积随着叶轮俯仰角度的增大而减小,所以风机受到的推力减小,自然导致了整体功率的下降。
3.4 半潜浮式平台水动力性能研究
本文在数值模拟过程中,对浮式风机系统3 个自由度运动(纵荡、纵摇、垂荡)及系泊张力进行了检测。由于风载荷和波浪载荷带来的瞬态效应,使平台在计算前期产生了较大非线性运动,因此本文主要针对数值计算后期较为平稳阶段进行研究分析。
根据图15、图16 和图17 时历曲线可以看出随着角度增加,幅值和均值都减小了。主导因素是叶轮角度改变导致风载荷对叶盘作用面积减小。同时由于波浪载荷带来的瞬态效应,使平台在计算前期产生了较大周期性的振荡,因此下面主要对计算后期较为平稳阶段进行分析研究。相较于0°,俯仰角为5°时的纵荡幅值减少了5.26%,幅值均值减少了3.56%;纵摇幅值减少了1.22%,均值差别不大;但是垂荡方向上幅值变化不大,几乎一致。

图15 纵荡运动时历曲线
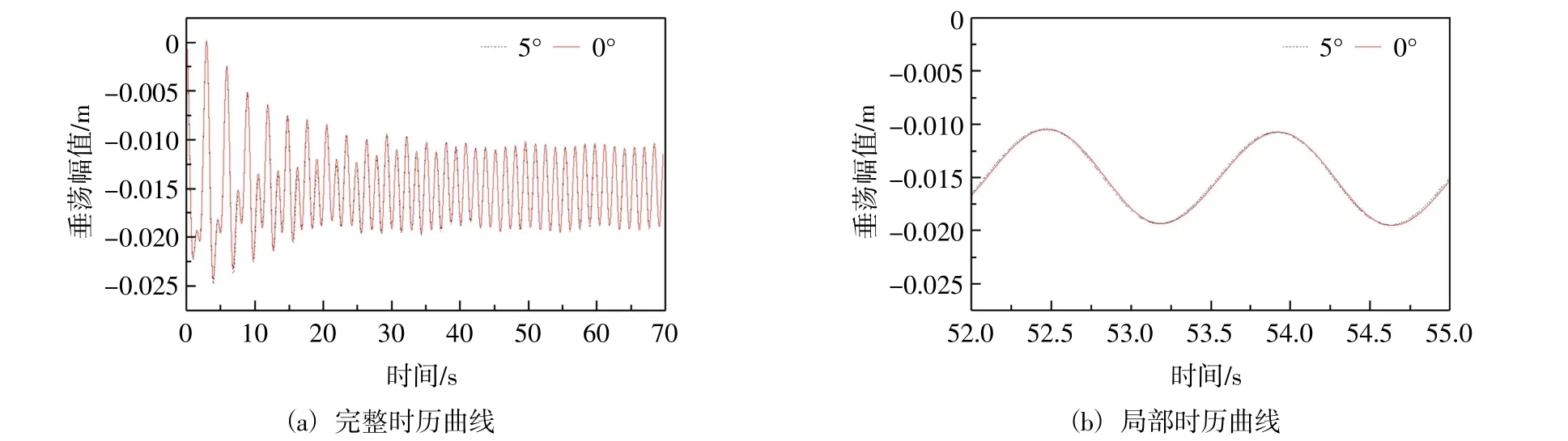
图16 垂荡运动时历曲线
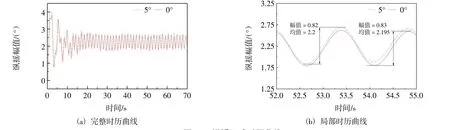
图17 纵摇运动时历曲线
根据图18 锚链1 张力时历曲线可以看出,5°俯仰角比0°俯仰角的锚链响应幅值和均值都减少了0.43%。根据图19 锚链2 张力时历曲线可以看出,5°俯仰角比0°俯仰角幅值减少了8.2%,均值增加了1.8%。锚链的运动响应和纵荡运动关联较大,仰角的增加势必会减小锚链的响应波动,因此适当增加俯仰角度有利于提高锚链寿命锚链幅值的波动容易影响锚链的整体使用寿命,故适当增大俯仰角可以提高锚链的寿命。

图18 锚链1 张力时历曲线

图19 锚链2 张力时历曲线
4 结 论
本文基于浮式风机耦合数值研究的现状,使用软件STAR-CCM+验证了DTU-10MW 发电风机的推力和功率,以及对DeepCwind 半潜式浮动平台进行了固有周期的验证。在此研究的基础上,通过对比不同叶轮俯仰角对半潜浮式风机系统的水动力和气动力性能进行分析,得到如下结论。
(1)基于SST k-ω 湍流模型、滑移网格技术、重叠网格技术及准静态悬链线系泊模块建立的数值模型,可以很好地满足半潜浮式风机系统的动态耦合模拟。
(2)根据动态耦合模拟结果,随着风机叶轮俯仰角度从0°到5°的改变,整个浮式风机系统在稳性上没有明显的变化;但在风机功率上,相较于推力的减小,风机功率减小比例更大。
(3)风机叶轮俯仰角度增加后,锚链1 和锚链2 的张力波动均减小,但锚链响应周期没有明显变化,所以在工程意义上适当调节俯仰角可以提高锚链的使用寿命。

