深圳海域垂直基准面的建立与统一转换

陈远鸿，杨志敏

(1.深圳市勘察研究院有限公司，广东 深圳 518000； 2.武汉市测绘研究院，湖北 武汉 430022)

1 引 言

获取地理空间信息的高程基准面依赖于大地水准面，国家和地区某区域的高程基准面通常由国家或者某区域多年来观测的验潮站资料确定的当地平均海平面，与实际的大地水准面有一定区别。由于不同地区采用的验潮站资料、方法和时间不一致，以及当地海水面变化、地形差异，各地区和国家的高程基准面存在较大差异[1]。因此，统一陆海高程基准与海洋深度基准对于国家经济发展、国防建设具有重要意义。目前国内外学者已对海洋测量垂直基准转换技术在工程化和实用化方面做了大量研究。在国外，学者们建立各种垂直基准参考面之间无缝拼接的转换模型，并研制了VDatum等工具软件及数据库，已经广泛应用于海岸带测绘产品的制作。近年来，国内学者在陆海高程基准统一方面也进行了大量的研究，为海岛(礁)测绘生产性试验提供技术支持[1～10]。

深圳地处我国华南地区，珠江口东岸，东临大亚湾和大鹏湾，西濒珠江口和伶仃洋，南隔深圳河与香港相连，是粤港澳大湾区四大中心城市之一。随着不断发展，深圳市不仅仅从陆地区域拓展范围，而且需要联合海洋一起共建国家级的海洋中心城市，则必须建立统一的海陆基准面。为实现深圳地区国家高程基准维护、海陆测绘基准统一，跨海大桥以及深水港口及其相关工程项目的实施，需建立高精度的深圳海域似大地水准面格网模型。本研究基于目前的国家空间坐标基准框架，广泛利用深圳海域已有的长、短期验潮站收集的潮汐基准面资料和区域内及周边的SZCORS等CORS站、高等级GNSS控制点以及水准点等提供的GNSS与水准数据，将这些资料与海洋重力及卫星测高数据综合起来，建立深圳海域高精度似大地水准面模型，在此基础上水文站的水准点将被纳入国家高程基准框架之内，从而统一深圳海域深度基准与国家陆地高程基准。此外，陆地高程基准被传递到深圳海域的海岛上，即实现陆海测绘基准统一。

2 海域高程基面和深度基准的转换模型建立

2.1 平均海面高模型建立

如图1所示为不同基准面之间的关系示意图。其中，似大地水准面与参考椭球面之间的联系通过似大地水准面模型给出，平均海平面与深度基准面之间的关系通过深度基准L值模型给出。为了建立似大地水准面和深度基准面之间的关系，需要建立深圳海域平均海面高模型，而平均海面高模型基于椭球面给出，进而建立两者之间的转换关系。平均海面高模型主要依据测高卫星数据和验潮数据计算得到，平均海面模型的构建主要通过三步进行[11，12]：

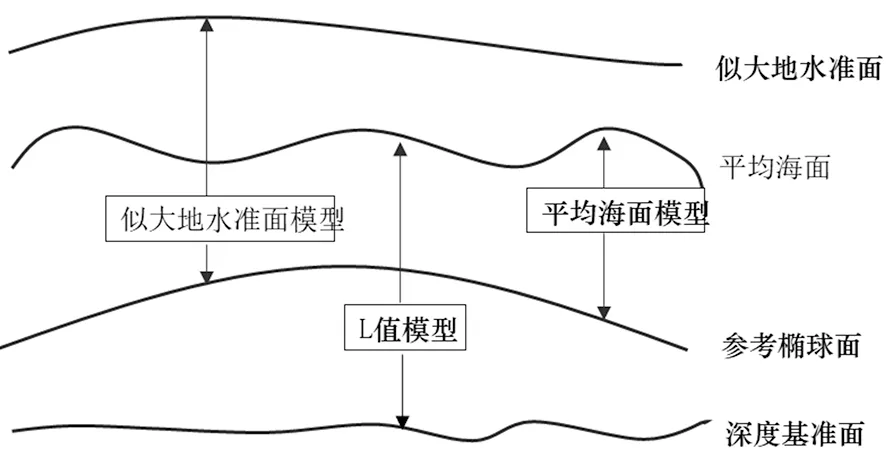
图1 海域高程基面和深度基准面的转换关系

(1)获取多源多代的卫星测高数据，并对数据进行预处理，删选有效观测数据以提高观测精度。

(2)对重复的轨道周期进行共线平差，削弱海面时变信号的影响。再联合共线平差后重复周期的数据和验潮数据来建立交叉点平差，以获得较高精度的离散平均海面高数据。

(3)对离散的平均海面高数据进行格网化，格网模型建立在Shepard方法、连续曲率张力样条方法和最小二乘配置三种格网化方法中进行比较择优，最终建立深圳海域平均海面高格网模型。

2.2 深度基准面L值模型构建

通过两步法可以构建深度基准面L值模型[13，14]：

(1)从精密潮汐模型获取每个网格点的调和常数，从深度基准面L值的定义算法出发计算生成L值格网模型；

(2)基于长、短期验潮站的L值订正第一步中得到的L值模型，使其在验潮站处的L值保持一致，同时将该模型的基准系统归化到验潮站使用的L值系统中，得到最终的成果模型。

潮汐模型是以动量方程、热传导方程等数值模拟区域的潮波传播，因海底地形、岸线、底摩擦系数等误差的影响，潮汐模型存在一定的误差。但对于每个潮波而言，数值模拟是以整个区域作为整体进行的，所以误差在空间上具有一定的规律性或至少与潮波的传播方向等相关，呈现区域的规律性。潮波同时具有前进波与旋转系统的特点，这种规律性不能简单地认定为系统性偏差。L值反映的是在理论上能够达到的最低潮位，其大小由主要分潮的振幅大小以及迟角组合决定。L值受到每个分潮的调和常数误差影响，但其传播是以复杂的非线性形式进行，据潮波系统的传播特点，有理由相信模拟误差在外海因分潮振幅相对较小，而对L值的影响也较小，所以本文只订正L值模型本身。因此，总体上对L值模型的订正方案是将略最低低潮面作为中介，把L值在验潮站处的差异传递到各网格点上。具体方法为：

(1)设立验潮站的有效订正范围为R，即每个验潮站只订正半径为R内的圆形范围内的网格点，或每个网格点只使用半径为R的圆形范围内的验潮站上的L值进行订正。

(2)对中短期验潮站与长期验潮站赋予不同的权重，两者之比确定为7∶10。

(3)统一以距离倒数定权。

某一网格点为例总结以上方案，设在其为中心R为半径圆周内的验潮站个数为n，验潮站L值差异为△Li，验潮站类型给予的权为pi(长期验潮站与短期验潮站分别为10与7)，与网格点的距离为Si，则该网格点的L值订正值△L为：

长期验潮站的数据在本文中起到对短期验潮站的L值传递以及订正、最终L值模型精度评估与订正等作用，因此，针对经常存在的长期验潮站数据不完备和缺失的问题，需要在数据处理之前对数据进行预处理和编辑，用以对缺失数据进行补充，本文采用的主要方案有以下两种：

(1)从附近的验潮站进行同期对比得到相关参数，然后对缺失的数据进行修复；

(2)根据长期验潮站其余的完好潮位进行潮汐分析得调和常数，然后再预报缺失的部分。

数据编辑完成后，本文将考证收集的长期验潮站现采用L值的算法，并按弗拉基米尔斯基算法定义重新计算L值，再检测验潮站相互之间的最低潮意义的一致性，具体技术工作如下：

(1)利用各站长期实测水位数据提取的主要分潮调和常数，按历史上曾采用的多种分潮组合算法计算L值，确定各站现采用L值的算法。

(2)按13分潮的理论最低潮面算法与最低天文潮面算法，计算各站的L值，评估现采用值的系统偏差以及空间分布情况。

(3)采用略最低低潮面与L值比值法、潮差比法对相邻长期验潮站间的L值最低潮意义的一致性进行检测。两种方法的原理如下：

①略最低低潮面(印度大潮低潮面)为4个最大主分潮M2、S2、K1与O1的振幅之和其基本原理是假设略最低低潮面值与深度基准面值成线性比例关系，数学模型为：

该方法为《GB 12327-1998海道测量规范》规定的深度基准面传递方法之一。

②由于理论最低潮面是理论上可能的最低潮面，故潮差越大，L值应越大，潮差法假设这种关系呈线性比例关系，数学模型为：

式中，RA、RB分别为两站的潮差。因此，该方法需要两站同步水位资料通过统计比较高低潮位来确定潮差比。

在深度基准面模型构建过程中，短期验潮站在沿岸对长期验潮站起关键的加密作用，将参与L值模型的精度评估与订正的作用。本文采用潮差比法与L值比值法，由邻近长期验潮站同步水位数据传递确定短期验潮站的深度基准面L值，并进行精度评定。

2.3 基于双线性插值法的目标点转换参数的确定

由于本文中各模型成果均由格网给出，因此需采用双线性插值法确定目标点转化参数。如图2所示，其中红色点为已知数据点，绿色点为待插点。假如我们想得到未知函数f在点P=(x，y)的值，若函数f在Q11=(x1，y1)，Q12=(x1，y2)，Q21=(x2，y1)，Q22=(x2，y2)，4个点的值已知，则先对x方向进行线性插值，可以得到：

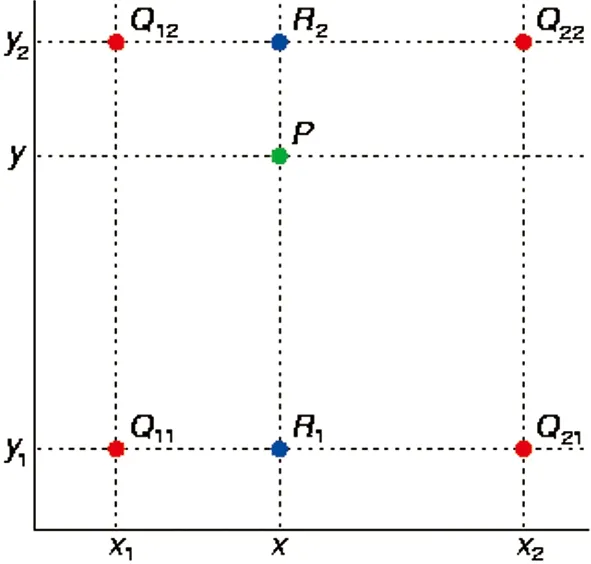
图2 双线性插值示意图

(1)

(2)

然后对y方向进行线性插值，可以得到：

(3)

最后即可得到所需结果：

(4)

3 数据计算结果

3.1 GNSS B级网数据处理结果

本文采用GAMIT V10.60软件进行基线处理[16]，这款软件是由美国麻省理工学院联合Scripps研究所共同研发的，采用了轨道精度达到 0.05 m的IGS精密星历，处理时加上在ITRF参考框架中测站坐标已知的全球站数据一起处理。由于精密星历提供的卫星坐标是瞬时记录，相应地面基准站坐标也应为瞬时坐标。网平差软件采用的是Power Adj科研分析版(PowerNet)，由武汉大学研制。对GNSS网进行处理时，首先采用GAMIT软件对同步观测网进行基线解算，然后平差时选取的观测量为各同步观测网的独立基线向量和其全协方差矩阵，程序采取“各独立基线构成最简基本回路”的原则自动完成独立基线的选取，兼容性好的SZCORS及2017年完成的深圳市GNSS B级网点的CGCS2000坐标为基准，对整网进行平差。在CGCS2000坐标系下得到的网平差结果表明，经过约束平差后，GNSS网的平均相对精度达到 0.051 0 ppm，最弱边相对精度为 1.147 6 ppm，其边长为 3 779.040 9 m(BINH-P003)；GNSS网中最弱点为P002，其水平精度为 0.008 0，大地高精度为 0.025 2 m。

3.2 一等水准数据处理结果

本文采用间接平差法对一等水准网实施平差，具体内容为：平差元素为加过正常水准面不平行改正、重力异常改正、标尺长度改正、海潮负荷改正、固体潮改正等改正后的往返测高差中数，未知数为待定结点高程，定权方式为按路线测站数赋予相应权值，按以上方法进行结点平差。当完成结点高程及路线高差平差改正量的计算后，对其他各水准点的高程采用附合路线平差的方法进行推算。一等水准网平差路线条数NC=17，已知点总个数NA=4，水准结点总个数NB=17，未知结点总个数N=13。1985国家高程基准下平差后每公里中误差为 ±0.35 mm，最弱结点高程中误差为 ±2.83 mm；1956年黄海高程系下平差后每公里中误差为 ±0.61 mm，最弱结点高程中误差±4.52 mm。

3.3 似大地水准面确定

本文在深圳陆海似大地水准面确定过程中，按以下方案进行计算：

点重力数据：2 185个，GNSS水准资料：98个；

参考重力场：ENGEN6C4地球重力场模型；

大地水准面的计算方法：第二类Helmert凝集法；

格网重力异常内插及推算估计方法：基于航天飞机雷达地形测绘使命(Shuttle Radar Topography Mission，SRTM)所获取的7.5″×7.5″高分辨率地形数据，在进行地形均衡归算后采用移去-还原原理进行计算。

地形均衡归算方法：基于Airy-Haiskanen均衡模型，使用了考虑地球曲率的严密球面积分公式进行均衡改正和地形改正，积分半径为 300 km。

离散重力异常内插为格网异常方法：曲率连续张量样条算法。这一方法能显著提高重力数据稀少、分布极度不均匀以及地形复杂地区的格网空间重力异常的内插及推估精度。

似大地水准面的计算方法[15]：第二类Helmert凝集法。这种方法可有效地测算大地水准面外部质量以及凝集层的地形引力和地形位的影响并加以改正，上述影响包括由凝集层位间的残差地形位和牛顿地形质量引力位带来的间接影响以及由地形质量引力位和凝集层位对Helmert重力异常所产生的引力影响，计算以上地形的直接和间接影响的过程中采用的积分半径均为 300 km。

按以上方案得到的结果如图3所示：

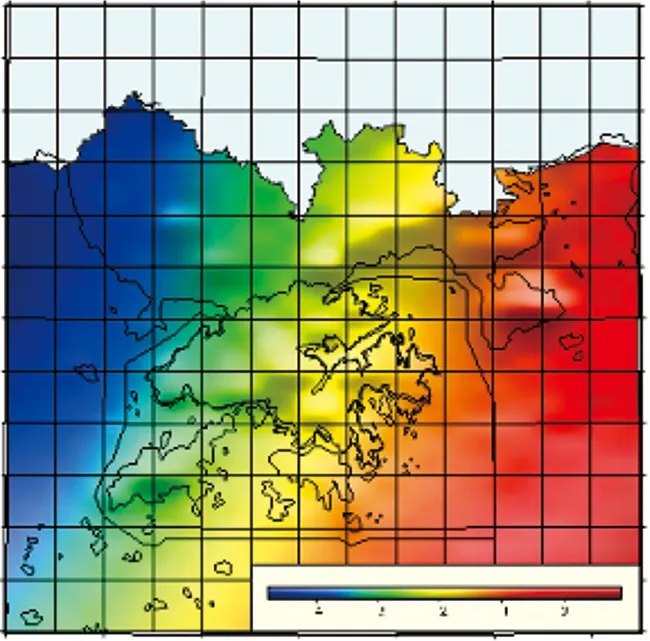
图3 2′×2′GNSS重力似大地水准面图(m)

将GNSS水准资料和重力似大地水准面进行独立比较，精度为 ±0.012 m。进一步地，基于球冠谐调和分析方法，将GNSS水准和重力似大地水准面进行联合求解，求得的2′×2′格网似大地水准面其精度达到 ±0.008 m。

3.4 海域似大地水准面与深度基准面转换

本文利用潮位站的观测数据和高程资料，在深圳海域建立深度基准面模型和高程基面向深度基准面转换模型。选取位于研究区域的3个站点进行对比验证，得到表1所示结果。本文选择13分潮的结果在3个站点对比验证，发现赤湾、惠州、盐田3个站点利用本文模型获取的13分潮订正的L值分别为1.378、0.960、0.947，与实测结果相比，两者间差分别为-0.039，0.007，0.002。实验结果表明，在某地点测得CGCS2000三维坐标，即可转换得到该点的海拔高和基于理论最低潮位面的高程。

表1 订正的L值与实测值偏差统计

4 总 结

为了进一步提高深圳市基础控制网的等级，实现深圳市优于3cm精度的海域似大地水准面模型，使深圳市现代测绘基准形成高精度、动态、三维以及几何基准和物理基准相统一的体系，本文在SZCORS的基础上，利用高精度GNSS静态相对定位和精密水准方法，建立深圳市陆海统一的高精度三维空间控制网和高程控制网。通过建立似大地水准面和深度基准面之间的关系以及深圳海域平均海面高模型，进而建立两者之间的转换关系。赤湾、惠州、盐田三个点的实测资料表明本文模型利用CGCS2000三维坐标，可以转换得到该点基于理论最低潮位面的高程。