不同锚具锚固效果及最佳限位距离研究
彭传阳,陈 强,方宗平,汪 波,陈 粟
(1.西南交通大学地球科学与环境工程学院,四川 成都 611756;2.四川交达预应力工程检测科技有限公司,四川 成都 610000;3.西南交通大学 交通隧道工程教育部重点实验室,四川 成都 610031)
0 引言
预应力锚索作为一种主动支护手段,能够有效提高岩土体稳定性和强度,改变岩土体内部自身应力状态,因此被广泛应用于边坡、基坑等工程中。然而,在我国地下工程中预应力锚索的发展却极不平衡。矿业领域较早地引入预应力锚索支护且应用十分成熟[1-3],而在铁路、公路以及引水隧道等领域发展及应用相对较晚。预应力锚索在矿业领域成功应用后,近年来,部分学者受到这种及时主动支护理念的启示,尝试将其应用于其他地下工程并取得一定成效,例如苍岭隧道[4]、兰渝铁路新城子隧道[5]、京张高铁八达岭长城站[6]等。
对于深埋软岩大变形的公路隧道而言,目前主要还是采用传统及时强支护的措施,然而随着建设需要和技术进步,这种及时强支护难以满足所有工程[7]。基于此,渭(源)武(都)高速公路木寨岭隧道采用预应力锚固支护,显著减少了围岩变形稳定时间与围岩变形潜势[8-9]。锚固效果是指岩土体在受到锚杆(索)作用后,内部应力得到改变,使得其整体性和强度提高,在这过程中锚杆(索)锚固体系所发挥的作用及其效果。在预应力锚固支护构件中,锚具处于十分重要的位置,它影响着预应力的传递和损失,而预应力值大小又影响着锚固效果。然而,国内外学者对锚具的研究较少,且基本从改变锚具结构尺寸参数、材料等方面研究锚具的力学性能、承载能力等。例如:Nanni等[10]针对夹片和锚索之间的摩擦及剪切力,对传统锚具提出改进措施;Al-Mayah等[11]通过试验研究预紧力和各接触面摩擦因数对夹片式锚具的影响,从而提出对传统夹片式锚具的改进;Shaheen[12]从改变锚具材料角度出发,在锚具的混凝土中加入碳纤维增强活性粉末,增强了锚具的抗裂性能;赵通等[13]通过有限元分析得出,锚具的锥角取值在6.5°~7.5°时,锚具的力学性能较好;刘建月等[14]通过有限元分析得出锚环锥角为6.5°~6.8°时能明显提高锚具的承载能力;许良昊等[15]通过有限元模型和室内试验获得了CFRP锚具最佳锚固性能的结构参数;周建林等[16]建立了多孔锚具参数化非线性有限元模型,得到锥角在6.0°~7.5°时,锚环应力变化不大;周明华[17]通过大量的调查和试验,得出锚具和钢绞线共同影响着锚具的锚固性能。
由于预应力锚索支护在我国公路隧道领域处于初步应用阶段,目前还没有针对公路隧道的专用预应力锚固构件,施工现场均采用矿用锚具,而常用的矿用锚具在锚环锥角、夹片锥角、锚具长度以及材料等方面存在差异,不同锚具会呈现出不同的锚固效果。当采用限位张拉时,不同锚具所搭配使用的最佳限位距离也有所差别,若限位距离和锚具匹配性较差,则会导致锚索预应力损失过大或锚具滑脱[18-19]。因此,在选择合适的锚具后,还应当确定与之匹配的最佳限位距离[20]。本文通过室内试验探究3种常见矿用锚具的锚固效果及对应的最佳限位距离,以木寨岭公路隧道为依托进行现场试验,验证室内试验得到的最佳限位距离。
1 锚具受力原理及结构分析
1.1 夹片锚具受力原理
通常矿用锚具采用三片式夹片锚具,将锚具简化进行受力分析,如图1所示。根据锚具结构可知,锚具受力符合楔块原理,即夹片越往内径小的锚环方向受力,两者之间的夹持力越大,锚具越紧。
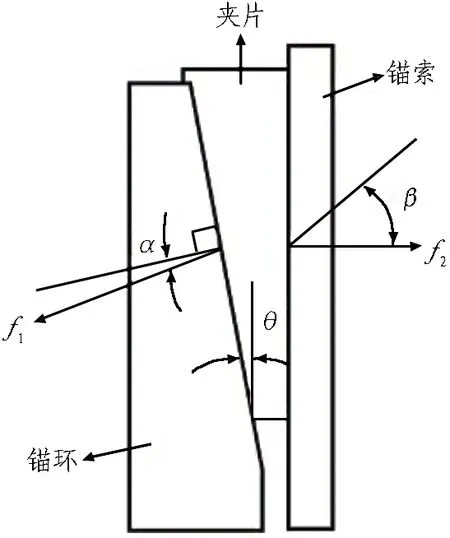
图1 锚具受力简化图
假设夹片与锚环的锥角均为θ,夹片与锚环之间的总压应力反力为f1、摩擦角为α,夹片与锚索之间夹持力为f2、摩擦角为β,则有:
f1h=f1cos(θ+α)。
(1)
f1v=f1sin(θ+α)。
(2)
式(1)—(2)中:f1h为f1水平分力;f1v为f1竖向分力。
对于夹片整体受力而言,水平方向应力大小相同,则有:
f1h=f2。
(3)
为了使夹片跟预应力锚索之间不产生相对滑动,那么必须满足f1v≤f2tanβ,即
θ+α≤β。
(4)
根据以上推导可知,锥角θ、夹片与锚环之间的摩擦角α两者之和应该在一定范围内小于夹片与锚索之间的摩擦角β。同时由于锚具尺寸不同,导致锥角θ不同,则锚具的受力情况也不同。那么,预应力锚索张拉过程中应力传递也会有所区别,即不同锚具在张拉过程中的锚固效果及预应力损失情况均不同。
1.2 不同类型锚具
从上述分析可知,锚具结构不同会导致锚具受力出现差异,因此,选取煤矿系统中常用的3种锚具(A型锚具,型号为MEF130621;B型锚具,型号为KM22;C型锚具,型号为KM22-1(1860))对3类锚具结构尺寸进行测量,具体尺寸见表1,结构示意见图2。

表1 3类锚具具体尺寸

(a)A型 (b)B型 (c)C型
对锚具尺寸进行测量,经过计算得到锚环和夹片的实际锥角如下:A型锚具锚环锥角为5.2°,夹片锥角为6.0°;B型锚具锚环锥角为6.0°,夹片锥角为5.9°;C型锚具锚环锥角为6.1°,夹片锥角为5.0°。可以看出,锚环和夹片之间的锥角差B型锚具最小,为0.1°;其次是A型锚具,锥角差为0.8°;C型锚具锥角差最大,为1.1°。
根据夹片锚具受力原理设定的锚环锥角与夹片锥角相等条件可知,当两锥角相等时,夹片与锚环完全贴合;而当两锥角不等时,夹片与锚环之间不能完全贴合,导致接触面变小,且随着两锥角差越大出现接触面积越小的情况。当接触面积和接触位置发生改变后,夹片受力也会随之发生变化,从而影响锚具回缩和预应力损失。可以看出,B型锚具夹片及锚环之间的锥角差最小、结构最佳。
2 室内试验
锚索在实际应用过程中的锚固效果及预应力损失受岩土体性质、地下水情况、张拉工艺、锚固段长度以及锚索与锚固剂的握裹力等因素影响,现场变量较多、机制复杂。因此,通过室内试验探究不同锚具的锚固效果及其最佳限位距离。室内试验在3 m锚索静载试验台座上进行,利用空心千斤顶进行锚索张拉。
2.1 张拉工艺
室内试验采用限位、分级张拉的方式对锚索施加荷载,限位张拉即在千斤顶和锚具之间安装带有限位距离的限位板进行张拉。此次室内试验设计限位距离为5、7.5、9、10、13、15、18 mm的对照试验,不同限位距离限位板见图3。分级张拉则是在荷载施加过程中以50 kN为梯度,依次逐级张拉至设计张拉控制值200 kN,每一级张拉完成后持荷30 s再张拉至下一级荷载,最后张拉至200 kN并持荷60 s后,千斤顶再缓慢匀速进行卸荷回油,整个卸荷过程的时间约30 s。各级荷载设计值及持荷时间为50 kN-持荷30 s、100 kN-持荷30 s、150 kN-持荷30 s、200 kN-持荷60 s。

图3 不同限位距离限位板
2.2 试验步骤
1)设备及仪器的安装。以A型锚具、5 mm限位板为例,张拉端各部件连接依次为空心千斤顶—5 mm限位板—A型锚具—垫板—振弦式压力传感器—垫板。各仪器具体连接见图4。

图4 锚索张拉端结构连接图
2)量测张拉前夹片外露距离。安装完毕后,在锚索张拉前,利用游标卡尺对夹片外露长度进行量测,读取3次量测数据,取平均值。
3)分级持荷张拉。按照前述的分级持荷张拉方式对锚索进行张拉,同时记录PT-20S锚下预应力检测系统显示的张拉力值与振弦式压力传感器显示力值。
4)量测张拉后夹片外露距离。张拉完成后,再次利用游标卡尺对夹片外露长度进行量测,读取3次量测数据,取平均值。
5)该组试验完成后,更换全新A型锚具和另一限位距离的限位板。
试验组命名及顺序:A型锚具搭配5.0 mm限位板为A1,7.5 mm限位板为A2,9.0 mm的限位板为A3,10.0 mm限位板为A4,13.0 mm限位板为A5,15.0 mm限位板为A6,18.0 mm限位板为A7。B、C型锚具命名同A型锚具,试验顺序以A、B、C及试验组序号大小的方式依次进行。
2.3 预应力损失计算
采用四川交达公司研发的PT-20S锚下预应力检测系统(简称PT-20S系统)对锚索进行张拉,张拉设备见图5(a);张拉控制力读数通过PT-20S系统显示,锚具后有效预应力值通过振弦式压力传感器显示,见图5(b)。记录锁定前PT-20S系统显示的最大张拉控制力为F1、振弦式压力传感器显示的锚下有效预应力为F2,计算得到预应力损失率k=(F1-F2)/F1。

(a)PT-20S系统
3 室内试验数据分析
3.1 不同锚具分析
通过室内试验探究A、B、C 3类锚具分别在限位距离为5.0、7.5、9.0、10.0、13.0、15.0、18.0 mm下的预应力损失情况。图6示出3类锚具在设计最大张拉控制力200 kN的情况下,预应力损失率与限位距离的关系。
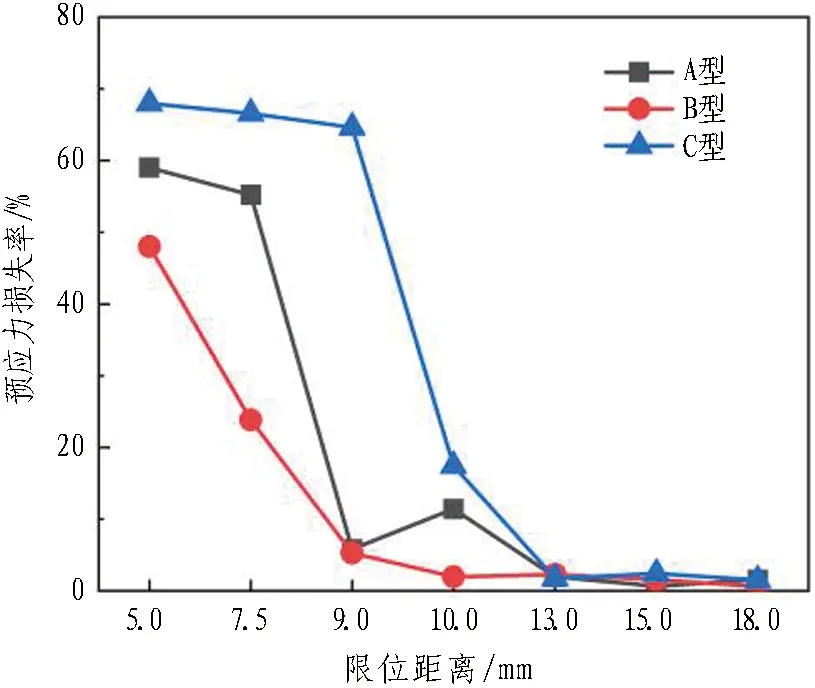
图6 不同锚具室内预应力损失情况
根据图6数据趋势可以看出,A、B、C 3类锚具的预应力损失均存在随限位距离增大而减小的趋势;并且在相同限位距离下,B型锚具的预应力损失率最小,当限位距离小于13 mm时更明显。此外,从预应力损失率与限位距离曲线可以看出,预应力损失率变化基本存在3个阶段:
1)慢速下降阶段。当限位距离低于某值,记为拐点x1,预应力损失随着限位距离的增大而缓慢下降。可以看出,A型锚具在限位距离为7.5 mm、C型锚具在限位距离为9.0 mm时均呈现出这样的趋势,因此可知B型锚具的拐点x1对应的限位距离应该小于5 mm。
2)快速下降阶段。当限位距离大于拐点x1后,预应力损失随着限位距离的增加而急剧下降。
3)稳定损失阶段。当限位距离大于某值,记为拐点x2,预应力损失率基本稳定,无明显变化。A、C型锚具的拐点x2均在13.0 mm附近,B型锚具的拐点x2在10.0 mm附近。
通过上述3个阶段可以看出,当限位距离大于拐点x2后预应力损失基本稳定,因此,可认为拐点x2即为锚具的理论最佳限位距离。
3.2 不同限位距离分析
3.2.1 锚具回缩长度
通过测量锚索张拉前后对夹片外露距离,得到A、B、C 3类锚具在不同限位距离下的回缩长度,具体数据见表2—4。
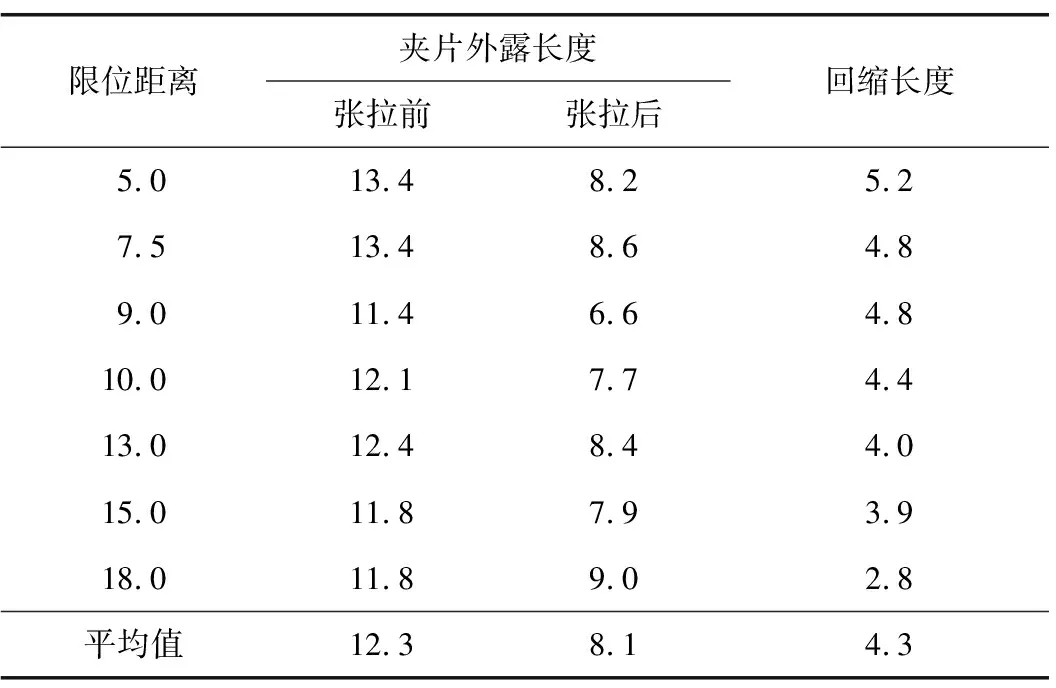
表2 A型锚具回缩长度

表3 B型锚具回缩长度
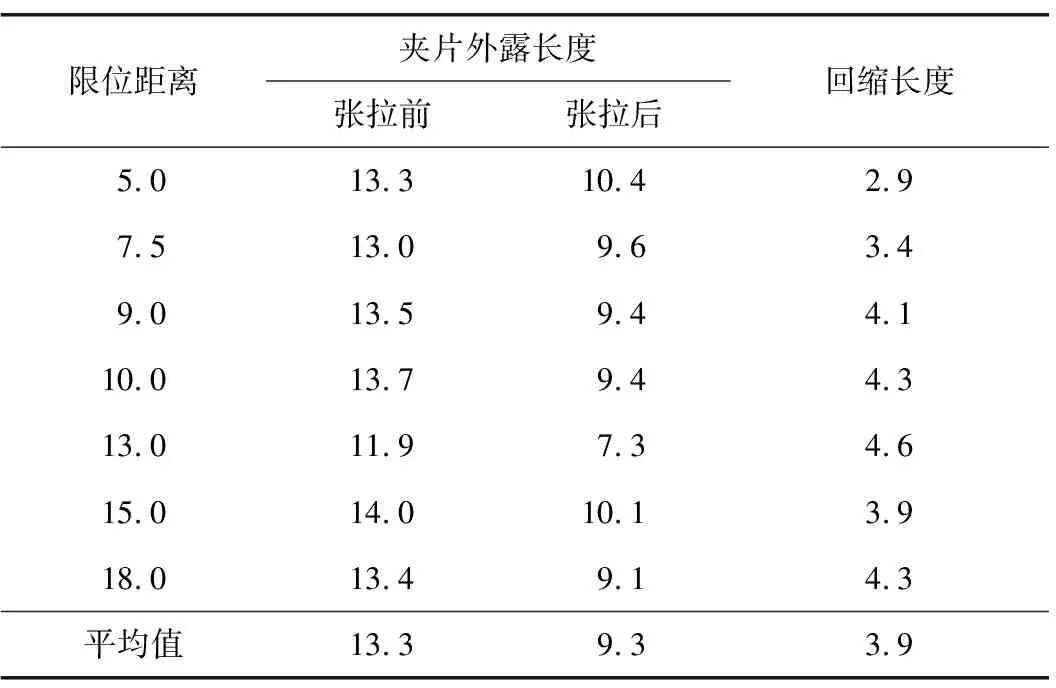
表4 C型锚具回缩长度
由表2—4可知,A型锚具张拉前夹片平均外露长度为12.3 mm,B型锚具张拉前夹片平均外露长度为10 mm,C型锚具张拉前夹片平均外露长度为13.3 mm,锚具张拉前夹片平均外露长度跟前述理论最佳限位距离相近。同时,锚具回缩长度随限位距离的增加有降低的趋势,总体呈负相关,表明在相同的张拉力值下,当限位距离较小时,夹片进入锚环的深度较大,说明在张拉过程中夹片向着锚环内侧发生相对滑移。从锚具平均回缩长度可以看出,B型锚具的平均回缩长度低于A型和C型,即再张拉过程中B型锚具夹片和锚环之间的相对位移小于A型和C型。
3.2.2 锚具刮伤情况
每次张拉结束后检查锚具夹片和锚索的情况。图7示出A型锚具在5.0、9.0、13.0 mm的限位距离下,张拉后夹片及锚索刮伤情况。
由图7可以看出,A型锚具夹片和锚索的刮伤程度随着限位距离的增加而减轻。当限位距离为5.0 mm时,夹片和锚索均受到严重的划伤,钢绞线上的刮痕明显且光滑,无齿印,钢绞线间可见刮伤后残余的铁粉;当限位距离为9.0 mm时,夹片和锚索也出现了较为严重的刮伤,但是其严重程度小于5.0 mm,锚索上可见夹片咬紧后的齿印;当限位距离为13.0 mm时,锚索上可见明显的齿印,未见刮丝且夹片基本没有变化。结合A型锚具回缩距离和预应力损失情况可以得知,当限位距离较小时,夹片对锚索的夹持力过大,而夹片向着锚环方向发生相对移动,夹片内部齿牙在移动过程中与锚索发生摩擦,使得锚索损伤,形成刮痕、出现刮丝,锚索预应力一部分用于克服两者之间的摩擦,导致损失过大。然而,随着限位距离的增加,限位板可直接和锚环接触,夹片和锚索之间的夹持力降低,两者之间的相对移动现象减缓,摩擦减小,于是锚索在张拉过程中的预应力损失降低。
通过上述现象和分析可知,限位距离越小,夹片和锚索的刮伤情况越严重,预应力损失越大。然而,限位距离并非越大越好,限位距离如果过大则会导致限位板和锚环之间存在一定孔隙,在张拉过程中限位板直接跟锚环接触,夹片未能被限位板抵住,锚环受力后容易发生锚具滑脱现象,同时限位距离过大也会导致锚索的回缩损失增加。从锚具的理论最佳限位距离可以得知,其预应力损失较小,且随着限位距离的增加预应力损失基本不发生明显改变。锚索张拉前夹片平均外露长度跟理论最佳限位距离相近,因此,为了便于快速施工,可通过测量张拉前锚具夹片外露长度确定实际最佳限位距离。根据上述分析,若限位距离大于夹片外露长度则有可能导致锚具滑脱,因此锚具的实际最佳限位距离应小于张拉前夹片外露长度和理论最佳限位距离。
综上所述,从锚具结构、相同限位距离预应力损失情况和锚具张拉前后的回缩长度综合分析可知,在相同的条件下,B型锚具的锚固效果优于A型和C型。此外,根据室内试验确定了3类锚具的实际最佳限位距离,其中A型锚具为12.0 mm,B型锚具为10.0 mm,C型锚具为13.0 mm。
4 限位距离现场试验及分析
通过室内试验可知,在A、B、C 3类锚具中B型锚具的锚固效果最佳,因此,将B型锚具用在木寨岭公路隧道进行现场试验,同时利用限位距离为9.0、10.0、11.0、13.0 mm的限位板进行限位张拉,验证室内试验中得到的B型锚具最佳限位距离10.0 mm。
4.1 现场试验方案
木寨岭隧道采用三台阶开挖法进行施工,一个开挖循环面布置19根锚索,其中,上台阶11根锚索,中台阶6根锚索,下台阶2根锚索。为了尽量避免岩体性质、地下水情况、锚索位置等变量的影响,将4组不同限位距离的限位板布置于间距为1.2 m的2个相邻循环面,其中9.0、11.0 mm位于1#循环面,10.0、13.0 mm位于2#循环面,每组循环面的限位板交叉布置,具体布置情况见图8。
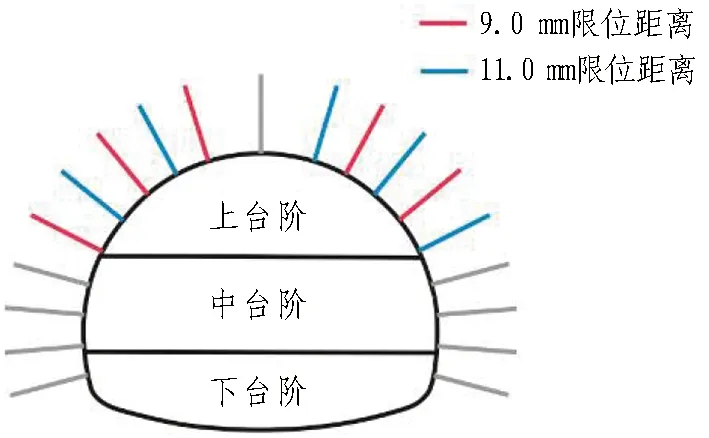
(a)1#循环面
通过现场调查可知,1#和2#循环面的岩体均为砂岩,节理裂隙均不发育,岩层产状、地下水情况基本一致,2个循环面的地质情况相同。现场试验情况见图9。锚索安装及施工情况如下。

图9 现场试验情况
1)结构组成。树脂锚固剂+21.80 mm锚索+W型钢带+300 mm×300 mm×15.50 mm垫板+矿用锚具。锚索结构见图10。

图10 锚索结构
2)锚索长度。锚索全长为5.0 m,其中自由段长3.5 m,锚固段长1.5 m。
3)设计张拉控制力为200 kN。
4)施工工序:钻孔—安装(搅拌)锚固剂—安装锚索、垫板、锚具—限位张拉—锁定。
4.2 试验结果分析
通过现场试验记录锚索锁定前最大张拉控制力及检测锁定后有效锚下预应力,采用室内试验相同的计算公式得到锚索预应力损失率,经过整理得到如图11所示的结果。

图11 不同限位距离现场损失情况
从图11可以看出,当限位距离大于等于10 mm时,平均预应力损失率出现了明显降低。10 mm限位距离的平均预应力损失率略高于11 mm和13 mm,是因为在限位距离为10 mm的锚索数据中有1根锚索出现了较大的损失,进而拉高了平均损失率。对比其他数据可发现,当限位距离大于等于10 mm后,预应力损失率基本保持稳定。然而,从现场试验得到的预应力损失数据可知,现场试验锚索预应力损失率明显高于室内试验,其原因受到多方面因素的影响:首先,由于现场试验环境相对室内试验而言更加复杂,锚索在张拉、锁定过程中受地质情况、孔道摩阻、施工操作等因素的影响,使得预应力损失增加;其次,由于室内试验中为了研究限位距离对预应力的影响而控制单一变量,没有考虑锚固段的影响,现场试验中虽然设计锚固段的长度均相同,在理论上对预应力损失的影响是相同的,但是锚索的实际锚固段长度却有所不同,并且在不同环境下锚索和树脂锚固剂的握裹力不同,因此现场试验中预应力损失率高可能跟实际锚固段的作用有关。从室内试验和现场试验得到的结果均可以看出,锚索预应力损失率与限位距离存在关系,当限位距离小于最佳限位距离时,预应力损失随限位距离的增加呈现出下降的趋势,当限位距离大于最佳限位距离时,预应力损失基本稳定。通过现场试验得到的结论可知,室内试验得到B型锚具最佳限位距离为10 mm的方法可行、结论准确。
5 结论与讨论
本文通过理论分析、室内试验的方法,探究了3类常用锚具的锚固效果及与之对应的最佳限位距离,以现场试验验证了确定最佳限位距离方法和结论的可行性和准确性,主要得到以下结论:
1)预应力损失率随限位距离的增加存在慢速下降、快速下降和稳定损失3个阶段,在快速下降和稳定损失阶段存在拐点x2,并认为该点即为锚具的理论最佳限位距离。
2)从锚具结构、相同限位距离预应力损失情况和锚具张拉前后的回缩长度综合分析可知,在相同的条件下,B型锚具的锚固效果优于A型和C型。
3)锚具的实际最佳限位距离应低于理论最佳限位距离和锚索张拉前夹片平均外露长度,则最佳限位距离A型锚具为12.0 mm,B型锚具为10.0 mm,C型锚具为13.0 mm。
4)通过现场试验验证了室内试验得到B型锚具最佳限位距离为10.0 mm的方法可行、结论准确。
5)需要指出的是,在本文研究中随着限位距离的增加预应力损失降低、锚具回缩距离减小的结论,跟实际生产应用中的结论趋势相反。本文所研究的小尺寸限位距离在工程应用中基本不考虑,属于特殊尺寸,此外,实际生产中基本不考虑夹片和锚索之间的摩擦而导致的预应力损失,随着限位距离的增加锚索的回缩损失也会增加,锚索预应力损失变大。
本文仅是研究现有常用的矿用锚具的实际锚固效果,选择相同条件下最佳的锚具应用于公路隧道中,然而实际公路隧道配套使用的锚固构件是否需要进行改进还有待进一步探索。同时,由于预应力锚索在公路隧道中处于初期应用阶段,因此许多研究尚未开展,理论明显落后于实践,包括本文中没有对锚固段进行研究,以及现场预应力损失较大的问题、锚固系统的力学机制等,都需要进行综合而系统的研究。
——钢绞线的断束断丝的防治及发生时采取的措施

