3-PUS-PU柔顺并联机构运动学分析与优化设计

周亚杰 李仕华 徐 奇 张凤奎

(1.燕山大学河北省并联机器人与机电系统实验室， 秦皇岛 066004; 2.燕山大学机械工程学院, 秦皇岛 066004)

0 引言

并联机构以其高精度、高刚度等优势，引起广泛的关注。其中，含恰约束支链的并联机构不仅能增大机构的承载能力，提升机构本身运动特性，而且不会影响原本机构的运动自由度，应用越来越广泛，大量学者对其进行了研究[1-6]。叶伟等[7]提出一种冗余驱动的三平移并联机构，对其进行运动学分析及优化设计。XU等[8]提出一种具有冗余驱动的2-RPR-P并联机构，对其驱动力进行分析。WANG等[9]提出一种具有恰约束分支的3-SPS-S并联机构，并对其运动学进行分析。LIANG等[10]基于3-RPS并联机构，采用五杆机构作为其恰约束运动链，设计得到一种具有恰约束支链的并联机构。

含恰约束支链的并联机构具有大的承载能力，但是传动精度过低的问题并未解决，而且由于加入了恰约束支链，增加了加工和装配难度。相比对应的刚性机构，柔顺机构作为一类利用材料的弹性变形来传递或转换运动、力或能量的机构，具有无间隙、无摩擦、免润滑、免装配等优点，能够实现高精度运动，大量的学者进行了相关研究[11-14]。

为得到性能优良的柔顺机构，XU等[15]提出以偏差路径和应变能为性能指标对柔性四杆机构进行参数优化设计，得到运动轨迹最优的机构构型。PAN等[16]以柔顺度指标对三平移柔顺并联机构进行优化设计。CHAU等[17]针对具有柔性杆与刚性杆的机构运动精度不高的问题，提出一种智能优化算法，实现二自由度柔顺并联机构输出运动的优化设计。DWARSHUIS等[18]针对拓扑优化中变形量不易确定的问题，提出了一种运动学分析方法，实现了平面柔顺并联机构的运动学优化设计。崔浩洋[19]设计一种具有两转一移(Two rotations and one translation, 2R1T)运动柔性并联机构并对其进行热力耦合优化分析。ZHAN等[20]基于映射约束法对平面三自由度柔性机构进行优化设计。ZHANG等[21]提出一种三自由恒力柔性机构，并以力的波动变化为优化目标进行多目标优化设计。而柔顺机构刚度不足一直是限制其进一步应用的重要因素。

为了得到高精度、高刚度的柔顺并联机构，对含恰约束支链的柔顺并联机构进行了相关研究。ZHANG等[22]基于3-SPS-RPR并联机构，采用刚体替换法设计得到一种新型三自由度柔性并联机构，并进行优化设计。崔学良等[23]推导了3-RPS-UPS冗余驱动并联机构各支链的运动协调性方程，确立了冗余驱动支链的动力学方程，由此建立其目标阻抗控制模型。CHEN等[24]提出了4-UPS-UPU柔性并联机构并对其建立了非线性弹性动力学模型，并对其动态响应、相图、动力学行为进行了分析。然而，含恰约束支链的柔顺并联机构的优化设计方面研究不足，对其运动学性能指标少有研究。

基于空间调姿机构高精度、高刚度的设计要求，通过引入恰约束支链的方式，提高机构刚度。本文提出一种具有恰约束支链的3-PUS-PU柔顺并联机构，并对其进行运动学和工作空间分析，考虑空间环境的特殊性和具体的工作要求，提出定位精度指标和紧凑性指标，并对该柔顺并联机构进行参数优化设计，以期为样机加工提供依据。

1 机构描述及运动学分析

1.1 机构描述

如图1所示，该柔顺并联机构由动平台、定平台、3条完全相同的PUS柔顺支链和一条PU柔顺支链及3个音圈电机驱动器组成。柔顺支链中P、U、S分别表示柔性移动副、柔性虎克铰和柔性球铰。3条PUS主动柔顺支链提供运动，而中间恰约束柔顺支链PU为机构提供约束，该机构能够实现两转一移运动，自由度为3。

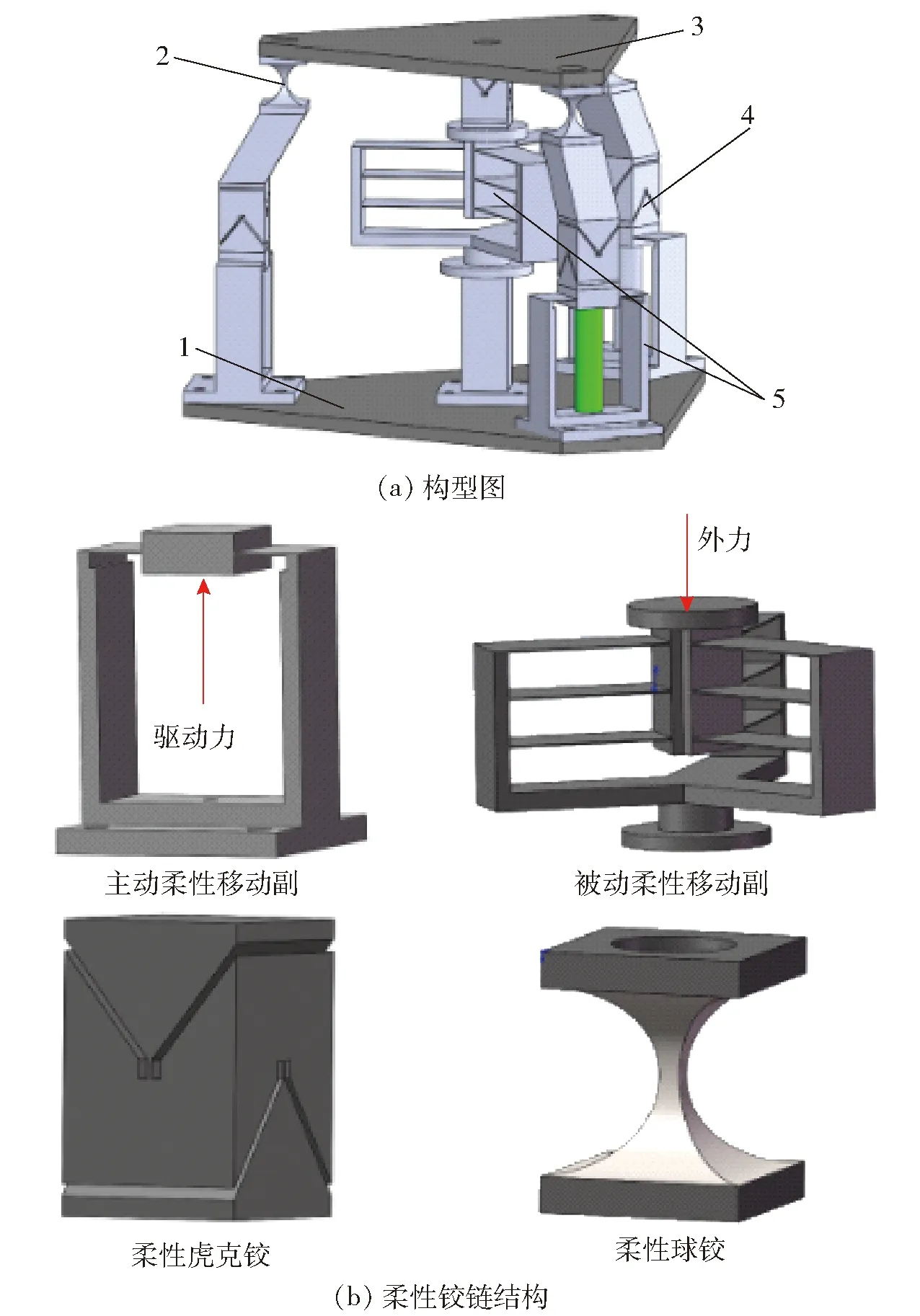
图1 3-PUS-PU柔顺并联机构Fig.1 3-PUS-PU compliant parallel mechanism1.定平台 2.柔性球铰 3.动平台 4.柔性虎克铰 5.柔性移动副

3-PUS-PU柔顺并联机构中的柔性铰链的具体结构如图1所示。PUS支链中的主动柔性P副采用平行四杆型柔性移动副，通过板簧的变形产生一个方向的位移。PU支链中的被动柔性P副采用簧片组合型柔性移动副，多个簧片组合增大了该柔性铰链刚度，进一步保证了机构高刚度的实现；通过施加外力引起板簧变形，对称设计保证了其具有更好的直线运动能力。柔性U副采用簧片形式的柔性虎克铰，由两转动轴线相互垂直的柔性转动副组成，来实现两个方向的转动。柔性S副采用双轴正圆缺口型柔性铰链，依靠柔性材料的变形来实现运动。

1.2 位置逆解

建立如图2所示的坐标系。Ai(i=1,2,3)表示PUS主动柔顺支链的P副与定平台相连的点；Bi(i=1,2,3)表示PUS主动柔顺支链的S副与动平台相连的点；Ci(i=1,2,3)表示PUS主动柔顺支链中柔性移动副与柔性虎克铰的交点；C4表示PU恰约束柔顺支链的移动副与柔性虎克铰的交点；B4在Bi(i=1,2,3)张成的平面B上，且位于平面B的中心位置，A0在Ai(i=1,2,3)张成的平面A上，且位于平面A的中心位置。以定平台中心A0为原点建立基坐标系A0X0Y0Z0，其中Z0轴垂直定平台向上，X0轴与A0A1重合，方向由A0指向A1，根据右手定则确定Y0轴。在动平台中心B4建立动坐标系B4X4Y4Z4，Z4轴垂直于动平台向上，初始状态下动坐标系B4X4Y4Z4与基坐标系A0X0Y0Z0各轴平行。

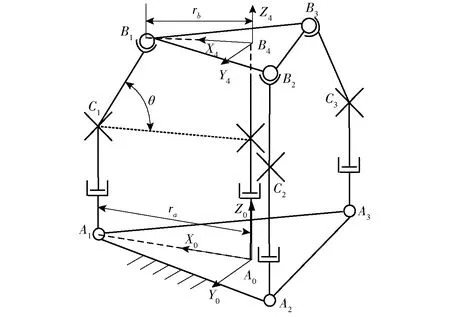
图2 3-PUS-PU柔顺并联机构结构简图Fig.2 Structural diagram of 3-PUS-PU compliant parallel mechanism

如图2所示，在基坐标系下，得到铰接点Ai和Bi(i=1,2,3)的位置矢量，建立闭环约束矢量方程，从而求出位置逆解。

定平台铰点Ai在基坐标系A0X0Y0Z0下的位置矢量为

(1)

在动坐标系B4X4Y4Z4下动平台铰点Bi的位置矢量为

(2)

在基坐标系中动坐标系原点B4位置矢量为

r=(x,y,z)T

(3)

在基坐标系下动平台铰点Bi位置矢量为

bi=R4bi0

(4)

其中

式中ra——定平台外接圆半径

rb——动平台外接圆半径

R4——旋转变换矩阵

α——绕X0轴旋转角

β——绕Y0轴旋转角

根据空间闭环矢量法，在基坐标系A0X0Y0Z0中，该柔顺并联机构闭环矢量约束方程为

(5)

式中qi——主动链中移动副长度

w——移动副单位矢量

q4——PU支链杆长

li——各支链中定长杆长

wi——各支链定长杆单位矢量

联立式(1)～(3)得到机构位置逆解表达式为

(6)

1.3 速度分析

根据3-PUS-PU柔顺并联机构的结构特点，将机构分解为3-PUS并联驱动子系统和PU串联约束子系统，分别得到并联部分的Jacobian矩阵和串联部分的Jacobian矩阵，进而建立整个机构的Jacobian矩阵，得到其速度之间的映射关系。

对于3-PUS并联驱动子系统，式(6)两边同时对时间求导可得

(7)

其中

ωX、ωY、ωZ——X、Y、Z方向的角速度

Ja——该机构并联部分的Jacobian矩阵

对于中间PU串联约束子系统，旋转矩阵R4的第3列恰为中间支链的单位向量。同时，动平台参考点B4坐标(x,y,z)也可以表示中间支链的单位向量，由对应关系可得并联机构的约束方程，整理得

(8)

动平台线速度和有效速度矢量之间关系为

(9)

式中Lp——中间变量

Jv——线速度对应的部分雅可比矩阵

动平台角速度和欧拉角α、β以及z之间关系为

(10)

式中Jω——角速度对应的部分雅可比矩阵

根据驱动方程和约束方程建立的运动学模型可以反映并联机构的整体运动特性，可以得到整个机构量纲统一的Jacobian矩阵

(11)

2 工作空间分析

采用数值法中的极限边界搜索法[25]进行工作空间的求解，首先确定机构杆长、运动副转角等约束条件，然后基于运动学位置逆解，采用极限边界搜索法得到机构的工作空间。

2.1 约束条件

3-PUS-PU柔顺并联机构的驱动器限制是限制其工作空间一个关键因素，根据工作空间的要求，本文选择直线音圈电机作为驱动器，确定其进给量

-5 mm≤qi≤5 mm

(12)

3-PUS-PU柔顺并联机构工作空间另一关键影响因素是转动副转动范围，故必须保证虎克铰和球较偏转角都在一定范围内。

对于柔顺并联机构，柔性铰链的极限转角同样是决定其工作空间的关键。如图3所示，本文采用双轴正圆缺口型柔性球铰和簧片形式的柔性虎克铰。

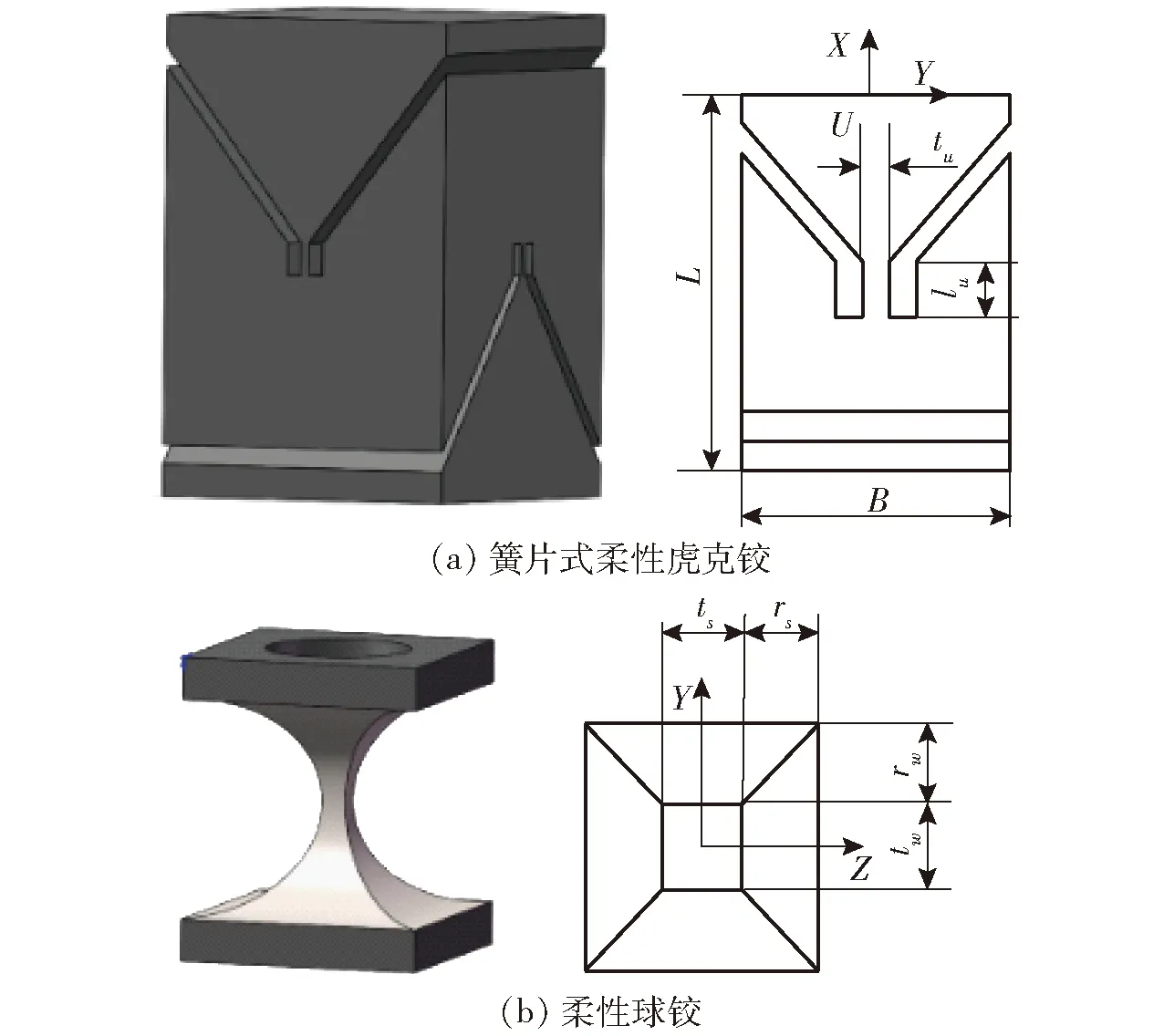
图3 柔性铰链示意图Fig.3 Schematics of flexible hinges

基于力学理论[26]求得柔性球铰和柔性虎克铰的极限转角为

(13)

(14)

式中Kφq——柔性球铰转动刚度

Kφh——柔性虎克铰转动刚度

WZ——抗弯截面系数

[σ]——许用弯曲应力

对于柔性球铰，影响其极限转角的尺寸参数主要为半径rs和中截面(最窄截面)的宽2ts，其极限转角与铰链结构尺寸参数关系如图4a所示；对于柔性虎克铰，其极限转角主要取决于簧片厚度tu和长度lu，其极限转角与铰链结构尺寸参数的关系如图4b所示。

图4 极限转角Fig.4 Maximum rotational angle

由图4a可看出，柔性球铰极限转角随着半径rs的增大而增大，初始变化比较平缓，当其大于某值时，转角呈指数式增大；极限转角随着最小截面ts的减小而增大，初始变化比较平缓，当其小于某值时，同样出现呈指数式增加的情况。由图4b可以看出，柔性虎克铰极限转角随着长度lu增加而增大，随着厚度tu减小而增大，且其厚度tu对其影响更加明显。

空间调姿机构的工作空间需要达到毫米级行程和角分级转角，首先需保证柔顺虎克铰的转动范围大于0.5°，柔性球铰转动范围大于0.2°，确定柔性铰链结构参数如表1所示。

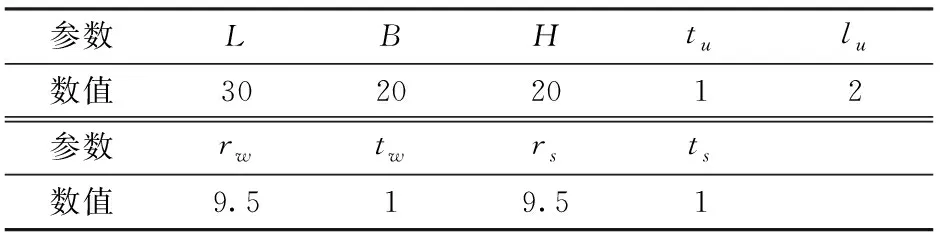
表1 柔性铰链结构尺寸参数Tab.1 Structure size parameters of flexure hinges mm

2.2 工作空间

3-PUS-PU柔顺并联机构的可达工作空间指其动平台上参考点所能达到的空间范围，选取rb=120 mm，ra=150 mm，θ=60°(定平台与PUS支链定杆的夹角，图2)，采用数值搜索法，得到3-PUS-PU柔顺并联机构的可达工作空间，如图5所示。

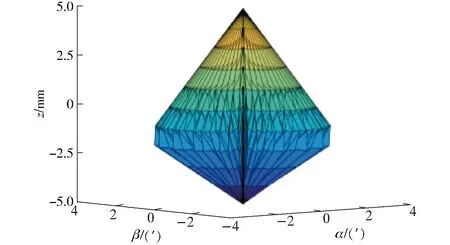
图5 3-PUS-PU柔顺并联机构的工作空间Fig.5 Workspace of 3-PUS-PU compliant parallel mechanism

由图5可以看出，3-PUS-PU柔顺并联机构的工作空间关于XOZ平面和YOZ平面对称，具有很好的对称性，整个工作空间内部没有空洞，连续性好。

其中绕X轴和Y轴的最大转动范围α=β=±2.5′，沿Z轴方向的位移最大行程z=±5 mm。由于其z向的位移由驱动副决定，所以不予考虑，用α和β两者之间的乘积表征工作空间VS，即

VS=αβ

(15)

3 性能指标分析

考虑空间调姿机构的工作需求及特殊的工作环境，提出定位精度指标和紧凑性指标，分析机构关键结构尺寸参数对其性能指标的影响。

3.1 定位精度指标

机构的Jacobian矩阵能够表征柔顺并联机构的运动学性能，误差放大因子能够表征柔顺机构的定位精度。即假设驱动单元输入速度有偏差δq，则动平台运动速度也会有偏差δp，可得

(16)

对式(16)两边取范数可得

(17)

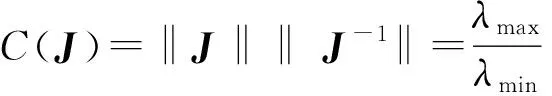
(18)

式中λmax——J的奇异值λi最大值

λmin——J的奇异值λi最小值

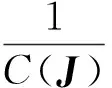
3.2 紧凑性指标

受使用条件的限制，对空间调姿机构大小提出了很高的要求，为表征工作空间与机构大小的关系，提出紧凑性指标。初始状态下动、定平台半径和高度乘积V表示其空间占用体积，空间调姿机构工作空间用VS表示，将VS与V的比值表征机构的相对占用空间，定义紧凑性指标EV为

(19)

为满足应用需求，需要保证机构具有紧凑的结构；为满足空间任务需求，需要保证调姿机构具有大的工作空间，在合理的结构尺寸范围内EV越小表示其紧凑性越好。

3.3 灵敏度分析

3-PUS-PU柔顺并联机构的主要结构参数为rb、ra和θ。采用保持变量法，分析机构的结构参数对定位精度和紧凑性的影响。

图6 的变化规律Fig.6

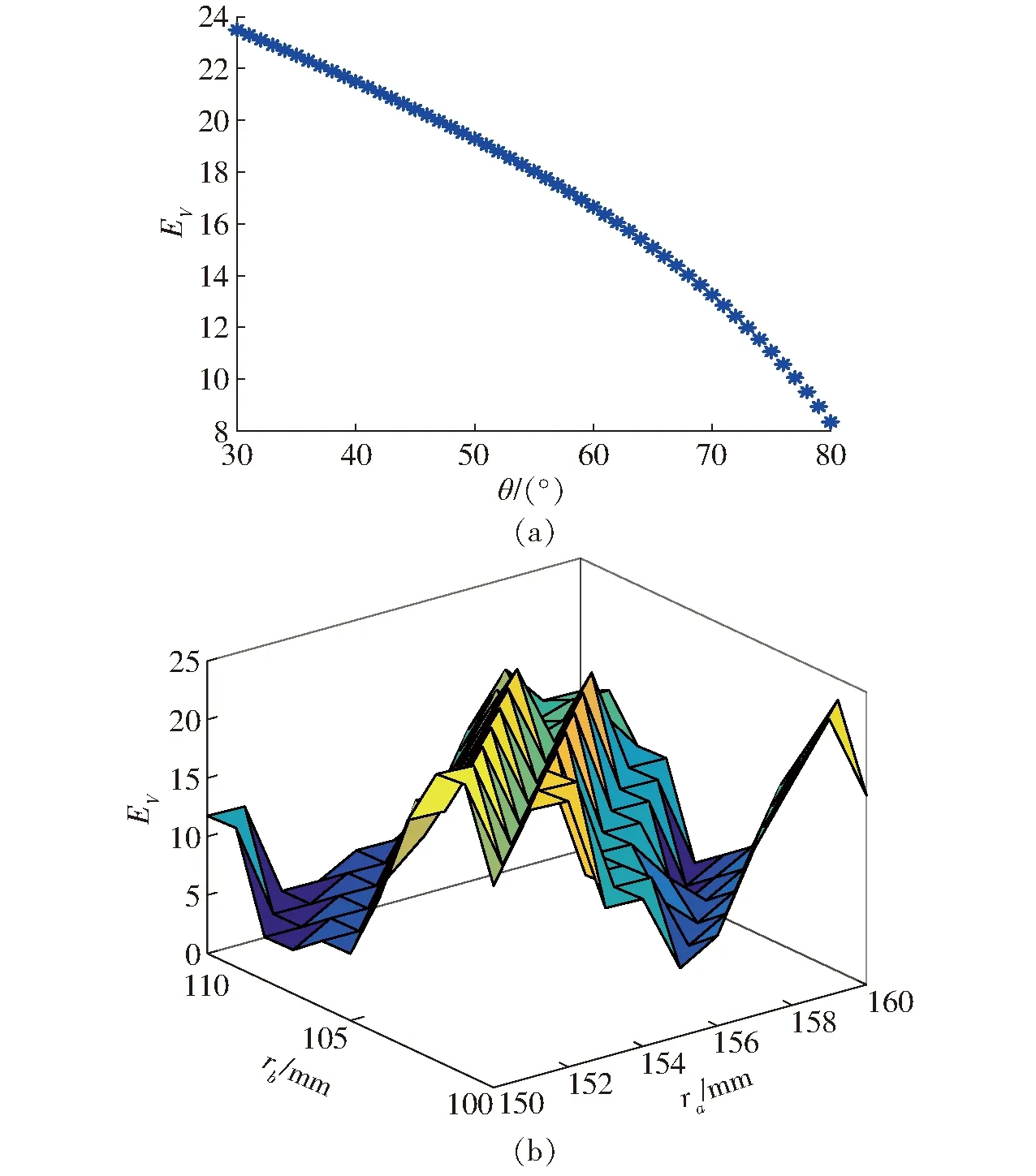
图7 EV的变化规律Fig.7 Change rules of EV

4 优化设计

4.1 数学模型建立

为得到一个确定的3-PUS-PU柔顺并联机构，需要确定3个设计变量，即ra、rb和θ(图2)。

对于3-PUS-PU柔顺并联机构，在工作空间足够且精度满足要求的前提下，通常希望机构结构越紧凑越好。根据第3节提出的定位精度指标和紧凑性指标，采用分配权重因子法将两个指标统一，得到机构的目标函数

(20)

其中

n1+n2=1

式中n1、n2——权重因子

C(Ji)——第i个位姿的雅可比矩阵条件数

EVi——第i个位姿的机构体积比

为保证3-PUS-PU柔顺并联机构设计方案的可行性，考虑实际的工况条件，给出3-PUS-PU柔顺并联机构的各设计变量的变化范围及初始值，如表2所示。

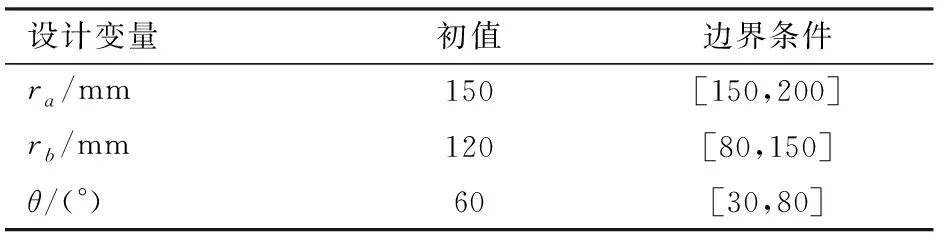
表2 机构主要设计变量Tab.2 Key design parameters of mechanism

4.2 优化算例

根据目标函数的比重，选取n1=0.8，n2=0.2代入式(20)，得到目标函数，采用粒子群算法(PSO)对3-PUS-PU柔顺并联机构进行结构参数优化计算，其中PSO的参数选择直接影响优化结果。本优化主要的PSO参数配置如表3所示，优化结果如表4所示，目标函数随迭代次数变化曲线如图8所示。

表3 粒子群算法参数Tab.3 Parameters of particle swarm optimization

表4 优化结果Tab.4 Optimal results

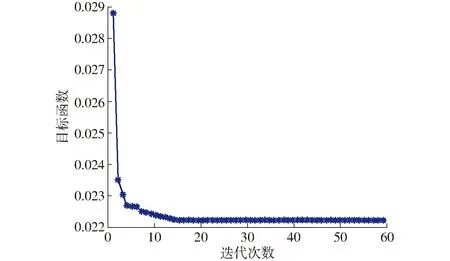
图8 目标函数变化曲线Fig.8 Curve of objective function values

由图8可以看出，随着迭代次数逐渐增大，目标函数逐渐趋于某一固定值，大约在第20次迭代，达到最优值，迭代速度较快。由此可以看出，建立的优化模型及选择的优化算法是正确、有效的。

由表4可以看出，优化后的3-PUS-PU柔顺并联机构的定平台外接圆半径ra、动平台外接圆半径rb和夹角θ都有所增大，其中ra和rb增大令机构的横向尺寸变大而θ的增大令机构的纵向尺寸有所减小，通过计算可以得到该机构的整体占用空间有所降低。

定位精度指标和紧凑性指标相比原方案有明显的增加，定位精度指标增加25%，紧凑性指标增加81%，最优目标函数提高25%。考虑到机构的实际加工精度和制造成本，将优化后设计的参数圆整，得到一组机构的优化设计参数为：ra=200 mm，rb=135 mm，θ=80°。并得到最优结果的机构的工作空间，如图9所示。

图9 机构优化后工作空间Fig.9 Workspace after optimization

图9表示优化后这组设计参数对应并联机构的工作空间，与未优化前相比，其工作空间由±2.5′增加到±2.56′。优化后机构的空间占用体积降低，工作空间增大，即紧凑性指标有所增大。由此可知，优化后并联机构的结构更加紧凑，具有良好的工作能力。该组优化设计参数可为后续3-PUS-PU柔顺并联机构的样机设计提供参考。

5 结论

(1)提出了一种新型高精度、高刚度的三自由度柔顺并联空间调姿机构。

(2)建立了机构的运动学模型，分析了机构的工作空间，进一步提出了定位精度和紧凑性指标。

(3)采用粒子群优化算法，对该机构进行了尺寸优化设计。结果表明，优化后的机构定位精度指标提高了25%，紧凑性指标提高了81%。