水体多环芳烃组分识别小样本分析方法研究

祝 玮，杨瑞芳，赵南京，殷高方，肖 雪，刘建国，刘文清

1. 中国科学技术大学环境科学与光电技术学院，安徽 合肥 230026 2. 中国科学院合肥物质科学研究院，安徽光学精密机械研究所，环境光学与技术重点实验室，安徽 合肥 230031

引 言

来自自然和人为来源的多环芳烃(PAHs)几乎存在于所有自然水环境中[1-2]。它们是有毒有害的有机污染物，对动物和人具有引发突变和致癌的威胁[3-4]。因此对实际水体中多环芳烃的快速现场监测十分重要。化学色谱法是一种理想的测量多环芳烃的方法，但是有比较耗费时间和耗费金钱的样品前处理，包括分析物的提纯和预先浓缩[5-6]。目前化学色谱法的替代方法是三维荧光光谱技术(TFST)[7-8]。TFST具有较高的灵敏度，是一种很有前途的快速、 无损地现场监测水生环境中荧光多环芳烃的技术[9-10]。它同时测量多环芳烃的激发和发射矩阵来获取各多环芳烃的荧光光谱信息，可作为区分不同种类多环芳烃[11]的特征指纹。然而由于部分多环芳烃的结构相近和自然水样的成分复杂，以致造成荧光峰重叠和未知荧光组分的干扰导致三维荧光光谱缺乏一定的选择性，阻碍了其直接识别水中多环芳烃污染的实用性。因此，成分光谱提取成为多环芳烃三维荧光光谱分析的主要研究热点之一，并发展了包括平行因子分析(PARAFAC)在内的多种多维分辨率方法[12-14]。

平行因子分析是当前应用最广泛的分析方法之一，它将三维荧光光谱数据组直接分解为相对浓度分数，激发光谱和发射光谱，从而获得底层荧光组分[15-17]。通过对多环芳烃[18]的激发和发射光谱与标准荧光光谱的比对，可以实现组分的定性识别。以上所引的研究工作都是试验混合物的数量大于或至少等于纯组分的数量的情况。但在实际应用中，样品数量过多是一项费时费力的工作。因此，从较少检测的样品中提取和识别更多的组分，即多组分三维荧光光谱的欠定分解，具有实际意义。在光谱分析领域对欠定分解的研究相对较少[19-20]。PARAFAC可以从较少的样品中回收更多的成分。但是，由于一些信号的荧光发射较弱，对于过少的样品，它可能会给出不准确的结果。奇异值分解(singular value decomposition, SVD)是一种有效的去噪工具，可以实现信号与噪声之间的无偏微分[21-22]。奇异值分解去噪的基本原理是保留奇异值显著的奇异分量。受此启发，利用SVD对微弱荧光信号的高亮进行了研究。

这里提出了一种基于奇异值分解(SVD)和PARAFAC的欠定分解方法。该方法通过选取有效奇异值重构观测样品的激发发射矩阵结构，解决了微弱荧光信号的突出问题。根据奇异值的特点，确定激励发射矩阵的最优结构作为信号的新的伪样本。将观测样品与新样品结合，利用PARAFAC得到纯组分光谱。最后，通过回收光谱与标准光谱的比较，识别出污染物成分。以多环芳烃为例，从两种多环芳烃混合物的观测光谱中成功地恢复了6种纯组分荧光光谱，并利用相似系数进一步评价其组分识别的效率。

1 方法原理

1.1 三维PARAFAC方法

作为一种三线性算法，三维PARAFAC可以对三维阵列进行如下分解(Bro 1997; Nikolajsen等2003年)[15，23]

i=1，…，I；j=1，…，J；k=1，…，K

(1)

式(1)中，x(i,j,k)是i样品的一系列尺寸为J×K(发射波长j，激发波长k)的激发-发射矩阵“叠加”而产生的三维矩阵x(I×J×K)的元素。其中I为样本数，J为发射波长，K为激发波长，F为因子数，每个F对应一个平行因子分量。aif为第i个样品中f组分的相对浓度，bjf和ckf分别为f组分在λj波长处的发射和检测波长λk处的波长激发。将aif，bjf和ckf的所有元素收集到三个加载矩阵A，B和C中，分别对应浓度分数矩阵，就可以计算出相应的发射光谱和激发光谱。

1.2 奇异值分解

开始的SVD过程将数据矩阵G分解为三个矩阵UM×N,SN×N和VN×N

G=USVT

(2)

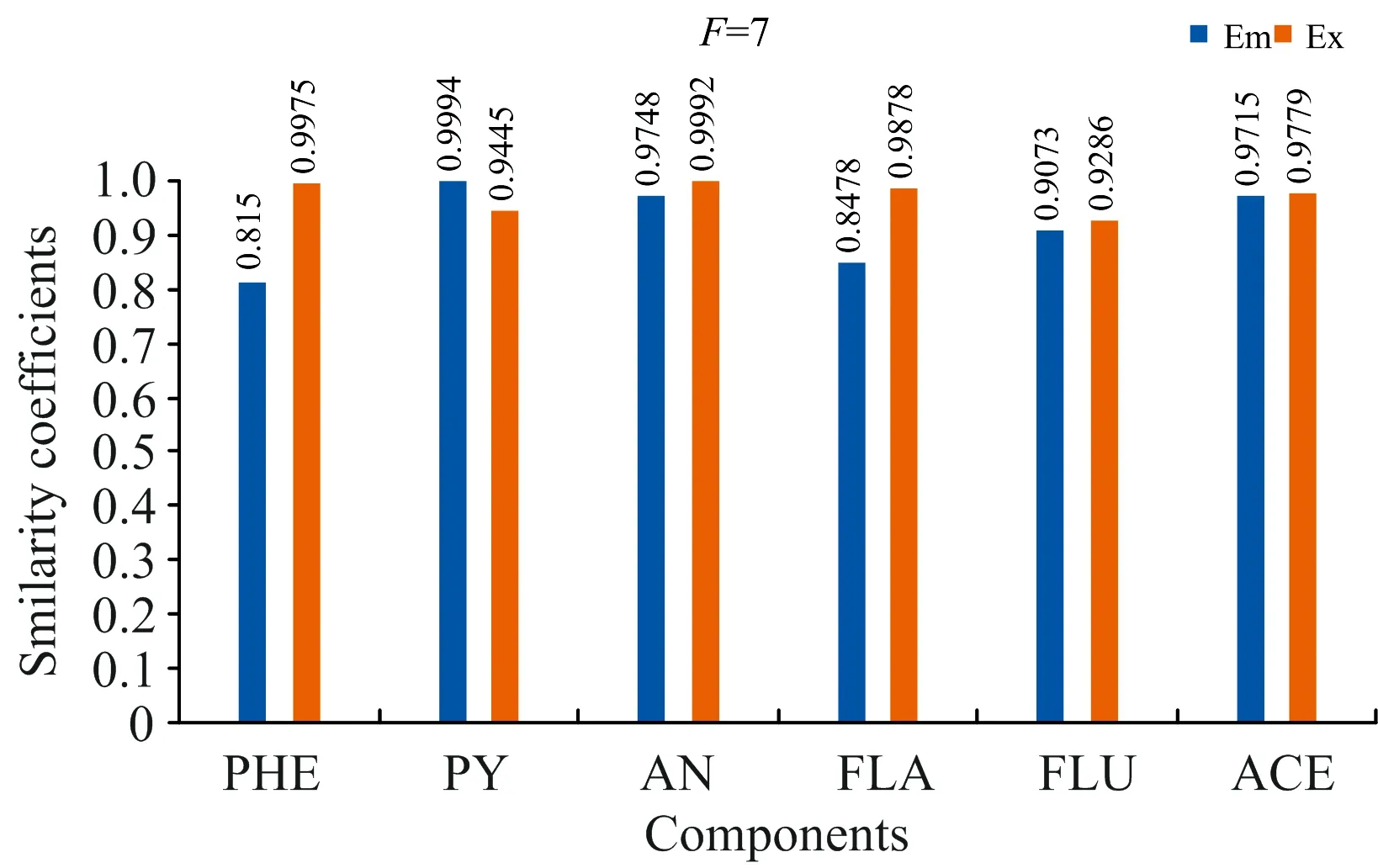
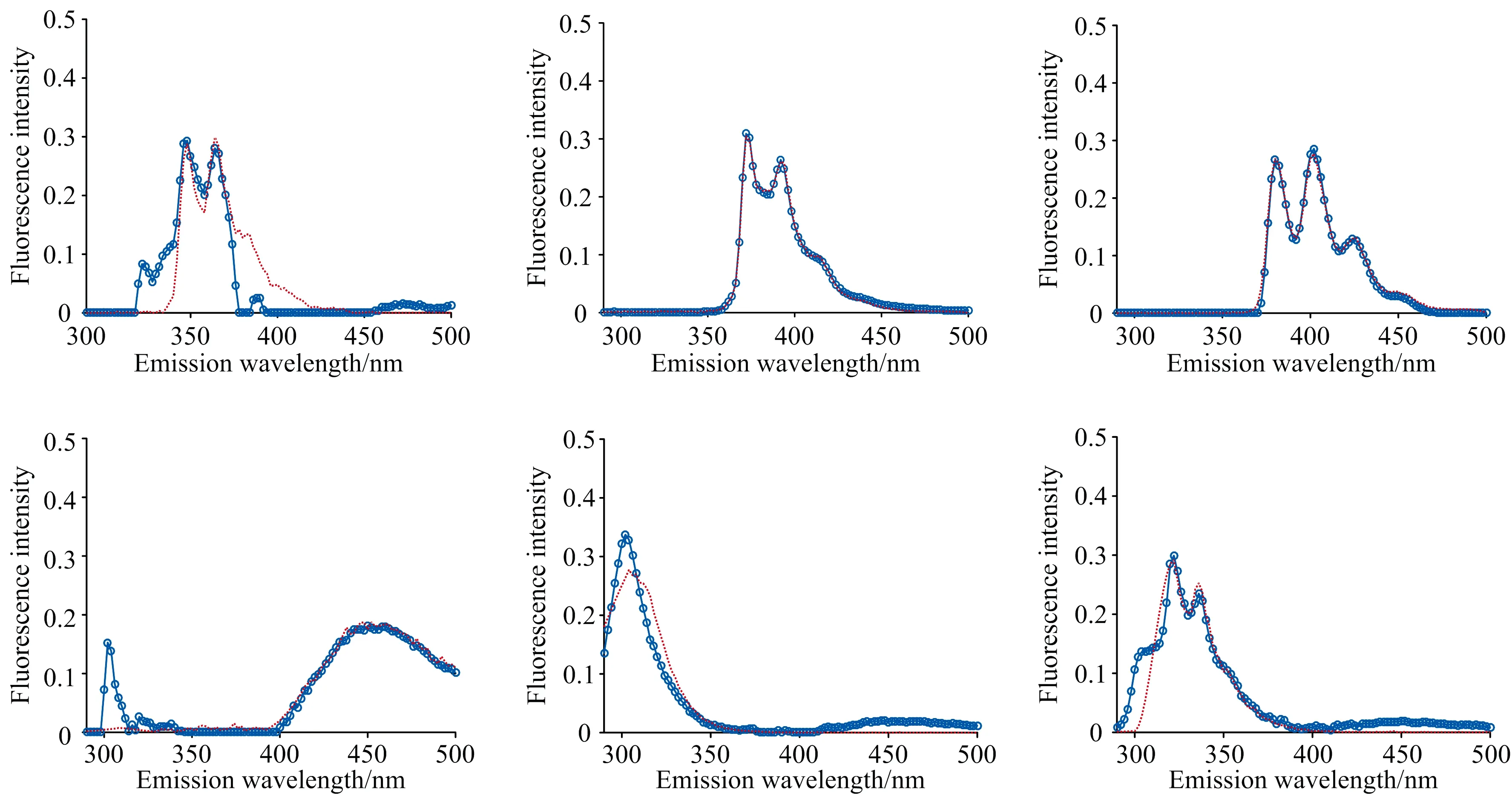
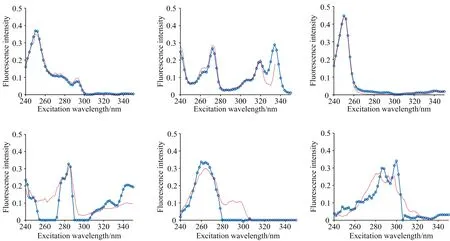
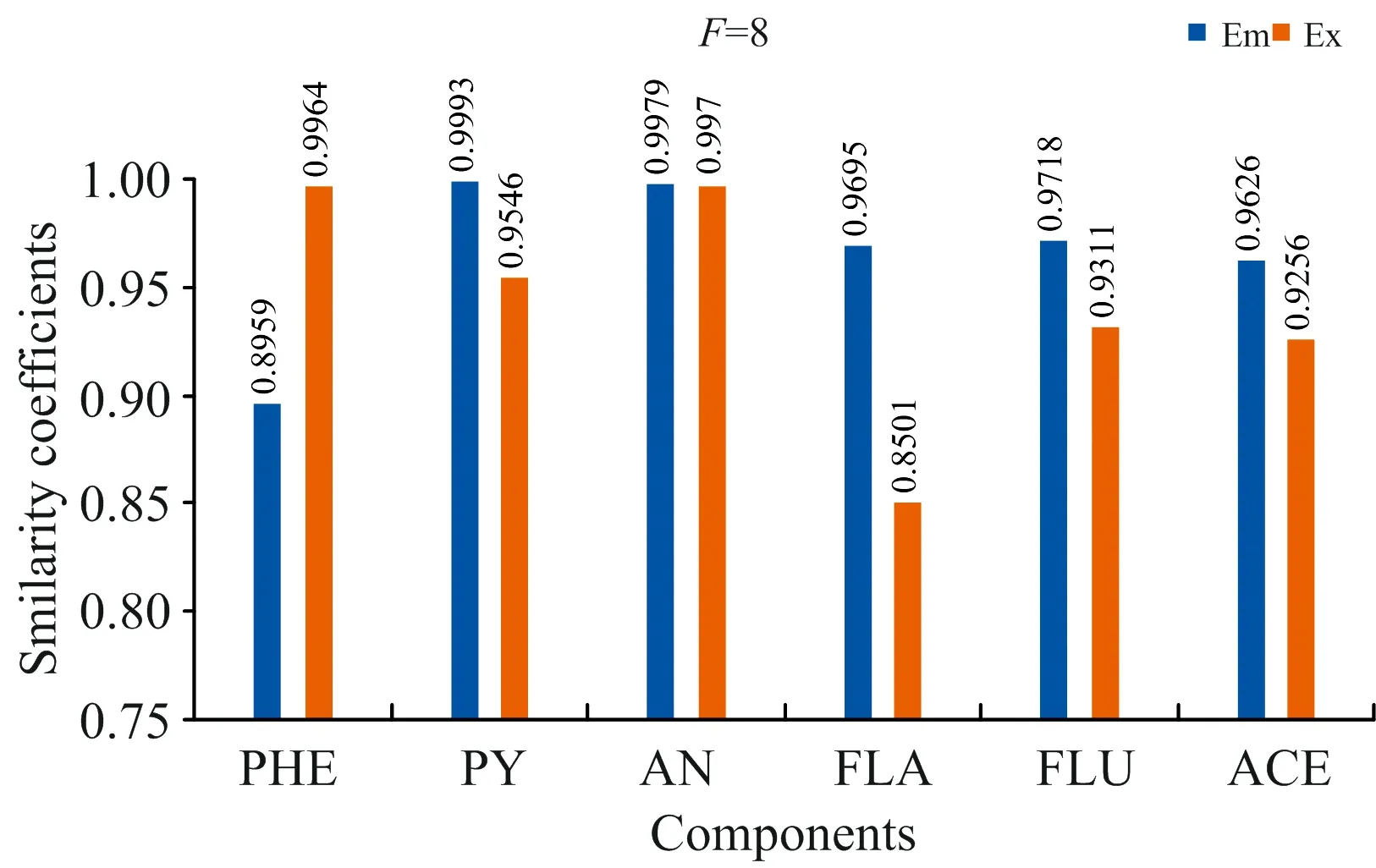
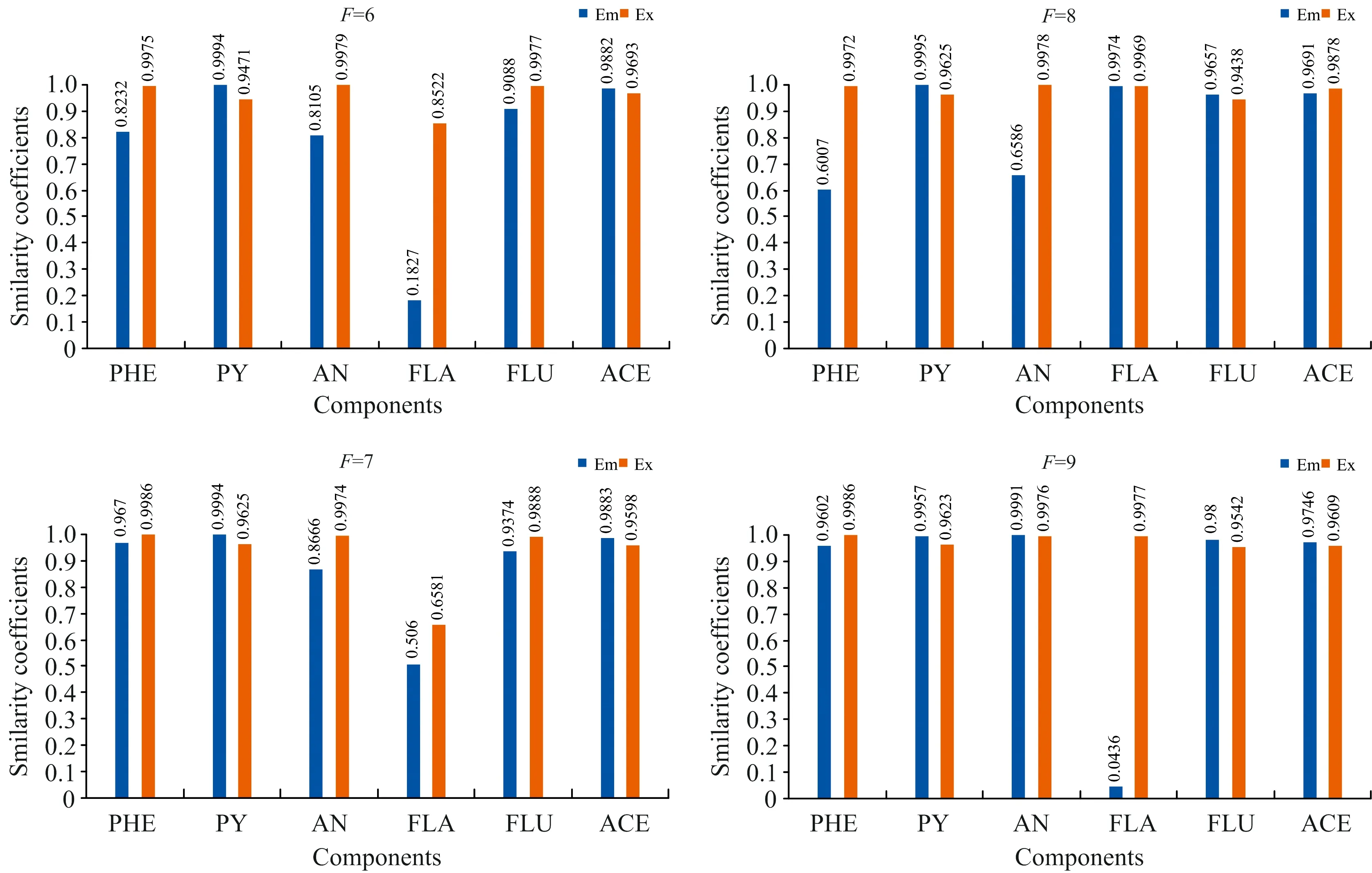
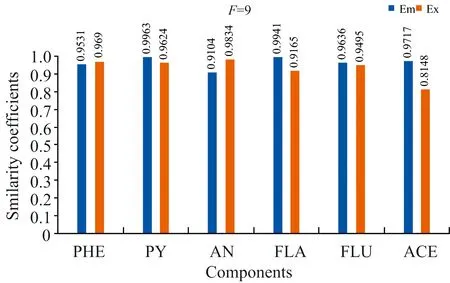
式(2)中，VT是矩阵V的转置，SN×N是一个对角矩阵，其对角元素为奇异值。利用s的s

G=USVT

(3)

奇异值分解通过分析有意义或不显著的奇异值/向量，将有价值的信号从噪声中分离出来。

2 实验和结果讨论

实验以蒽(AN)、 菲(PHE)、 芘(PY)、 芴(FLU)、 苊(ACE)和荧蒽(FLA)这六种多环芳烃(PAHs)为分析对象。不仅因为它们的光谱重叠较广，而且荧光强度差异较大。在相同浓度下，AN，PY和FLU的荧光强度相对于PHE，ACE和FLA较强，FLA为最弱的荧光发射。以去离子水为背景制备样品组，其中AN, PHE, PY, FLU, ACE和FLA的浓度分别为

2/4/6/10/3/9 μg·L-1

(X1)

7/3/1/2/5/4 μg·L-1

(X2)

1/2/3/5/7/10 μg·L-1

(X3)

8/5/2/7/1/3 μg·L-1

(X4)

3/6/9/4/10/8 μg·L-1

(X5)

9/8/7/9/3/2 μg·L-1

(X6)

以此来验证算法的有效性。

每次测试对由两个样本组成的一组样本进行带奇异值或不带奇异值的三维PARAFAC分解。通过比较PARAFAC模型的计算谱与纯组分溶液标准谱的相似程度，使用相似系数来评价谱图的分辨性能。计算得到的光谱与标准光谱之间的相似系数根据方程(4)(Tucker 1951〈A Method for Synthesis of Factor Analysis Studies〉)计算

(4)

式(4)中，x为计算得到的光谱向量，s为标准光谱向量。系数r反映了计算得到的光谱与标准光谱的相似程度。r值越大，计算谱x与标准谱s的相似度越高，通常认为相似性系数小于0.8的成分识别不成功。

首先对第一个实验数据集(X1和X2)采用直接三线性分解的三维PARAFAC分解进行拟合，根据式(1)进行初始化。在运行PARAFAC之前，需要确定组分数。所有样品都是通过在去离子水中加入6个不同比例的荧光多环芳烃制备而成。预测组分数需要大于等于添加的多环芳烃的种类数，所以选择6，7，8和9为可行的组分数。图1给出了6个分量重建的发射和激发光谱与对应的6～9个分量的标准光谱的相似系数。FLA和ACE的激发光谱(Ex)或发射光谱(Em)相似系数均小于0.80，成分数为6; PHE和FLA的相似系数低于0.80，成分数为7; FLA和ACE的相似系数低于0.80，成分数为8; FLA和ACE的相似系数低于0.80，成分数为9。

为了提高PARAFAC对两个样本光谱的分辨性能，可以再构造两个伪样本；构造伪样本的原则是，当累积贡献率首次大于99.9%时，相对应的奇异值视为强信号，而将此奇异值前的所有奇异值设为零，具体方法如下:

(1)对于每个被测样本，按照式(2)计算奇异值;

(2)奇异值的累积贡献率计算如式(5)

R(i)=(A(1)2+…+A(i)2)/(A(1)2+…+A(N)2)

i=1，…，N

(5)

(3)为了提高微弱荧光信号的分辨率，根据式(3)重新构造新的样本，将第i奇异值设为0。

其中A(i)为第i个奇异值。N是奇异值的个数。当R(i)的幅值首次大于99.9%时，对应的第i个奇异值视为强信号。

表1 样本集X1和X2的前8个奇异值累积贡献率Table 1 The first 8 cumulative contribution rates of singular values for the first set samples X1 and X2

图2 样本集X1，X2和两个伪样本提取出的六组分(PHE/PY/AN/FLA/FLU/ACE)发射光谱/激发光谱(蓝线) 以及相应的组分数为8的标准光谱(红线)

第一个样本集的奇异值累积贡献率列于表1。将样本X1的前6个奇异值设为零，样本X2的前5个奇异值设为零，其余奇异值分别构成两个新的对角矩阵。根据式(3)重构两个伪样本。在每次测试中，将两个观察样本和两个新的伪样本一起作为PARAFAC算法的输入。图2给出组分数为8的PARAFAC双向提取的发射和激发光谱。可以看出，双向提取的发射光谱和激发光谱与相应的标准光谱吻合得很好，特别是PY，AN，FLA，FLU和ACE的发射光谱，以及PHE，PY，AN，FLU和ACE的激发光谱。计算提取的发射光谱和激发光谱与6个组分对应的标准光谱的相似系数，均在0.85以上(图3)。可见，构建新的奇异值伪样本提高了弱荧光多环芳烃组分光谱的分辨能力和微弱信号的分解与放大特性。

图3 可行组分数设置从6到9下样本集X1，X2和两个伪样本中的六种不同组分激发/发射光谱和标准光谱比对的相似系数

然后根据Eq.(1)对第二个样本集X3和X4的实验数据集进行三维PARAFAC分解拟合。图4给出了提取的6个组分的发射和激发光谱与对应的6～9个组分设置下的标准光谱的相似系数，其相似系数均小于0.80。根据Eq.(3)构造两个新的伪样本。通过设置X3的前6个奇异值和样本X4的前5个奇异值为0；将四个样品(X3, X4和两个新的伪样本)输入到PARAFAC算法和设置组分数为9。提取的发射和激发光谱与对应的标准光谱的相似系数均在0.81以上(图5)。表2为样本集X3和X4的前8个奇异值累积贡献率。

表2 样本集X3和X4的前8个奇异值累积贡献率Table 2 The first 8 cumulative contribution rates of singular values for the first set samples X3 and X4

图4 可行组分数设置从6到9下样本集X3，X4中的六种不同组分激发/发射光谱和标准光谱比对的相似系数

图5 可行组分数设置从6到9下样本集X3，X4和两个伪样本中的六种不同组分激发/发射光谱和标准光谱比对的相似系数

图6为最后一组样品X5和X6，组分数为6～9，采用三维PARAFAC分解提取的六组分PAHs的结果。PHE，FLA和ACE的相似系数均小于0.80。以同样的方式构造两个新样品通过设置样本X5的前6个和X6的前5个奇异值为0(表3)，PARAFAC的分析结果由图7中给出。提取的发射光谱和激发光谱及其对应的标准光谱的相似性系数均在0.81以上，表明PARAFAC耦合奇异值分解可以提高两个观测样品对荧光强度较弱的多环芳烃的检测能力。表3为样本集X5和X6的前8个奇异值累积贡献率。

3 结 论

为了从两个样品中识别出更多的组分，提出了一种基于SVD和三维PARAFAC的方法。通过奇异值分解对混合样品的每一个三维荧光光谱进行分析，并根据奇异值的累积贡献率构建新的伪样本来突出微弱的荧光信号。结合伪样品，采用三维PARAFAC实现了两个样品水中多环芳烃重叠荧光光谱的欠定盲分离。从两个样品中成功提取了6种(PHE/PY/AN/FLA/FLU/ACE)多环芳烃的源光谱，通过比较提取的发射/激发光谱与对应的标准光谱的相似性系数实现成分识别。解析光谱与标准发射/激发光谱的相似性均在0.80以上。本研究为促进激发发射荧光光谱技术在水体多环芳烃监测中的应用提供了潜在的科学价值。

表3 样本集X5和X6的前8个奇异值累积贡献率Table 3 The first 8 cumulative contribution rates of singular values for the first set samples X5 and X6

图6 可行组分数设置从6到9下样本集X5，X6中的六种不同组分激发/发射光谱和标准光谱比对的相似系数

图7 可行组分数设置从6到9下样本集X5，X6和两个伪样本中的六种不同组分激发/发射光谱和标准光谱比对的相似系数