基于启发式搜索的带循环模型一致性检测方法
谢 燕,燕 辉,陈晓杰,段会龙,4
(1.海南大学 生物医学工程学院,海南 海口 570100;2.海南大学 信息与通信工程学院,海南 海口 570100;3.海南省生物医学工程重点实验室,海南 海口 570100;4.浙江大学 生物医学工程与仪器科学学院,浙江 杭州 310000)
0 引言
信息时代背景下,企业各种信息系统日益庞大复杂,给业务过程管理带来了挑战。在业务执行过程中,信息系统会产生大量日志,挖掘潜在的有效信息有助于监测和改进实际业务过程[1],提升业务过程的效率。因此,过程挖掘技术逐渐兴起,成为业务过程管理领域中的研究热点。过程挖掘技术从业务过程执行期间记录的事件日志中挖掘知识,其主要研究方向包括过程发现、一致性检测和过程改进[2-4]。其中,一致性检测是将一个已知过程模型与所记录的事件日志进行比较,发现、定位和解释两者偏差,以发现存在的问题和可能的改进办法。
早期,令牌重演[5-6 ]和足迹比较[7]是一致性检测中比较经典的方法,但其会因无法准确定位而出现不一致性偏差。为解决这一问题,BOSE等[8]和ADRIANSYAH等[9]引入事件日志与过程模型之间的“对齐”(alignments)概念,用于反映事件日志中记录的事件与模型允许活动之间的匹配程度。针对无循环过程模型,一般将所有对齐中偏差(也可用“代价”)最小的称为最优对齐[10](optimal alignments)。DELEONI等[10]将对齐问题映射为一个自动规划问题,但无法准确计算出最优对齐。分治法从过程模型的工作流分解和事件序列分割两个角度考虑,通过修剪搜索空间、减少计算复杂度来提高搜索速度[11-13],但对过程模型结构、事件日志遵从性有要求严格。TAYMOURI等[14]采用遗传算法求近似最优对齐,然而受初始种群和遗传收敛的影响,该方法仅能找到几个近似的最优对齐,无法保证搜索到最优解。目前,较好的计算对齐的方法是将最优对齐转化为可用A*算法搜索的最短路径问题[15-17],可以找到最优匹配,但是很难应用于复杂的过程模型。
随着业务过程复杂性和灵活性的增加,业务过程中可能会出现许多循环执行的活动。WANG等[18]提出一种基于Petri网带循环语义的过程模型和事件日志之间的偏差检测方法,该方法先识别出模型中的循环结构,再从事件序列中找到与循环结构相对应的迭代子序列,检测迭代子序列和循环结构之间的行为偏差。然而,该方法只能分析循环部分的活动序列,不能一次性检测出整体模型偏差,而且如果循环结构中出现重复活动或过程模型存在多个循环嵌套,则将对检测造成干扰,降低识别偏差的准确性。YAN[17]提出一种穷尽展开策略来查找带循环的过程模型与事件日志的最优对齐方法,该方法穷尽搜索所有循环展开情况,搜索效率低,耗费时间长,甚至导致内存溢出。启发式搜索方法[19]用于应对状态空间爆炸问题,VANDONGEN等[20]提出一种顺序前缀对齐方法,利用整数线性规划进行迭代搜索,改进对齐的可扩展区域,然而该方法是以牺牲准确性换取性能的提升。
综上所述,针对带循环的过程模型的一致性检测方法尚存在以下局限:①在包含多个循环结构或循环嵌套的过程模型中,不能确保找到全局最优对齐;②搜索效率低下。为了解决这些问题,本文提出一种新的基于启发式搜索全局最优对齐方法,该方法的主要贡献为:①对事件序列迭代部分进行分解,用来依次检查与每个迭代部分匹配的循环结构;②以事件序列与循环展开情况的匹配程度为启发信息搜索全局最优对齐,能够达到较高的效率和准确性。
1 相关知识
本章介绍一些必要的基础知识,从开展下一步计算最优对齐方法的研究。
任何具有执行语义的过程模型均可通过生成状态空间、提取状态空间中活动与活动之间的关系,转换为一个有向图模型,也称执行空间[17]。
定义1执行空间。过程模型的执行空间是一个有向图,M=(AM,RM)描述了模型中活动与活动之间的连接关系。其中:
(1)AM为执行空间中活动的集合。
(2)RM=AM×AM为一组有向弧,表示AM中活动之间的连接关系。
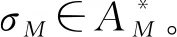
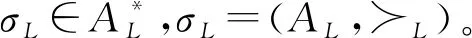
(1)AL为事件集,每个事件包括一个标识符、一个活动名称和一个时间戳。
(2)≻L=AL×AL表示对AL中的事件进行总排序,一般以时间戳排序。
事件日志L是由事件序列σL组成的有限非空集合,L=[σL1,σL2,…,σLn]。
对齐主要比较σL中的事件与M中的活动之间的相关性,反映如何在模型上重演事件序列。

(1)如果x∈AL,y=⊥,则(x,⊥)为在“事件序列上移动”,此时事件x未与执行空间中的活动匹配,对执行空间而言,x是一个额外的新增事件。
(2)如果x=⊥,y∈AM,则(⊥,y)为在“模型上移动”,此时缺少一个事件去匹配执行空间的活动y,可看作与给定执行空间相比缺失一个事件。
(3)如果在x与y相关的条件下x∈AL且y∈AM,则(x,y)为“同步移动”,表示事件x能与执行空间中的活动y匹配。
(4)其他情况为非法移动。
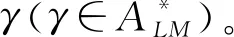
定义4最优对齐是ΓσL,M的子集,Γopt为ΓσL,M中同时满足同步移动数最大和偏差数最小的序列集合,Γopt={γopt|∀γ∈ΓσL,M[Ω(γ)<Ω(γopt)]},Ω与γ中的同步移动正相关,当两条对齐的同步移动数相同时,偏差数小的那条对齐的Ω值更大。
2 展开循环生成多个执行空间
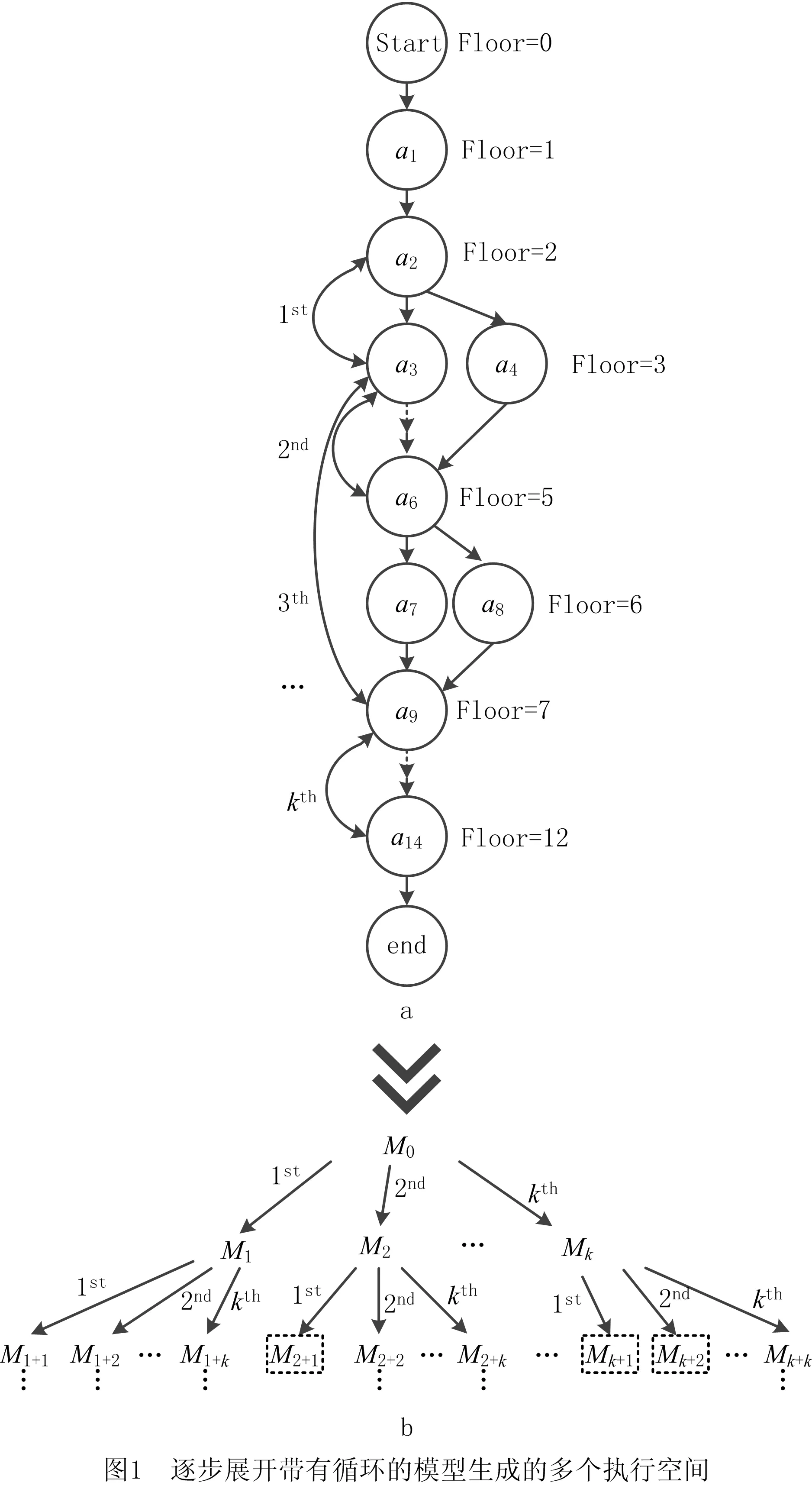
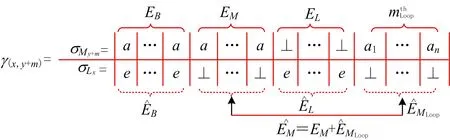
YAN[17]研究了针对不带循环的执行空间与给定事件序列的最优对齐计算方法。带循环的过程模型中可能包含多个循环结构,循环结构展开后可看作为不带循环的执行空间。由于存在多个循环结构,且每个循环结构均可被多次展开,一个带循环的过程模型所对应的无循环的执行空间数为无穷大。如图1a所示,一个带循环的执行空间MLoop中包含k个循环结构,用1st,2nd,…,kth区分循环结构出现的顺序。令M0为MLoop去掉所有循环结构的执行空间,M1,M2,…,Mk为在M0上分别展开循环1st,2nd,…,kth一次所得的执行空间。如图1b所示,从M0开始,逐渐展开循环能不断生成新的无循环的执行空间,其中每个节点表示一个执行空间,对应一种循环展开情况。例如,节点M1+2是先展开循环1st再展开循环2nd得到的执行空间。根据图1b中树结构的父—子关系,执行空间之间也可称为“父执行空间”与“子执行空间”。寻找最优对齐的关键在于能在生成的多个执行空间内找到与事件序列最匹配的执行空间。
3 事件序列分解再组合原理
在过程挖掘领域,事件序列是过程模型执行的记录(允许有偏差)。过程模型中的循环结构表示某个活动又一次被执行,对应事件序列中某个事件重复出现的情形。根据这一特点,可将事件序列按重复事件出现节点分解成若干子序列,以确定最适合被展开的循环结构。
3.1 事件序列分解
事件序列的事件名称可能与过程模型中活动的名称AM相同,YAN[17]提出执行空间中活动的Floor值的概念。Floor值表示一个活动相对Start与End的距离,例如紧跟Start的活动的Floor值为1,End前一个活动的Floor值为最长轨迹中活动的数目。图1a中标出了各活动的Floor值,延循环结构上活动的Floor值会下降。
为了检测事件序列中迭代部分,首先,为事件序列中每个事件的Mapfloor赋值。若某事件属于活动集AM,则其Mapfloor值为与该事件名称相同的活动的Floor值;若某事件不属于活动集AM,则其Mapfloor值等于零。其次,定义分解子序列的条件,即Mapfloor下降或保持不变。当Mapfloor下降时,可能存在两种情况:①Mapfloor为零,事件不能与模型中的活动配对,此时不分解子序列;②Mapfloor不为零,说明事件在其前驱事件前已发生,即重复,如果Mapfloor不变,则表示事件与其前驱事件一样,对应过程模型中一个活动的自循环。在遍历σL时,从第1个事件σL(1)开始,当检测到σL(i+1)的Mapfloor值非零且不大于σL(i)的Mapfloor值时,将从σL(1)到σL(i)的片段识别为一个子序列并存储在Segments中,σL(i+1)成为新的子序列的开端,继续检测Mapfloor值。最终,分解后所有的子序列都存储在Segments中,除Segments中的第1个子序列,其余每个子序列各表示一个迭代部分。
3.2 重新组合过程
将Segments中的子序列{Trace1,Trace2,…,Tracek+1}按下标顺序逐个取出并组合、累加,形成新的子序列集SegResult={σL0,σL1,σL2,…,σLk}。例如,σL0是Trace1,其不含迭代部分;σL1是下标为1和2的Trace组合,其相比σL0新增了一个迭代部分。这样,最后一个序列σLk就等于最初输入的事件序列σL。
4 基于启发式搜索的全局最优对齐计算方法
第3章的事件序列被转化为迭代部分递增的子序列集SegResult。为了找到与某个迭代部分最匹配的循环结构,将展开循环结构后的执行空间看作不带循环的执行空间,采用不带循环的执行空间的方法[17](又称单目标搜索空间的最优对齐计算方法)计算展开该循环结构后的局部最优对齐,当事件序列每次新增一个迭代部分时,将其局部最优对齐作为启发搜索信息,进一步找到全局最优对齐。
4.1 单目标搜索空间下的最优对齐计算方法
单目标搜索空间下的最优对齐计算方法,本质上是一个执行空间Mi与σL构成的坐标系搜索空间GMi:σL内求解最短路径的问题[17]。虽然Dijkstra算法、A*算法均能找到单目标搜索空间下的最短路径,但是A*具有更高的搜索效率。具体地,在文献[17]中,A*算法查找最短路径的代价函数为fest(n)=greal(n)+a×(hL(n)+hM(n)),其中:greal(n)表示节点n的实际代价;hM(n),hL(n)表示节点n沿模型和事件序列两个维度的预估代价;平衡因子a=0.7。
GMi:σL中的最短路径等于最优对齐的一个重要前提是合理设置GMi:σL中每条边的代价值。本文在展开循环结构时需要重新设置代价值。当节点ni扩展到下一个节点nj时,模型展开循环结构,例如图 1a 中从活动a9跳转到活动a3,在实际的坐标系上只移动了一个单位距离,代价δLoop的实际值等于1。因此,当ni扩展到nj执行循环结构时,eij的代价设置为
(1)
式中EB,EM,EL分别为沿同步维度、模型维度和事件序列维度上的边集。
4.2 展开循环前后同一事件序列的最优对齐结果比较
推论1给定一条事件序列和一个有环有向图表示的带循环的过程模型,展开循环得到的无环有向图与该事件序列的最优对齐称为子最优对齐,去掉循环的无环有向图与该事件序列的最优对齐称为父最优对齐,则子最优对齐包含的同步移动数不会小于父最优对齐中的同步移动数。
证明针对任意事件序列σLx和执行空间My,设σLx与My最优对齐表示为γ(x,y),
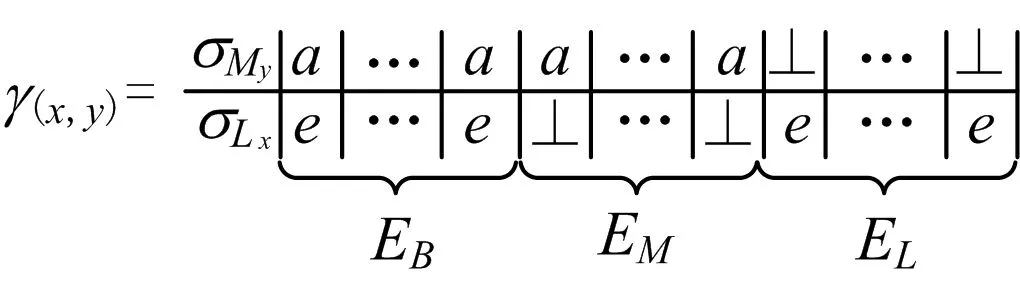
(2)
式中3种移动分别为EB,EM,EL。

(3)
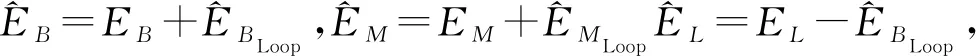
(4)

4.3 基于启发信息的全局最优对齐计算方法
利用第3章的方法,σL被分解为迭代部分递增的子序列的集合SegResult:[σL0,σL1,σL2,…,σLk]。本节依次检查σL中每个迭代部分是否能匹配模型MLoop中的循环结构,并找到与迭代部分最匹配的“有利”循环结构,逐渐确定随迭代部分递增的最优的循环结构展开过程,最终计算出全局最优对齐。
随迭代部分递增的最优循环结构展开过程如图2所示,其中:横坐标表示迭代部分递增的事件序列,纵坐标表示随循环结构展开得到的子执行空间;M0为MLoop去掉所有循环结构的执行空间,σL0为原事件序列σL分解后不包含任何迭代部分(重复事件)的子序列(见3.1节)。因此搜索的起点为(σL0,M0);坐标系中任一节点(σLx,My)表示子序列σLx与执行空间My的最优对齐结果。
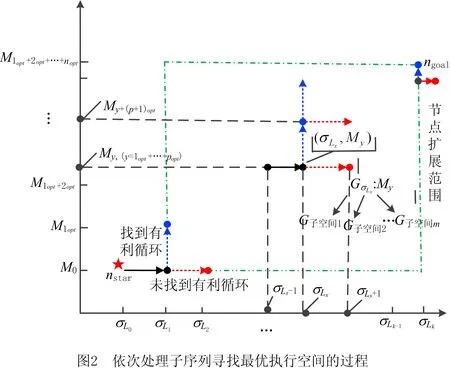
令搜索中的当前点为(σLx,My),首先确定σLx中最新加入的迭代部分是否在My处取得最好的对齐。在My上展开所有循环结构1st,2nd,…,kth一次,相应得到多个子执行空间,分别计算其与σLx之间的最优对齐。根据推论1,对于同一个事件序列σLx,在My上展开循环结构后,其子执行空间与σLx之间的最优对齐存在两种情况:
(1)同步移动数不变,但最优对齐中偏差增多 由于在My上展开了一个循环结构,即模型部分变长,同步移动数不变,表示变长的部分全部为偏差,说明σLx的最优执行空间为My,可检测下一个迭代部分,即节点(σLx,My)扩展至(σLx+1,My)(沿水平方向移动)。
(2)同步移动数增加,找到更好的最优对齐 在My上展开一个循环结构后,新的模型为My+(p+1)opt(在My上展开的第p+1个循环结构)。新模型较旧模型中间增长了一部分,增长的这部分恰好能形成同步移动,说明从My到My+(p+1)opt这一循环展开是有利的,则节点应由(σLx,My)扩展至(σLx,My+(p+1)opt)(沿垂直方向移动)。
综上所述,从起点(σL0,M0)开始,在事件序列上逐渐增加迭代部分,检查是否存在与新增迭代部分匹配的有利循环结构,利用分别沿水平方向和垂直方向扩展的启发信息逐渐确定最优的循环展开情况,直到事件序列的最后一个迭代部分检查完毕,停止搜索。启发式搜索全局最优对齐过程如算法1所示,其中Mcur为找到的执行空间,其初始值为M0,下标cur为循环结构的展开顺序,当新展开循环后得到的子执行空间比原执行空间含有更多数目的同步移动时(称为有利的循环展开情况),对Mcur进行更新。列表QLoop依次存放有利循环结构,γgoal存放每次处理子序列时找到的最优对齐。
算法1全局最优对齐算法。计算事件序列与循环模型之间的全局最优对齐。
输入:子序列集[σL0,σL1,σL2,…,σLk]、模型MLoop。
输出:记录最优循环结构展开过程列表QLoop,全局最优对齐γgoal。
1.初始化列表QLoop={};
2.初始化Mcur=M0;
3.初始化γgoal=[];
4.FOR每个子序列σLxDO //依次遍历每个子序列
5. IF σLx==σL0THEN
6. 在搜索空间G(σLx,Mcur)中寻找最优对齐,记为γ(Lx,Mcur);
7. γgoal=γ(Lx,Mcur);
8. ELSE
9. Flag=TRUE
10. DO
11. 在搜索空间G(σLx,Mcur)中寻找最优对齐,记为
γ(Lx,Mcur);
12. 将Mcur中全部有效循环结构展开1次,构建子搜索空间G(σLx,Mcur+1),G(σLx,Mcur+2),…;
13. 计算所有子搜索空间最优对齐,寻找其中最好的最优对齐记为γ(Lx,Mcur+p);
14. IF Ω(γ(Lx,Mcur))<Ω(γ(Lx,Mcur+p)) THEN //展开循环后能找到更优的对齐
15. Mcur=Mcur+P;
16. QLoop=QLoop∪{P}; //循环P是G(σLx,Mcur)最优子搜索空间中最后展开的循环结构
17. γgoal=γ(Lx,Mcur+p);
18. ELSE
19. γgoal=γ(Lx,Mcur);
20. Flag=FLASE ;
21. WHILE (Flag==TRUE)
算法1过程如下:依次从子序列集中取一个子序列σLx进行处理,找到针对子序列的最优执行空间。取第1个子序列时σLx==σL0,由于σL0中没有迭代部分,无需在Mcur上展开循环。除此之外,每个σLx相比上个子序列σLx-1新增了一个迭代部分,借助单目标最优对齐计算方法,检查在Mcur上展开1次循环后的子搜索空间中是否能找到更好的对齐,是则更新Mcur的值,令Mcur=Mcur+P,表示在Mcur上再展开有利循环结构P,将有利循环结构放入列表QLoop。Flag表示继续展开的标识符,当在子搜索空间中找不到更好的对齐时,停止对子序列σLx的处理,相当于找到了σLx的最优执行空间。遍历处理完子序列后,γgoal即存储了最后一个子序列的最优对齐,其为σL和MLoop之间的全局最优对齐。
值得注意的是,当事件序列中包含较多缺失事件时,可能出现事件序列中一个迭代部分与两个以上循环结构之间匹配的情况,需要在展开一个有利循环的执行空间My+(p+1)opt上继续展开循环结构进行查找,直到在其后代子执行空间中不能找到更优的对齐才停止对子序列σLx的搜索。
5 实例分析与计算
本章分析了一个包括4个循环结构的模型和对应事件日志集之间的偏差检测过程,验证了基于启发信息计算全局最优对齐方法的高效性和准确性。
荷兰马斯特里赫特大学医学中心ICU的机械通气脱机过程模型转换到执行空间的研究结果如图3所示,其中活动序列最大长度为11。有向图中的每个节点对应过程模型中的一个活动,节点与活动之间的映射关系如表1所示。该模型包括并行、顺序和循环结构,存在复杂循环嵌套。模型中4个循环结构按执行的先后顺序标记为1st,2nd,3rd,4th。基于启发信息计算全局最优对齐的源程序采用Python语言编写,软件环境为PyCharm2020.2.3中配置Python 3.7,硬件环境为Intel(R) Core(TM) 3.10 GHz处理器,8 GB内存。
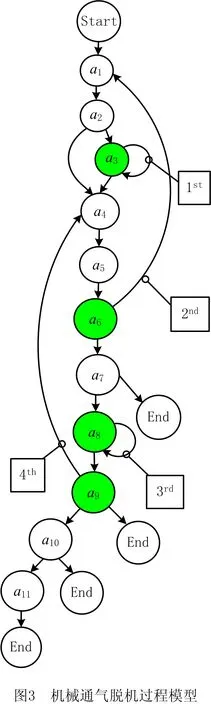

表1 图3中节点与活动之间的映射关系

续表1
检测过程中用M的下标表示循环展开情况,例如,M0表示未执行任何循环结构,M123表示循环结构执行的顺序为1st→2nd→3rd。通过随机增加或删除事件的方式在拟合的事件序列上引入偏差,将新增的事件名称均记为“Devs”。偏差率为偏差数目/对齐序列长度。
5.1 高效性
对于给定的包含多条事件序列的事件日志和执行空间,平均入队节点数指计算单条事件序列的最优对齐时生成的节点数的总和除以事件序列数,其表示勘探区域的大小;运行时间指平均检测一条事件序列的运行时间。
在查找全局最优对齐时,启发式搜索方法依赖已找到的部分循环展开结果,从迭代部分递增的子序列中寻找有利循环结构,避免检查不必要的搜索空间,具有较好的搜索效率,而文献[17]的穷尽展开策略会系统检查所有循环展开情况。将启发式搜索和穷尽展开从空间和时间复杂度进行比较,实验结果如表2所示。

表2 穷尽展开搜索和启发式搜索的比较
表2中,针对9种循环展开情况(第1列)设置了偏差率为32%左右的事件日志(L0~L8),每条日志包括100条事件序列。在相同事件序列下,当测试M0时,采用启发式搜索方法仅检查一个搜索空间GM0,σL0,而穷尽展开策略还需要检查GM0,σL0的后代子搜索空间。从测试结果可以看出,当循环结构增加时,启发式搜索方法无论在占用内存还是计算时间方面均明显优于穷尽展开策略。当模型内部循环结构数等于7时(M2212344),穷尽展开策略出现内存溢出,而启发式搜索方法的运行时间不足1 s,验证了启发式搜索方法的高效性。
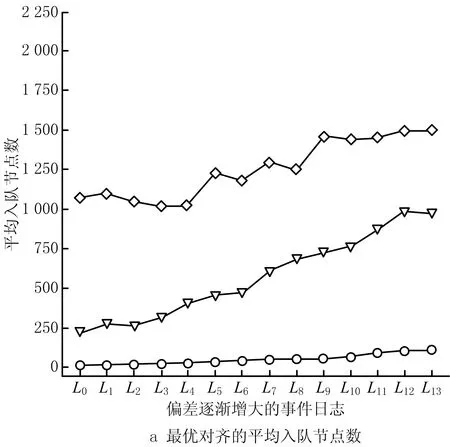
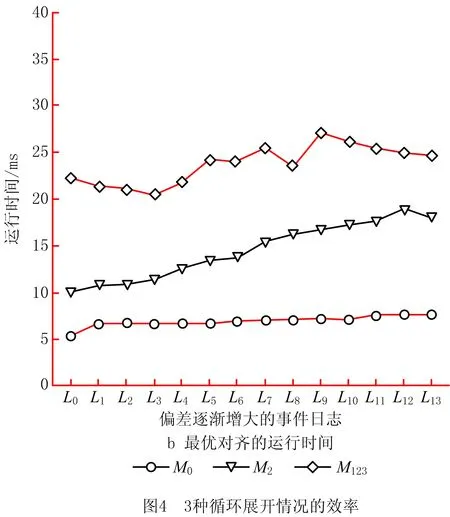
针对M0,M2,M1233种循环展开情况,设计了偏差逐渐增大的14条事件日志(L0~L13),对应平均偏差率分别为0%,10%,16%,23%,31%,35%,39%,43%,47%,51%,56%,64%,69%,75%,每条日志包括100条事件序列。图4所示为记录的平均入队节点数和运行时间,可见在偏差逐渐增大的事件日志中,最大运行时间不超过30 ms,验证了该方法的高效性。
当偏差率增大时,将在每个搜索空间探索更多节点。当随机插入缺失事件时,容易删除事件序列中的迭代部分而减少子序列数,相当于减少了搜索空间。因此,偏差逐渐增大时,平均入队节点数不完全符合递增规律。
5.2 准确性
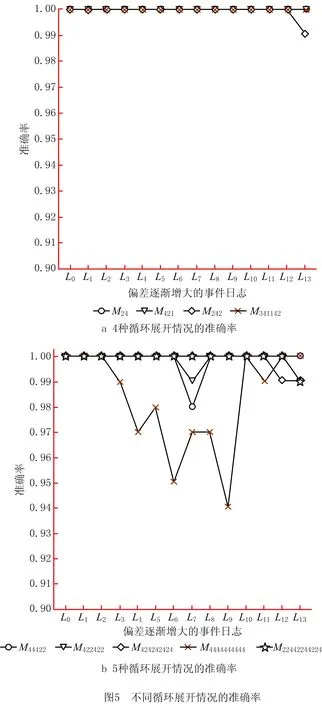
以同样方式,针对9种循环展开情况,设计了偏差率由0%增大至75%的14条事件日志(L0~L13),每条日志包括100条事件序列。图5所示为记录的准确率,其中检测到的最低准确率为94%。少部分事件序列未找到全局最优对齐,原因是:①循环2nd和循环4th两者相似度为50%(存在3个共同活动),针对个别子序列误判了最优执行空间,导致计算结果与理想的全局最优对齐之间存在较小范围的误差。在准确率最低时,实际测得的同步移动数与理想同步移动数之间的平均误差小于0.1。②在事件序列中插入过多缺失事件时,循环结构的展开部分不能与事件序列的迭代部分一一对应。针对极个别事件序列,特别是出现循环嵌套时,算法陷入局部最优。针对图4和图5中的12种循环展开情况,在偏差率逐渐增大的168条事件日志中,应用启发式策略计算全局最优对齐,测得的平均准确率为99.8%,验证了该方法的准确性。
6 结束语
针对复杂的带循环过程模型与事件序列的一致性检测问题,本文提出一种新的启发式信息搜索全局最优对齐方法。由于存在循环嵌套,不同循环结构之间相互干扰,使准确寻找全局最优对齐十分困难。为了避免陷入局部最优,首先将事件序列分解为迭代部分递增的子序列集。通过遍历处理子序列,逐渐挖掘与子序列中新增迭代部分匹配的有利循环结构,找到最优的循环结构展开过程。将已找到的有利循环结构作为启发式搜索信息,有效修剪搜索空间,提高了搜索全局最优对齐的效率。在机械通气脱机过程模型中对该方法进行仿真实验,结果表明该方法能有效解决循环模型的全局最优对齐计算问题,达到接近100%的准确率,与已有的穷尽展开策略对比显示了所提方法在效率方面的优势。
未来研究的重点是:①将该方法应用于真实事件日志,检测模型与真实事件之间的偏差,以辅助修复和增强模型;②当新增事件属于循环结构活动集时,分解后的子序列集会增大,为了匹配新增事件,将在模型中展开循环结构以检查更多的搜索空间,增加了对齐中引入的偏差数,降低了实际事件日志与模型之间的匹配程度,导致耗费过多计算时间,今后研究将结合实际考虑真实事件中迭代部分的重复概率,对事件序列进行预处理,剔除异常事件,限定循环结构展开次数,使得事件序列更接近模型的执行轨迹。

